DFS——连通性和搜索顺序(回溯)

概述

1. 定义
   在深度优先搜索中，对于最新发现的顶点，如果它还有以此为顶点而未探测到的边，就沿此边继续探测下去，当顶点v的所有边都已被探寻过后，搜索将回溯到发现顶点v有起始点的那些边。这一过程一直进行到已发现从源顶点可达的所有顶点为止。如果还存在未被发现的顶点，则选择其中一个作为源顶点，并重复上述过程。整个过程反复进行，直到所有的顶点都被发现时为止。
2. 分类
   内部dfs：一般为连通性问题，整个图作为一个状态。只需要把图中每个点都遍历到，记录其存在或者一些性质的状态即可。
   

外部dfs：一般求方案数量和最值，搜索顺序的不同状态也不同，应带有回溯。

连通性问题

模板

def dfs(u) :
	if (障碍终止条件\优化终止条件) : return ..
	if (终点终止条件) : return ..
	st[u] = True #标记已经遍历过
	for i in range(...) : #选择路径
		t = u + path[i]
		if 边界条件 : continue
		if st[t] : continue
		dfs(t)	

思考

连通性问题实质上是存在性问题，一般可以求解是否存在连通块与存在连通块的个数

迷宫

一天Extense在森林里探险的时候不小心走入了一个迷宫，迷宫可以看成是由 n∗n 的格点组成，每个格点只有2种状态，.和#，前者表示可以通行后者表示不能通行。

同时当Extense处在某个格点时，他只能移动到东南西北(或者说上下左右)四个方向之一的相邻格点上，Extense想要从点A走到点B，问在不走出迷宫的情况下能不能办到。

如果起点或者终点有一个不能通行(为#)，则看成无法办到。

注意：A、B不一定是两个不同的点。

输入格式
第1行是测试数据的组数 k，后面跟着 k 组输入。

每组测试数据的第1行是一个正整数 n，表示迷宫的规模是 n∗n 的。

接下来是一个 n∗n 的矩阵，矩阵中的元素为.或者#。

再接下来一行是 4 个整数 ha,la,hb,lb，描述 A 处在第 ha 行, 第 la 列，B 处在第 hb 行, 第 lb 列。

注意到 ha,la,hb,lb 全部是从 0 开始计数的。

输出格式
k行，每行输出对应一个输入。

能办到则输出“YES”，否则输出“NO”。

数据范围
1≤n≤100
输入样例：
2
3
.##
…#
#…
0 0 2 2
5
…
###.#
…#…
###…
…#.
0 0 4 0
输出样例:
YES
NO

import sys
sys.setrecursionlimit(110 * 110)

T = int(input())

DIRC = [[-1, 0], [0, 1], [1, 0], [0, -1]]

def dfs(sx, sy, ex, ey) :
	if g[sx][sy] == '#' :#障碍终止条件
		return False
	if sx == ex and sy == ey : return True #终点终止条件
	st[sx][sy] = True #标记状态
	for i in range(4) : #遍历路径
		a, b = sx + DIRC[i][0], sy + DIRC[i][1]
		if a < 0 or a >= n or b < 0 or b >= n : continue # 越界筛查
		if st[a][b] : continue #去重
		if dfs(a, b, ex, ey) : return True #存在通路则返回True
	return False #没有通路返回False

for t in range(T) :
	n = int(input())
	g = []
	for i in range(n) :
		g.append(input())
	sx, sy, ex, ey = map(int, input().split())
	st = [[False] * n for _ in range(n)]
	if dfs(sx, sy, ex, ey) : print("YES")
	else : print("NO")

红与黑

有一间长方形的房子，地上铺了红色、黑色两种颜色的正方形瓷砖。

你站在其中一块黑色的瓷砖上，只能向相邻（上下左右四个方向）的黑色瓷砖移动。

请写一个程序，计算你总共能够到达多少块黑色的瓷砖。

输入格式
输入包括多个数据集合。

每个数据集合的第一行是两个整数 W 和 H，分别表示 x 方向和 y 方向瓷砖的数量。

在接下来的 H 行中，每行包括 W 个字符。每个字符表示一块瓷砖的颜色，规则如下

1）‘.’：黑色的瓷砖；
2）‘#’：红色的瓷砖；
3）‘@’：黑色的瓷砖，并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。

当在一行中读入的是两个零时，表示输入结束。

输出格式
对每个数据集合，分别输出一行，显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。

数据范围
1≤W,H≤20
输入样例：
6 9
…#.
…#
…
…
…
…
…
#@…#
.#…#.
0 0
输出样例：
45

DIRC = [[-1, 0], [0, 1], [1, 0], [0, -1]]

def dfs(x, y) :
	if g[x][y] == '#' : return 0 #障碍终止条件
	
	cnt = 1 #(x, y)基点的计数
	st[x][y] = True
	for i in range(4) :
		a, b = x + DIRC[i][0], y + DIRC[i][1]
		if a < 0 or a >= n or b < 0 or b >= m : continue
		if st[a][b] : continue
		cnt += dfs(a, b)
	return cnt

while True :
	m, n = map(int, input().split())
	if m == 0 and n == 0 : break
	g = []
	for i in range(n) :
		g.append(input())
	
	st = [[False] * m for _ in range(n)]
	for i in range(n) :
		for j in range(m) :
			if g[i][j] == '@' :
				print(dfs(i, j))
				break

搜索顺序(回溯)

模板

考虑搜索顺序，就是回溯，要做到不重不漏

dfs(u) :
	if 最优性剪枝条件 : return ...
	if 终止条件 : return...
	#如果此层不会使用u则可在这里对树枝去重st[u] = True
	for i in path :
		if check(u, i) :#检查状态是否合法,可行性剪枝
			st[i] = True #树枝去重
			dfs(u + i)
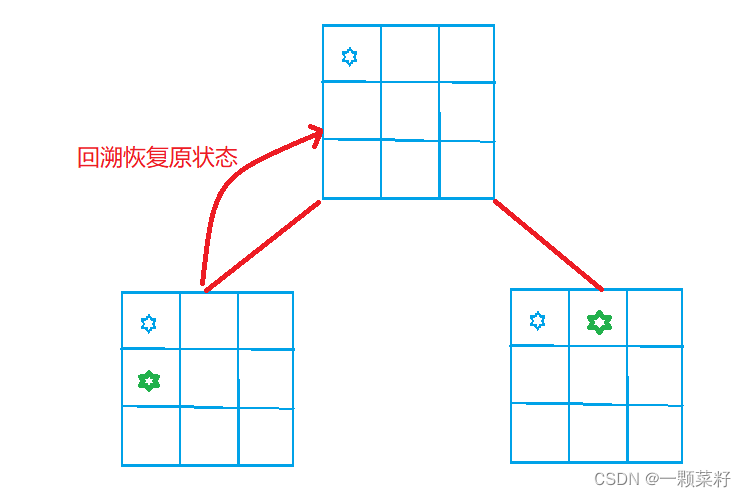
			st[i] = False #恢复现场			

思考

dfs回溯难点在于状态的保存
这里面有些技巧：
1、在回溯前预处理，首尾关系记录两两状态关系
2、对于状态的每个性质，分开存储
dfs的参数必须能够表示或者求出当前状态,这里的状态与终止条件与路径选择合法性有关
排列问题路径选择都是从头开始查找到没被遍历的节点
组合问题路径需要在上一层的基础上查找没有遍历的点

马走日

马在中国象棋以日字形规则移动。

请编写一段程序，给定 n∗m 大小的棋盘，以及马的初始位置 (x，y)，要求不能重复经过棋盘上的同一个点，计算马可以有多少途径遍历棋盘上的所有点。

输入格式
第一行为整数 T，表示测试数据组数。

每一组测试数据包含一行，为四个整数，分别为棋盘的大小以及初始位置坐标 n,m,x,y。

输出格式
每组测试数据包含一行，为一个整数，表示马能遍历棋盘的途径总数，若无法遍历棋盘上的所有点则输出 0。

数据范围
1≤T≤9,
1≤m,n≤9,
1≤n×m≤28,
0≤x≤n−1,
0≤y≤m−1
输入样例：
1
5 4 0 0
输出样例：
32

T = int(input())
DIRC = [[-2, -1], [-2, 1], [-1, 2], [1, 2], [2, 1], [2, -1], [1, -2], [-1, -2]]

def dfs(x, y, cnt) :
	global ans
	if cnt == n * m : # 终点条件
		ans += 1
		return
	st[x][y] = True
	for i in range(8) : #路径选择
		a, b = x + DIRC[i][0], y + DIRC[i][1]
		if a < 0 or a >= n or b < 0 or b >= m : continue
		if st[a][b] : continue 
		dfs(a, b)
	st[x][y] = False

for t in range(T) :
	n, m, sx, sy = map(int, input().split())
	st = [[False] * m for _ in range(n)]
	ans = 0
	dfs(sx, sy, 1)
	print(ans)

这里cnt对应于终止条件，路径选择只需要保证合法性和树枝去重即可

单词接龙

单词接龙是一个与我们经常玩的成语接龙相类似的游戏。

现在我们已知一组单词，且给定一个开头的字母，要求出以这个字母开头的最长的“龙”，每个单词最多被使用两次。

在两个单词相连时，其重合部分合为一部分，例如 beast 和 astonish ，如果接成一条龙则变为 beastonish。

我们可以任意选择重合部分的长度，但其长度必须大于等于1，且严格小于两个串的长度，例如 at 和 atide 间不能相连。

输入格式
输入的第一行为一个单独的整数 n 表示单词数，以下 n 行每行有一个单词（只含有大写或小写字母，长度不超过20），输入的最后一行为一个单个字符，表示“龙”开头的字母。

你可以假定以此字母开头的“龙”一定存在。

输出格式
只需输出以此字母开头的最长的“龙”的长度。

数据范围
n≤20，
单词随机生成。

输入样例：
5
at
touch
cheat
choose
tact
a
输出样例：
23
提示
连成的“龙”为 atoucheatactactouchoose。

N = 25

p = []
g = [[0] * N for _ in range(N)]
used = [0] * N
ans = 0

def dfs(dragon, last) : #last参数是为了判断路径选择的合法性和树枝去重
	global ans
	ans = max(ans, len(dragon))
	used[last] += 1
	for i in range(n) :
		if used[i] < 2 and g[last][i] :
			dfs(dragon + p[i][g[last][i] :], i)
	used[last] -= 1

n = int(input())
for i in range(n) :
	p.append(input())
st = input()
for i in range(n) :
	for j in range(n) :
		a, b = p[i], p[j]
		for k in range(1, min(len(a), len(b))) :
			if a[-k :] == b[:k] :
				g[i][j] = k
				break
for i in range(n) :
	if p[i][0] == st :
		dfs(p[i], i)
print(ans)

分成互质组

给定 n 个正整数，将它们分组，使得每组中任意两个数互质。

至少要分成多少个组？

输入格式
第一行是一个正整数 n。

第二行是 n 个不大于10000的正整数。

输出格式
一个正整数，即最少需要的组数。

数据范围
1≤n≤10
输入样例：
6
14 20 33 117 143 175
输出样例：
3

N = 15

st = [False] * N
group = [[0] * N for _ in range(N)]
ans = N

def gcd(a, b) : #
	return a if b == 0 else gcd(b, a % b)

def check(group, gc, i) : #判断i与group数组中所有元素是否互质
	for j in range(gc) :
		if gcd(p[group[j]], p[i]) > 1 :
			return False
	return True

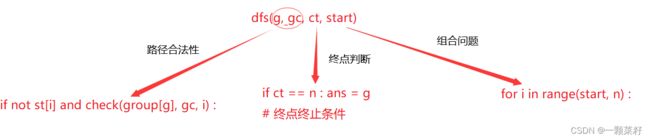
def dfs(g, gc, ct, start) :
	global ans
	if g >= ans : return # 优化剪枝
	if ct == n : ans = g # 终点终止条件
	
	flag = True #判断是否可能被划分到g组
	for i in range(start, n) :
		if not st[i] and check(group[g], gc, i) :
			st[i] = True
			group[g][gc] = i
			dfs(g, gc + 1, ct + 1, i + 1)
			group[g][gc] = 0
			st[i] = False
			flag = False
	if flag : dfs(g + 1, 0, ct, 0) #开一个新组
	
n = int(input())
p = list(map(int, input().split()))
dfs(1, 0, 0, 0)
print(ans)

总结

dfs分为连通（内部）dfs和回溯（外部）dfs，回溯dfs的枚举又分为枚举排列和组合类型的问题。