代码解读笔记整理--ConvNext：A ConvNet for the 2020s

四、ConvNext代码

1、大体框架介绍

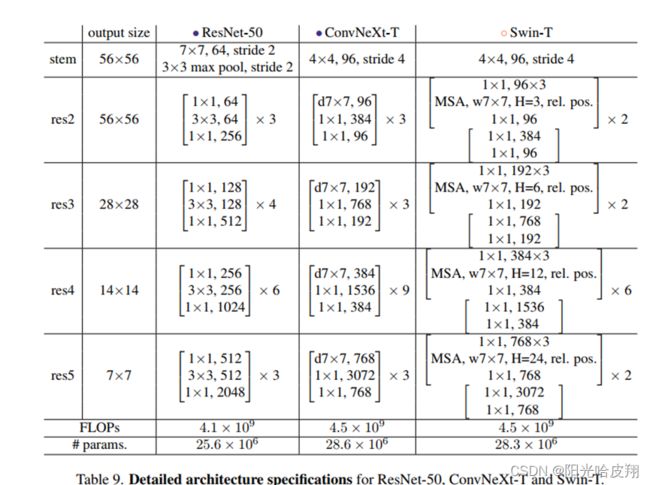
以ConvNext-Tiny为例：

其中，ConvNext包括：

（1）最底层的Stem层：对原始的图像进行预处理。

（2）四个Stage：每个Stage重复若干block，其中重复的次数为深度。

例如：第一个Stage重复了3个block，即深度为3。

（3）分类的代码：对特征进行下采样/池化，然后映射到我们要做分类的类别上。

2、代码解释

代码解释：

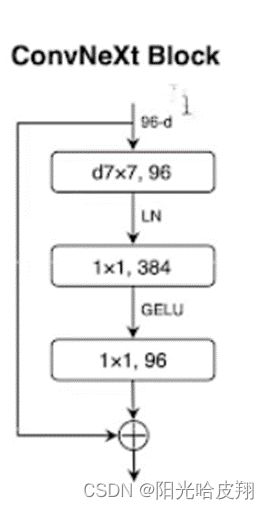
1）第一层为群卷积Group_Conv：设置group_nums=input_channels，其卷积为7x7 输出通道数为96。

2）第二层为1X1的卷积：做通道融合，也可称作一个MLP，即把上一个张量96，映射为384。不考虑周围像素点，只对单个像素点进行考虑，即不考虑空间的局部关联性。

3）第三层为1X1的卷积：即将384映射为96。

4）LN：Layer-Normalization：层归一化。

5）GELU：激活函数。

6）输入输出相结合。

（1）定义Block类：

Class Block(nn.Module):  #无论是多大的模块，都需要继承自nn.Module;

（2）定义Class Block类中的init函数：

实例化一些层。

def __init__(self, dim, drop_path=0., layer_scale_init_value=1e-6):

    super().__init__()

    self.dwconv = nn.Conv2d(dim, dim, kernel_size=7, padding=3, groups=dim) # 实例化二维卷积--depthwise conv（深度可分离卷积），设置groups等于输入通道数

    self.norm = LayerNorm(dim, eps=1e-6) #在通道上做层归一化。在做层归一化之前，张量=batchsize x H x W x channels，将张量送至层归一化中，得出均值及方差，其大小为batchsize x H x W，每个均值和方差的向量的大小为通道数目。有了均值和方差便可以进行归一化至正态分布，再引用两个仿射变换参数（权重和偏置），再变换至新的分布。

    self.pwconv1 = nn.Linear(dim, 4 * dim) # 利用linear layers 实现1x1 convs（point-wise）  ，实现放大4倍

    self.act = nn.GELU() #Gelu激活函数

    self.pwconv2 = nn.Linear(4 * dim, dim) # 利用linear layers 实现1x1 convs（point-wise）  实现缩小四倍



    self.gamma = nn.Parameter(layer_scale_init_value * torch.ones((dim)), requires_grad=True) if layer_scale_init_value > 0 else None

    self.drop_path = DropPath(drop_path) if drop_path > 0. else nn.Identity()

（3）定义Class Block类中的forward函数：

在forward函数中，将上述init所实例化的块，进行串连。

def forward(self, x):

    input = x # 输入为X

    x = self.dwconv(x) # X进入depthwise conv中，得到新的X

    x = x.permute(0, 2, 3, 1) # (N, C, H, W) -> (N, H, W, C)，X进行转置。此处的permute可进行多个维度的转置。而transpose只能进行两个维度。将C放到最后，便于后面的操作。

    x = self.norm(x) # X进行层归一化

    x = self.pwconv1(x) # X进行第一层MLP，维度放大4倍

    x = self.act(x) # X进行GELU激活

    x = self.pwconv2(x) # X进行第二层MLP，维度缩小4倍

    if self.gamma is not None:

        x = self.gamma * x 

    x = x.permute(0, 3, 1, 2) # (N, H, W, C) -> (N, C, H, W) ，转置回来

    x = input + self.drop_path(x) # X进行残差连接，即输入和输出相连

    return x

（4）定义完整ConvNext类：

class ConvNeXt(nn.Module):

（5）定义完整ConvNext类中的init函数：

def __init__(self, in_chans=3, num_classes=1000, 

             depths=[3, 3, 9, 3], dims=[96, 192, 384, 768], drop_path_rate=0., 

             layer_scale_init_value=1e-6, head_init_scale=1.,

             out_indices=[0, 1, 2, 3]

             ):

    super().__init__()

    self.dims = dims



    self.downsample_layers = nn.ModuleList() # stem and 3 intermediate downsampling conv layers

    stem = nn.Sequential(#实例化Stem，包括二维卷积和LN，放至容器Sequential

        nn.Conv2d(in_chans, dims[0], kernel_size=4, stride=4),

        LayerNorm(dims[0], eps=1e-6, data_format="channels_first")

    )

    self.downsample_layers.append(stem)

    for i in range(3):

        downsample_layer = nn.Sequential(

                LayerNorm(dims[i], eps=1e-6, data_format="channels_first"),  #下采样之前，有一个LN

                nn.Conv2d(dims[i], dims[i+1], kernel_size=2, stride=2),

        ) # kernel_size=2, stride=2。类似于Swin Transformer的patch Merging

        self.downsample_layers.append(downsample_layer)

    self.stages = nn.ModuleList() # 4 feature resolution stages, each consisting of multiple residual blocks

    dp_rates=[x.item() for x in torch.linspace(0, drop_path_rate, sum(depths))] # torch.linspace做线性划分

    cur = 0

    for i in range(4): # 4个block/stage循环

        stage = nn.Sequential(

            *[Block(dim=dims[i], drop_path=dp_rates[cur + j], 

            layer_scale_init_value=layer_scale_init_value) for j in range(depths[i])   # 每个Stage的深度进行循环]

        )

        self.stages.append(stage)

        cur += depths[i] # 记录当前总深度

self.norm = nn.LayerNorm(dims[-1], eps=1e-6) # final norm layer，分类之前最后的LN

self.head = nn.Linear(dims[-1], num_classes) # 分类层，将维度映射至类

self.apply(self._init_weights)

self.head.weight.data.mul_(head_init_scale)

self.head.bias.data.mul_(head_init_scale)

（6）定义完整ConvNext类中的init_weights函数：

def _init_weights(self, m):

    if isinstance(m, (nn.Conv2d, nn.Linear)):

        trunc_normal_(m.weight, std=.02)

        nn.init.constant_(m.bias, 0)

（7）定义完整ConvNext类中的forward_features函数：

def forward_features(self, x):

    for i in range(4):

        x = self.downsample_layers[i](x) # 共有4层下采样，包括每个block之前，以及Stem

        x = self.stages[i](x) # 下采样过后，进入到每个stage

        return self.norm(x.mean([-2, -1])) # global average pooling, (N, C, H, W) -> (N, C)，进行平均池化，将维度的高度和宽度进行平均池化，得到二维张量。

（8）定义完整ConvNext类中的forward函数：

def forward(self, x):

x = self.forward_features(x)

   x = self.head(x) # 进入MLP，batchsize映射到1000（imageNet-1k的1000个类别）。

return x