MDP模型之Grid World(值迭代方法)
近期在学习人工智能课程的时候接触到了强化学习(Reinforcement Learning),并介绍到了一种叫做MDP(马尔可夫决策)的思想,最终布置了伯克利大学的Grid World作为作业(这段话套的好深…)由于对于这个算法是真的苦手,我借鉴了YouTube的视频以及github上的代码才对该算法有了理解。在这里对我所有遇到的疑问进行记录并解答,希望也能帮到有相似问题的人。
另一篇博文:基于Q Learning的Grid World也已经整理好了,在https://blog.csdn.net/weixin_42763696/article/details/105539737可以看到。
目录
-
-
- 1 啥是Gird World
-
- 基本定义
- 术语介绍
- 不稳定智能体
- 2 在Grid World中使用值迭代
-
-
- 步骤1 得到所有action的列表
- 步骤2 计算每个action能获得的奖励之和
- 步骤3 计算出当前格子的最优方向选择
- 值迭代公式
-
- 3 参考资料
-
1 啥是Gird World
Grid World描述的是一个以格子构成的世界,如下图所示:

基本定义
其中智能体在位于Start的地方,黑色的格子表示不能走的障碍,右上角的+1,-1表示的是格子世界的终点,我们只要走到这里就算完成了目标(AI生圆满)。当然,从分数我们可以看到,+1的部分表示的是“奖励”,而-1的部分表示的是“惩罚”。
这里需要介绍一下强化学习的过程,强化学习可以看做是“摸黑探索”,在第一次从Start出发的时候,智能体完全不知道如何才能到达“奖励”的位置,可能一脚就踏入了惩罚。但经过一次又一次的尝试走向终点,他就会发现有些路会通向惩罚,不能走,并逐渐找到Reward最大的路径。
术语介绍
接下来引入几个相关的术语,以及他们在Grid World中的体现:
- State:状态,即智能体在Grid World的哪个格子
- Action:行为,即智能体会朝上下左右(东南西北)的格子移动
- Reward:奖励值(不同于终点的+1那个奖励),即智能体在当前State下能
- GAMMA:奖励折扣。越远的节点影响越小。
由于是马尔科夫模型,因此是越靠近当前节点的值对其影响越大,越远的影响越小。比如GAMMA是0.9,相邻节点值的影响就是 v a l u e 1 ∗ 0.9 value_1*0.9 value1∗0.9,再远一点的就是 v a l u e 2 ∗ 0.9 ∗ 0.9 value_2*0.9*0.9 value2∗0.9∗0.9…以此类推。
不稳定智能体
这里需要注意一点的是,智能体的行为不总是按照计划走的,当发出向上走的指令时,他只有80%的可能会正确执行(假酒害人),向左或者向右走的概率各占10%。同样,发出向右走的指令时,也会各有10%的几率向上或者向下走,如下图所示

为什么要有一个不听话的智能体?实际上,如果智能体严格按照规定来的话,那就和普通的搜索问题一样了,可以DFS或者BFS一下就能得到答案,但这是在我们知道全部信息的基础上才能实现的,假如出口无法用单纯的搜索发现,只有在你的智能体移动到出口那个位置,才知道这里是出口,该怎么办呢?对于同样规则的陷阱,又怎么能避免不踩呢?当我们掌握的信息很少的时候,做出抉择就只能依靠概率。这也就是值迭代的的目的,即通过不断的学习,最终迭代出在当前State下,执行哪个Action能更高概率的获得奖励。
2 在Grid World中使用值迭代
让我们模拟一下值迭代的过程,来理解到底发生了什么:
为了方便描述格子的坐标,以左下角为(0,0),右上角为(3,2)
初次迭代的时候我们只是知道了起点和终点的值,并没有获得更多的信息。
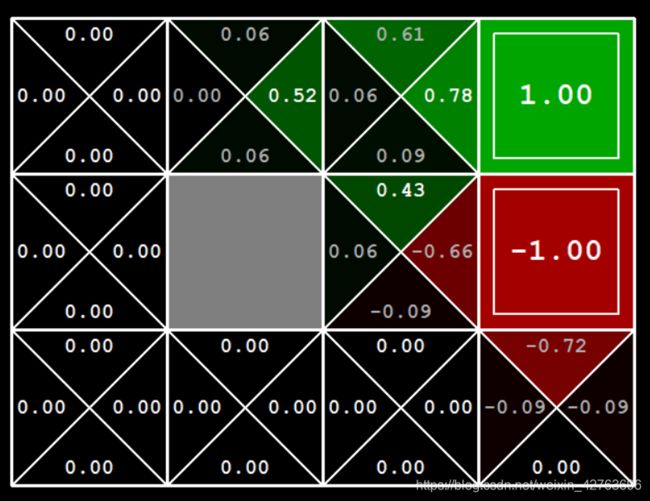
第二次迭代我们计算好多个值,让我们以坐标(2,2)处的格子为例,在该格子处的计算可以分为三个步骤:
步骤1 得到所有action的列表
在此处是[上,下,左,右]四个方向
步骤2 计算每个action能获得的奖励之和
这是比较迷惑的一点,来展开讲一下:
在(2,2)格子处,有上下左右四个方向可以走,分别分析:
上
- 80%的几率原地踏步, v a l u e 上 = 0.8 ∗ 0 value_上=0.8*0 value上=0.8∗0
- 10%的几率向左走, v a l u e 左 = 0.1 ∗ 0 value_左=0.1*0 value左=0.1∗0
- 10%的几率向右走,此时可以看到右边是有值为+1的奖励的,因此 v a l u e 右 = 0.1 ∗ 1 value_右=0.1*1 value右=0.1∗1
最终将上述求和,乘上GAMMA(见术语介绍),可以得到
r e w a r d 上 = G A M M A ∗ ( v a l u e 上 + v a l u e 左 + v a l u e 右 ) = 0.9 ∗ ( 0 + 0 + 0.1 ) = 0.09 reward_上=GAMMA*(value_上+value_左+value_右)=0.9*(0+0+0.1) = 0.09 reward上=GAMMA∗(value上+value左+value右)=0.9∗(0+0+0.1)=0.09
下 - 80%的几率下去, v a l u e 下 = 0.8 ∗ 0 value_下=0.8*0 value下=0.8∗0
- 10%的几率向左走, v a l u e 左 = 0.1 ∗ 0 value_左=0.1*0 value左=0.1∗0
- 10%的几率向右走, v a l u e 右 = 0.1 ∗ 1 value_右=0.1*1 value右=0.1∗1
r e w a r d 下 = G A M M A ∗ ( v a l u e 下 + v a l u e 左 + v a l u e 右 ) = 0.9 ∗ ( 0 + 0 + 0.1 ) = 0.09 reward_下=GAMMA*(value_下+value_左+value_右)=0.9*(0+0+0.1) = 0.09 reward下=GAMMA∗(value下+value左+value右)=0.9∗(0+0+0.1)=0.09
左 - 80%的几率向左, v a l u e 左 = 0.8 ∗ 0 value_左=0.8*0 value左=0.8∗0
- 10%的几率向上走, v a l u e 上 = 0.1 ∗ 0 value_上=0.1*0 value上=0.1∗0
- 10%的几率向下走, v a l u e 下 = 0.1 ∗ 0 value_下=0.1*0 value下=0.1∗0
r e w a r d 左 = G A M M A ∗ ( v a l u e 左 + v a l u e 上 + v a l u e 下 ) = 0.9 ∗ ( 0 + 0 + 0 ) = 0 reward_左=GAMMA*(value_左+value_上+value_下)=0.9*(0+0+0) = 0 reward左=GAMMA∗(value左+value上+value下)=0.9∗(0+0+0)=0
右 - 80%的几率向右, v a l u e 左 = 0.8 ∗ 1 value_左=0.8*1 value左=0.8∗1
- 10%的几率向上走, v a l u e 上 = 0.1 ∗ 0 value_上=0.1*0 value上=0.1∗0
- 10%的几率向下走, v a l u e 下 = 0.1 ∗ 0 value_下=0.1*0 value下=0.1∗0
r e w a r d 右 = G A M M A ∗ ( v a l u e 右 + v a l u e 上 + v a l u e 下 ) = 0.9 ∗ ( 0.8 + 0 + 0 ) = 0.72 reward_右=GAMMA*(value_右+value_上+value_下)=0.9*(0.8+0+0) = 0.72 reward右=GAMMA∗(value右+value上+value下)=0.9∗(0.8+0+0)=0.72
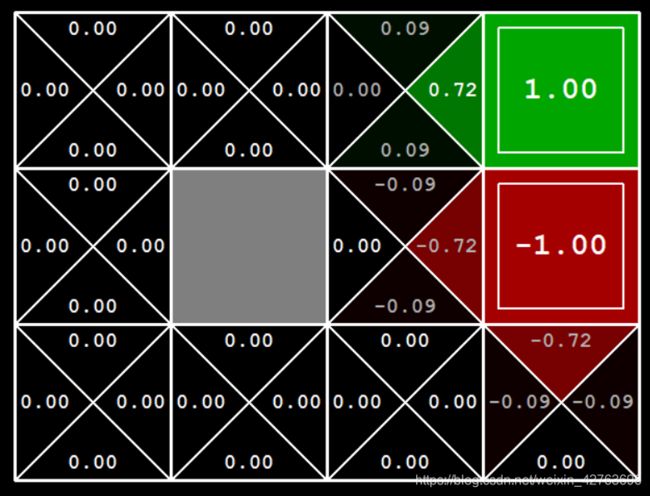
上述的计算结果都可以在图4中(2,2)位置找到。
同理,-1周围的两个格子(2,1),(3,0)也可以这样计算,计算结果如图4展示,这里就不详细展开。
最终从四个action中,保存奖励和最大的值,得图5的结果:
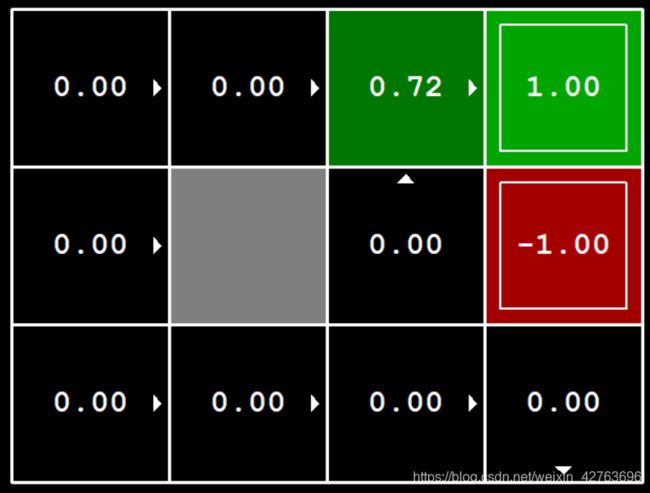
图5 保存最大奖励和
这里可以看到每个格子都有小箭头,指示的是在该格子中的最优方向选择,这是接下来要讲的步骤3。(如果没有执行步骤3的话,图5中应该只有数字结果,而没有箭头)
步骤3 计算出当前格子的最优方向选择
最优方向选择要等保存最大奖励和(即步骤2)这步执行完后再去计算。计算方法是对每个格子将步骤1,2各执行一次,由于每个格子的奖励已经更新(第一次执行的时候只有(3,2)处的+1,(3,1)处的-1这两个格子有奖励值,现在(2,2)处也有奖励值0.72了),因此执行的结果会和图4不同。
以(2,1)为例,再一次计算四个方向的奖励和:
上
- 80%的几率向上, v a l u e 上 = 0.8 ∗ 0.72 value_上=0.8*0.72 value上=0.8∗0.72
- 10%的几率向左撞墙踏步, v a l u e 左 = 0.1 ∗ 0 value_左=0.1*0 value左=0.1∗0
- 10%的几率向右走, v a l u e 右 = 0.1 ∗ − 1 value_右=0.1*-1 value右=0.1∗−1
r e w a r d 上 = G A M M A ∗ ( v a l u e 上 + v a l u e 左 + v a l u e 右 ) = 0.9 ∗ ( 0.567 + 0 − 0.1 ) = 0.428 reward_上=GAMMA*(value_上+value_左+value_右)=0.9*(0.567+0-0.1) = 0.428 reward上=GAMMA∗(value上+value左+value右)=0.9∗(0.567+0−0.1)=0.428
下 - 80%的几率下去, v a l u e 下 = 0.8 ∗ 0 value_下=0.8*0 value下=0.8∗0
- 10%的几率向左撞墙踏步, v a l u e 左 = 0.1 ∗ 0 value_左=0.1*0 value左=0.1∗0
- 10%的几率向右走, v a l u e 右 = 0.1 ∗ − 1 value_右=0.1*-1 value右=0.1∗−1
r e w a r d 下 = G A M M A ∗ ( v a l u e 下 + v a l u e 左 + v a l u e 右 ) = 0.9 ∗ ( 0 + 0 − 0.1 ) = − 0.09 reward_下=GAMMA*(value_下+value_左+value_右)=0.9*(0+0-0.1) = -0.09 reward下=GAMMA∗(value下+value左+value右)=0.9∗(0+0−0.1)=−0.09
左 - 80%的几率向左撞墙踏步, v a l u e 左 = 0.8 ∗ 0 value_左=0.8*0 value左=0.8∗0
- 10%的几率向上走, v a l u e 上 = 0.1 ∗ 0.72 value_上=0.1*0.72 value上=0.1∗0.72
- 10%的几率向下走, v a l u e 下 = 0.1 ∗ 0 value_下=0.1*0 value下=0.1∗0
r e w a r d 左 = G A M M A ∗ ( v a l u e 左 + v a l u e 上 + v a l u e 下 ) = 0.9 ∗ ( 0 + 0.072 + 0 ) = 0.0648 reward_左=GAMMA*(value_左+value_上+value_下)=0.9*(0+0.072+0) = 0.0648 reward左=GAMMA∗(value左+value上+value下)=0.9∗(0+0.072+0)=0.0648
右 - 80%的几率向右, v a l u e 左 = 0.8 ∗ − 1 value_左=0.8*-1 value左=0.8∗−1
- 10%的几率向上走, v a l u e 上 = 0.1 ∗ 0.72 value_上=0.1*0.72 value上=0.1∗0.72
- 10%的几率向下走, v a l u e 下 = 0.1 ∗ 0 value_下=0.1*0 value下=0.1∗0
r e w a r d 右 = G A M M A ∗ ( v a l u e 右 + v a l u e 上 + v a l u e 下 ) = 0.9 ∗ ( − 0.8 + 0.072 + 0 ) = − 0.655 reward_右=GAMMA*(value_右+value_上+value_下)=0.9*(-0.8+0.072+0) = -0.655 reward右=GAMMA∗(value右+value上+value下)=0.9∗(−0.8+0.072+0)=−0.655
对比 r e w a r d 上 , r e w a r d 下 , r e w a r d 左 , r e w a r d 右 reward_上,reward_下,reward_左,reward_右 reward上,reward下,reward左,reward右,可以看到 r e w a r d 上 reward_上 reward上的值最高,因此箭头冲上。
实际上我们可以看到,执行3过程的时候实际上就是又进行了一次迭代,我们可以看第三次迭代的结果图
可以看到在(2,1)处的第三次迭代结果,与步骤3中计算的结果相同。
整个迭代的过程就是遍历每个格子,并对每个格子执行步骤1,2,3,下一次迭代的时候再遍历所有的格子。知道这个以后,我们就可以手撕值迭代的公式了。
值迭代公式
值迭代的公式如下:
V i + 1 ( s ) = m a x a ∑ s ′ T ( s , a , s ′ ) [ R ( s , a , s ′ ) + γ V i ( s ′ ) ] V_{i+1}(s) = \mathop{max}\limits_{a}\sum\nolimits_{s'}T(s,a,s')[R(s,a,s')+\gamma Vi(s')] Vi+1(s)=amax∑s′T(s,a,s′)[R(s,a,s′)+γVi(s′)]
其中:
- T ( s , a , s ′ ) T(s,a,s') T(s,a,s′)表示从状态s,执行动作a后,到s’的概率。(也就是上文的80%,10%那些概率)
- R ( s , a , s ′ ) + γ V i ( s ′ ) R(s,a,s')+\gamma Vi(s') R(s,a,s′)+γVi(s′)表示到达s’后能获得的奖励值。 R ( s , a , s ′ ) R(s,a,s') R(s,a,s′)表示的是每走一步的奖励值,在上面的例子中该奖励为0; γ V i ( s ′ ) \gamma Vi(s') γVi(s′)就是用GAMMA乘在s’处的奖励值,如上文中的0.72,+1,-1这些数。
- ∑ s ′ T ( s , a , s ′ ) [ R ( s , a , s ′ ) + γ V i ( s ′ ) ] \sum\nolimits_{s'}T(s,a,s')[R(s,a,s')+\gamma Vi(s')] ∑s′T(s,a,s′)[R(s,a,s′)+γVi(s′)],可以看到是对s’进行求和,即对执行每个action时所能达到的所有s’的奖励进行求和,也就是步骤2的操作.
- m a x a ∑ s ′ T ( s , a , s ′ ) [ R ( s , a , s ′ ) + γ V i ( s ′ ) ] \mathop{max}\limits_{a}\sum\nolimits_{s'}T(s,a,s')[R(s,a,s')+\gamma Vi(s')] amax∑s′T(s,a,s′)[R(s,a,s′)+γVi(s′)],可以看到是对求a的max,也就是哪个action能得到最大的奖励,也就是步骤3的操作。
以上就是在Grid World使用值迭代方法进行对抗学习的全部过程了。
(不知道文末怎么收尾,就这吧)
3 参考资料
代码(copy过来就能跑):https://github.com/erikon/reinforcement-learning/blob/master/valueIterationAgents.py
值迭代方法讲解(别问我为啥能直接打开这个链接):https://www.youtube.com/watch?v=14BfO5lMiuk&list=PLWzQK00nc192L7UMJyTmLXaHa3KcO0wBT&index=1