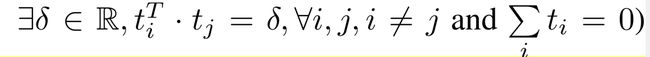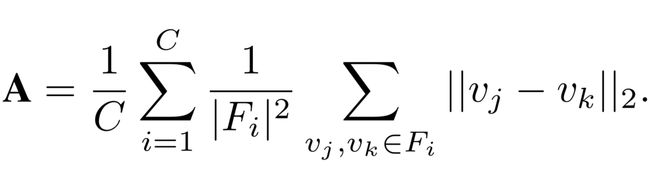Targeted Supervised Contrastive Learning for Long-Tailed Recognition(2022.5.14)
(一)解决的问题:
数据往往呈现出长尾分布,类间严重失衡,多数类可能主导训练过程,并改变少数类的决策边界。
(二)动机:
提出一种平衡采样的方法,同时能够学习到统一的特征空间,使长尾分布的数据在特征空间能够更加均匀的分布。
(三)之前的解决方法:
- 尾部类进行过采样
- 对损失函数重新加权;
缺点:这些方法过度拟合尾部类并以牺牲头部类为代价提高尾部类的性能,从而损害了学习到的特征的质量。
- 将长尾数据重新组织为组,对每个组训练一个模型,并在多特定框架中组合单个模型。
- 将表征学习与分类器学习分离可以获得良好的特征,这促使特征提取器预训练用于长尾识别(上一篇论文所提出的)
- 自监督学习并引入了k- positive contrastive learning (KCL)
KCL缺点:KCL会使学习到的特征空间的类分布均匀性差,越不平衡的类的数量会导致系统更倾向多数类的特征分布,导致少数类的学习效果不是很好。使得头类与尾类之间的距离远远大于两个尾类之间的距离。长尾数据越不平衡,特征空间的偏倚越大,分布越不均匀。
(四)步骤
- 在特征空间上确定好C个target,并确定每一个target对应的类
- 在训练时让每一个类去尽可能的靠近它对应的target
(五)Class center的确定:
解释:分子先求出Ci所对应的向量方向,在除以分母该向量的大小,得到Ci在超球上对应的向量
(六)Target的确定:
- Target之间的距离
这个公式使target的之间的距离尽量的远,且均匀分布。
- 位置的确定
一种方法是将类标签随机分配到Target位置。然而,这将导致特征空间的语义非常差。这是因为在超球体上,一些Target位置可能彼此接近,而一些则相距较远,尤其是当类数较大时(例如ImageNet和iNaturalist)。
理想情况下,语义上彼此接近的类应该被分配到彼此也很接近的Target位置。
这个公式使target的位置靠近对应类
Target确定的问题:在保持类之间的语义距离与其Target之间的欧几里德距离一致的情况下,计算匹配类与Target位置的最优分配是很困难的
解决方法:不是一开始就确定target,而是在训练过程中自适应地进行。在训练过程的每次迭代之后,使用Hungarian algorithm找出近似的最优解。
(六)训练的loss function
N是一个batch中样本的数量
vi表示xi的特征向量
˜vi表示有数据增强xi产生的特征
Vi表示一个batch中除去Xi的特征向量的其他特征向量集合(正负样本都有)
Vik+表示一个batch中Xi正样本的特征向量的集合
~Vi表示有数据增强xi产生的特征并上Vi的集合
U是一组预计算target的集合
λ为权重
损失是两个分量的和。第一种是KCL使用的标准对比损失,而第二种是target和batch样品之间的对比损失
在训练过程中,实时将Target位置分配给类,并设计有针对性的监督对比损失,让每个类的样本移动到指定的Target位置
(七)指标:
作者为了来说明一个模型在分类结果的优略,定义了如下指标
1.Intra-Class Alignment.
Fi为第i个类的特征向量集合
表示同一个类的聚集程度,越小越聚集
2.Inter-Class Uniformity.
表示类与类之间的距离。
仅仅用这两个指标的问题:不能评估一个类与其相邻类的接近程度,因为真正关心的是那些彼此太近的类,因为它们之间的决策边界可能不明确,所以将邻域一致性定义为到每个类的前k个最近的类中心的距离:
3.Neighborhood Uniformity
该公式表示类与最近的K个d类的距离大小。
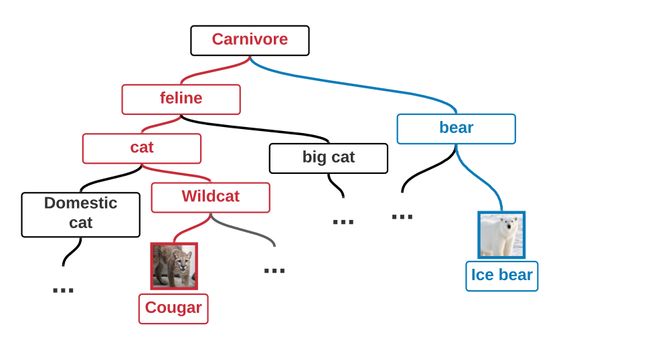
4.Reasonability.
保持合理的语义结构,即语义相近的类在特征空间中也应相近
使用WordNet层次结构计算两个类的语义距离,这是一个层次结构,其中包含所有作为叶节点的ImageNet类。然后定义两个类的语义距离为WordNet层次结构中两个叶子节点之间的最短距离
(八)消融实验:
作者指出在早期训练中,最好先对网络进行热身,不分配Target,只进行KCL损失的训练。个人理解是先让模型对类形成基本的特征空间,在进行target的定位,这样效果较好。
1.TSC与KCL及其他loss function对比
2.采样方法:
以平衡的方式抽样正样本对(如在KCL中所做的)比抽样同一类的所有样本作为正样本好(如在FCL中所做的)要好
平衡的方式抽样正样本对对TSC的提升不如对FCL的改进进步大
这可能是因为有了平衡的特征空间,每个类内的也自然平衡,因此不需要平衡的正采样策略,这进一步说明了平衡特征空间的重要性。
3.随机分配target与边训练边确定target:
两种方法对训练数据的一致性都很好。然而,产生的语义并不合理,因为语义相近的类在特征空间中并不相邻。比较了有和没有online匹配算法时TSC的合理性。没有使用online匹配算法时,TSC算法的合理性明显比有online匹配算法时差,导致泛化性能大大降低。
4.稳定性:
使用随机梯度下降(SGD)来生成最优target,因此在不同的随机种子下,所生成的Target有可能获得不同的Lu最小值,但是实验结果都趋向同一个值,说明该方法的稳定性。
(九)局限性
1.利用随机梯度下降法计算TSC的最优target,速度较快,但波动大;
2.求出超球体上能使势能最小化的点最优解仍然是一个开放问题(汤姆逊问题)。虽然TSC使用近似解决方案,也就是Hungarian algorithm来解决,这个算法只能近似去找到较优的解。
3.TSC要求预先知道类的数量,从而计算出target;因此,它不适用于类数量未知的问题