Supervised Contrastive Learning 论文学习

Abstract

在近几年，将对比学习应用在自监督表征学习上越来越受到关注，在深度图像非监督训练任务上取得了 SOTA 的性能。现在的批对比方法大幅度领先传统的对比损失，如 triplet、max-margin 和 N-pairs 损失。本文中作者将自监督批对比方法扩展至全监督任务上，使我们可以充分利用标签信息。在 embedding 空间中，属于同一个类别的点应该拉近，而不同类别的点应该推的远远的。作者分析了两种监督对比损失（SupCon），找到了最佳的损失形式。在 ImageNet 上，基于 ResNet-200，作者取得了$81.4\%$ 的 top-1 准确率，这要比该网络能取得的最高分还要高 $0.8\%$。在其它数据集和模型上，作者也取得了优异的表现。该损失函数展现了极强的鲁棒性，对于不同的超参设定（优化器和数据增广）要更加稳定。该损失函数的实现代码在：https://t.ly/supcon。

1. Introduction

交叉熵损失是监督学习下深度分类模型应用最广泛的一个损失函数。一大堆的论文都探讨了该损失的缺点，泛化性能较差。但实际上，大多数的替代方案对于较大规模的数据集都表现一般，如 ImageNet。

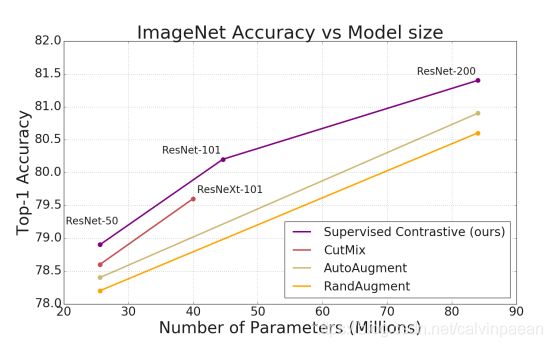
图1. SupCon 损失函数持续地领先于使用了标准数据增广的交叉熵损失。在 ImageNet 数据集上，作者列出了 ResNet-50, ResNet-101 和 ResNet-200 的 top-1 准确率，和 AutoAugment, RandAugment 和 CutMix 比较。

图2. 监督 vs. 自监督对比损失函数：对于每个 anchor，自监督对比损失（左边，等式1）会将一个正样本（即同一图片的增广版本）和有一组负样本（同一个batch里的其余样本）进行比较。而监督对比损失（右边）即等式2中的表达式，会将同类别的所有样本和该 batch 内的其余的负样本进行对比。如图片中那条黑白狗所示，在 embedding 空间中我们考虑的是同类别的标签，相同类别的元素要比自监督情形下靠的更近。

近些年，对比学习得到了重新重视，促进了自监督表征学习的发展。这些工作的一般思路就是：在 embedding 空间内，拉近 anchor 和正样本的距离，而推远 anchor 和负样本的距离。因为没有标签可用，一对正样本通常来自于对样本做数据增广，然后随机从 minibatch 中选择样本与 anchor 形成负样本对。这在图2左有描述。

本文作者基于对比全监督学习，利用标签信息，提出了一个用于监督学习的损失函数。同一类别归一化后的 embeddings 会拉近距离，而不同类别的 embeddings 会推开距离。本文技术上的创新点就是，对于每个 anchor 我们除了有许多的负样本，也会有许多的正样本（自监督对比学习中只会有一个正样本）。我们选择与 anchor 类别相同的样本作为正样本，而不是像自监督学习那样对 anchor 做数据增广。尽管我们只简单地扩展了自监督学习，但如何正确地设置损失函数并不显而易见，作者分析了两个替代方案。图2右和图1（补充）展示了该损失的内涵。该损失可以看作为 triplet 和 N-pair 损失的归纳；前者只利用了 anchor 的一个正样本和一个负样本，而后者使用了一个正样本和多个负样本。对于每个 anchor， 我们通过使用多个正负样本就可达到 SOTA 的表现，无需难例挖掘。要想把难例挖掘利用好有点困难。这是对比损失第一次在大规模分类问题上持续地领先交叉熵损失。另外，它也为自监督或监督学习提供了一个统一的损失函数。

实验显示，该损失 SupCon 实现起来很容易，训练起来比较稳定。它在 ImageNet 上取得了优异的 top-1 精度。利用 ResNet-200，它取得了 $81.4\%$的 top-1 准确率，领先最高的交叉熵损失 $0.8\%$。它不仅准确率增加了，鲁棒性也增加了。本文贡献如下：

• 提出了对比损失函数的扩展版，对于每个 anchor 使用多个正样本，将对比学习适配到全监督学习任务。
• 该损失在多个数据集上可持续提高 top-1 准确率，鲁棒性也更好。
• 分析证明该损失函数的梯度擅长从难例正负样本中学习。
• 实验证明，对于超参数的取值范围，该损失没有交叉熵损失那么敏感。

2. Related Works

本文吸收利用了自监督表征学习、度量学习和监督学习的内容。这里作者只关注在最相关的几篇论文上。交叉熵损失是一个强大的损失函数，用于训练深度网络。其核心思想简洁明了：每个类别都会有一个目标向量（1-hot）。但是人们不清楚这些目标标签为什么就应是最优的，一些论文尝试找到更优的目标标签向量。多篇论文研究了交叉熵损失的缺陷，如对错误标签、对抗样本过于敏感。人们提出了一些替代的损失函数，但它们最有效的办法就是调整标签的分布，如 label smoothing、数据增广和知识蒸馏。

基于深度学习的自监督表征学习最近在 NLP 领域取得了一些进展。在图像领域，人们利用像素预测的方法来学习 embeddings。这些方法尝试预测输入信号中缺失的部分。基于一个低维表征空间的损失，有人提出了更有效的办法来代替原先的密集、逐像素的预测损失函数。这类自监督表征学习模型都使用了对比学习方法。这些论文的损失都受到噪声对比学习或 N-pair 损失函数启发。测试时，主干网络的 embeddings 会直接用于后续的迁移任务、微调或特征提取。[15] 介绍的方法只对部分损失做反向传播，并且用 memory bank 中的表征来近似。

与对比学习相近的损失一般都基于度量距离学习或 triplets 损失函数。这些损失通常在自监督任务上进行表征学习，标签用于指导正负样本对的选取。Triplet 损失和对比损失的核心差异就是每个数据的正负样本对的数量。在每个 anchor 上，Triplet 损失只使用一个正样本和负样本。在监督度量学习任务上，我们从同类别样本中选取一对正样本，从其它类别的样本中选择一对负样本，通常需要难例挖掘来取得不错的表现。对于每个 anchor，自监督对比损失函数同样只使用一个正样本，通过 co-occurrence 或数据增广来得到。区别是对于每个 anchor 会有多对负样本。这些负样本一般是通过一些 weak knowledge 来随机选取的，比如其它图像，或随机选取视频中的某几帧，但都基于一个假设就是这些方法产生 false negatives 的概率比较低。

与本文监督对比方法相似的有 soft-nearest neighbors 损失。与[54]相似，作者通过归一化 embeddings ，以及用内积替换欧式距离的方式对[41]做了改进。作者通过数据增广、一次性对比 head 和双阶段训练（对比后进行交叉熵）的方法对[54]进一步做了优化，此外修改了损失函数的形式，显著提升了效果。[12] 使用了一个与本文损失密切相关的损失函数，通过最大化损失来纠缠中间层的表征。与本文方法最接近的是 Compact Clustering via Label Propagation(CCLP) 正则器。尽管 CCLP 主要解决半监督任务，在全监督任务上，该正则器几乎近似本文的损失形式。二者的主要区别包括作者将对比 embedding 归一到单位球面上，tuning 对比目标函数的调节参数，以及使用了更强的数据增广。此外，CCLP 将对比 embedding 作为分类head的输入，与 CCLP 正则器一起训练，而SupCon只使用了双阶段训练方式，抛弃了对比head。最后，CCLP 所进行的实验规模要远小于本文作者所进行的。对于半监督学习而言，将 CCLP 和本文的发现结合起来应该值得未来去探索。

3. Method

本文方法在结构上和自监督对比学习任务的[48,3]相近，不过是用于监督分类任务。给定一个batch的输入数据，我们首先进行两次的数据增广，得到该 batch 的两份拷贝数据。这两份拷贝数据会前向传递入一个编码器网络，得到一个 2048-维的归一化 embeddings。训练时，该表征会进一步传递入一个映射网络，推理时没有这一步。然后计算映射网络输出的监督对比损失。为了将训练好的模型用于分类，在冻结了的表征之上，作者通过交叉熵损失函数训练了一个线性分类器。

3.1 Representation Learning Framework

该框架的主要结构有：

• 数据增广模块，$Aug(\cdot )$。对于每个输入样本$x$，我们生成两个随机增广样本，$\tilde{x}=Aug(x)$，每个都代表了该数据的不同角度，包含原数据的一些子信息。第4部分会给出增广的详细内容。
• 编码器网络，$Enc(\cdot )$，将$x$映射为一个表征向量$r=Enc(x)\in {\mathbb{R}}^{D_E}$。增广后的两个样本会分别输入进该编码器，得到一对表征向量。$r$ 归一化到${\mathbb{R}}^{D_E}$的单位球面上（本文所有实验都是$D_E=2048$）。与[42,52]的发现一致，本文分析和实验证明该归一化操作能够提升 top-1 准确率。
• 映射网络，$Proj(\cdot )$，将$r$映射为一个向量$z=Proj(r)\in {\mathbb{R}}^{D_P}$。作者将$Proj(\cdot )$初始化为一个多层感知机（只有单个隐藏层，维度是 2048，输出向量大小是$D_P=128$），或只有一个大小是$D_P=128$的线性层。作者将网络的输出归一化到单位超球面上，这样就可以用内积来计算映射空间内的距离。在自监督对比学习任务[48,3]上，作者摒弃了对比训练最后的 $Proj(\cdot )$。结果就是，使用相同的编码器 $Enc(\cdot )$，本文的推理模型和交叉熵模型的参数量是一样的。

3.2 Contrastive Loss Functions

给定该框架，我们首先回顾下对比损失家族，从自监督领域开始，并分析如何将其应用到监督领域。给定由 $N$ 对随机样本/标签组成的集合，$\{x_k,y_k{\}}_{k=1,...,N}$，对应的训练 batch 就有$2N$对，$\{{\tilde{x}}_l,{\tilde{y}}_l{\}}_{l=1,...,2N}$，其中${\tilde{x}}_{2k}$和${\tilde{x}}_{2k-1}$是$x_k(k=1,...,N)$的2个随机增广样本，并且${\tilde{y}}_{2k-1}={\tilde{y}}_{2k}=y_k$。本文其余部分中，batch 指一个由$N$个样本组成的集合，$2N$个增广样本组成的集合称为 multiviewed batch。

3.2.1 Self-supervised Contrastive Loss

在一个 multiviewed batch 内，$i\in I\equiv \{1,...,2N\}$表示一个随机被增广样本的索引，$j(i)$ 是产生的增广样本的索引。在自监督对比学习中，该损失表达式为：

$${\mathcal{L}}^{self}=\sum _{i\in I}{\mathcal{L}}_i^{self}=-\sum _{i\in I}\log \frac{\exp (z_i\cdot z_{j(i)}/\tau )}{{\sum }_{a\in A(i)}\exp (z_i\cdot z_a/\tau )}$$

这里，$z_l=Proj(Enc({\tilde{x}}_l))\in {\mathcal{R}}^{D_P}$，$\cdot$符号表示内积，$\tau \in {\mathcal{R}}^{+}$ 是一个标量调节参数，$A(i)\equiv I\backslash \{i\}$。索引$i$叫做 anchor，索引$j(i)$叫做正样本，其它的$2(N-1)$索引（$\{k\in A(i)\backslash \{j(i)\}\}$）叫做负样本。

注意对于每个 anchor $i$，都有一对正样本和$2N-2$对负样本。分母总共有$2N-1$项（正样本和负样本）。

3.2.2 Supervised Contrastive Loss

对于监督学习来说，因为我们知道标签信息，等式1的对比损失就能处理同类别多于一个样本的情况。但是面对任意个数的正样本的情况，我们得在多个备选函数之间做出抉择。

$${\mathcal{L}}_{out}^{sup}=\sum _{i\in I}{\mathcal{L}}_{out,i}^{sup}=\sum _{i\in I}\frac{-1}{|P(i)|}\sum _{p\in P(i)}\log \frac{\exp (z_i\cdot z_p/\tau )}{{\sum }_{a\in A(i)}\exp (z_i\cdot z_a/\tau )}$$

$${\mathcal{L}}_{in}^{sup}=\sum _{i\in I}{\mathcal{L}}_{in,i}^{sup}=\sum _{i\in I}-\log \{\frac{1}{|P(i)|}\sum _{p\in P(i)}\frac{\exp (z_i\cdot z_p/\tau )}{{\sum }_{a\in A(i)}\exp (z_i\cdot z_a/\tau )}\}$$

这里，$P(i)\equiv \{p\in A(i):{\tilde{y}}_p={\tilde{y}}_i\}$ 是 multiviewed batch 中与 $i$ 不同所有正样本集合的索引，$|P(i)|$是该集合元素的个数。等式2中，对所有正样本的求和操作位于 $\log ({\mathcal{L}}_{out}^{sup})$ 之外，而在等式3中，求和操作位于$\log ({\mathcal{L}}_{in}^{sup})$ 之内。这两个损失函数都具有下面的特性：

• 一般化至任意个数的正样本。等式2和3的主要结构调整就是，对于任一个 anchor，multiviewed batch 中所有的正样本（即增广样本和相同标签的其余样本）都作用于分子。对于样本数大于类别数的随机产生的 batches，会出现多个额外的项（平均是 $N/C$，$C$是类别个数）。对于同一类别下的样本，监督损失促使编码器生成距离近的表征，得到一个比等式1更加鲁棒的表征空间 clusters。
• 负样本越多，对比力度越强。等式2和3都保留了等式1中的分母，对负样本求和。这受到噪声对比估计和 N-pair 损失启迪，通过增加更多的负样本来提高信噪分离的能力。通过自监督对比学习，该特性对于表征学习很重要，许多论文都证明了负样本越多，性能越好。
• 正负样本难例挖掘的天赋。当我们用归一化的表征时，等式1的损失函数能得到一个梯度结构，具备隐式的正负样本难例挖掘的能力。从正负样本难例中得到的梯度贡献（持续地与 anchor 做对比，对编码器帮助很大）要大一些，而从容易样本中得到的梯度贡献（持续地与 anchor 做对比，对编码器帮助很弱）要小一些。此外，难例正样本的作用会增长得极快。等式2和3都保留了这个有用的特性，可以一般化到所有的正样本上。这个特性使我们不再需要显式的难例挖掘。作者发现，这个特性可以用到监督和自监督对比损失，但本文是第一个清楚地展示该特性的工作。作者在补充材料中提供了该特性损失梯度的完备推导。

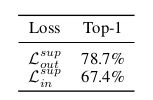
表1. 对于监督对比损失，ImageNet top-1 分类准确率，主干网络是 ResNet-50，batch size 是6144。

但是这两个损失并不等价。因为$\log$是一个凹函数，根据 Jensen 不等式可得到${\mathcal{L}}_{in}^{sup}\le {\mathcal{L}}_{out}^{sup}$。因此我们可以认为 ${\mathcal{L}}_{out}^{sup}$ 更适合（因为它是${\mathcal{L}}_{in}^{sup}$的上界）。分析数据也支持该论断。表1比较了 ImageNet top-1 分类准确率。${\mathcal{L}}_{out}^{sup}$监督损失的效果要比${\mathcal{L}}_{in}^{sup}$高不少。作者推测这是因为${\mathcal{L}}_{in}^{sup}$的组成差于${\mathcal{L}}_{out}^{sup}$的结构。对于${\mathcal{L}}_{out}^{sup}$，正样本归一化因子（即 $1/|P(i)|$）用于去除 multiviewed batch 中正样本对损失贡献的偏差。但是，尽管${\mathcal{L}}_{in}^{sup}$也包含了同样的归一化因子，它位于$\log$的里面。因此它相当于只给整体损失加了一个常数，不会影响整体的梯度。没有了归一化的影响后，${\mathcal{L}}_{in}^{sup}$的梯度就更容易受正样本中偏差的影响，造成训练模型不是最优的。

对梯度自身的分析支持这个结论。在补充材料中有说明，关于 embedding $z_i$ 的${\mathcal{L}}_{out,i}^{sup}$或${\mathcal{L}}_{in,i}^{sup}$的梯度有着如下的形式。

$$\frac{\partial {\mathcal{L}}_i^{sup}}{\partial z_i}=\frac{1}{\tau }\{\sum _{p\in P(i)}{z}_p(P_{ip}-X_{ip})+\sum _{n\in N(i)}{z}_n{P}_{in}\}$$

这里，$N(i)\equiv \{n\in A(i):{\tilde{y}}_n\ne {\tilde{y}}_i\}$ 是 multiviewed batch 中所有负样本组成的集合的索引，$P_{ix}\equiv \exp (z_i\cdot z_x/\tau )/{\sum }_{a\in A(i)}\exp (z_i\cdot z_a/\tau )$。两个损失函数的梯度区别在于 $X_{ip}$。

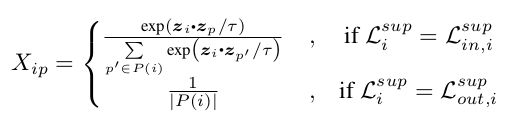
如果每个 $z_p$ 都设为正样本表征向量的平均值$\overline{z}$，$X_{ip}^{in}$ 就变成了$X_{ip}^{out}$。

$$X_{ip}^{in}{|}_{z_p=\overline{z}}=\frac{\exp (z_i\cdot \overline{z}/\tau )}{{\sum }_{p^{\prime }\in P(i)}\exp (z_i\cdot \overline{z}/\tau )}=\frac{\exp (z_i\cdot \overline{z}/\tau )}{|P(i)|\cdot \exp (z_i\cdot \overline{z}/\tau )}=\frac{1}{|P(i)|}=X_{ip}^{out}$$

从$\partial {\mathcal{L}}_i^{sup}/\partial z_i$，作者发现了其稳定的原因，使用正样本的均值有助于训练。论文的余下部分，我们只考虑${\mathcal{L}}_{out}^{sup}$。

4. Experiments

作者在常用的图像分类基准（Cifar10、Cifar100 和 ImageNet）上计算了 SupCon (${\mathcal{L}}_{out}^{sup}$)损失的分类准确率。作者也在问题图像上测试了模型的鲁棒性，展示模型的性能如何随着超参数和数据的变化而变化。编码器使用了三个常用的网络结构：ResNet-50, ResNet-101 和 ResNet-200。最后一个池化层的归一化了的激活值（$D_E=2048$）作为表征向量使用。对于 $Aug(\cdot )$ 作者尝试了四种数据增广方法：AutoAugment, RandAugment, SimAugment 和 Stacked RandAugment（补充材料中有详细介绍）。主干网络为 ResNet-50，在 SupCon 和交叉熵损失上，AutoAugment 的表现要优于其它的增广策略。Stacked RandAugment 在 ResNet-200 上的表现最好。补充材料中给出了详细说明。

4.1 Classification Accuracy

表2展示了在 CIFAR-10、CIFAR-100 和 ImageNet 上，SupCon 的泛化性要好于交叉熵、margin 分类器（使用了标签信息）和非监督对比学习技术。表3展示了 ImageNet 上 ResNet-50 和 ResNet-101 的结果。在 ResNet-50 上使用 AutoAugment，作者取得了 $78.7\%$的 SOTA 准确率。注意，相较于 CutMix，也实现了一些提升，CutMix 是目前 SOTA 的增广策略。将数据增广策略（CutMix 或 MixUp）加入对比学习可能会进一步提高表现。

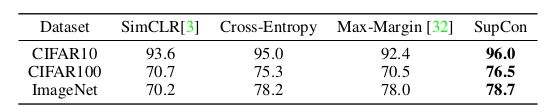
表2：在各种数据集上，ResNet-50 的 Top-1分类准确率。作者比较了交叉熵训练、非监督表征学习（SimCLR）、max-margin 分类器和SupCon。作者重新实现并调参了所有基线模型，除了 margin 分类器。注意 CIFAR-10 和 CIFAR-100 的结果是用 PyTorch 实现的，ImageNet 是用 TensorFlow 实现的。

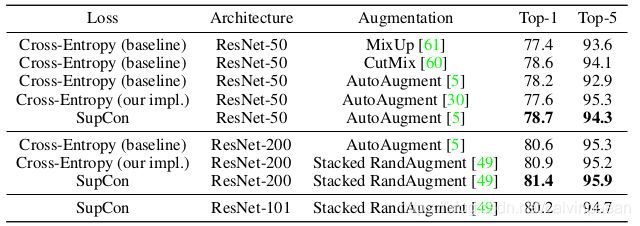
表3：对 ResNet-50 使用 AutoAugment，对 ResNet-101、ResNet-200 使用 Stacked RandAugment 的 Top-1/Top-5 的准确率结果。基线模型的数据来自于引用的论文，作者也重新实现了交叉熵损失。

在 ImageNet 上，主干网络是 ResNet-50，当内存大小是 8192（只用存储 128 维向量），batch size 是256，使用 SGD 优化器，在8张特斯拉 V100 GPUs 上训练，SupCon 取得了 $79.1\%$ 的 top-1 准确率。这比 6144 的 batch size 取得的 $78.7\%$ 的准确率只高一点；却极大地降低了计算和内存消耗。

因为对于每个样本，SupCon 会用到两个增广样本，它的 batch size 就是交叉熵损失的2倍。因此作者也试验了 ResNet-50 交叉熵基线模型，batch size 是12288。但只得到了$77.5\%$ 的 top-1 准确率。此外，作者也尝试增加训练的 epoch 数到1400，但降低了准确率（$77.0\%$）。

作者测试了 N-pairs 损失函数，batch size 为6144。N-pairs 在 ImageNet 上只取得了 $57.4\%$的 top-1 准确率。作者认为，这是因为 N-pairs 损失不具备监督对比学习的一些条件：使用多个增广样本；较弱的参数调节；更多正样本。在补充材料中，作者展示了每个 anchor 的正样本个数的影响。作者也注意到 N-pairs 原论文证明了 N-pairs 损失要优于 triplet 损失。

4.2 Robustness to Image Corruptions and Reduced Training data

DNN 对于异常数据或缺陷图像（如噪点、模糊或JPEG压缩）的鲁棒性较差。ImageNet-C 基准就是用于评价训练模型对于这些问题的表现。图3左，作者使用 Mean Corruption Error(mCE) 和 Relative Mean Corruption Error 指标比较了监督对比模型和交叉熵损失。这两个指标都评估模型的平均退化程度，对所有可能的异常问题和问题的严重级别求均值。当我们比较各模型不同的 Top-1 准确率时，Relative mCE 要更好一些，而mCE更适合评价模型面对异常情形时的绝对鲁棒性。SupCon 模型对于不同的异常问题，mCE 要更低一些，鲁棒性要更好。从图3右可以看到，当异常程度递增时，SupCon 模型的退化要更少。

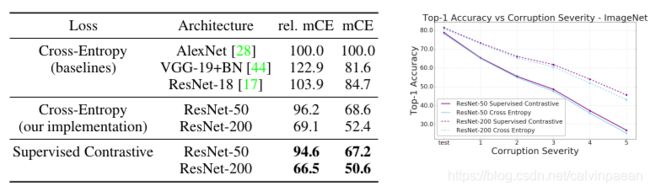
图3：使用监督对比损失训练，让模型更加鲁棒。左边：在ImageNet-C上，通过 mCE 和 Relative mCE 来评估鲁棒性（越低越好）。右边：对于不同程度的异常，平均准确率的变化（越高越好）。

4.3 Hyperparameter Stability

通过依次地改变增广策略、优化器和学习率，作者对超参数的稳定性做了试验。图4a 中，作者比较了 SupCon 损失和交叉熵损失的 top-1 准确率随着增广策略（RandAugment [6], AutoAugment [5], SimAugment [3], Stacked RandAugment [49]）、优化器(LARS, SGD with Momentum and RMSProp)和学习率的改变而改变的程度。作者观察到对比损失输出具有较低的方差。注意交叉熵损失的 batch size 和监督对比学习是一样的，因此排除了 batch size 的影响。在图4b中，只有 batch size 变动，而保留所有其它的超参数不变，监督对比损失会产生更高的 top-1 准确率。

图4：交叉熵损失和监督对比损失关于超参数和训练数据大小的准确率，都是在 ImageNet 上通过 ResNet-50 编码器计算得到。（从左到右）a: 标准的盒形图展示 Top-1 准确率 vs. 增广策略、优化器和学习率变动。(b) Batch size 变动下的 Top-1 准确率，显示 batch size 越大越好，而且监督对比的 Top-1 准确率要更高，哪怕当 batch size 较小的时候。c: 不同训练 epochs 下 SupCon 的 Top-1 准确率。(d): 不同 temperature 值下 SupCon 的 Top-1 准确率。

表4：迁移学习结果。这些值分别是在 VOC2007 上计算得来的 mAP、Aircraft, Pets, Caltech 和 Flowers 数据集上得到的类别平均准确率，以及其它数据集上的 top-1 准确率。

4.4 Transfer Learning

在12个自然图像数据集上，作者对微调得到的表征进行了评价。当使用相同的网络结构时，SupCon 能取得与交叉熵和自监督对比损失相同的迁移学习表现（见表4）。

4.5 Traning Details

针对 ResNet-200，SupCon 损失训练了700个 epochs 进行预训练，而对于其它小一些的模型训练了350个 epochs。图4c 就是对于 ResNet-50 来说，其准确率和训练 epochs 的关系，显示 200个 epochs 通常就足够了。

一个可选的步骤就是训练一个线性分类器，计算 top-1 准确率。如果我们的目的是将表征用于迁移学习或特征提取，这一步就不是必须的。第二阶段只需要10个 epochs 的额外训练。实际操作中，该线性分类器能和编码器、映射网络一起训练，将线性分类器的梯度冻结，不回传给编码器，效果是差不多的。作者为了剥离对 SupCon 损失的影响，没有用这一步。

作者使用的 batch size 是6144,尽管 2048 对于 SupCon 和交叉熵损失都足够用了（如图4b所介绍的）。作者认为一部分的性能提升得益于 batch size 对梯度的影响，因为负样本增多，难例正样本就会增多。作者在实验中报告了ResNet-50 中 batch size 为6144的情况，以及 ResNet-200 中 batch size 为4096的情况（对于较大的网络，较小的 batch size 就够用了）。作者发现，对于相同的batch size，SupCon 使用的学习率可以比交叉熵大一些，但效果是差不多的。

所有的实验中，temperature $\tau =0.1$。Temperature 越小，越有利于模型训练结果，但是太小了也不利于训练，因为数值不稳定。图4d 展示了它的影响。如等式4中所见，梯度的大小和$\tau$的值呈反比，因此出于稳定训练的目的，用$\tau$来缩放损失。

在初始的预训练和后面的训练过程中，作者用标准的优化器做实验，比如 LARS, RMSProp, SGD with momentum。SGD with momentum 对于使用交叉熵的 ResNets 来说效果最好，而在 ImageNet 上，对于 SupCon，作者使用了 LARS 进行预训练，RMSProp 来训练线性层。对于 CIFAR10 和 CIFAR100，SGD with momentum 最好。补充材料中提供了各优化器组合的效果。

5. Training Setup

在图5中，作者比较了交叉熵损失、自监督对比和 SupCon 损失的设定。注意推理模型中的参数个数保持不变。作者也注意到，没必要在第二阶段中训练一个线性分类器，而之前的工作会用到 k-Nearest Neighbor 分类等方法来计算表征，进行分类任务。线性分类器可与编码器一同训练，只是它的梯度不会反向传播回编码器。

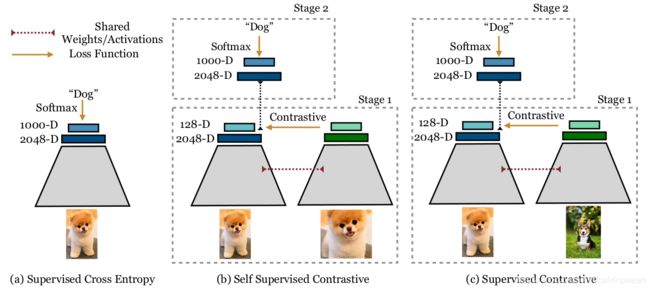
图5. 交叉熵损失、自监督对比损失和监督对比损失：交叉熵损失（左边）使用了标签和 softmax 损失来训练一个分类器；自监督对比损失（中间）使用一个对比损失和数据增广来学习表征。监督对比损失（右边）通过一个对比损失来学习表征，但除了增广图片之外，也使用了标签信息来采样正样本。这两个对比方法都有一个可选的第二阶段，即对学到的表征训练一个模型。