线性回归模型-误差分析
线性回归误差分析
- 误差分析作用
- 偏差与方差
-
- 图形定义
- 数学上是如何推导出的呢
- 出现偏差与方差误差,分别该如何处理呢
- 评估指标数值多少合适?
误差分析作用
我们在做机器学习模型的时候,训练完模型后,往往需要对模型进行性能评估,进行选择,数值预测模型的评估,有以下的常用评估指标:
- 均方误差:是最常见的指标,但是容易受到奇异值的影响
- 平均绝对误差
- 方均根差
- R平方系数
- 借助图形分析工具
其实这些线性回归的评估指标万变不离其宗都离不开二个核心的数值,偏差与方差,说白就是在评估模型的时候,如果评估指标效果理想,就要想办法降低偏差与方差的数值。
偏差与方差
这里重点解释一下偏差与方差
泛化误差可以分解成偏差的平方加上方差加上噪声。
偏差:度量了学习算法的期望预测和真实结果的偏离程度,刻画了学习算法本身的拟合能力。
方差:度量了同样大小的训练集的变动所导致的学习性能的变化,刻画了数据扰动所造成的影响,噪声表达了当前任务上任何学习算法所能达到的期望泛化误差下界,刻画了问题本身的难度。
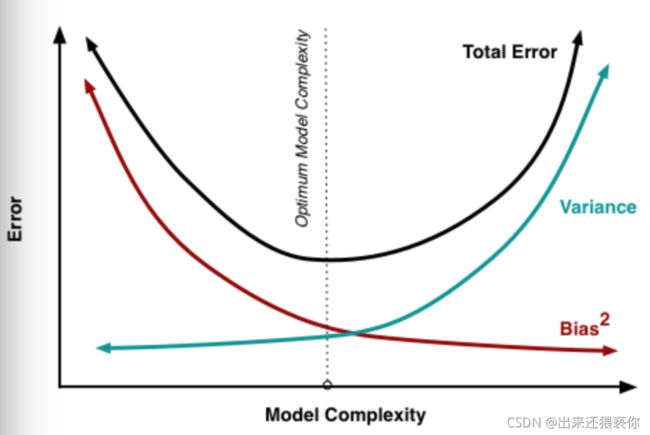
偏差和方差一般称为bias和variance,一般训练程度越强,偏差越小,方差越大,泛化误差一般在中间有一个最小值,如果偏差较大,方差较小,此时一般称为欠拟合,而偏差较小,方差较大称为过拟合。
图形定义
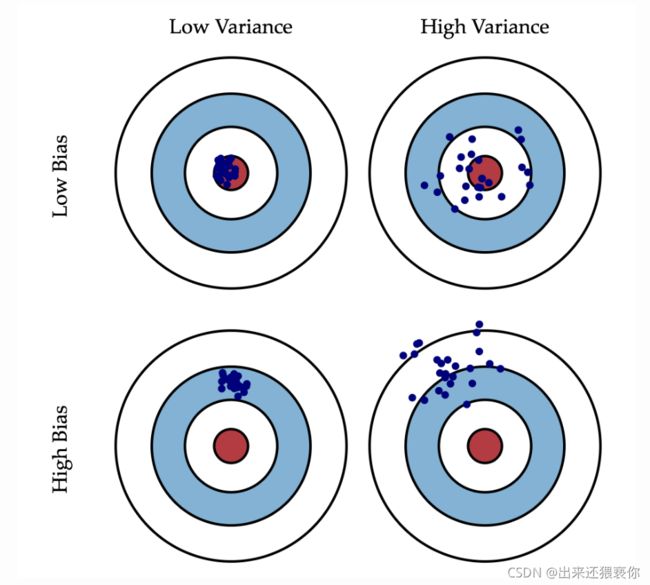
这是一张常见的靶心图。可以想象红色靶心表示为实际值,蓝色点集为预测值。在模型不断地训练迭代过程中,我们能碰到四种情况:
- 低偏差,低方差:这是训练的理想模型,此时蓝色点集基本落在靶心范围内,且数据离散程度小,基本在靶心范围内;
- 低偏差,高方差:这是深度学习面临的最大问题,过拟合了。也就是模型太贴合训练数据了,导致其泛化(或通用)能力差,若遇到测试集,则准确度下降的厉害;
- 高偏差,低方差:这往往是训练的初始阶段;
- 高偏差,高方差:这是训练最糟糕的情况,准确度差,数据的离散程度也差。
数学上是如何推导出的呢
通常我们在选择偏差与方差作为评估指标的时候,其实就是把模型的误差看成是
误 差 = 方 差 + 偏 差 2 + 噪 声 误差=方差+偏差^2+噪声 误差=方差+偏差2+噪声
数学推导如下:
我们假设有训练数据集 S = ( x i , y i ) S={(x_i,y_i)} S=(xi,yi)
令 y i = f ( x i ) + ε y_i = f(x_i) + ε yi=f(xi)+ε,为实际方程,其中ε是满足正态分布均值为0,标准差为σ的值。
假设预测方程为 h ( x ) = w x + b h(x) = wx + b h(x)=wx+b,这时我们希望总误差
E r r ( x ) = ∑ i = 0 n ( y i − h ( x i ) ) 2 Err(x) = \sum_{i=0}^n(y_i - h(x_i))^2 Err(x)=∑i=0n(yi−h(xi))2 能达到最小值,这里可以把这个问题理解为求期望 E [ y i − h ( x i ) ] 2 E[y_i - h(x_i)]^2 E[yi−h(xi)]2最小值
求解 E r r ( x ) Err(x) Err(x):
E [ y − h ( x ) ] 2 = E [ y 2 − 2 y h ( x ) + h ( x ) 2 ] E [y - h(x)]^2 = E [y2 - 2yh(x) + h(x)^2] E[y−h(x)]2=E[y2−2yh(x)+h(x)2]
= E [ y 2 ] − 2 E [ y ] E [ h ( x ) ] + E [ h ( x ) 2 ] = E [y2] - 2E[y] E[h(x)] + E[h(x)2] =E[y2]−2E[y]E[h(x)]+E[h(x)2]
= E [ ( y − y ) 2 ] + y 2 − 2 E [ y ] h ( x ) + E [ ( h ( x ) − h ( x ) ) 2 ] + h ( x ) 2 = E [(y - y)^2] + y^2 - 2E[y]h(x) + E [(h(x) - h(x))^2] + h(x)^2 =E[(y−y)2]+y2−2E[y]h(x)+E[(h(x)−h(x))2]+h(x)2
= E [ ( y − ( f x ) ) 2 ] + f ( x ) 2 − 2 f ( x ) h ( x ) + E [ ( h ( x ) − h ( x ) ) 2 ] + h ( x ) 2 = E [(y - (fx))^2] + f(x)^2 - 2f(x)h(x) + E [(h(x) - h(x))^2] + h(x)^2 =E[(y−(fx))2]+f(x)2−2f(x)h(x)+E[(h(x)−h(x))2]+h(x)2
= E [ ( h ( x ) − h ( x ) ) 2 ] + ( h ( x ) − f ( x ) ) 2 + E [ ( y − ( f x ) ) 2 ] = E [(h(x) - h(x))^2] + (h(x) - f(x))^2 + E[(y - (fx))^2] =E[(h(x)−h(x))2]+(h(x)−f(x))2+E[(y−(fx))2]
= v a r i a n c e + b i a s 2 + n o i s e = variance + bias^2 + noise =variance+bias2+noise
一般来说,随着模型复杂度的增加,方差会逐渐增大,偏差会逐渐减小。
出现偏差与方差误差,分别该如何处理呢
低偏差,高方差:
- 增加训练样本数量,样本多了,噪声比中就减少了
- 减少特征维数,高维空间密度小
- 加入正则化项,使得模型更加平滑
高偏差,低方差
- 寻找更好的特征,提升对数据的刻画能力
- 增加特征数量
- 重新选择更加复杂的模型
备注:通过好的模型验证方法,比如通过交叉验证法(可以解决了variance不同训练集学得的函数的差异,bias不同函数的平均值)的问题。
能更准确反映模型的误差,更精确的做误差分析
具体方法有:
- Holdout检验
- 交叉验证
- 自助法
评估指标数值多少合适?
我相信很多做机器学习算法模型的同学,都会疑惑我做好的模型,选择好了评估指标,最终得到的数值,我怎么去衡量这个数值对于模型性能来说是好是坏。
对于像均方误差、平均绝对误差、方均根差这样的评估指标是不能够告诉你,这个模型性能是否好坏的,它们的作用之一,是用来做比较的。也就是说,在优化模型或者更改一下模型参数后,用这些指标,对模型前后的指标数值进行对比。
在线性回归模型中起到决定性评估模型好坏的指标是R平方
具体可以参考这篇文章
决定系数R方是否越大越好?