《python数据分析与挖掘实战》(一)1-5章

1 数据挖掘基础

1. 从大量数据中挖掘出其对决策的潜在关系，并将这些关系运用于决策模型，提供预测性决策支持的方法、工具和过程，这就是数据挖掘。

2. 数据挖掘的基本任务：分类与预测、聚类分析、关联规则、时序模式、偏差检测、智能推荐等。

3. 数据挖掘建模过程

   1. 定义挖掘目标

   2. 数据取样

   3. 数据探索

      异常值分析、缺失值分析、相关分析、周期性分析等(详见第3章)

   4. 数据预处理

      数据筛选、数据变量转换、缺失值处理、坏数据处理、数据标准化、主成分分析、属性选择、数据归约等(详见第3章)

   5. 挖掘建模

   6. 模型评价

      1. 从所建立模型中找出一个最好的
      2. 根据业务对模型进行解释和应用(详见第5章)

2 Python数据分析简介

2.1 函数式编程

map()

a=[1,2,3]
b=[i+2 for i in a]
#利用map()改写
b=map(lambda x:x+2)
b=list(b)

列表解析的本质是for循环，map()效率更高

reduce()

s=1
for i in range(1,n+1):
    s=s*i
#利用reduce()改写
from functools import reduce
#算出n的阶乘
reduce(lambda x,y:x*y,range(1,n+1))

filter()

b=[i for i in range(10) if i>5 and i<8]
#利用filter()改写
b=filter(lambda x:x>5 and x<8,range(10))
b=list(b)

3 数据探索

3.1 数据质量分析

3.1.1 缺失值分析

处理方式：

​ 删除存在缺失值的记录、对可能值进行插补、不处理。详见4.1.1节

查看缺失值：

describe()中的count是非空数值，通过与len作差可以得到缺失值数量。

3.1.2 异常值分析

1. 简单统计量分析

2. 3σ原则

   ​ 数据服从正态分布、在3σ原则下，异常值被定义为一组测定值中与平均值偏差超过三倍标准差的值。

   ​ 在正态分布的假设下，距离平均值3σ之外的值出现的概率为P(|x-μ|>3σ)≤0.003，属于极小个别的小概率事件。

   ​ 如果数据不服从正态分布，也可以用远离平均值的多少倍标准差来描述。

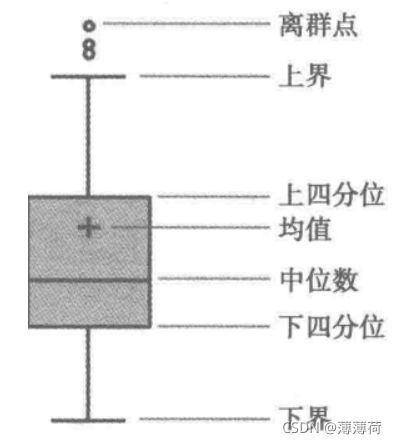
3. 箱形图分析

   ​ 异常值：小于$Q_L-1.5IQR$或大于$Q_U+1.5IQR$的值。

   $Q_L$：下四分位数，表示全部观察值中有四分之一的数据取值比它小。

   $Q_U$：上四分位数，表示全部观察值中有四分之一的数据取值比它大。

   $IQR$：四分位间距，是上四分位数和下四分位数之差。
   

餐饮数据异常值检测

import pandas as pd

catering_sale = './data/catering_sale.xls'  # 餐饮数据
data = pd.read_excel(catering_sale, index_col=u'日期')  # 读取数据，指定“日期”列为索引列

import matplotlib.pyplot as plt  # 导入图像库

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

plt.figure()  # 建立图像
p = data.boxplot(return_type='dict')  # 画箱线图，直接使用DataFrame的方法
x = p['fliers'][0].get_xdata()  # 'flies'即为异常值的标签
y = p['fliers'][0].get_ydata()
y.sort()  # 从小到大排序，该方法直接改变原对象

# 用annotate添加注释
# 其中有些相近的点，注解会出现重叠，难以看清，需要一些技巧来控制。
# 以下参数都是经过调试的，需要具体问题具体调试。
for i in range(len(x)):
    if i > 0:
        plt.annotate(y[i], xy=(x[i], y[i]), xytext=(x[i] + 0.05 - 0.8 / (y[i] - y[i - 1]), y[i]))
    else:
        plt.annotate(y[i], xy=(x[i], y[i]), xytext=(x[i] + 0.08, y[i]))

plt.show()  # 展示箱线图

结合实体业务，确定过滤规则为400以下5000以上为异常数据。

3.2 数据特征分析

3.2.1分布分析

​ 对于定量数据，欲了解其分布形式是对称还是非对称的，发现某些特大或特小的可疑值，可通过绘制频率分布表、频率分布直方图、茎叶图进行直观地分析。

​ 对于定性数据，可用饼图和条形图直观地显示分布情况。

1. 定量数据的分布分析

选择“组数”和“组宽”是做频率分析时最主要的问题，一般按以下步骤：

1. 求极差
2. 决定组距和组数
3. 决定分点
4. 列出频率分布表
5. 绘制频率分布直方图

要遵循以下原则：

1. 各组之间是相互排斥的。
2. 各组必须将所有的数据包含在内。
3. 各组的组宽最好相等
   

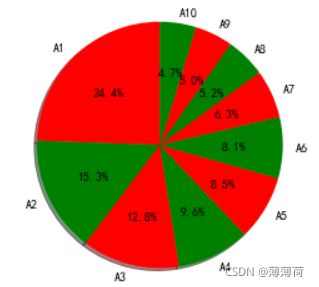
2. 定性数据的分布分析

import pandas as pd

dish_profit = './data/catering_dish_profit.xls' #餐饮菜品盈利数据
data = pd.read_excel(dish_profit, index_col = u'菜品名')
data = data[u'盈利'].copy()
data.sort_index(ascending = False)
sizes=[i/data.sum() for i in data]
colors=['red','green']
plt.pie(sizes,labels=data.index,colors=colors,autopct='%1.1f%%',shadow=True,startangle=90)
plt.axis('equal')

3.2.2 周期性的分析

用电量时序图

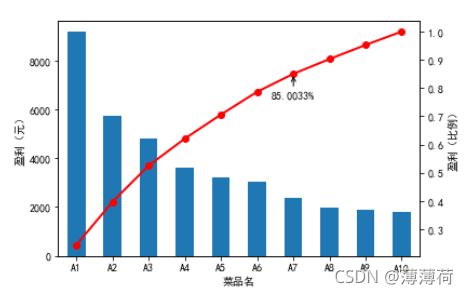
3.2.3 贡献度分析

又称帕累托分析，原理是帕累托法则，又称20/80定律。

plt.figure()
data.plot(kind='bar')
plt.ylabel(u'盈利（元）')
p = 1.0*data.cumsum()/data.sum()#计算占比
p.plot(color = 'r', secondary_y = True, style = '-o',linewidth = 2)
plt.annotate(format(p[6], '.4%'), xy = (6, p[6]), xytext=(6*0.9, p[6]*0.9), arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=0.02")) 
#添加注释，即85%处的标记。这里包括了指定箭头样式。
plt.ylabel(u'盈利（比例）')
plt.show()

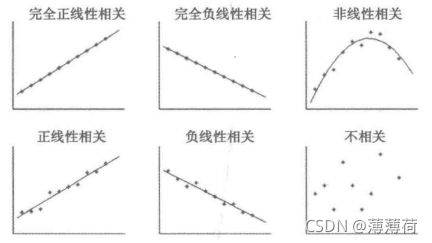
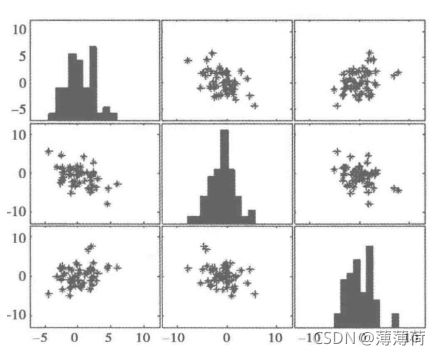
3.2.4 相关性分析

1. 绘制散点图

2. 绘制散点图矩阵
   

3. 计算相关系数

   1. Pearson相关系数

      1. 两个连续变量之间的关系
      2. 要求连续变量的取值服从正态分布

   2. Spearman秩相关系数

      1. 不服从正态分布的变量、分类或等级变量之间的关联性

   3. 判定系数

      1. 相关系数的平方，用来衡量回归方程对y的解释程度。

      2. $$判定系数取值范围：0\le r^2\le 1，越接近1相关性越强。$$

分析菜品销售量之间的相关性，得到不同菜品之间的关系。

菜品相关系数矩阵：

data.corr()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rwCR2avc-1630063913270)(C:\Users\86139\AppData\Roaming\Typora\typora-user-images\image-20210825152043826.png)]

• DF.coor()
  • 计算数据样本的Spearman(Pearson)相关数据矩阵。
  • method=""，支持pearson(默认)、kendall、spearman；
  • S1.coor(S2,method=“pearson”)

3.2 主要函数扩展

3.2.1统计作图函数

plot

功能：绘制线性二维图、折线图

使用格式：

• plt.plot(x,y,S)
  • S是字符串参量指定图形类型、样式、颜色，如：'b’为蓝色，‘+’为加号标记，‘o’为圆圈，‘–’为虚线，‘-’为实线。
• D.plt(kind=‘box’)
  • 默认以index为横坐标，每列数据为纵坐标，支持：line、bar、harh、hist、box、kde、area、pie等

pie

功能：绘制饼型图

使用格式：plt.pie(size)#size：各个扇形比例

labels='A','B','C','D'
sizes=[15,30,45,10]
colors=['yellow','gold','blue','green']
explode=(0,0.1,0,0)#突出显示，这里突出第二块
plt.pie(sizes,explode=explode,labels=labels,colors=colors,autopct='%1.1f%%',shadow=True,startangle=90)
plt.axis('equal')

tips：0-20等分成100份：x=np.linspace(0,20,100)

hist

功能：绘制二维条形直方图，可显示数据的分布情况

使用格式：plt.hist(x,y)

x是待绘制直方图的一维数组，y可以是整数，表示均分为y组，也可以是列表，列表各个数字为分组的边界点。

boxplot

功能：绘制样本数据的箱形图

使用格式：D.boxplot()/D.plot(kind=‘box’)

plot(logx=True)/plot(logy=True)

功能：绘制x或y轴的对数图形。

使用格式：D.plot(logx=True)

plot(yerr=error)

功能：绘制误差条形图

使用格式：D.plot(yerr=error)

如果设置参数xerr=error，则在x轴方向画出误差棒图。

4 数据预处理

4.1 数据清洗

​ 删除原始数据集中的无关数据、重复数据，平滑噪声数据，筛选掉与挖掘主题无关数据，处理缺失值、异常值等。

4.1.1 缺失值处理

插值法处理：拉格朗日插值法(Scipy支持)、牛顿插值法

# 自定义列向量插值函数
# s为列向量，n为被插值的位置，k为取前后的数据个数，默认为5
def ployinterp_column(s, n, k=5):
    y = s[list(range(n - k, n)) + list(range(n + 1, n + 1 + k))]  # 取数
    y = y[y.notnull()]  # 剔除空值
    return lagrange(y.index, list(y))(n)  # 插值并返回插值结果
# 逐个元素判断是否需要插值
for i in data.columns:
    for j in range(len(data)):
        if (data[i].isnull())[j]:  # 如果为空即插值。
            data.loc[[j], [i]] = ployinterp_column(data[i], j)

4.2 数据变换

4.2.1 规范化

不同评价指标往往具有不同量纲，不进行处理会影响数据分析结果。

• 最小-最大规范化

  • (data-data.min())/(data.max()-data.min())

• 零-均值规范化

  • (data-data.mean())/data.std()

• 小数定标规范化

  • data/10**np.ceil(np.log10(data.abs().max()))

4.2.2 连续属性离散化

有些数据挖掘算法，特别是某些分类算法(如ID3算法、Apripri算法等)，要求数据是分类属性形式，会用到将连续属性变换成分类属性的方法，即连续属性离散化。

1. 等宽法：将属性值域分成具有相同宽度的区间。
2. 等频法：将相同数量的记录放进每个区间。
3. 基于聚类分析的方法：
   1. 先将连续属性的值用聚类算法进行聚类。
   2. 再将聚类得到的簇合并到一个簇的连续属性值，并做同一标记。

# 等宽离散化，各个类比依次命名为0,1,2,3
d1 = pd.cut(data, k, labels=range(k))  

# 等频率离散化
w = [1.0 * i / k for i in range(k + 1)]
w = data.describe(percentiles=w)[4:4 + k + 1] 
w[0] = w[0] * (1 - 1e-10)
d2 = pd.cut(data, w, labels=range(k))

# KMeans
from sklearn.cluster import KMeans  
kmodel = KMeans(n_clusters=k, n_jobs=4)
kmodel.fit(data.values.reshape((len(data), 1))) 
c = pd.DataFrame(kmodel.cluster_centers_).sort_values(0)
w = c.rolling(2).mean().iloc[1:]
w = [0] + list(w[0]) + [data.max()]  # 把首末边界点加上
d3 = pd.cut(data, w, labels=range(k))

def cluster_plot(d, k):  # 自定义作图函数来显示聚类结果
    import matplotlib.pyplot as plt
    plt.figure(figsize=(8, 3))
    for j in range(0, k):
        plt.plot(data[d == j], [j for i in d[d == j]], 'o')
    plt.ylim(-0.5, k - 0.5)
    return plt

cluster_plot(d1, k).show()
cluster_plot(d2, k).show()
cluster_plot(d3, k).show()

4.3 数据规约

​ 数据规约产生更小但保持原数据完整性的新数据集。

4.3.1 属性规约

主成分分析

import pandas as pd

inputfile = './data/principal_component.xls'
data = pd.read_excel(inputfile, header=None)
from sklearn.decomposition import PCA
pca = PCA()
pca.fit(data)
pca.components_  # 返回模型的各个特征向量
pca.explained_variance_ratio_  # 返回各个成分各自的方差百分比

5 挖掘建模

5.1 常见的分类与预测算法

5.1.1 logistic回归

1. logistic回归属于概率型非线性回归。
2. 是可实现二分类或多分类的回归模型。

建模步骤：

1. 筛选数据、设置指标自变量和因变量、筛选特征。
2. 列出线性回归方程，估计出模型中的回归系数。
3. 模型检验：正确率、混淆矩阵、ROC曲线、KS值等。
4. 模型应用。

特征筛选：方法主要包含在Scikit_Learn的feature_selection库中

1. F检验(f_regression)：选择F值大或P值小的特征。
2. 递归特征消除
3. 稳定性选择

对银行降低贷款拖欠率的数据进行逻辑回归建模：

import pandas as pd
filename="./data/bankloan.xls"
data=pd.read_excel(filename)
x=data.iloc[:,:8]
y=data.iloc[:,8]

from sklearn.linear_model import LogisticRegression as LR
from sklearn.linear_model import RandomizedLogisticRegression as RLR
rlr=RLR()#随机逻辑回归模型，筛选变量
rlr.fit(x,y)
rlr.get_support()#获取特征筛选结果
#也可以通过.scores_方法获取各个特征的分数
rlr.scores_

print(u'有效特征为:%s' % ','.join(data.columns[rlr.get_support(indices=True)]))
#Indices是False，就返回一个类型是boolean的数组，如果indices是True,就返回一个整型数组
x=data.loc[:,data.columns[rlr.get_support(indices=True)]]

lr=LR()
lr.fit(x,y)
print("模型平均正确率：%s" % lr.score(x,y))

5.1.2 ID3算法

1. 基于信息熵来选择最佳测试属性，选最大信息增益值的属性作为测试属性。
2. 测试属性有多少不同取值就将样本集划分为多少子样本集。
3. 采用划分后样本集的不确定性作为划分好坏的标准，用信息增益度量不确定性。
4. 每个非叶节点选择信息增益最大的属性作为测试属性，得到最小的决策树。

import pandas as pd
filename='./data/sales_data.xls'
data=pd.read_excel(filename,index_col=u'序号')
#类别标签转换
data[data==u"好"]=1
data[data==u"是"]=1
data[data==u"高"]=1
data[data!=1]=-1
x=data.iloc[:,:3].astype(int)
y=data.iloc[:,3].astype(int)

from sklearn.tree import DecisionTreeClassifier as DTC
dtc=DTC(criterion='entropy')#基于信息熵
dtc.fit(x,y)

#导入相关函数，可视化决策树
# 导出的结果是dot文件，需安装Graphviz才能转换为pdf或png格式
from sklearn.tree import export_graphviz  # 导入可视化决策树
with open('tree.dot', 'w') as f:
    f = export_graphviz(dtc, feature_names=x.columns, out_file=f)

5.1.3 人工神经网络

import pandas as pd
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation  # 导入全连接层，激活层
from sklearn.metrics import confusion_matrix  # 导入混淆矩阵
import matplotlib.pyplot as plt
model=Sequential()
model.add(Dense(input_dim=3, units=10))
model.add(Activation('relu'))
model.add(Dense(input_dim=10, units=1))
model.add(Activation('sigmoid'))#0-1输出，用sigmoid做激活函数
model.compile(loss = 'binary_crossentropy', optimizer = 'adam')
#编译模型。二元分类，指定损失函数为binary_crossentropy，模式为binary
#另外常见的损失函数还有mean_squared_error、categorical_crossentropy等
#求解方法我们指定用adam，还有sgd、rmsprop等
model.fit(x, y, nb_epoch = 100, batch_size = 10) #训练模型，学习一千次
yp = model.predict_classes(x).reshape(len(y)) #分类预测

5.2 聚类分析

1. 聚类是在没有给定划分类别的情况下，根据数据相似度进行样本分组的方法。
2. 聚类模型可以建立在无类标记的数据上，是非监督学习。
3. 聚类划分原则：组内距离最小化，组间距离最大化。

5.2.1 K-Means

1. 对于连续属性，要先对各属性进行零-均值规范。
2. 使用误差平方和SSE作为度量聚类质量的目标函数。

# 使用K-Means算法聚类消费行为特征数据
import pandas as pd
inputfile = './data/consumption_data.xls'  # 销量及其他属性数据
# outputfile = './tmp/data_type.xls'  # 保存结果的文件名

k = 3  # 聚类的类别
iteration = 500  # 聚类最大循环次数
data = pd.read_excel(inputfile, index_col='Id')  # 读取数据
data_zs = 1.0 * (data - data.mean()) / data.std()  # 数据标准化

from sklearn.cluster import KMeans
model = KMeans(n_clusters=k, n_jobs=4, max_iter=iteration)  # 分为k类，并发数4
model.fit(data_zs)  # 开始聚类

# 简单打印结果
r1 = pd.Series(model.labels_).value_counts()  # 统计各个类别的数目
r2 = pd.DataFrame(model.cluster_centers_)  # 找出聚类中心
r = pd.concat([r2, r1], axis=1)  # 横向连接（0是纵向），得到聚类中心对应的类别下的数目
r.columns = list(data.columns) + [u'类别数目']  # 重命名表头
print(r)
# 详细输出原始数据及其类别
r = pd.concat([data, pd.Series(model.labels_, index=data.index)], axis=1)  # 详细输出每个样本对应的类别
r.columns = list(data.columns) + [u'聚类类别']  # 重命名表头
# r.to_excel(outputfile)  # 保存结果
r

TSNE提供有效数据降维方式，能在2维或3维空间中展示聚类结果。

from sklearn.manifold import TSNE

tsne = TSNE(random_state=0)
tsne.fit_transform(data_zs)  # 进行数据降维
tsne = pd.DataFrame(tsne.embedding_, index=data_zs.index)
plt.figure()

d = tsne[r[u'聚类类别'] == 0]
plt.plot(d[0], d[1], 'r.')

d = tsne[r[u'聚类类别'] == 1]
plt.plot(d[0], d[1], 'go')

d = tsne[r[u'聚类类别'] == 2]
plt.plot(d[0], d[1], 'b*')

# plt.show()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-v9C7ue8m-1630063913274)(C:\Users\86139\AppData\Roaming\Typora\typora-user-images\image-20210827111149254.png)]

5.3 关联规则

5.3.1 Apriori

from __future__ import print_function
import pandas as pd
# from apriori import *  # 导入自行编写的apriori函数

inputfile = r'.\data\menu_orders.xls'
outputfile = r'.\data\apriori_rules.xls'
data = pd.read_excel(inputfile, header=None)  # 读取数据
print(data)
print(u'\n转换原始数据至0-1矩阵...')
ct = lambda x: pd.Series(1, index=x[pd.notnull(x)])  # 转换0-1矩阵的过滤函数
b = list(map(ct, data.values))  # 用map方式执行
data = pd.DataFrame(b).fillna(0)  # 实现矩阵转换，空值用0填充
print(u'\n转换完毕.')
print(data)
print(data.sum(),len(data))
del b  # 删除中间变量b节省内存

support = 0.2 # 最小支持度
confidence = 0.5 # 最小执行度
ms = '---' # 连接符，默认’--‘ ，用来区分不同元素，如A--B.需要爆照原始表格中不含有该字符
find_rule(data,support,confidence,ms).to_excel(outputfile) # 保存结果

5.4 时序模式

5.4.1 预处理

1. 拿到一个观察值序列，首先进行纯随机性和平稳性检验，将序列分为不同类型后采用不同的分析方法：

   1. 白噪声序列：无分析价值。
   2. 平稳非白噪声序列：AR、MA、ARMA进行拟合。
   3. 非平稳序列：转变为平稳序列进行分析。若经差分运算后具有平稳性(差分平稳序列)，可使用ARIMA模 型。

   差分法：时间序列在t与t-1时刻的差值。

2. 平稳性检验：

   1. 时序图检验
   2. 自相关ACF图、偏自相关PACF图检验
   3. 单位根检验：选取标准为0.05,大于0.05则认为非平稳
   • 平稳性：
     • 要求经由样本时间序列所得到的拟合曲线在未来的一段时间内仍能顺着现有的形态“惯性”地延续下去。
     • 平稳性要求序列的均值和方差不发生明显变化。

• 模型
  • 自回归模型(AR)：
    • 描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测。
    • 限制：
      • 用自身数据来进行预测。
      • 必须满足平稳性的要求。
      • 必须具有相关性，如果相关系数小于0.5，则不宜采用。
      • 只适用于预测与自身前期相关的现象。
  • 移动平均模型(MA)：
    • 关注的是自回归模型中的误差项的累加，不考虑历史数据的影响。
    • 移动平均法能有效消除预测中的随机波动。
  • 自回归移动平均(ARMA)
  • 差分自回归移动平均模型(ARIMA):
    • AR是自回归，p为自回归项；MA为移动平均，q为移动平均项数，d为时间序列成为平稳时所做的差分次数。
    • 原理：将非平稳时间序列转化为平稳时间序列然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。
• 相关函数评估方法：
  • 自相关函数ACF：
    • 有序的随机变量序列与其自身相比较。
    • 自相关系数反映了同一序列在不同时序取值之间的相关性。
  • 偏自相关函数(PACF)：
    • ACF还包含了其他变量的影响，而偏自相关系数PACF是严格这两个变量之间的相关性。
• ARIMA(p，d，q)阶数确定：

模型	ACF	PACF
AR§	衰减趋于零(几何型或振荡型)	p阶后截尾
MA(q)	q阶后截尾	衰减趋于零(几何型或振荡型)
ARMA(p,q)	q阶后衰减趋于零(几何型或振荡型)	p阶衰减趋于零(几何型或振荡型)

截尾：落在置信区间内(95%的点都符合规则)

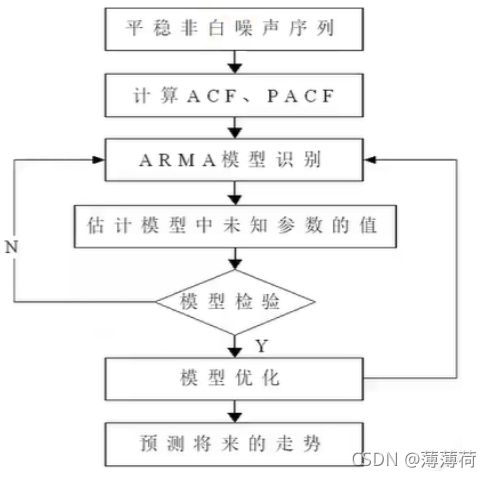
5.4.2 ARIMA

ARIMA建模流程：

1. 将序列平稳(差分法确定d)
2. 白噪声检验
3. 计算ACF、PACF
4. 模型识别
5. 参数估计
6. 模型检验
7. 模型优化
8. 模型预测
   

# arima时序模型
import pandas as pd
discfile = './data/arima_data.xls'
forecastnum = 5
data = pd.read_excel(discfile, index_col=u'日期')
data.head(3)
# 时序图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
data.plot()
plt.show()
# 差分后的结果
D_data = data.diff().dropna()#diff默认值是1，默认一阶差分
D_data.columns = [u'销量差分']
D_data.plot()  # 时序图
plot_acf(D_data)  # 自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data,lags=12)  # 偏自相关图，显示前20个
plot_pacf(D_data)  # 偏自相关图，显示所有元素
print(u'差分序列的ADF检验结果为：',ADF(D_data[u'销量差分']))  # 平稳性检测
#pvalue单位根选取标准为0.05,小于0.05则认为平稳
#只用了一阶差分，所以d=1
# 白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1))  # 返回统计量和p值
#p值小于0.05，认为不是白噪声序列
from statsmodels.tsa.arima_model import ARIMA

#定阶
pmax = int(len(data)/10) #一般阶数不超过length/10
qmax = int(len(data)/10) #一般阶数不超过length/10
bic_matrix = [] #bic矩阵
for p in range(pmax+1):
    tmp = []
    for q in range(qmax+1):
        try: #存在部分报错，所以用try来跳过报错。
            tmp.append(ARIMA(data, (p,1,q)).fit().bic)
        except:
            tmp.append(None)
    bic_matrix.append(tmp)
print(bic_matrix)
from statsmodels.tsa.arima_model import ARIMA
# 定阶，自相关系数和偏自相关系数究竟是截尾还是拖尾
data['销量'] = data['销量'].astype(float)
pmax = int(len(D_data) / 10)  # 一般阶数不超过length/10
qmax = int(len(D_data) / 10)  # 一般阶数不超过length/10
bic_matrix = []  # bic矩阵
for p in range(pmax + 1):
    tmp = []
    for q in range(qmax + 1):
        try:  # 存在部分报错，所以用try来跳过报错。
            tmp.append(ARIMA(data, (p, 1, q)).fit().bic)
        except:
            tmp.append(None)
    bic_matrix.append(tmp)
bic_matrix = pd.DataFrame(bic_matrix)  # 从中可以找出最小值
p, q = bic_matrix.stack().idxmin()  # 先用stack展平，然后用idxmin找出最小值位置。
print(u'BIC最小的p值和q值为：%s、%s' % (p, q))#得到p、q；p自相关系数，q偏自相关系数
model = ARIMA(data, (p, 1, q)).fit()  # 建立ARIMA(0, 1, 1)模型
model.summary2()  # 给出一份模型报告
model.forecast(5)  # 作为期5天的预测，返回预测结果、标准误差、置信区间。

预测结果4873.9665477在置信区间[4730.72112437, 5017.21197102]内，预测结果是较为准确的。

5.5 离群点检测

• 发现与大部分其他对象显著不同的对象。
• 也称为偏差检测，广泛应用于电信和信用卡的诈骗检测、贷款审批、电子商务、网络入侵和天气预报等领域。

5.5.1 基于聚类的离群点检测

1. 丢弃远离其他簇的小簇：
   1. 丢弃小于某个阈值的所有簇，对聚类簇数k的选择高度敏感。
2. 基于原型的聚类：
   1. 首先聚类所有对象，然后评估对象属于簇的程度(离群点得分)。离群点得分主要有两种：
      1. 度量对象到簇原型的距离。
      2. 度量簇到原型的相对距离：点到质心的距离与簇中所有点到质心的距离的中位数之比。
   2. 如果删除一个对象导致该目标显著改进，则将该对象视为离群点。
      1. 如，在k均值算法中，删除远离其相关簇中心的对象能够显著地改进该簇的误差平方和SSE。
   3. 诊断步骤：
      1. 进行聚类。选择聚类算法，将样本聚为K簇，找到各簇的质心。
      2. 计算各对象到它的最近的质心距离。
      3. 计算各对象到它的最近质心的相对距离。
      4. 与给定阈值作比较。

import numpy as np
import pandas as pd
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt  # 带入图像库
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文指标
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号

inputfile = r'.\data\consumption_data.xls'
k = 3 #聚类的类别
threshold = 2 # 离群点阈值
iteration = 500 # 聚类最大循环次数
readExcel = pd.ExcelFile(inputfile)
data = pd.read_excel(readExcel,index_col='Id')#读取数据
data_zs = 1.0*(data-data.mean(axis=0))/data.std(axis=0) # 标准差标准化

model = KMeans(n_clusters=k,n_jobs=4,max_iter=iteration)
model.fit(data_zs)

r = pd.concat([data_zs,pd.Series(model.labels_,index=data.index)],axis = 1)
r.columns = list(data.columns) + [u'聚类类别']

norm =[]
for i in range(k):
    norm_tmp = r[['R','F','M']][r[u'聚类类别'] == i]-model.cluster_centers_[i]
    norm_tmp = norm_tmp.apply(np.linalg.norm,axis=1)
    norm.append(norm_tmp/norm_tmp.median())#求相对距离并添加

norm = pd.concat(norm) # 合并
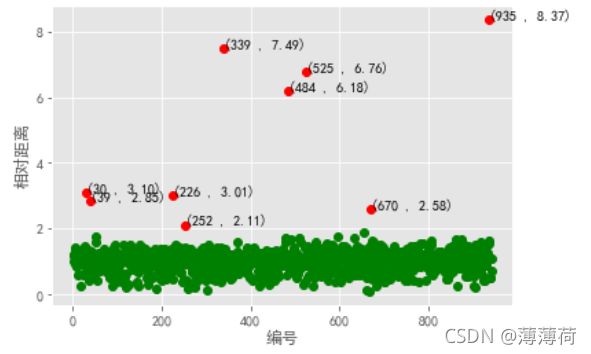
norm[norm <= threshold].plot(style = 'go' ) #正常点

discrete_points = norm[norm>threshold]
discrete_points.plot(style='ro')#离群点

for i in range(len(discrete_points)):
    id = discrete_points.index[i]
    n = discrete_points.iloc[i]
    plt.annotate('(%s , %0.2f)'%(id,n),xy = (id,n),xytext = (id,n))
plt.xlabel(u'编号')
plt.ylabel(u'相对距离')
plt.show()