Tensorflow学习笔记(二):神经网络优化
文章目录
- 一、预备知识
-
- 1. 条件判断和选择(where)
- 2. [0, 1)随机数(random.RandomState.rand)
- 3. 数组垂直叠加(vstack)
- 4. 网格生成(mgrid,ravel,c_)
- 二、神经网络复杂度、学习率选取
-
- 1. 复杂度
- 2. 学习率更新
-
- (1)影响
- (2)更新策略
- 三、激活函数、损失函数
-
- 1. 几种激活函数介绍
-
- (1) Sigmoid函数
- (2) tanh函数
- (3) ReLu函数
- (4) Leaky-ReLu
- (5) 激活函数选择建议
- 2. 几类损失函数
-
- (1)均方误差MSE
- (2)交叉熵CE
- 四、缓解过拟合:正则化
-
- 1. 欠拟合、过拟合
- 2. 正则化
-
- (1)原理
- (2)代码实现
- (3)结果比较
- 五、神经网络参数优化器
-
- 1. 参数更新过程
- 2. 常用优化器
-
- (1)SGD
- (2)SGDM
- (3)Adagrad
- (4)RMSProp
- (5)Adam
- 3. 常用优化器比较
本文是个人的学习笔记,是跟随北大曹健老师的视频课学习的
链接: 人工智能实践:Tensorflow笔记(北京大学 软件与微电子学院 曹健老师)
一、预备知识
1. 条件判断和选择(where)
a = tf.constant([1, 2, 3, 1, 1])
b = tf.constant([0, 1, 3, 4, 5])
c = tf.where(tf.greater(a, b), a, b) # 条件?T/N
print('c:{}'.format(c))
结果
c:[1 2 3 4 5]
2. [0, 1)随机数(random.RandomState.rand)
rdm = np.random.RandomState()
a = rdm.rand() # scalar
b = rdm.rand(2, 3)
print('a={},\n b={}'.format(a, b))
结果
a=0.7902641789078835,
b=[[0.25573684 0.43114347 0.05323669]
[0.93982238 0.01915588 0.99566242]]
3. 数组垂直叠加(vstack)
rdm = np.random.RandomState()
a = rdm.rand(3)
b = rdm.rand(3)
c = np.vstack((a, b))
print('a={}, b={}, \nc={}'.format(a, b, c))
结果
a=[0.61471964 0.41927043 0.76723631], b=[0.44699221 0.00728193 0.60133098],
c=[[0.61471964 0.41927043 0.76723631]
[0.44699221 0.00728193 0.60133098]]
4. 网格生成(mgrid,ravel,c_)
x, y = np.mgrid[1:3, 2:4:0.5]
grid = np.c_[x.ravel(), y.ravel()]
print('x={},\ny={},\ngrid={}'.format(x, y, grid))
结果
x=[[1. 1. 1. 1.]
[2. 2. 2. 2.]],
y=[[2. 2.5 3. 3.5]
[2. 2.5 3. 3.5]],
grid=[[1. 2. ]
[1. 2.5]
[1. 3. ]
[1. 3.5]
[2. 2. ]
[2. 2.5]
[2. 3. ]
[2. 3.5]]
二、神经网络复杂度、学习率选取
1. 复杂度
空间:层数;时间:乘加运算次数。
2. 学习率更新
(1)影响
学习率过小 → \rightarrow →更新过慢;学习率过大 → \rightarrow →不收敛
(2)更新策略
这里老师推荐了指数衰减学习率
l r = l r 0 a , a = e p o c h / u p d a t e s t e p lr=lr_0^a, ~~~~~a={epoch}/{update~step} lr=lr0a, a=epoch/update step
代码实现
for epoch in range(epoches): # 每一次epoch遍历一次数据集
Loss = 0
lr = lr_base * lr_decay ** (epoch / lr_step)
for step, (x_train, y_train) in enumerate(data_train): # 每一个step遍历一个batch
...
print('After {} epoch, lr={}'.format(epoch, w1, lr))
结果
After 0 epoch, lr=0.2
After 1 epoch, lr=0.198
After 2 epoch, lr=0.19602
After 3 epoch, lr=0.1940598
After 4 epoch, lr=0.192119202
After 5 epoch, lr=0.19019800998
After 6 epoch, lr=0.1882960298802
After 7 epoch, lr=0.186413069581398
After 8 epoch, lr=0.18454893888558402
After 9 epoch, lr=0.18270344949672818
...
After 90 epoch, lr=0.08094639453566477
After 91 epoch, lr=0.08013693059030812
After 92 epoch, lr=0.07933556128440503
After 93 epoch, lr=0.07854220567156098
After 94 epoch, lr=0.07775678361484537
After 95 epoch, lr=0.07697921577869692
After 96 epoch, lr=0.07620942362090993
After 97 epoch, lr=0.07544732938470083
After 98 epoch, lr=0.07469285609085384
After 99 epoch, lr=0.07394592752994529
三、激活函数、损失函数
1. 几种激活函数介绍
(1) Sigmoid函数
y = σ ( x ) = 1 1 + e − x , d y d x = σ ′ ( x ) = y ( 1 − y ) y=\sigma(x)=\frac{1}{1+e^{-x}},~~~~\frac{dy}{dx}=\sigma'(x)=y(1-y) y=σ(x)=1+e−x1, dxdy=σ′(x)=y(1−y)
简证
σ ′ ( x ) = d d x ( 1 + e − x ) − 1 = − ( 1 + e − x ) − 2 ⋅ e − x ⋅ ( − 1 ) = e − x ( 1 + e − x ) 2 = 1 1 + e − x e − x 1 + e − x = 1 1 + e − x ( 1 − 1 1 + e − x ) = y ( 1 − y ) \sigma'(x)=\frac{d}{dx}(1+e^{-x})^{-1}=-(1+e^{-x})^{-2}\cdot e^{-x}\cdot (-1)=\frac{e^{-x}}{(1+e^{-x})^2}=\frac{1}{1+e^{-x}}\frac{e^{-x}}{1+e^{-x}}=\frac{1}{1+e^{-x}}(1-\frac{1}{1+e^{-x}})=y(1-y) σ′(x)=dxd(1+e−x)−1=−(1+e−x)−2⋅e−x⋅(−1)=(1+e−x)2e−x=1+e−x11+e−xe−x=1+e−x1(1−1+e−x1)=y(1−y)

特点:易造成梯度消失(导数值小于1,多层相乘之后趋于0);输出非0均值,收敛慢(一般数据都是服从标准正态分布的);幂运算复杂,训练时间长
(2) tanh函数
y = t a n h ( x ) = e x − e − x e x − e − x = 1 − e − 2 x 1 + e − 2 x , d y d x = t a n h ′ ( x ) = 1 − y 2 y=tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}-e^{-x}}=\frac{1-e^{-2x}}{1+e^{-2x}},~~~~\frac{dy}{dx}=tanh'(x)=1-y^2 y=tanh(x)=ex−e−xex−e−x=1+e−2x1−e−2x, dxdy=tanh′(x)=1−y2
简证:注意到 σ ( x ) + σ ( − x ) = 1 \sigma(x)+\sigma(-x)=1 σ(x)+σ(−x)=1
t a n h ( x ) = 1 1 + e − 2 x − e − 2 x 1 + e − 2 x = 1 1 + e − 2 x − 1 1 + e 2 x = σ ( 2 x ) − σ ( − 2 x ) = 2 ⋅ σ ( 2 x ) − 1 tanh(x)=\frac{1}{1+e^{-2x}}-\frac{e^{-2x}}{1+e^{-2x}}=\frac{1}{1+e^{-2x}}-\frac{1}{1+e^{2x}}=\sigma(2x)-\sigma(-2x)=2\cdot\sigma(2x)-1 tanh(x)=1+e−2x1−1+e−2xe−2x=1+e−2x1−1+e2x1=σ(2x)−σ(−2x)=2⋅σ(2x)−1
由(1)中结论: σ ′ ( x ) = σ ( x ) ( 1 − σ ( x ) ) = σ ( x ) σ ( − x ) \sigma'(x)=\sigma(x)(1-\sigma(x))=\sigma(x)\sigma(-x) σ′(x)=σ(x)(1−σ(x))=σ(x)σ(−x),因此有
d d x σ ( 2 x ) = 2 ⋅ σ ( 2 x ) σ ( − 2 x ) , d d x σ ( − 2 x ) = − 2 ⋅ σ ( − 2 x ) σ ( 2 x ) \frac{d}{dx}\sigma(2x)=2\cdot\sigma(2x)\sigma(-2x),~~~~\frac{d}{dx}\sigma(-2x)=-2\cdot\sigma(-2x)\sigma(2x) dxdσ(2x)=2⋅σ(2x)σ(−2x), dxdσ(−2x)=−2⋅σ(−2x)σ(2x)
由此得到
t a n h ′ ( x ) = 4 ⋅ σ ( 2 x ) σ ( − 2 x ) = 4 ⋅ σ ( 2 x ) ( 1 − σ ( 2 x ) ) = 1 − [ 1 − 2 ⋅ 2 ⋅ σ ( 2 x ) + ( 2 ⋅ σ ( 2 x ) ) 2 ] = 1 − ( 2 ⋅ σ ( 2 x ) − 1 ) 2 = 1 − t a n h 2 ( x ) tanh'(x)=4\cdot\sigma(2x)\sigma(-2x)=4\cdot\sigma(2x)(1-\sigma(2x))=1-[1-2\cdot2\cdot\sigma(2x)+(2\cdot\sigma(2x))^2]=1-(2\cdot\sigma(2x)-1)^2=1-tanh^2(x) tanh′(x)=4⋅σ(2x)σ(−2x)=4⋅σ(2x)(1−σ(2x))=1−[1−2⋅2⋅σ(2x)+(2⋅σ(2x))2]=1−(2⋅σ(2x)−1)2=1−tanh2(x)
相对于直接求导来说这个过程有些复杂,但应用了Sigmoid函数的一些性质,以及两个函数的一些关系。

特点:输出是0均值;易造成梯度消失;幂运算复杂,训练时间长
(3) ReLu函数
y = = m a x ( 0 , x ) , d y d x = 1 ( i f x ≥ 0 ) o r 0 ( e l s e ) = 1 2 ( s i g n ( x ) + 1 ) y==max(0, x),~~~~\frac{dy}{dx}=1(if ~x≥0) ~or~0(else)=\frac{1}{2}(sign(x)+1) y==max(0,x), dxdy=1(if x≥0) or 0(else)=21(sign(x)+1)
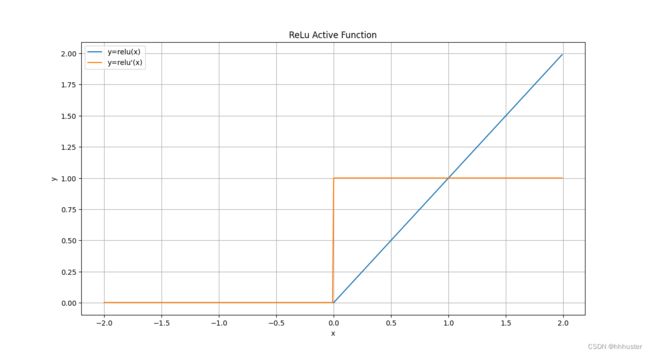
优点:解决了梯度消失(正区间);只需判断输入是否大于0,计算速度快;收敛速度远快于sigmoid&tanh
缺点:输出非0均值,收敛慢;Dead ReLu:某些神经元可能永远不激活,对应参数永远不更新(可以通过改进初始化、改变学习率等方式减少负数特征缓解)
(4) Leaky-ReLu
y = m a x ( α x , x ) , d y d x = 1 ( i f x ≥ 0 ) o r α ( e l s e ) ( α > 0 ) y=max(\alpha x, x),~~~~\frac{dy}{dx}=1(if ~x≥0) ~or~\alpha(else)~~~(\alpha>0) y=max(αx,x), dxdy=1(if x≥0) or α(else) (α>0)

实践中证明未必一定好于ReLu函数
(5) 激活函数选择建议
- 首选ReLu
- learning rate设置较小值
- 输入特征标准化, x ∼ N ( 0 , 1 ) x ∼ N(0,1) x∼N(0,1)
- 初始参数中心化, x ∼ N ( 0 , 2 / d ) , d x ∼ N(0,\sqrt{2/d}), d x∼N(0,2/d),d为当前层输入特征个数
2. 几类损失函数
损失函数(Loss):预测 y ^ \hat y y^和实际 y y y的差距,神经网络优化目标为Loss最小。
(1)均方误差MSE
函数具体形式为 L M S E ( y , y ^ ) = 1 N ∑ N ( y − y ^ ) 2 , ∇ L y ^ = 2 N ∑ N ( y ^ − y ) L_{MSE}(y, \hat y)=\frac{1}{N}\sum^N(y-\hat y)^2,~~~~\nabla L_{\hat y}=\frac{2}{N}\sum^N(\hat y-y) LMSE(y,y^)=N1∑N(y−y^)2, ∇Ly^=N2∑N(y^−y)
代码实现
with tf.GradientTape() as tape:
...
loss = tf.reduce_mean(tf.square(y - y0)) # 计算loss
grads = tape.gradient(loss, para) # 计算梯度
(2)交叉熵CE
函数具体形式为 L C E ( y , y ^ ) = − ∑ d y ⋅ l n y ^ , ∇ L y ^ = − ∑ d y y ^ L_{CE}(y, \hat y)=-\sum^d y\cdot ln\hat y,~~~~\nabla L_{\hat y}=-\sum^d \frac{y}{\hat y} LCE(y,y^)=−∑dy⋅lny^, ∇Ly^=−∑dy^y
代码实现
with tf.GradientTape() as tape:
...
loss = tf.reduce_mean(tf.square(y - y0)) # 计算loss
grads = tape.gradient(loss, para) # 计算梯度
常常与Softmax结合,如
y0 = np.array([[1, 0, 0], [0, 1, 0], [0, 0, 1], [1, 0, 0], [0, 1, 0]])
y_train = np.array([[12, 3, 2], [3, 10, 1], [1, 2, 5], [4, 6.5, 1.2], [3, 6, 1]])
y = tf.nn.softmax(y_train)
loss1 = tf.losses.categorical_crossentropy(y0, y)
loss2 = tf.nn.softmax_cross_entropy_with_logits(y0, y_train)
结果
loss1=[1.68795487e-04 1.03475622e-03 6.58839038e-02 2.58349207e+00 5.49852354e-02]
loss2=[1.68795487e-04 1.03475622e-03 6.58839038e-02 2.58349207e+00 5.49852354e-02]
四、缓解过拟合:正则化
1. 欠拟合、过拟合
-
欠拟合:拟合不好,学习不够
解决:增加输入特征、网络参数,减少正则化参数 -
过拟合:泛化能力差
解决:数据清洗(去噪),增大训练集,采用正则化、增大正则化参数
2. 正则化
在损失函数中引入模型复杂度指标(给w加权值不给b加,抑制噪声)
(1)原理
L o s s = L ( y , y ^ ) + R e g u l a r i z e r × l o s s ( w ) Loss=L(y, \hat y)+Regularizer×loss(w) Loss=L(y,y^)+Regularizer×loss(w)
其中, L ( ⋅ ) L(\cdot) L(⋅)为上述介绍的几种损失函数, R e g u l a r i z e r Regularizer Regularizer为超参数, l o s s l k ( w ) = ∑ ∣ w i k ∣ loss_{l_k}(w)=\sum|w_i^k| losslk(w)=∑∣wik∣
L 1 L_1 L1正则化大概率把很多参数清零:减少参数数量,降低复杂度
L 2 L_2 L2正则化使很多参数接近零:减少参数大小,降低复杂度
(2)代码实现
对 M S E MSE MSE损失函数,叠加 L 2 L_2 L2正则化
loss_mse = tf.reduce_mean(tf.square(y - label_train))
loss_regularization = []
# tf.nn.l2_loss(w)=sum(w ** 2) / 2
loss_regularization.append(tf.nn.l2_loss(w1))
loss_regularization.append(tf.nn.l2_loss(w2))
# 求和
loss_regularization = tf.reduce_sum(loss_regularization)
loss = loss_mse + regularizer * loss_regularization # REGULARIZER = 0.03
(3)结果比较
分别不使用正则化和使用正则化,生成可视化结果,可以看出,引入正则化后,过拟合现象明显缓解,分类面明显更加光滑
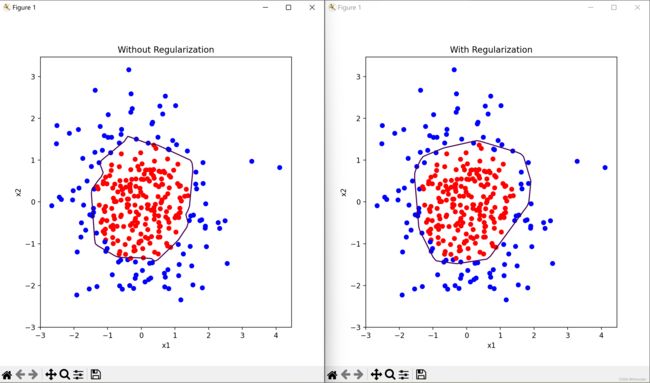
附代码:正则化处理之前
import tensorflow as tf
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
# 读入数据集
database = pd.read_csv('dot.csv')
data = np.array(database[['x1', 'x2']])
label = np.array(database['y_c'])
# reshape参数中-1表示根据另一个参数确定形状
data_train = np.vstack(data).reshape(-1, 2)
label_train = np.vstack(label).reshape(-1, 1)
label_color = [['red' if y else 'blue'] for y in label_train]
# 转换数据类型,生成规范数据集
data_train = tf.cast(data_train, tf.float32)
label_train = tf.cast(label_train, tf.float32)
dataset_train = tf.data.Dataset.from_tensor_slices((data_train, label_train)).batch(32)
# 建立神经网络,2-11-1
# 参数初始化
w1 = tf.Variable(tf.random.normal([2, 11]), dtype=tf.float32)
b1 = tf.Variable(tf.constant(0.01, shape=[11]))
w2 = tf.Variable(tf.random.normal([11, 1]), dtype=tf.float32)
b2 = tf.Variable(tf.constant(0.01, shape=[1]))
# 超参数
lr = 0.005
epoches = 800
regularizer = 0.03
# 训练
for epoch in range(epoches):
for step, (data_train, label_train) in enumerate(dataset_train):
with tf.GradientTape() as tape:
# 前向
s1 = tf.matmul(data_train, w1) + b1
s1 = tf.nn.relu(s1)
y = tf.matmul(s1, w2) + b2
# 采用均方误差损失函数mse
loss = tf.reduce_mean(tf.square(label_train - y))
# 计算loss对各个参数的梯度
variables = [w1, b1, w2, b2]
grads = tape.gradient(loss, variables)
# 反向梯度更新
w1.assign_sub(lr * grads[0])
b1.assign_sub(lr * grads[1])
w2.assign_sub(lr * grads[2])
b2.assign_sub(lr * grads[3])
if epoch % 20 == 0:
print('epoch:', epoch, 'loss:', float(loss))
# 测试
print("*******predict*******")
# 创建网格数据
xx, yy = np.mgrid[-3:3:.1, -3:3:.1]
grid = np.c_[xx.ravel(), yy.ravel()]
grid = tf.cast(grid, tf.float32)
label_test = []
for data_test in grid:
h1 = tf.matmul([data_test], w1) + b1
h1 = tf.nn.relu(h1)
y = tf.matmul(h1, w2) + b2
label_test.append(y)
x1 = data[:, 0]
x2 = data[:, 1]
plt.scatter(x1, x2, color=np.squeeze(label_color))
label_test = np.array(label_test).reshape(xx.shape)
plt.contour(xx, yy, label_test, levels=[.5])
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('Without Regularization')
plt.show()
正则化处理之后
import tensorflow as tf
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
# 读入数据集
database = pd.read_csv('dot.csv')
data = np.array(database[['x1', 'x2']])
label = np.array(database['y_c'])
# reshape参数中-1表示根据另一个参数确定形状
data_train = np.vstack(data).reshape(-1, 2)
label_train = np.vstack(label).reshape(-1, 1)
label_color = [['red' if y else 'blue'] for y in label_train]
# 转换数据类型,生成规范数据集
data_train = tf.cast(data_train, tf.float32)
label_train = tf.cast(label_train, tf.float32)
dataset_train = tf.data.Dataset.from_tensor_slices((data_train, label_train)).batch(32)
# 建立神经网络,2-11-1
# 参数初始化
w1 = tf.Variable(tf.random.normal([2, 11]), dtype=tf.float32)
b1 = tf.Variable(tf.constant(0.01, shape=[11]))
w2 = tf.Variable(tf.random.normal([11, 1]), dtype=tf.float32)
b2 = tf.Variable(tf.constant(0.01, shape=[1]))
# 超参数
lr = 0.005
epoches = 800
regularizer = 0.03
# 训练
for epoch in range(epoches):
for step, (data_train, label_train) in enumerate(dataset_train):
with tf.GradientTape() as tape:
# 前向
s1 = tf.matmul(data_train, w1) + b1
s1 = tf.nn.relu(s1)
y = tf.matmul(s1, w2) + b2
# 采用均方误差损失函数mse
loss_mse = tf.reduce_mean(tf.square(label_train - y))
loss_regularization = []
# tf.nn.l2_loss(w)=sum(w ** 2) / 2
loss_regularization.append(tf.nn.l2_loss(w1))
loss_regularization.append(tf.nn.l2_loss(w2))
# 求和
loss_regularization = tf.reduce_sum(loss_regularization)
loss = loss_mse + regularizer * loss_regularization # REGULARIZER = 0.03
# 计算loss对各个参数的梯度
variables = [w1, b1, w2, b2]
grads = tape.gradient(loss, variables)
# 反向梯度更新
w1.assign_sub(lr * grads[0])
b1.assign_sub(lr * grads[1])
w2.assign_sub(lr * grads[2])
b2.assign_sub(lr * grads[3])
if epoch % 20 == 0:
print('epoch:', epoch, 'loss:', float(loss))
# 测试
print("*******predict*******")
# 创建网格数据
xx, yy = np.mgrid[-3:3:.1, -3:3:.1]
grid = np.c_[xx.ravel(), yy.ravel()]
grid = tf.cast(grid, tf.float32)
label_test = []
for data_test in grid:
h1 = tf.matmul([data_test], w1) + b1
h1 = tf.nn.relu(h1)
y = tf.matmul(h1, w2) + b2
label_test.append(y)
x1 = data[:, 0]
x2 = data[:, 1]
plt.scatter(x1, x2, color=np.squeeze(label_color))
label_test = np.array(label_test).reshape(xx.shape)
plt.contour(xx, yy, label_test, levels=[.5])
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('With Regularization')
plt.show()
五、神经网络参数优化器
本届使用的源码与学习笔记(一)中【五、神经网络搭建与训练(一层)——1. 源码】相同,这里仅仅对优化器进行更改
1. 参数更新过程
对于待优化参数 w w w,损失函数 L L L,学习率 l r lr lr,每次迭代一个 b a t c h batch batch, t t t表示当前 b a t c h batch batch迭代总次数
- 计算 t t t时刻损失函数关于当前参数的梯度: g t = ∇ L w g_t=\nabla L_w gt=∇Lw
- 计算 t t t时刻一阶动量 m t m_t mt(和 g t g_t gt相关)和二阶动量 V t V_t Vt(和 g t 2 g_t^2 gt2相关)【对应不同种优化器】
- 计算 t t t时刻下降梯度: η t = l r ⋅ m t / V t \eta_t=lr\cdot m_t/ \sqrt{V_t} ηt=lr⋅mt/Vt
- 计算 t + 1 t+1 t+1时刻参数: w t + 1 = w t − η t w_{t+1}=w_t-\eta_t wt+1=wt−ηt
下面列举一些常见的优化器的动量表达形式,并用python实现
2. 常用优化器
(1)SGD
动量表达形式: m t = g t , V t = 1 ⇒ w t + 1 = w t − l r ⋅ g t m_t=g_t,~~V_t=1\Rightarrow w_{t+1}=w_t-lr\cdot g_t mt=gt, Vt=1⇒wt+1=wt−lr⋅gt
代码实现:
w1.assign_sub(lr * grads[0]) # 参数空间更新
b1.assign_sub(lr * grads[1])
训练结果为:训练时间 t S G D = 8.394366025924683 s t_{SGD}=8.394366025924683s tSGD=8.394366025924683s,两条曲线如图所示

(2)SGDM
动量表达形式: m t = β m t − 1 + ( 1 − β ) g t , V t = 1 ⇒ w t + 1 = w t − l r ⋅ m t m_t=\beta m_{t-1}+(1-\beta)g_t,~~V_t=1\Rightarrow w_{t+1}=w_t-lr\cdot m_t mt=βmt−1+(1−β)gt, Vt=1⇒wt+1=wt−lr⋅mt
代码实现:
# 初始化
mw, mb = 0, 0
beta = 0.9
...
mw = beta * mw + (1 - beta) * grads[0]
mb = beta * mb + (1 - beta) * grads[1] # 计算动量
w1.assign_sub(lr * mw) # 参数空间更新
b1.assign_sub(lr * mb)
训练结果为:训练时间 t S G D M = 9.672947883605957 s t_{SGDM}=9.672947883605957s tSGDM=9.672947883605957s,两条曲线如图所示
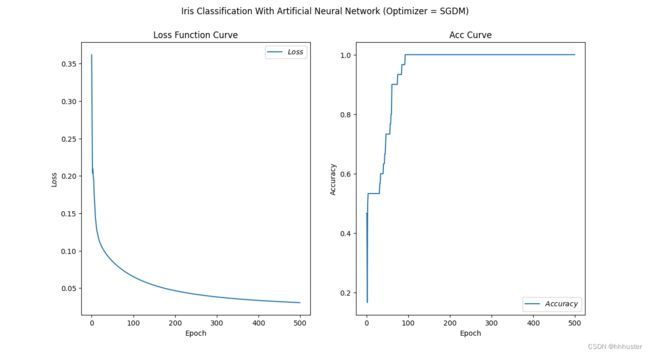
(3)Adagrad
动量表达形式: m t = g t , V t = ∑ τ = 1 t g τ 2 m_t=g_t,~~V_t=\sum_{\tau=1}^{t} g_\tau^2 mt=gt, Vt=∑τ=1tgτ2
代码实现:
# 初始化
vw, vb = 0, 0
...
vw += tf.square(grads[0])
vb += tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(vw)) # 参数空间更新
b1.assign_sub(lr * grads[1] / tf.sqrt(vb))
训练结果为:训练时间 t A d a g r a d = 9.278505802154541 s t_{Adagrad}=9.278505802154541s tAdagrad=9.278505802154541s,两条曲线如图所示

(4)RMSProp
动量表达形式: m t = g t , V t = β V t − 1 + ( 1 − β ) g t 2 m_t=g_t,~~ V_t=\beta V_{t-1}+(1-\beta)g_t^2 mt=gt, Vt=βVt−1+(1−β)gt2
代码实现:
# 初始化
vw, vb = 0, 0
beta = 0.9
...
vw = beta*vw + (1-beta) * tf.square(grads[0])
vb = beta*vb + (1-beta) * tf.square(grads[1])
w1.assign_sub(lr * grads[0] / tf.sqrt(vw)) # 参数空间更新
b1.assign_sub(lr * grads[1] / tf.sqrt(vb))
训练结果为:训练时间 t R M S P r o p = 9.854762315750122 s t_{RMSProp}=9.854762315750122s tRMSProp=9.854762315750122s,两条曲线如图所示
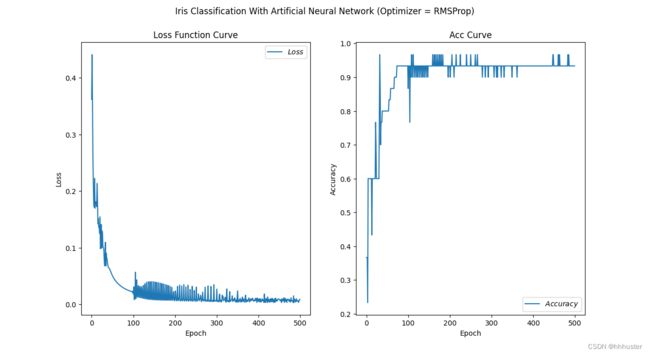
曲线振荡明显,因此调小学习率至 l r = 0.01 lr=0.01 lr=0.01,得到训练时间 t R M S P r o p ′ = 9.869148254394531 s t'_{RMSProp}=9.869148254394531s tRMSProp′=9.869148254394531s

(5)Adam
动量表达形式: m t = β 1 m t − 1 + ( 1 − β 1 ) g t , V t = β 2 V t − 1 + ( 1 − β 2 ) g t 2 m_t=\beta_1 m_{t-1}+(1-\beta_1)g_t,~~V_t=\beta_2 V_{t-1}+(1-\beta_2)g_t^2 mt=β1mt−1+(1−β1)gt, Vt=β2Vt−1+(1−β2)gt2
然后需要对动量进行修正: m ^ t = m t / ( 1 − β 1 t ) , V ^ t = V t / ( 1 − β 2 t ) \hat m_t=m_t/(1-\beta_1^t),~~\hat V_t=V_t/(1-\beta_2^t) m^t=mt/(1−β1t), V^t=Vt/(1−β2t)
注意这里的 m ^ t , V ^ t \hat m_t,~~\hat V_t m^t, V^t仅仅在更新权重时使用,而动量更新则用修正前的,在编写程序时要注意
更新时: w t + 1 = w t − l r ⋅ m ^ t / V ^ t w_{t+1}=w_t-lr\cdot\hat m_t/\hat V_t wt+1=wt−lr⋅m^t/V^t
代码实现:
# 初始化
global_step = 0
vw, vb = 0, 0
mw, mb = 0, 0
betam = 0.9
betav = 0.999
...
for epoch in range(epoches): # 每一次epoch遍历一次数据集
Loss = 0
# lr = lr_base * lr_decay ** (epoch / lr_step)
for step, (x_train, y_train) in enumerate(data_train): # 每一个step遍历一个batch
global_step += 1
with tf.GradientTape() as tape:
...
grads = tape.gradient(loss, [w1, b1]) # 计算梯度
# Adam
mw = betam * mw + (1 - betam) * grads[0]
mb = betam * mb + (1 - betam) * grads[1]
vw = betav * vw + (1 - betav) * tf.square(grads[0])
vb = betav * vb + (1 - betav) * tf.square(grads[1])
m_w = mw / (1 - tf.pow(betam, int(global_step)))
m_b = mb / (1 - tf.pow(betam, int(global_step)))
v_w = vw / (1 - tf.pow(betav, int(global_step)))
v_b = vb / (1 - tf.pow(betav, int(global_step)))
w1.assign_sub(lr * m_w / tf.sqrt(v_w)) # 参数空间更新
b1.assign_sub(lr * m_b / tf.sqrt(v_b))
训练结果为:训练时间 t A d a m = 12.487653255462646 s t_{Adam}=12.487653255462646s tAdam=12.487653255462646s,两条曲线如图所示

3. 常用优化器比较
| 优化器 | 动量表达形式 | 训练时间 / s / s /s | 收敛速度 / e p o c h epoch epoch |
|---|---|---|---|
| S G D SGD SGD | m t = g t m_t=g_t mt=gt V t = 1 V_t=1 Vt=1 |
8.394366025924683 8.394366025924683 8.394366025924683 | ≈ 200 \approx200 ≈200 |
| S G D M SGDM SGDM ( β = 0.9 ) (\beta=0.9) (β=0.9) |
m t = β m t − 1 + ( 1 − β ) g t m_t=\beta m_{t-1}+(1-\beta)g_t mt=βmt−1+(1−β)gt V t = 1 V_t=1 Vt=1 |
9.672947883605957 9.672947883605957 9.672947883605957 | > 100 >100 >100 |
| A d a g r a d Adagrad Adagrad | m t = g t m_t=g_t mt=gt V t = ∑ τ = 1 t g τ 2 V_t=\sum_{\tau=1}^{t} g_\tau^2 Vt=∑τ=1tgτ2 |
9.278505802154541 9.278505802154541 9.278505802154541 | 60 − 70 60-70 60−70 |
| R M S P r o p RMSProp RMSProp ( β = 0.9 ) (\beta=0.9) (β=0.9) |
m t = g t m_t=g_t mt=gt V t = β V t − 1 + ( 1 − β ) g t 2 V_t=\beta V_{t-1}+(1-\beta)g_t^2 Vt=βVt−1+(1−β)gt2 |
9.854762315750122 9.854762315750122 9.854762315750122 | ≈ 40 \approx 40 ≈40(调小 l r lr lr后) (最终 A c c < 1.0 Acc<1.0 Acc<1.0) |
| A d a m Adam Adam ( β 1 = 0.9 (\beta_1=0.9 (β1=0.9 β 2 = 0.999 ) \beta_2=0.999) β2=0.999) |
m t = β 1 m t − 1 + ( 1 − β 1 ) g t m_t=\beta_1 m_{t-1}+(1-\beta_1)g_t mt=β1mt−1+(1−β1)gt 修正: m ^ t = m t / ( 1 − β 1 t ) \hat m_t=m_t/(1-\beta_1^t) m^t=mt/(1−β1t) V t = 1 β 2 V t − 1 + ( 1 − β 2 ) g t 2 V_t=1\beta_2 V_{t-1}+(1-\beta_2)g_t^2 Vt=1β2Vt−1+(1−β2)gt2 修正: V ^ t = V t / ( 1 − β 2 t ) \hat V_t=V_t/(1-\beta_2^t) V^t=Vt/(1−β2t) |
12.487653255462646 12.487653255462646 12.487653255462646 | 20 − 30 20-30 20−30 |
因此实际使用时,需要在训练时间(模型复杂度)和收敛速度(有时还需考虑训练精度)上寻求平衡