CRF模型详解
条件随机场(CRF)是自然语言处理中的基础模型, 广泛用于分词, 实体识别和词性标注等场景. 随着深度学习的普及, BILSTM+CRF, BERT+CRF, TRANSFORMER+CRF等模型, 逐步亮相, 并在这些标注场景, 效果有显著的提升.
下面是我学习CRF的学心总结, 看了多篇知乎, paper, 和CRF++的实现代码后, 终于有了深刻的理解.
基础概念
首先, 一起看一下随机过程, 随机场, 马尔可夫随机场的定义, 在最后请出条件随机场.
随机过程:
设 T T T是一无限实数集, 把依赖于参数 t ∈ T t\in T t∈T的一族(无限多个)随机变量称为随机过程, 记为 X ( t ) , t ∈ T {X(t), t \in T} X(t),t∈T
随机场: 从平面(随机过程)到向量空间(随机场)
若 T T T是 n n n维空间的某个子集, 即 t t t是一个 n n n维向量, 此时随机过程又称为随机场. 常见随机场有: 马尔可夫随机场(MRF), 吉布斯随机场(GRF), 条件随机场(CRF)和高斯随机场.
马尔可夫随机场:
具有马尔可夫性的随机场.
马尔可夫性: P ( Y v ∣ Y w , w ≠ v ) = P ( Y v ∣ Y w , w ∼ v ) P(Y_v|Y_w, w\neq v) = P(Y_v|Y_w, w \sim v) P(Yv∣Yw,w=v)=P(Yv∣Yw,w∼v)
- w ∼ v w \sim v w∼v表示在图 G = ( V , E ) G=(V, E) G=(V,E)中与顶点 v v v有边连接的所有顶点 w w w
- w ≠ v w \neq v w=v表示顶点 v v v以外的所有顶点
- Y v Y_v Yv与 Y w Y_w Yw为顶点 v v v与 w w w对应的随机变量
那么, 条件随机场是如何定义的呢?
条件随机场:
设 X X X与 Y Y Y是随机变量, P ( Y ∣ X ) P(Y|X) P(Y∣X)是在给定 X X X的条件下 Y Y Y的条件概率分布.
若随机变量 Y Y Y构成一个由无向图 G = ( V , E ) G=(V, E) G=(V,E)表示的马尔可夫随机场, 即
P ( Y v ∣ X , Y w , w ≠ v ) = P ( Y v ∣ X , Y w , w ∼ v ) P(Y_v|X, Y_w, w \neq v) = P(Y_v|X, Y_w, w \sim v) P(Yv∣X,Yw,w=v)=P(Yv∣X,Yw,w∼v)
对任意顶点 v v v成立, 则称条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)为条件随机场.
- w ∼ v w \sim v w∼v表示在图 G = ( V , E ) G=(V, E) G=(V,E)中与顶点 v v v有边连接的所有顶点 w w w
- w ≠ v w \neq v w=v表示顶点 v v v以外的所有顶点
- Y v Y_v Yv与 Y w Y_w Yw为顶点 v v v与 w w w对应的随机变量
只基于Y序列做预测, 太单调了, 所以额外给出一个观测序列X, 帮助你更好的做决策. 这就是从马尔可夫随机场变成条件随机场的过程. 条件随机场中, "条件"指的是给定观测序列X的情况, 求状态序列Y的概率, 即输出的是条件概率分布. 而"随机场"指的是状态序列Y构成的随机场.
线性链条件随机场:
常见的标注场景, 如分词, 实体识别和词性标注等, 都是典型的线性链条件随机场. 那么什么是线性链条件随机场呢?
X X X和 Y Y Y有相同结构(线性表示的随机变量序列)的条件随机场就构成了线性链条件随机场. (这里指的线性, 指语言天然具有的先后顺序,成线性特性.)
定义:
设 X = ( X 1 , X 2 , . . . , X n ) X=(X_1, X_2, ..., X_n) X=(X1,X2,...,Xn), Y = ( Y 1 , Y 2 , . . . , Y n ) Y=(Y_1, Y_2, ..., Y_n) Y=(Y1,Y2,...,Yn)均为线性表示的随机变量序列,
若在给定随机变量序列 X X X的条件下,
随机变量序列 Y Y Y的条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)构成条件随机场, 即满足马尔可夫性
P ( Y i ∣ X , Y 1 , . . . , Y i − 1 , Y i + 1 , . . . , Y n ) = P ( Y i ∣ X , Y i − 1 , Y i + 1 ) P(Y_i|X, Y_1, ..., Y_{i-1}, Y_{i+1}, ..., Y_n) = P(Y_i|X, Y_{i-1}, Y_{i+1}) P(Yi∣X,Y1,...,Yi−1,Yi+1,...,Yn)=P(Yi∣X,Yi−1,Yi+1)
则称 P ( Y ∣ X ) P(Y|X) P(Y∣X)为线性链条件随机场. 其中 i = ( 1 , 2 , . . n ) i=(1,2,..n) i=(1,2,..n), 在 i = 1 i=1 i=1和 i = n i=n i=n时只考虑单边.
两种主要的线性链条件随机场的图结构如下:
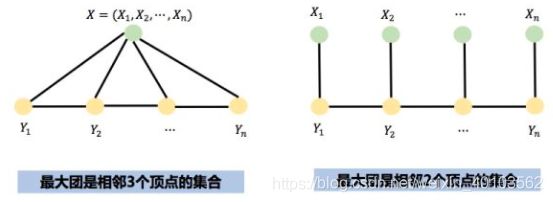
由于线性链条件随机场应用非常广泛, 所以习惯把"线性链条件随机场"简称为条件随机场(CRF).
CRF公式
根据Hammersley Clifford定理, 一个无向图模型的概率, 可以表示为定义在图上所有最大团上的势函数的乘积.
那么, CRF的条件概率可以在因子分解下表示为:

线性链CRF的因子分解

如上图, 线性链CRF的因子分解, 根据函数类型, 可细化为:
P ( y ∣ x ) = 1 Z ( x ) exp ( ∑ i , k λ k t k ( y i − 1 , y i , x , i ) + ∑ i , l μ l s l ( y i , x , i ) ) P(y|x) = \frac{1}{Z(x)} \exp (\sum_{i,k}\lambda_k t_k(y_{i-1}, y_i, x, i) + \sum_{i, l}\mu_l s_l (y_i, x, i)) P(y∣x)=Z(x)1exp(∑i,kλktk(yi−1,yi,x,i)+∑i,lμlsl(yi,x,i))
其中,
Z ( x ) = ∑ y exp ( ∑ i , k λ k t k ( y i − 1 , y i , x , i ) + ∑ i , l μ l s l ( y i , x , i ) ) Z(x) = \sum_y \exp (\sum_{i,k}\lambda_k t_k(y_{i-1}, y_i, x, i) + \sum_{i,l}\mu_l s_l(y_i, x, i)) Z(x)=∑yexp(∑i,kλktk(yi−1,yi,x,i)+∑i,lμlsl(yi,x,i))
- t k t_k tk为转移特征函数, 在CRF++中转移特征由Bigram Template + 输入字(词)序列生成
- s l s_l sl为状态特征函数, 在CRF++中状态特征由Uigram Template + 输入字(词)序列生成
CRF中, 通常有两类特征函数, 分别为转移特征和状态特征. 状态特征表示输入序列与当前状态之间的关系. 转移特征表示前一个输出状态与当前输出状态之间的关系. CRF++中, 特征模板需要人工设定, 有一定的局限性. 若结合深度神经网络, 如BERT+CRF, 则特征就可由模型自动学习得到, 具体讲, BERT学习状态特征, CRF学习转移特征, 并用viterbi获取最优路径.
理论讲了很多, 接下来讲讲CRF的实现代码, 以牛逼的CRF++为例.
CRF++实现详解
https://taku910.github.io/crfpp/ 是开源的CRF++的工具源代码.
CRF++中, 核心功能分为模型训练和预测两部分.
模型训练
整个训练过程分为三步:
- 准备训练数据集
- 通过定义特征模板, 自动生成特征函数集
- 通过LBFGS算法, 学习特征函数的权重
训练数据集
训练数据集, 按照文档要求准备即可, 例子如下:
山 B_PROV
东 I_PROV
省 I_PROV
菏 B_CITY
泽 I_CITY
市 I_CITY
牡 B_DIST
丹 I_DIST
区 I_DIST
重 B_ROAD
庆 I_ROAD
路 I_ROAD
特征函数定义
特征模板格式:%x[row,col]。x可取U或B,对应两种类型。方括号里的编号用于标定特征来源,row表示相对当前位置的行,0即是当前行;col对应训练文件中的列。这里只使用第1列(编号0),即文字。若值为1, 则使用标签值.
定义特征模板:
# Unigram
U00:%x[-2,0]
U01:%x[-1,0]
U02:%x[0,0]
U03:%x[1,0]
U04:%x[2,0]
U05:%x[-2,0]/%x[-1,0]/%x[0,0]
U06:%x[-1,0]/%x[0,0]/%x[1,0]
U07:%x[0,0]/%x[1,0]/%x[2,0]
U08:%x[-1,0]/%x[0,0]
U09:%x[0,0]/%x[1,0]
# Bigram
B
特征函数, 前面提到过, 分为两种, 转移特征和状态特征. 特征模板中的Unigram or Bigram, 是针对输出序列 Y Y Y, 即标注label而言的. 如转移特征 t k ( y i − 1 , y i , x , i ) t_k(y_{i-1}, y_i, x, i) tk(yi−1,yi,x,i), 涉及到 y i − 1 y_{i-1} yi−1和 y i y_i yi, 所以叫Bigram特征. 状态特征 s l ( y i , x , i ) s_l(y_i, x, i) sl(yi,x,i)只涉及到 y i y_i yi, 所以叫Unigram特征.
以训练集中的第一行为例, 基于上面的特征模板, 生成10个特征 (此时还未与label进行结合):
U00:%x[-2, 0] =>“U00:_B-2” (这里的_B-2指的是beginning of sentence)
U01:%x[-1, 0] => “U01:_B-1” (_B-1, _B-2均为指代)
U02:%x[0, 0] => “U02:山”
U05:%x[-2,0]/%x[-1,0]/%x[0,0] => “U05:_B-2/_B-1/山”
U06:%x[-1,0]/%x[0,0]/%x[1,0] => “U06:_B-1/山/东”
U07:%x[0,0]/%x[1,0]/%x[2,0] => “U07:山/东/省”
U08:%x[-1,0]/%x[0,0] => “U08:_B-1/山”
U09:%x[0,0]/%x[1,0] => “U09:山/东”
基于输入序列生成的单边特征, 再与标签集合(Y集合)结合, 生成最终的特征函数.
若特征类型为Unigram, 每行模板生成一组状态特征函数,数量是L*N 个,L是标签状态数。N是此行模板在训练集上展开后的去重后的样本数, 如:
func0 = if (output = B_PROV and feature=“U02:山”) return 1 else return 0
func1 = if (output = I_PROV and feature=“U02:山”) return 1 else return 0
func1 = if (output = B_CITY and feature=“U02:山”) return 1 else return 0
…
若特征类型为Bigram, 每行模板生成一组转移特征函数, 数量是L*L*N 个。经过训练后,这些函数的权值反映了上一个节点的标签对当前节点的影响。例如对应 B00:%x[0, 0]:
func0 = if (prev_output = B_PROV and output = B_PROV and feature=“U02:山”) return 1 else return 0
func1 = if (prev_output = B_PROV and output = I_PROV and feature=“U02:山”) return 1 else return 0
func2 = if (prev_output = B_PROV and output = B_CITY and feature=“U02:山”) return 1 else return 0
…
funcN = if (prev_output = I_DIST and output = B_PROV and feature=“U02:山”) return 1 else return 0
…
现实中, 若Bigram模板的定义中, 涉及输入序列, 容易导致特征数巨大, 所以默认只使用简单的B, 即简化的转移特征函数 t k ( y i − 1 , y i ) t_k(y_{i-1}, y_i) tk(yi−1,yi), 与输入序列无关.