目录
- C1 Introduction to Statistical Learning
- 1.1Statistical Learning介绍:
- 1.1.1 估计 \(f\) 的目的:prediction和/或inference。
- 1.1.2 估计 \(f\) 的方法:parametric 或 non-parametric
- 1.2 评估模型准确性
- 1.2.1 回归的评估
- 1.2.2 Bias-Variance的平衡
- 1.2.3 分类的情况
- 1.1Statistical Learning介绍:
- C2 Linear Regression
- 2.1 简单线性回归
- 2.1.1 评估系数的准确性
- 2.1.2 评估模型的准确性
- 2.2 多元线性回归
- 2.2.2 一些重要问题
- 2.3 回归模型的其他思考
- 2.3.1 Qualitative Predictors
- 2.3.2 线性模型的拓展
- 2.3.3 Potential Problems
- 3.5 线性回归和KNN的比较
- 2.1 简单线性回归
- C3 Classification
- 3.1 总体介绍
- 3.2 逻辑回归
- 3.2.1模型
- 3.2.2模型计算和预测
- 3.3 Linear Discriminant Analysis
- 3.3.1 LDA计算
- 3.3.2 QDA计算
- 3.4 比较分类方法
- 3.5 Lab
- C4 Resampling Methods
- 4.1 Cross-Validation
- 4.2 The Bootstrap
- C5 Linear Model Selection and Regularization
- 5.1 Subset Selection
- 5.2 Shrinkage Methods
- 5.3 Dimension Reduction Methods
- 5.3.1 PCA
- 5.3.2 PLS
- 5.4 思考高维数据
- 5.5 Lab
- C6 非线性模型
- 6.1模型介绍
- 6.1.1 Basis Functions
- 6.1.2 Regression Splines
- 6.1.3 Smoothing Splines
- 6.1.4 Local Regression
- 6.1.5 Generalized Additive Models
- C7 Tree-Based Methods
- 7.1 决策树基础
- 7.2 Bagging, Random Forests, Boosting
- C8 SVM
- 8.1 Maximal Margin Classifier
- 8.2 Support Vector Classifiers(soft margin classifier)
- 8.3 Support Vector Machines
- 8.4 Lab
- C9 Unsupervised Learning
- 9.1 Clustering Methods
C1 Introduction to Statistical Learning
1.1Statistical Learning介绍:
1.Statistical learning
a vast set of tools ( supervised or unsupervised ) for estimating Model. supervised 为了预测,unsupervised 为了发现。
2.variables
input variables: predictors, independent variables, features, or sometimes just variables
output variables: response or dependent variable
3.\(Y =f(X)+\epsilon\)
Here f is some fixed but unknown function of \(X_1\), . . . , \(X_p\), and ε is a random error term, which is independent of \(X\) and has mean zero. 由于 \(\epsilon\) 代表了所有的错误,如模型形式错误,遗漏重要predictors,测量错误等,所以假设其实难以保证。
4.权衡 Accuracy 和 Interpretability
5.supervised, unsupervised and semi-supervised
6.Regression Versus Classification
1.1.1 估计 \(f\) 的目的:prediction和/或inference。
1.prediction
(1)\(\hat{Y} = \hat{f}(X)\) where \(\hat{f}\) represents our estimate for \(f\) , and \(\hat{Y}\) represents the resulting prediction for \(Y\). \(\hat{f}\) is often treated as a black box. 只要预测准就行,不关心模型的形式。
(2)reducible error (\(f\)) and the irreducible error (\(ε\)):下面式子在\(\hat{f}\)和\(X\)固定的情况下得出
\[ \begin{align} E(Y −\hat{Y})^2 &= E[f(X)+ε−\hat{f}(X)]^2\\ & = \underbrace{[f(X)−\hat{f}(X)]^2}_{Reducible} + \underbrace{Var(ε)}_{Irreducible}\\ \end{align} \]
目标是减少reducible error,而irreducible error为模型的准确度设置了我们无法知道的上限。
2.inference
understand how \(Y\) changes as a function of \(X_1\), . . . , \(X_p\) ,需要知道模型的形式
目的是知道哪些predictors与response显著相关;response和每一个predictor的关系;模型是否能线性解释
根据估计 \(f\) 的目的选择相应的模型。
1.1.2 估计 \(f\) 的方法:parametric 或 non-parametric
1.parametric(model-based approach)
步骤:假设 functional form, or shape, of $ f$ (eg. linear), then use the training data to fit or train the model
特点:将估计整个 \(f\) 变为估计参数,问题对模型估计不够准确。选择flexible模型的话能提高准确,但可能overfitting
2.Non-parametric
步骤:不假设 functional form,直接训练模型
特点:没有简化问题,提高对模型估计的准确性,但需要更多训练数据
1.2 评估模型准确性
1.2.1 回归的评估
以mean squared error (MSE) 为例,假设真正的 \(f\) 是下左图的黑线,处于某个适中的flexibility,模型的flexibility从最小值开始,test set远大于training set,则随着flexibility的增加,train MSE会不断减少,test MSE会先减少后增加,最小值最接近\(Var(ε)\)。
上图橙和绿分别代表underfitting和overfitting。由于training set不够大,overfitting使得模型发现了并不存在于test set的规律(noise部分)。
1.2.2 Bias-Variance的平衡
test MSE的期望可分解如下:
\[ E(y_0 − \hat{f}(x_0))^2 = Var(\hat{f}(x_0)) + [Bias(\hat{f}(x_0))]^2 + Var(ε). \]
所以,为了最小化expected test MSE,需要减少variance and bias。
前者表示利用不同training set评估模型时产生的差异。一般情况下,越flexible的模型,variance越大(如1.2.1右图中,绿色模型的test set和training set的MSE的差距很大,橙色很小)
后者表示模型拟合不足
正如1.2.1右图中的test MSE,随着flexibility的增加,variance / bias先减少后增加。
1.2.3 分类的情况
error rate
1.The Bayes Classifier
基于predictor值,将每一个observation推测为最有可能的class。即使得 $\mathrm{Pr}(Y = j | X = x_0) $ 这个概率最大。例如,在binary classification问题上,如果 \(\mathrm{Pr}(Y = 1\ |\ X = x_0) > 0.5\) 则预测class one,否则预测class two。
Bayes Classifier 可以产生 lowest possible test error rate, Bayes error rate: \(1−E( \mathrm{max}_j\mathrm{Pr}(Y =j|X) )\)
2.K-Nearest Neighbors (注意要scale)
在现实中,由于无法得知在 \(X\) 条件下 \(Y\) 的分布,所以无法计算Bayes Classifier。而KNN classifier 是一个很接近Bayes Classifier的方法。
\[ \mathrm{Pr}(Y =j\ |\ X=x_0)=\frac{1}{K}\sum_{i\in N_0}{I(y_i=j)} \]
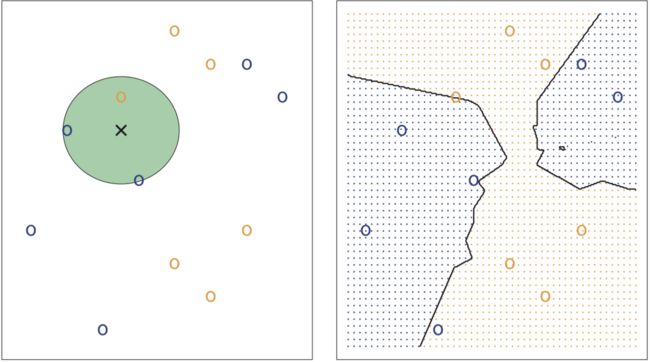
如下左图所示,假设K=3,蓝色和橙色圈分别代表class 1和class 2,交叉为 \(x_0\) ,这里使得Pr最大的是j = class 1。右图为K=3时的贝叶斯边界。
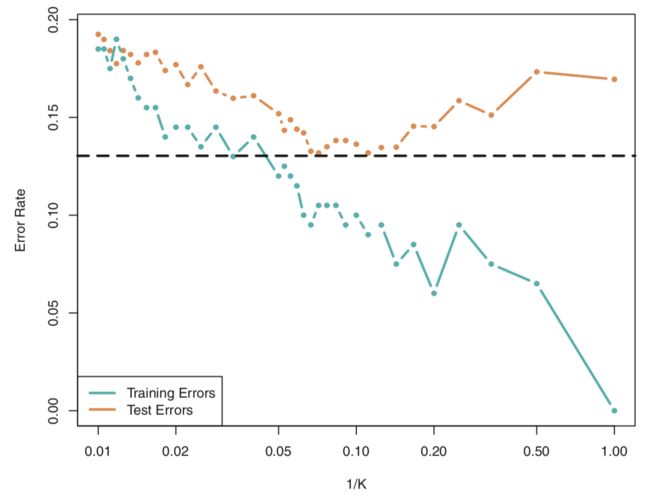
KNN Classifier 和 Bayes Classifier的接近程度部分取决于K的选择,K越小,flexibility越大,反之越小。和回归情况一样,当K=1时会overfitting,training error rate等于0,但test error rate很高。
C2 Linear Regression
本章利用Advertising数据,如下所示,三个媒体的数值为广告投入费用:
| row_id | TV | Radio | Newspaper | Sales |
|---|---|---|---|---|
| 0 | 230.1 | 37.8 | 69.2 | 22.1 |
要回答的问题:
- Sales和广告投入是否有关系:多元回归 + F-statistics
- 关系有多大:RES/mean_response or R^2^
- 哪些媒体跟sales有关系:t-statistics or p-value
- 每个媒体的单位投入对应多少sales的变化,多准确:\(\hat{\beta_j}\) 的置信区间
- 如何准确预测:prediction interval(预测individual response)或confidence intervals(预测average response)
- 关系是否为线性:residual plots
2.1 简单线性回归
$Y ≈ β_0 + β_1X $ 表示regressing Y on X (or Y onto X)
\(\hat{y} = \hat{β}_0 + \hat{β}_1 x\) least squares line, where \(\hat{y}\) indicates a prediction of \(Y\) on the basis of \(X = x\). 目的是让 \(y_i ≈ \hat{y}_i\) ,而从全部数据来看,就是要最小化RSS。
\(\mathrm{RSS} = e^2_1 + e^2_2 + · · · + e^2_n\) residual sum of squares,其中\(e_i =y_i - \hat{y}_i\)
通过计算 \(\hat{β}_0\) 和 \(\hat{β}_1\) 使得RSS取最小值。
#计算,进行中心化,但不标准化;reshape(-1,1)就是把X变为n*1的形状,由于n不知道,可用-1让python自己算
X = scale(advertising.TV, with_mean=False, with_std=False).reshape(-1,1)
y = advertising.Sales
regr = skl_lm.LinearRegression()
regr.fit(X,y)
print(regr.intercept_) #7.032593549127693
print(regr.coef_) #[0.04753664]
#画图,order表示flexibility,ci表示置信水平[0,100](数据量大时建议None),s表示点的大小
sns.regplot(advertising.TV, advertising.Sales, order=1, ci=None, scatter_kws={'color':'r', 's':9})
plt.xlim(-10,310)
plt.ylim(ymin=0)population regression line: $Y = β_0 + β_1X + ε $ 假设Y和X是线性关系,该线是最好的线性回归。下图的红线代表population regression line,各点就是根据它加上一个 ε(服从正态分布)得出的,而蓝线是上面提到的least squares line,即通过那些数据点估计出的线。
由于根据特定的数据集来推断,所以难免会有bias。但在模型设定正确的情况下,通过大量数据,所推断出的least squares line会十分接近 population regression line,会是unbiased。如上右图所示,如果平均各线,结果不会与真线相差太大。
2.1.1 评估系数的准确性
估计值与真实值的平均差异(标准差,但无法知道多小才算小);在某个置信水平下,系数值的范围是多少(置信区间);关系是否显著(null hypothesis)。
1.类比“利用sample mean估计population mean的准确性”:
$\mathrm{Var}(\hat{μ}) = \mathrm{SE}(\hat{μ})^2 = \frac{\sigma^2}{n} $ where σ is the standard deviation of each of the realizations \(y_i\) of Y,要求n个观测值各不相关。
the standard error \(\mathrm{SE}(\hat{μ})\) 表示估计值与真实值的平均差异,当n越大,差异越小,即估计值越准确。
2.类似的,系数的式子如下:
\(\mathrm{SE}(\hat{β}_0)^2 =σ^2[\frac{1}{n}+\frac{\bar{x}^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2}]\) , \(\mathrm{SE}(\hat{β}_1)^2 =\frac{\sigma^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2}\) 其中\(σ^2 = \mathrm{Var}(ε)\) 。这两个式子严格成立的话,\(\epsilon_i\) 和 \(\sigma^2\) 是uncorrelated的。虽然这规定不符合,但是结果还是可以接受的。从式子可以知道,如果x很分散,那么需要更关注斜率;如果x的均值等于0,那么 \(\hat{β}_0 = \bar{y}\) 。通常来说,\(\sigma\) 是要通过样本推断的,式子为 \(\mathrm{RSE} = \sqrt{\mathrm{RSS}/(n − 2)}\) residual standard error
利用标准差可以计算置信区间。例如 \(\hat{β}_1\) 的置信区间为\(\hat{β}_1±2·\mathrm{SE}(\hat{β_1})\) ,意思大概是通过100次样本估计,有95次这些区间包含了未知的真值。这个式子假设error为高斯分布,而2会随n的变化而变化,更加准确应该用t分布。
上面回归的系数,在95%置信水平下,区间为 \(β_0\) [6.130, 7.935] 和 \(β_1\) [0.042, 0.053] 。在没有广告的情况下,sales的范围是[6.130, 7.935],而每增加一单位的电视广告投入,sales增加的范围是[0.042, 0.053]。
利用标准差还可以进行假设检验,例如下面是针对 \(\hat{\beta_1}\) 的null hypothesis:\(H_0: \beta_1=0\) , \(t=\frac{\hat{\beta_1}-0}{\mathrm{SE}(\hat{\beta}_1)}\) 。从式子可以看出,如果系数值越大,且它的标准差越小,那么该系数就越不可能为0,即该系数的predictors跟response的关系大且显著。或者说p值越小(拒绝原假设),关系越显著。
import statsmodels.formula.api as smf
est = smf.ols('Sales ~ TV', advertising).fit()
est.summary().tables[1]| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 7.0326 | 0.458 | 15.360 | 0.000 | 6.130 | 7.935 |
| TV | 0.0475 | 0.003 | 17.668 | 0.000 | 0.042 | 0.053 |
2.1.2 评估模型的准确性
指标为the residual standard error (RSE) 和 the R2
# RSE的计算
import math
n = advertising.TV.count()
rss = ((advertising.Sales - est.predict())**2).sum()
rse = math.sqrt(rss/(n-2)) # 3.26
#R2和F-test
est.summary().tables[0] # R2 0.612, F-test 312.11.RSE测量模型the lack of fit部分
RSE=3.26意味着sales有3.26的波动,大小可通过RSE/(sales mean)判断,此数据结果为23%。
2.R^2^
式子为 $1− \frac{\mathrm{RSS}}{\mathrm{TSS}} $ ,它是一个测量X和Y线性关系的指标。在复杂的问题里,R^2^小于0.1也是很正常的。当单变量进行线性回归时,R^2^是等于Cor^2^(X, Y)的,但后者不适用于多变量。
2.2 多元线性回归
简单线性回归当中,如果不同回归中的predictors是相关的,这会产生误导。
当把TV,Radio,Newspaper三个predictors合在一起回归\(\hat{y} = \hat{β}_0 + \hat{β}_1x_1 + \hat{β}_2x_2 + \hat{β}_3x_3\),结果如下
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 2.9389 | 0.312 | 9.422 | 0.000 | 2.324 | 3.554 |
| TV | 0.0458 | 0.001 | 32.809 | 0.000 | 0.043 | 0.049 |
| Radio | 0.1885 | 0.009 | 21.893 | 0.000 | 0.172 | 0.206 |
| Newspaper | -0.0010 | 0.006 | -0.177 | 0.860 | -0.013 | 0.011 |
此处Newspaper并不明显,但实际上,在简单回归当中,Newspaper还是相当显著的,但在多元线性回归中却不显著。通过分析下面的相关系数我们可以发现,Newspaper和Radio的相关性是挺大的。这反映了,如果在某个市场通过Radio投放广告,我们会习惯同时增加一些Newspaper广告的投放,所以归根到底其实是Radio的影响。sales,radio和newspaper三者的关系类似于shark_attack,temperature和ice-cream_sales。当引入真正重要的变量(radio或temperature)时,另一个与之相关的变量(newspaper或ice-cream_sales)就会不再显著了。
| TV | Radio | Newspaper | Sales | |
|---|---|---|---|---|
| TV | 1.000000 | 0.054809 | 0.056648 | 0.782224 |
| Radio | 0.054809 | 1.000000 | 0.354104 | 0.576223 |
| Newspaper | 0.056648 | 0.354104 | 1.000000 | 0.228299 |
| Sales | 0.782224 | 0.576223 | 0.228299 | 1.000000 |
#计算结果
est = smf.ols('Sales ~ TV + Radio + Newspaper', advertising).fit()
est.summary().table[1]
#相关系数
advertising.corr()2.2.2 一些重要问题
1.response和predictors是否相关?
F-test: $H_0 :β_1 =β_2 =···=β_p =0 $ , \(F=\frac{(\mathrm{TSS-RSS)}/p}{\mathrm{RSS}/(n-p-1)}\) 。当H~0~ 为真时,分子等于 \(\sigma^2\) ,而分母的期望就是等于 \(\sigma^2\) ,所以此时F接近1。否则,分子会大于 \(\sigma^2\) ,F也就大于1。但是否拒绝H~0~取决于n和p,当n足够大,F-statistic会服从F分布,然后查表的结果,但最方便的方法是通过软件看p值。
另一种F-test: $H_0 : β_{p−q+1} =β_{p−q+2} =...=β_p =0 $ , \(F=\frac{(\mathrm{RSS_0-RSS)}/q}{\mathrm{RSS}/(n-p-1)}\) 。判断某predictors子集(q个元素)是否与response有关。RSS~0~是去掉q个predictors后回归并计算RSS得到的。在极端情况下,即q=1时,F-statistics相当于(t-statistics)^2^ 。但通过t-statistics来判断整个模型的显著性是有很大风险的,因为每个t-statistics都是有一定置信水平。例如有5%错过真值,当t检验次数一多,就很难保证全部检验都不会错过真值。
2.变量选择(C5详细讲)
Forward selection:从简单回归开始,选择一个对减少RSS效果最好的变量,然后在一元回归基础上选择下一个效果最大的变量……该策略问题:可能一开始引入一些后来变得不显著的变量。
Backward selection:先减去p值最大的变量,直到所有变量的p值都很小。
Mixed selection:按照Forward开始,当加入新变量使得之前的某个变量p值不显著时,去掉不显著的……直到所有模型中的变量的p值很低,模型外的变量一加进来该变量的p值就很大。
3.模型拟合
RSE and R^2^,后者在多元回归中等于 $\mathrm{Cor}(Y, \hat{Y})^2 $ 。就目前而言,看RSE比较好,能防止加入太多无关变量。另外,通过比较不同变量值情况下,模型是倾向于高估还是低估还能发现模型是否有忽略多变量交互作用的情况。
4.预测
目前有三个不确定性:
least squares plane \(\hat{Y}\) 和 population regression plane \(f(X)\) (注意这个不含 \(\epsilon\) )的差别用confidence interval衡量。例如95%的置信区间表示这些区间有95%是包含真值的。
模型bias
irreducible error
prediction intervals包含上面三种不确定性,例如95%的预测区间表示这些区间有95%包含某特定 x 对应的 y。自然,这个区间比置信区间大不少。
2.3 回归模型的其他思考
2.3.1 Qualitative Predictors
two levels predictors:
下面是 \(x_i\) (indicator or dummy variable)为0/1编码(也可以1/-1编码,不同方式只影响解释,不影响结果)
\[ y_i = β_0 + β_1x_i + \epsilon_i =\left\{ \begin{array}\\ β_0 + β_1 + \epsilon_i &\mathrm{if\ ith\ person\ is\ female} \\ β_0 + \epsilon_i &\mathrm{if\ ith\ person\ is\ male} \end{array} \right. \]
$β_0 $ 作为male的平均值,\(β_0 + β_1\)为female的均值,\(β_1\)就是均值差异。第二个式子没有dummy variable成为baseline。
2.3.2 线性模型的拓展
标准线性回归有两个重要假设:additive和linear。前者表示不同的predictors对response的影响是独立的,后者表示predictors一单位的变化对response的影响是constant的。
去除additive假设
additive假设限制了interaction效应,比如本章节数据中,TV和radio的广告投入可能会相互促进sales。换句话说,向TV和radio分别投入0.5比只向TV或者radio单独投入1效果要好。下面公式解除了additive假设:
\(Y = β_0 + β_1X_1 + β_2X_2 + β_3X_1X_2 + \epsilon\) ,其中 \(X_1X_2\) 称为交互项
上式中,其中一个predictor的变化,对response的影响不再是固定的(如果另一个predictor也变化)。再次回归的结果如下:
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 6.7502 | 0.248 | 27.233 | 0.000 | 6.261 | 7.239 |
| TV | 0.0191 | 0.002 | 12.699 | 0.000 | 0.016 | 0.022 |
| Radio | 0.0289 | 0.009 | 3.241 | 0.001 | 0.011 | 0.046 |
| TV:Radio | 0.0011 | 5.24e-05 | 20.727 | 0.000 | 0.001 | 0.001 |
另外,R^2^由原来的89.7%上升到了96.8%,这表示交互项解释了之前模型RSS的(96.8 - 89.7)/(100 - 89.7) = 69 % 。根据hierarchical principle,如果引入了交互项,那么组成它的每个变量都要引入模型中,不管这些变量是否显著。
在qualitative情况下,additive
\[ balance_i ≈ β_0 + β_1\mathrm{income}_i +\left\{ \begin{array}\\ β_2 &\mathrm{if\ ith\ person\ is\ student} \\ 0 &\mathrm{if\ ith\ person\ is\ not \ student} \end{array} \right. \]
non-additive
\[ balance_i ≈ β_0 + β_1\mathrm{income}_i +\left\{ \begin{array}\\ β_2 + β_3 × \mathrm{income}_i &\mathrm{if\ ith\ person\ is\ student} \\ 0 &\mathrm{if\ ith\ person\ is\ not \ student} \end{array} \right. \]
非线性(多项回归)
\(Y = β_0 + β_1X_1 + β_2X_1^2 + \epsilon\) ,这是一个非线性函数,但仍是线性模型,所以在软件里的回归方式一样。
2.3.3 Potential Problems
1.response-predictor 非线性相关
在多元回归时,通过residual plot,即 \(e_i\) 和 \(\hat{y}_i\) 的散点图,可以发现模型是否为non-linearity。正常情况下,散点图是没有discernible pattern的,比如U型。如果有,则数据有非线性联系,可以对predictors进行非线性转换,如开方,平方等。
2.error项的相关性
线性模型假设他们不相关,但如果相关,那么模型真实的置信水平会更低,结果是95%的confidence and prediction intervals实际上并没有这么高,要把区间扩大才能达到95%。另外,也会高估parameter的显著性。
相关的情况通常出现在时间序列数据,可以通过计算 e 和 time_id 的相关系数。而非时间序列中,比如height onto weight,如果一些人是来自相同家庭,或有相同的饮食习惯,或生活在相同的环境,这些因素都会破坏error的独立性。
3.非固定方差的error项
如果 \(\mathrm{Var}(\epsilon_i) = σ^2\) 不成立,这会影响SE, confidence intervals 和 hypothesis tests。现实中经常不成立,比如在Residual plots中,rss的绝对值会随response的增大而增大(漏斗状)。解决这一问题可以通过对response进行转换,如 \(log Y\) 或 $\sqrt{Y} $ 。另一种情况是,\(i\)th response是 \(n_i\) 个观察值的均值,而这些观察值和 \(σ^2\) 不相关,那么\(i\)th response的方差为 \(σ_i^2 = σ^2/n_i\) ,利用weighted least squares修正,此处乘上\(n_i\)
4.Outliers
outlier(下面20号): \(y_i\) 的值和预测值相差很大很大。即使outlier不对回归的结果造成大影响,它也会影响增大RSE和降低R^2^。Studentized residuals plots可以identify outlier,当Studentized residuals超过±3时为outliers。这是适用于收集数据时出错产生的异常,但模型本身的缺陷,如缺失predictor也会出现outlier。
5.High Leverage Points
High Leverage Points(上面41号)比outliers严重,会大程度地影响拟合。通过计算leverage statistic来判断,值介于1/n 和 1,所有observations的平均杠杆为(p + 1)/n,如果远离该值,就很可能是High Leverage Points。
6.共线性
会降低回归系数的准确性,导致SE(\(\hat{\beta}_j\))增加,t-statistic降低,从而错误地放弃一些重要变量。通过correlation matrix可以发现共线性,但如果是多重共线性,则要计算variance inflation factor (VIF) 。该因子最小值为1,表示完全没有共线性,一般超过5或10才是有问题。解决方法是删除一个或者利用共线变量构造一个新变量。
#计算三个变量age, rating, and limit各自的VIF
est_Age = smf.ols('Age ~ Rating + Limit', credit).fit()
est_Rating = smf.ols('Rating ~ Age + Limit', credit).fit()
est_Limit = smf.ols('Limit ~ Age + Rating', credit).fit()
print(1/(1-est_Age.rsquared))
print(1/(1-est_Rating.rsquared))
print(1/(1-est_Limit.rsquared))3.5 线性回归和KNN的比较
两者的选择一般由数据的线性程度来决定。然而,当predictor较多时,即便是非线性数据,线性回归依然会比KNN好,这是由于curse of dimensionality。当数据是高维度时,non-parametric需要更多的样本来拟合。
C3 Classification
3.1 总体介绍
本章节default数据是经过改造的,实际数据不会这么理想。
df['default2'] = df.default.factorize()[0] #[0]为标签数组[1,0,0,0,1...],[1]为unique values数组,Index(['No', 'Yes'], dtype='object')
df['student2'] = df.student.factorize()[0]| default | student | balance | income | default2 | student2 | |
|---|---|---|---|---|---|---|
| 1 | No | No | 729.526495 | 44361.625074 | 0 | 0 |
| 2 | No | Yes | 817.180407 | 12106.134700 | 0 | 1 |
fig = plt.figure(figsize=(12,4)) # 整个结果框的大小
gs = mpl.gridspec.GridSpec(1, 4) # 对上面的框进行划分,这里是1行4列
ax1 = plt.subplot(gs[0,:-2]) # 占第一行直到倒数第二列(不包含)的位置
ax2 = plt.subplot(gs[0,-2])
ax3 = plt.subplot(gs[0,-1])
df_no = df[df.default2 == 0].sample(frac=0.15) # 从没有违约records中抽样
df_yes = df[df.default2 == 1]
df_ = df_no.append(df_yes)
ax1.scatter(df_[df_.default == 'Yes'].balance, df_[df_.default == 'Yes'].income, s=40, c='orange', marker='+',
linewidths=1)
ax1.scatter(df_[df_.default == 'No'].balance, df_[df_.default == 'No'].income, s=40, marker='o', linewidths='1',
edgecolors='lightblue', facecolors='white', alpha=.6)
ax1.set_ylim(ymin=0)
ax1.set_ylabel('Income')
ax1.set_xlim(xmin=-100)
ax1.set_xlabel('Balance')
c_palette = {'No':'lightblue', 'Yes':'orange'}
sns.boxplot('default', 'balance', data=df, orient='v', ax=ax2, palette=c_palette)
sns.boxplot('default', 'income', data=df, orient='v', ax=ax3, palette=c_palette)
gs.tight_layout(plt.gcf()) # 调整每张图的距离线性回归最多适用于binary分类问题,但最好把prediction限制成probability,如下面的Logistic Regression。更多的类别在线性回归中会出现无意义的ordering。
3.2 逻辑回归
3.2.1模型
把回归值限制在0~1。下面log叫做log odds
\[ p(X) = \frac{e^{\beta_0+\beta_1X}}{1+e^{\beta_0+\beta_1X}}\ \ \ \ \ \rightleftharpoons \ \ \ \ \ log(\frac{p(X)}{1-p(X)})=\beta_0+\beta_1X \]
X和p(X)的关系是非直线的,其中一个变量的变化对另一个的影响取决于该变量的当前值。
该模型一般用maximum likelihood来估计,最小二乘法是它的一个特例。这个方法的目的是寻找最优参数组合,使得当default时, \(\hat{p}(x_i)\) 值接近1,反之接近0。公式表达如下,maximize这个likelihood function:
\[ \ell(β_0,β_1) = \prod_{i:y_i=1}p(x_i)\prod_{{i^{'}:y_{i^{'}}=0}}(1-p(x_{i^{'}})) \]
3.2.2模型计算和预测
y = df.default2.ravel() # ravel把series变为ndarray,不调用也可以
x = sm.add_constant(df.balance) # 给df.balance加上一列constant,值为1,返回DF
mult_x = sm.add_constant(df[['balance', 'income', 'student2']])
est = smf.Logit(y, x).fit()
est.summary2().tables[1] # 逻辑回归要用summary2
est.predict([1,2000]) #0.5858 参数里的顺序与上面x一样,先constant
#sklearn
clf = skl_lm.LogisticRegression(solver='newton-cg')
x = df.balance.values.reshape(-1,1)
clf.fit(x,y) #可接受series| Coef. | Std.Err. | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | -10.651331 | 0.361169 | -29.491287 | 3.723665e-191 | -11.359208 | -9.943453 |
| balance | 0.005499 | 0.000220 | 24.952404 | 2.010855e-137 | 0.005067 | 0.005931 |
上z可以当作t-statistics看待,从p值可以看出,系数是显著的。
Confounding:
通过简单回归df.students2 model_1和多元回归df[['balance', 'income', 'student2']model_2会发现前者中,学生的系数为正,后者为负。原因是,这个数据里,学生的default率更高(背后原因是因为学生倾向有更高的balance),所以考虑但因素时,model_1中系数为正。然而,当考虑上balance因数后会发现,在相同balance情况下,学生的default率更低(对balance的抵抗力更大),所以学生因素在model_2中成了负因子。现实中,如果不知道一个学生的balance信息,他的违约风险比其他人大。这再次说明单因素回归的危险性。
逻辑回归可用于多分类预测,但不常用。而当classes是well-separated时,逻辑回归的参数估计很不稳定,下面模型能够克服这个问题。
3.3 Linear Discriminant Analysis
当样本量小,且predictors在各个classes中的分布接近normal时,此模型比逻辑回归模型更稳定。
在不同的classes/labels情况下,找出属于该class的observation的分布,然后根据贝叶斯理论,利用这些分布来推测predictors所属的classes,哪个概率最大推测哪个。下面贝叶斯公式中,\(\pi_k\) 是class~k~在整个样本中的比例;\(f_k (x)\) 是x在class~k~中的密度函数/分布,即已知\(Y=k\) ,\(X=x\)的概率是多少;分子不影响结果大小的顺序,可不管。
\[ \mathrm{Pr}(Y = k|X = x) = \frac{π_k f_k (x)}{\sum^K_{l=1} π_lf_l(x)} \]
\(\pi_k\) 比较好计算 \(\hat{π}_k = n_k / n\),问题在于如何得出 \(f_k (x)\)。
3.3.1 LDA计算
LDA假设 \(f_k (x)\) 都是正太分布,且各分布同方差
当p=1,即一个predictor时
密度函数如下
\[ f_k(x) = \frac{1}{\sqrt{2πσ}} exp (-\frac{1}{2σ^2} (x−μ_k)^2) \]
通过样本推断出分布的均值和方差(假设同方差,所以用样本求各自方差后加权平均),然后把x的值代入不同的 \(f_k (x)\) 再乘上相应的 \(\hat{π}_k\) ,最后选取结果最大的class作为预测结果。另一对class的结果相等就能解出两者间的决策边界。
当p>1
密度函数如下
\[ f_k(x) = \frac{1}{(2π)^{p/2}|\Sigma|^{1/2}} exp (-\frac{1}{2}(x-\mu_k)^{\mathrm{T}}\Sigma^{-1}(x−μ_k)) \]
这里 \(x\) 是n纬向量,重点是 \(\mu_k\) 和 \(\Sigma\) 。前者是一个向量(\(\mu_1, \mu_2,...\mu_n\)),后者是n x n的协方差矩阵。计算流程和p=1一样。当n = 2,classes数量为3时,各 \(f_k (x)\) 分布的平面图如下左图。
上左图的一个椭圆的范围包含了该class 95%的概率。由于两个predictors有相关性,如上右图所示,所以分布成了椭圆,即便同方差。虚线划分是贝叶斯决策边界,实线为LDA计算出的决策边界。
X = df[['balance', 'income', 'student2']].as_matrix()
y = df.default2
lda = LinearDiscriminantAnalysis(solver='svd')
y_pred = lda.fit(X, y).predict(X)3.3.2 QDA计算
去除各class同方差的限制,决策边界不在是直线。
LDA和QDA的选择在于bias-variance trade-off。前者只有kp个系数要估计,限制更多,variance更低,但bias更高,适合于样本小和各class分布的方差差别不大的情况;后者有kp(p+1)/2个要估计,其他反之。
如果向LDA添加所有的二次项和交互项,它会和QDA一样。
3.4 比较分类方法
LR和LDA两者都是线性模型(式子转换后很相似),区别在于系数的估计方法,前者用maximum likelihood,后者用来自正态分布的mean和variance。两者的选择在于数据是否来自于同方差的正态分布,数据是否相关不影响。
KNN是非参方法,比较适合非线形的决策边界。
QDA处在上面两类之间
3.5 Lab
df = pd.read_csv('Data/Smarket.csv', index_col=0)
# 了解下面两个变量和其他所有变量的相关系数
df.corr()[["Volume","Today"]]
# factoriesDirection,可以用factorize()[0],但具体编码取决于数据的顺序
df['Direction2'] = df.Direction.map(lambda x: 1 if (x == "Up") else 0)
#LR
# sklearn
feature = ["Lag1", "Lag2", "Lag3", "Lag4", "Lag5", "Volume"]
x = df[feature].values
y = df["Direction2"].values
log_reg = LogisticRegression()
log_reg.fit(x,y)
# statsmodels方便分析
y = df['Direction2']
x = sm.add_constant(df[feature])
est = smf.Logit(y, x).fit()
est.summary2().tables[1]
est.pred_table(threshold=0.5) # col: pre, row: label
#LDA
train_x = df[df.Year < 2005][['Lag1','Lag2']]
train_y = df[df.Year < 2005]['Direction']
test_x = df[df.Year == 2005][['Lag1','Lag2']]
test_y = df[df.Year == 2005]['Direction']
lda = LinearDiscriminantAnalysis()
pred = lda.fit(train_x, train_y).predict(test_x)
# 查看先验概率
lda.priors_
# 比起confusion_matrix,这个更好用
print(classification_report(y_test, pred, digits=3))
""""
precision recall f1-score support
Down 0.500 0.315 0.387 111
Up 0.582 0.752 0.656 141
avg / total 0.546 0.560 0.538 252
""""
# 调整判断概率
pred_p = lda.predict_proba(test_x4)
np.unique(pred_p[:,1]>0.7, return_counts=True)C4 Resampling Methods
model assessment:评估模型表现的过程
model selection :选择一个模型合适的flexibility的过程
4.1 Cross-Validation
validation set:training和test set对半分。问题:highly variable,training set不足而高估错误率
Leave-one-out cross-validation (LOOCV) 能准确确定针对训练数据的最优flexibility和错误率。问题:如果下面公式不成立(通常是非线性模型),则很耗时,高variance。
\[ CV_{(n)} = \frac{1}{n}\sum_{i=1}^{n}(\frac{y_i-\hat{y}_i}{1-h_i})^2 \]
上面公式中h~i~为leverage statistic(在之前high leverage points有应用),它所在的分母的值介于1/n和1,反映了某观测值的leverage对他所fit的模型的影响,即这个分母是用于抵消观测值的leverage的。
k-Fold Cross-Validation(LOOCV的特例)相对省时,可大致确定最优flexibility,适中的variance。问题:不能较为准确地评估错误率。
4.2 The Bootstrap
用于测量某个对象的标准差,比如系数,且使用范围广。方法是从原始数据集中,通过重复抽样产生多组与原始数据集相同大小的数据集,然后估计这些数据集的某个指标,比如均值\(\hat{\mu}_i\),最后利用\(\hat{\mu}_i\)和他们的均值来求出SE(\(\hat{\mu}\))。
# validation set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.33, random_state=None)
# LOOCV
loo = LeaveOneOut()
loo.get_n_splits(dataframe)
# k-Fold Cross-Validation
kf_10 = KFold(n_splits=10, shuffle=False, random_state=None)
# 上面两个可放在下面的cv里
cross_val_score(model, X, y, cv=kf_10).mean()
# Bootstrap
X, y = resample(X, y) #可调节n_samples,默认和X大小一样。得到的就是resample后的X和对应的yC5 Linear Model Selection and Regularization
用其他拟合方式替代plain 最小二乘法能够提高模型的prediction accuracy和model interpretability
Prediction Accuracy:如果response和predictors的关系是线性的,则最小二乘法估计是无偏的。再者,如果n远大于p,则该估计还是低variance的。但如果n不是远大于p,则会产生一定的variance。在这个阶段,通过限制模型来提高部分bias降低variance。
Model Interpretability :最小二乘法无法自动排除无关变量,一些辅助方法有:Subset Selection, Shrinkage/regularization,Dimension Reduction
5.1 Subset Selection
选择方式:best subset 和 stepwise
前者通过对predictors所有的组合进行回归后选出最优,2^p^种可能。问题:耗时和过度拟合。
后者分(介绍见2.2.2 一些重要问题的变量选择):forward, backward, and mix
选择标准:
RSS和R^2^都倾向与包含所有predictors的模型来得到最低的training error。这并不适合test error的评估,由此本书引出下面两类方法:
(1)用training errord的修正指标:
C~p~ 用于由最小二乘法得出的模型,该值等于 $ \frac{1}{n}(\mathrm{RSS} + 2d\hat{σ}^2)$ 。此式子中,d表示当前模型predictors的数量, \(\hat{\sigma}\) 由包含所有predictors的模型估计,\(2d\hat{σ}^2\) 用于抵消predictor数量的增加所带来的error的减少,如果 \(\hat{\sigma}\) 是无偏估计,那么 \(C_p\) 也是test MSE的无偏估计。
AIC用于由极大似然得出的模型,该值等于 $ \frac{1}{n\hat{σ}^2}(\mathrm{RSS} + 2d\hat{σ}^2)$ 。此式子忽略一个定值。如果随机项是正态分布的,那么极大似然和最小二乘法得出的结果是一样的。可以看出AIC和前面的C~p~是成比例的。
BIC是从贝叶斯的观点出发,公式与上面的类似,只是把\(2d\hat{σ}^2\)改为\(log(n)d\hat{σ}^2\),但对添加predictors的惩罚更大,所以倾向于选择predictors更少的模型。
Adjusted R^2^ 式子:$1-\frac{\mathrm{RSS}/(n − d − 1)}{\mathrm{TSS}/(n-1)} $ 。理论上而言,修正R^2^最高的模型只包含有用的变量。
(2)用validation:
one-standard-error rule:计算每个模型的test MSE,然后从test error在一个标准差内的模型中选test MSE最低的。
5.2 Shrinkage Methods
除了选predictors的子集来回归,也可以通过regularizes来筛选变量。使用前要standardizing
Ridge Regression
通过调整ridge regression coefficient estimate $\hat{β}_λ^R $,即RSS里的系数,来最小化 \(\mathrm{RSS} + λ \sum_{j=1}^{p}\beta_j^2\) 。二项称为shrinkage penalty,或写作λ||β||~2~ 。式子中 \(\lambda ≥ 0\) ,用于调节惩罚的权重。当\(\lambda = 0\)时,\(||\hat{β}_λ^R||_2 = ||\hat{\beta}||_2\)。随着\(\lambda\)的增大,各个predictors的系数$\hat{β}_λ^R $会进行调整(总体减少)。
Ridge Regression 优于最小二乘法在于它的bias-variance trade-off,意味着它可以在test set中表现得更好。
Lasso Regression 能够去除一些不显著的变量(另它的系数为0)。shrinkage penalty改为 \(λ \sum_{j=1}^{p}|\beta_j|\) 或λ||β||~1~
两者适合的场景取决于有多少个无用的predictors,由于各个predictors的作用是未知的,所以一般用cross-validation来确定选择。
补充:
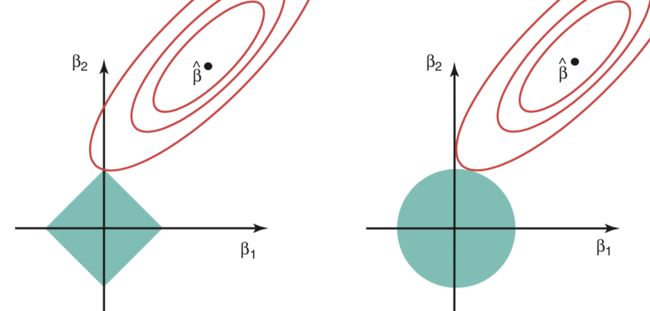
上面两个回归等价于: minimize RSS subject to \(\sum_{j=1}^{p}\beta_j^2 ≤ s\) or \(\sum_{j=1}^{p}|\beta_j| ≤ s\) ,其中s对应于\(-\lambda\) ,即lambda越小,s越大,回归的限制越小。从这个角度来看,两个回归在数学上相当于best subset selection的改良版,因为后者受限于\(\sum_{j=1}^{p}I(\beta_j \ne 0) ≤ s\) 。另外,通过这个角度,这两个回归就能在图像中体现:
上图部分说明了为什么Lasso能够产生sparse解,因为交点会出现在坐标走上,而Ridge不会。
5.3 Dimension Reduction Methods
记得standardizing(以相同单位测量的除外)
对predictors进行降维(将p个变为m个),转化后的predictors为 $Z_m = \sum_{j=1}^p \phi_{jm}X_j $ (每一个Z都是所有predictors的线性组合)其中m = 1,...,M,M
\[ y_i = \theta_0 + \sum_{m=1}^{M} \theta_mz_{im} + \epsilon_i, \ \ \ \ \ i = 1,...,n \]
5.3.1 PCA
以一个包含两个变量pop和ad的数据为例,转换后得到的第一个Z~1~称为第一主成分,其等式如下:
\[ Z_1 = 0.839 × (pop − \bar{pop}) + 0.544 × (ad − \bar{ad}) \]
其中loadings φ~11~ = 0.839 和 φ~21~ = 0.544,它们是在 \(\phi_{11}^2 + \phi_{21}^2 = 1\)的条件下,使 $\mathrm{Var}(\phi_{11} × (pop − \bar{pop}) + \phi_{21} × (ad − \bar{ad})) $ 最大化得出的,为了尽量保存数据的variance。loadings越大,说明该predictors在此主成分占有的信息越大。而Z~2~是在与Z~1~正交,即不相关,的情况下得到的,其他Z如此类推。如果pop和ad的相关性很大,那么Z~1~(下图绿线)能够很好的保存这两个变量的信息,而Z~2~(下图虚线)由于与Z~1~正交,所以不能很好地使得所有的pop和ad都落在附近,所以保留的信息就少。在回归时只回归Z~1~就可以了。
其实ridge相当于连续性的PCR。用于回归时,M的选择可以根据cross-validation;用于数据分析时,M可以根据以PVE和M为坐标的图中找拐点选择,或者开始看第一主成分,如果有感兴趣的特征,再加上第二主成分。
使用:PCA通常只在有很多predictors的情况下才表现的更好,机器正常能处理的数据一般不需要用。另外,由于降维所得到的主成分是unsupervised,所以无法保证它们是最适合回归的。
5.3.2 PLS
PLS在降维得出Z~1~的时候,把更多的权重赋给与response更相关的变量。而Z~2~则从“对Z~1~的每一个变量进行回归后提取得到的residuals”中采用Z~1~同样的方法获得。然而此方法的实际表现并不比PCA好。
5.4 思考高维数据
在数据不足的情况下:最小二乘法没有最优解,即便有,也会过度拟合,所以MSE和R~2~失效。但其他修正指标在高维数据中估计所需的\(\hat{\sigma}\)也有问题。这些问题同样会出现在传统的线形模型中。这时需要的是独立测试或者cross-validation。而在回归方面就需要本章提到的一些方法,如ridge、lasso、stepwise selection、PCA等来防治过度拟合。在高维数据中,正确地判断\(\lambda\)能够在提高模型的表现,但除非附加特征与response正相关,否则测试误差始终会随着问题predictors的增加而增加。
在高维数据中,多重共线性会很严重的,这使得我们无法判断哪个变量才是真正有用的。即便使用stepwise所得到的模型,也只是众多可行模型中的一个,或许还只在某个特定数据集可行。
5.5 Lab
# 下面三行作阅读理解,用sklearn的onehot更方便
dummies = pd.get_dummies(df[['League', 'Division', 'NewLeague']])
X_ = df.drop(['Salary', 'League', 'Division', 'NewLeague'], axis=1).astype('float64')
X = pd.concat([X_, dummies[['League_N', 'Division_W', 'NewLeague_N']]], axis=1)
# Ridge(和lasso类似)如果结果想和书本的几乎一样,需要安装一个新模块python-glmnet
ridge = Ridge(alpha) # alpha是惩罚系数
ridge.fit(scaler.transform(X_train), y_train) # scale相当于简单化的StandardScaler,没有fit和transform
pred = ridge.predict(scaler.transform(X_test))
mean_squared_error(y_test, pred)
pd.Series(ridge2.coef_.flatten(), index=X.columns)
# cross-validation训练ridge
ridgecv = RidgeCV(alphas, scoring='neg_mean_squared_error') #alphas是一个lambda值数组
ridgecv.fit(scale(X_train), y_train)
ridgecv.alpha_ # 得出最优alpha
# PCA
pca = PCA()
X_reduced = pca.fit_transform(scale(X)) # 得到主成分,默认多少predictors就多少个
pca.components_ # 查看loadingsC6 非线性模型
本章介绍的方法能尽量保留interpretability,算是向非线形模型方向前进的一小步。
6.1模型介绍
1~4可以看作是简单线性的扩展。5则是多元回归
6.1.1 Basis Functions
多项回归
\[ y_i =β_0 +β_1x_i +β_2x^2_i +β_3x^3_i +...+β_dx^d_i +\epsilon_i \]
一般来说,d很少大于4,因为会过度flexible,产生奇怪的形状,尤其是在predictors的边界。左下图表示多项回归的结果。虚线代表95%的置信区间。从图中可以看出,wage可以分以250为边界分为两组,由此运用多项逻辑回归。结果如有下图,由于wage>250在总体里站很小的比重,所以95%的置信区间会很宽。
Step functions:把numerical变量变为categorical后回归。
Basis Functions :就是将上面两种functions的式子写到一起。
\[ y_i = β_0 + β_1b_1(x_i) + β_2b_2(x_i) + β_3b_3(x_i) + ... + β_Kb_K(x_i) + \epsilon_i. \]
上面的 $b_K(·) $ 既可以是 $b_j(x_i) = x^j_i $ (多项)也可以是 $b_j(x_i) = I(c_j ≤ x_i < c_{j+1}) $ (step)
6.1.2 Regression Splines
Piecewise Polynomials:将变量进行分区,在不同区域运用相同形式的多项回归,自由度为所有多项回归系数的数量。由于过于flexible,各分区之间会出现断点。
Continuous Piecewise:通过添加限制是函数变成连续。下面以cubic spline with K个断点结合Basis Functions的模型为例:
\[ y_i = β_0 + β_1b_1(x_i) + β_2b_2(x_i) + · · · + β_{K+3}b_{K+3}(x_i) + \epsilon_i \]
有n个分区就加上n-1个系数,其中 \(b(x_i) = h(x_i, ξ)\) 。当 \(x_i > ξ\) 等于 \((x-ξ)^3\) ,否则等于0。这样回归的结果就能在二次求导内保持连续的效果。
添加additional boundary constraints 成为natural cubic spline,即在x的两个边界部分限制为线性来减少这两部分的variance。
断点的选择:在数据变化剧烈的区域多设断点,虽然实践中通常按数据比例进行划分,如25%,50%和75%,或者cross-validation。
与多项回归的比较:当spline的自由度和多项式的degree水平一样时,前者通常更好。
6.1.3 Smoothing Splines
最小化目标函数:
\[ \sum_{i=1}^{n}(y_i − g(x_i))^2 + λ\int g′′(t)^2dt \]
第二项是惩罚项,积分的是整个函数在一阶导数的总变化。如果g很平滑(直线),那么惩罚项就小,反之。(二阶导数就是测量函数变化的剧烈程度的,如果值为0,说明函数在该点平滑/直线)当惩罚系数无穷大时,g就会变成直线,反之g会interpolate。
其实这个函数类似shrunken 版本的piecewise natural cubic polynomial,惩罚系数控制shrinkage 程度,另外所有 unique values of x1,...,xn 都是断点。
惩罚系数的选择:用LOOCV
λ increases from 0 to ∞, effective degrees of freedom($df_λ $) decrease from n to 2
6.1.4 Local Regression
计算某个x的target只用该点附近的x来推定,这个附近用比例s确定,可设置一些变量为global,有些为local。然而当变量多于3个时,变现并不好,因为附近没有那么多observation用于训练。类似KNN的问题。
6.1.5 Generalized Additive Models
additive model: 一个自然的方法是把所有 \(β_jx_{ij}\) 换成 $f_j(x_{ij}) $ ,得到 $y_i = β_0 +f_1(x_{i1})+f_2(x_{i2})+···+f_p(x_{ip})+ \epsilon_i $ 然后每个 \(f_i\) 可以是上面1~4所介绍的函数。
由于additive,对于每个变量对response的影响还是可以解释的。这个模型为参数和非参数方法提供了一个折中。
在分类0/1问题中,如果某个 $f_j(x_{ij}) $ 中x是categorical,且里面的某个类别连一个1都没有,则要去掉。
C7 Tree-Based Methods
尽管decision tree比不上C5和C6的方法,但bagging和random forests在prediction方面可以有很大提升。
7.1 决策树基础
回归树最小化RSS,目标函数:
\[ \sum_{j=i}^J \sum_{i\in R_j}(y_i - \hat{y}_{R_j})^2 \]
其中J代表terminal node的集合,R~j~表示第j个node,\(\hat{y}_{R_j}\) 表示该node的预测值。
通常会设置一个 \(\alpha\) 来作惩罚系数,防止过度拟合。
分类树最小化分类错误率,Gini或entropy:
\[ E = 1 − max_k( \hat{p}_{mk}) \ \ \ , \ \ \ \mathrm{Gini}: G = \sum_{k=1}^K \hat{p}_{mk}(1- \hat{p}_{mk}) \ \ \ , \ \ \ \mathrm{entropy}: D = - \sum_{k=1}^K \hat{p}_{mk}log\ \hat{p}_{mk} \]
其中 \(\hat{p}_{mk}\) 表示第m个terminal node中kth class的比例。由于分类错误率对树的成长不敏感,所以通常用后面两种,但对于树的判读正确率,E表现更加理想。
树的优缺点:易于解释和运用,但对样本数据的变化很敏感,且效果不比之前介绍的方法好。
7.2 Bagging, Random Forests, Boosting
树够多的话,前两个不会overfitting
Bagging
bootstrap多组数据集来建树,对于回归,取树的均值;对于分类,最多投票的class。
Out-of-Bag (OOB) Error Estimation
变量重要性测量:某变量的划分对RSS/Gini or entropy减少的总量
Random Forests
划分时考虑随机选取的部分样本,为了防止生长成相同的树。其他和bagging一样。
Boosting
每棵树在前一个棵树的训练数据的修改版response的residual部分上进行训练。树数量,学习速度,树的深度等需要cross-validation决定
C8 SVM
8.1 Maximal Margin Classifier
Hyperplane:在p维空间里,a flat affine(不过原点) subspace of dimension p − 1。下面式子定义一个超平面:
\[ β_0 +β_1X_1 +β_2X_2 +...+β_pX_p = 0 \]
任何 $X = (X_1,X_2,...,X_p)^T $ 表示超平面上的一个点。如果式子变为大于小于,那么表示该点处于超平面的其中一边。
support vectors:影响边界的observation,此方法中是在margin边界上的observation
最大化边界M,数学表达如下:
\[ \mathop{maximise} \limits_{β_0 ,β_1 ,...,β_p,M} M \\ \mathrm{subject\ to}\ \ \ \sum_{j=1}^p \beta^2_j=1\ \ \ \mathrm{and}\ \ \ y_i(β_0 +β_1x_{i1} +β_2x_{i2} +...+β_px_{ip})≥M \ \ ∀i=1,...,n \]
限制是为了每个observation都在正确的一边,而且距离至少为M。
由于此方法在分界上过度敏感,且有时数据不是完全可分的,所以引出下面方法。
8.2 Support Vector Classifiers(soft margin classifier)
允许observation落在错误的一侧(超过margin)
\[ \mathop{maximise} \limits_{β_0 ,β_1 ,...,β_p,\epsilon_1,...,\epsilon_n} M \\ \mathrm{subject\ to}\ \ \ \sum_{j=1}^p \beta^2_j=1 \ \ \ \ ,\ \ \ y_i(β_0 +β_1x_{i1} +β_2x_{i2} +...+β_px_{ip})≥M(1-\epsilon_i)\ \ \ \mathrm{and}\ \ \ \epsilon_i ≥ 0,\ \ \ \sum_{i=1}^n \epsilon_i \leq C \]
上面 \(\epsilon_i\) 是slack variables,等于0是正确划分,大于0小于1是在margin里错误的一边,大于1就是在margin外错误的一边。C代表对这些错误的总量。
此方法中的support vectors是边界上以及错误地超越边界的observation。
然而此方法的分界依然是线性的,为了解决不同class数据非线性分堆的问题,需要下面方法。
8.3 Support Vector Machines
通过enlarging the feature space,即用平方、立方或更高阶的多项式实现。利用kernel trick可以简化这些多项式:
两观测值的内积: \(⟨x_i,x_{i^{'}}⟩ = \sum_{j=1}^p x_{ij}x_{i^{'}j}\)
linear support vector classifier 可以简化为:\(f(x) = \beta_0 + \sum_{i=1}^n a_i⟨x,x_i⟩\) 其中 \(\alpha\) 是每个observation都要估计的系数,但如果该观测值不是support vector,则该系数为0。
为了估计这个函数,需要计算内积,把上面的内积归纳为: \(K(x_i,x_{i^{'}})\) ,K成为kernel,一个量化两个observation相似程度的函数。上面的kernel是线性的,也可以改用其他形式的kernel。当support vector classifier 采用其他非线形kernel时,称为SVM。
radial kernel(rbf)根据附近的observation划分,需要调节gamma,越大越flexible
多个分类以上的SVM:One-Versus-One 和 One-Versus-All
SVM和LR类似,因为8.2中的式子可以改写如下:
\[ \mathop{maximise} \limits_{β_0 ,β_1 ,...,β_p} ^{}\left\{\sum_{i=1}^{n} \mathrm{max}[0, 1 - y_if (x_i)] + \lambda \sum_{j=1}^{p}\beta^2_j \right\} \]
第一部分loss function(hinge loss)和LR的很类似,只是对于非support vector,SVM的loss为0,LR中远离分界线的接近0。总的来说,SVM在 well-separated classes时表现更好,重叠多时后者更好。
8.4 Lab
svc2 = SVC(C=0.1, kernel='linear')
# 用cross-validation
tuned_parameters = [{'C': [0.001, 0.01, 0.1, 1, 5, 10, 100]}]
clf = GridSearchCV(SVC(kernel='linear'), tuned_parameters, cv=10, scoring='accuracy', return_train_score=True)
clf.fit(X, y)
clf.cv_results_
clf.best_params_C9 Unsupervised Learning
PCA
9.1 Clustering Methods
K-Means
目标:同类的variation尽量小
\[ \mathop{maximise} \limits_{C_1 ,...,C_k} ^{}\left\{\sum_{k=1}^{K} W(C_k) \right\} \]
C~k~表示第k个cluster,W(.)表示衡量variation的函数,具体实现有很多,例如L2。
K-Means的一个问题是需要预先设置K的个数,而hierarchical clustering可以后来再设K。
hierarchical clustering
相似度根据两个observations交汇点的高度,越高越不相似。下左图,2,8,5和7与9的交汇高度是一样的。
分类就看从哪个高度水平切开,得出多少树枝就多少类。
这个方法的问题出现在这么一个场景:在一组数据中,如果分成两组的最优解是男/女,而分成三组的最优解是国籍(三个国家)。这个方法分三组的最优方法会是在男/女的基础上把男或女的组尽心拆分。在这种情况下,它分类的“准确性”比KMeans差。
实现的过程:一开始n个clusters,然后组合最接近的两个observation得到n-1个cluster,然后不断重复。判断两个cluster接近程度的方法有:complete,average,single和centroid,前两者最受欢迎,因结果树更加平衡。
补充:
Dissimilarity Measure 的选择:距离或者关系。例如按距离来分,会把购买量类似的顾客分为一类;按关系来分,会把购买种类类似的顾客分为一类。
对于数据的scale取决于应用的场景。
上面两个方法的问题:会对一些outliers强行分类。
参考:
Introduction to Statistical Learning