机器人动力学（Basic Newton-Euler Mechanics）

前言

为什么要考虑运动学？因为运动学的速度是一个理想化的一个量，让它为0，立马就能为0，然鹅现实中它不可能瞬间就变成0，他还需要制动。另外就是加速度的限制：使得车能在车轮不打滑或者车不会翻过来的情况下在一定时间内达到最大速度。
动力学 隐式表达：
$$g_i(\ddot{q},\dot{q},q)=0$$
动力学 显示表达：
$$\ddot{q}=f(\dot{q},q,u)$$
由于高阶导数计算比较困难，这里引入相空间来对其进行简化，类似于非线性规划中的相平面。

重要坐标系

1. Inertial frame：固定的全局坐标系
2. Translating frame：固定在运动体上的坐标系，原点在质心，但轴平行于Inertial frame
3. Body frame：固定在运动体上的坐标系，质点在质心，轴随着质点运动会改变方向

刚体运动

预备知识

角动量:L=r X p(p为O点的动量，r是质点相对O点的位矢)
力矩：N=F X r（F为O点的力，r是质点相对O点的位矢），还等于dL/dt(L为角动量，角动量定理)

$A\subseteq {\mathbb{R}}^3$代表一个刚体. $\sigma (r)$ 代表在 $r\in A$的一点的刚体密度，$m$ $A$的总质量:
$$m={\int }_A\sigma (r)dr$$

$dr=d{r}_{1}d{r}_{2}d{r}_3$ 代表一个柱状的体积，$p\in {\mathbb{R}}^3$ 表示 $A$的质心, $p=(p_1,p_2,p_3)$：

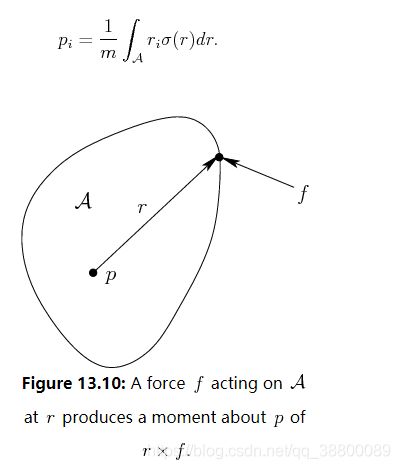
由于刚体的内部力相互抵消，外部边界的力的集合可以合成一个力F和力矩N作用在质点p：

移动

刚体不旋转值只移动：动量

由牛二定理：

可以得到六个状态转移方程：

旋转

旋转可以同移动进行解耦，所以现在只在 translating frame中考虑纯粹的旋转运动。E为角动量，则力矩为：
参考角动量定理


参考上面图13.11，旋转角速度：v是单位向量，表示旋转方向，$\theta$表示旋转角度

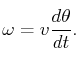
将此角速度转化成，yaw-pitch-roll形式表示的旋转角速度：

惯性矩（通常平面刚片且是均质的，则也称为转动惯量）

E是整个刚体的角动量

经过以下一系列操作，主要是点乘和叉乘之间的转换：

惯性矩阵3 X 3对称矩阵：

则刚体的角动量：

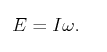
刚体所受到的力矩：

注意上面求得的惯性矩阵是在translating frame中考虑的，它会随着旋转q的变化而变化：

这里我们将惯性矩阵定义在body frame中，表示成I，则I与I（q）的关系（其中R是body frame到 translational frame的旋转矩阵。）：

则刚体所受到的力矩简化为：

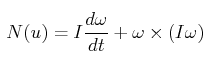
如果选择的body frame等于惯性主轴，那么惯性矩阵就简化为：

列写动力学方程

这里假设选择的body frame等于惯性主轴，求得角加速度方程：

结合移动那一节的三个方程，以及角速度和四元数（表示旋转角度）的关系，我们就得到了12个动力学方程：