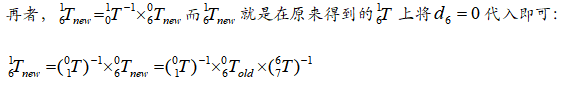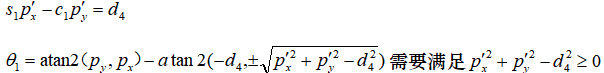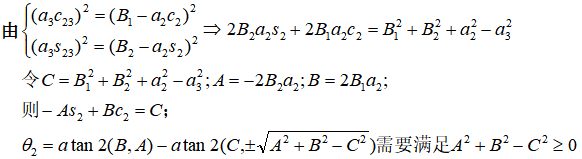（6）六轴机械臂的运动学正、逆解
下面在前面的ur5机械臂的DH参数基础是对其正逆解进行求解，为了后面能在MATLAB中利用stl文件进行实际显示，这里以标准DH参数为例进行讲解。（修正DH参数在用plot3d函数是显示失败，不知道是不是这个函数只能显示标准dh参数的机械臂模型，有知道的网友可以在评论里告知一下，谢谢。）
一、运动学正解：
机器人正运动学是在已知各连杆相对位置关系（关节角）的情况下，得到末端执行器的位姿。在标准DH参数下相邻坐标系之间的齐次变换矩阵为：
则，正解代码如下：
function [T06,Pos]=ForwardSolver_MDH(theta)
DH_JXB =[90 0 144 0;
0 264 0 90;
0 236 0 0;
-90 0 106 -90;
90 0 114 0;
0 0 67 0];
d=DH_JXB(1:6,3);
a=DH_JXB(1:6,2);
DH_JXB(1:6,1)=DH_JXB(1:6,1)/180*pi; %度数转化为弧度
alp=DH_JXB(1:6,1);
offset=[0 90 0 -90 0 0];
theta=(theta+offset)*pi/180;
for i=1:6
T{i}=[ cos(theta(i)), -sin(theta(i))*cos(alp(i)), sin(theta(i))*sin(alp(i)), a(i)*cos(theta(i));
sin(theta(i)), cos(theta(i))*cos(alp(i)),
-cos(theta(i))*sin(alp(i)), a(i)*sin(theta(i));
0, sin(alp(i)), cos(alp(i)), d(i);
0, 0, 0, 1
]
end
disp('Homogeneous transformation matrix T06:')
T06=T{1}*T{2}*T{3}*T{4}*T{5}*T{6}
%% 求末端位置
X=T06(1,4);Y=T06(2,4);Z=T06(3,4);
%% 求末端姿态Rotations about X, Y, Z axes (for a robot gripper)
R=T06;
if abs(abs(R(1,3)) - 1) < eps % when |R13| == 1
% singularity
rpy(1) = 0; % roll is zero
if R(1,3) > 0
rpy(3) = atan2( R(3,2), R(2,2)); % R+Y
else
rpy(3) = -atan2( R(2,1), R(3,1)); % R-Y
end
rpy(2) = asin(R(1,3));
else
rpy(1) = -atan2(R(1,2), R(1,1));
rpy(3) = -atan2(R(2,3), R(3,3));
rpy(2) = atan(R(1,3)*cos(rpy(1))/R(1,1));
end
RPY=rpy*180/pi;
Rall=RPY(1);Pitch=RPY(2);Yaw=RPY(3);
Pos=[X,Y,Z,Rall,Pitch,Yaw];
end这里对姿态的描述进行说明：在MATLAB中RPY欧拉角是世界坐标系下的XYZ欧拉角；
RPY角的定义如下：
输入端位姿形式为：
MATLAB中对应的RPY旋转矩阵如下：
这是个旋转矩阵，与齐次矩阵中的旋转矩阵等价，所以根据齐次矩阵中的旋转矩阵便可以得到末端的姿态RPY。
二、运动学逆解：
机器人逆运动学是已知机器人末端执行器的位姿，通过变换矩阵T得到机器人各关节的角度。求解逆运动学有解析法、几何法、迭代法。这里介绍解析法。如果机器人末端三轴的轴线始终交于一点则该机器人必有解析解。
1、得到齐次变换矩阵：
利用MATLAB求解其齐次变换矩阵：
syms a1 a2 a3 a4 a5 a6 d1 d2 d3 d4 d5 d6 a1p1 a1p2 a1p3 a1p4 a1p5 a1p6 th1 th2 th3 th4 th5 th6;
a=[0 a2 a3 0 0 0];
d=[d1 0 0 d4 d5 d6];
alp=[90 0 0 -90 90 0]*pi/180;
theta=[th1 th2 th3 th4 th5 th6];
% theta(1)=t1;theta(2)=t2;theta(3)=t3;theta(4)=t4;theta(5)=t5;theta(6)=t6;
T01=[ cos(theta(1)), 0, sin(theta(1)), a(1)*cos(theta(1));
sin(theta(1)), 0, -cos(theta(1)), a(1)*sin(theta(1));
0, 1, 0, d(1);
0, 0, 0, 1
];
T12=[ cos(theta(2)), -sin(theta(2)), 0, a(2)*cos(theta(2));
sin(theta(2)), cos(theta(2)), 0, a(2)*sin(theta(2));
0, 0, 1, d(2);
0, 0, 0, 1
];
T23=[ cos(theta(3)), -sin(theta(3)), 0, a(3)*cos(theta(3));
sin(theta(3)), cos(theta(3)), 0, a(3)*sin(theta(3));
0, 0, 1, d(3);
0, 0, 0, 1
];
T34=[ cos(theta(4)), 0, -sin(theta(4)), a(4)*cos(theta(4));
sin(theta(4)), 0, cos(theta(4)), a(4)*sin(theta(4));
0, -1, 0, d(4);
0, 0, 0, 1
];
T45=[ cos(theta(5)), 0, sin(theta(5)), a(5)*cos(theta(5));
sin(theta(5)), 0, -cos(theta(5)), a(5)*sin(theta(5));
0, 1, 0, d(5);
0, 0, 0, 1
];
T56=[ cos(theta(6)), -sin(theta(6)), 0, a(6)*cos(theta(6));
sin(theta(6)), cos(theta(6)), 0 a(6)*sin(theta(6));
0, 0, 1, d(6);
0, 0, 0, 1
];
T06=simplify(T01*T12*T23*T34*T45*T56)
利用三角函数的两角和差公式进行化简：
可以得到：
逆解输入的参数是末端的位姿
，其中
是绕z轴的旋转角度，
是绕y轴的旋转角度，
是绕x轴的旋转角度。这里还需要注意一个问题，MATLAB的.teach()函数输出的图形角度如下图所示：R表示的是世界坐标系到末端坐标系需要绕z轴转动的角度；P表示的是世界坐标系到末端坐标系需要绕y轴转动的角度；Y表示的是世界坐标系到末端坐标系需要绕x轴转动的角度；
则R对应，P对应，Y对应；表示的是末端坐标系绕自身的xyz轴旋转对应的角度后会与基坐标系平行。这里利用XYZ欧拉角公式，
其对应的旋转矩阵为：
根据输入的Pos参数也能得到一个齐次矩阵：
简记为：
而T06乘以
得到下式：
由于不存在常数项（不包含角度θ的项）；所以需要进一步化简，由上式知如果d6=0则存在常数项。
所以，我们做如下处理，类比于增加一个新连杆，且该连杆不转动而是与连杆6固连，如下表所示：
然后让d6=0，而d7=d6，新连杆的坐标系与连杆6完全重合，（这里需要注意变化前后总的齐次变换矩阵是不变的即原来的T06与现在的T07是一模一样的即
）其齐次矩阵为：
又，
故：
然后便可以求出相应角度的表达式：
这里首先介绍个万能公式：
①求解关节1、5、6角度：
由上面的R34相等得：
由R31、R32、R33相等得：
②、求关节2、3、4的角度：
由R13、R23相等得：
由R14、R24相等得：
以上便是所有关节角度的求解公式。
MATLAB代码如下（有点长删掉了部分）：
function AllSloverTheta =InverseSolver_MDH(Pos)
coder.extrinsic('disp');
AllSloverTheta = zeros(8,6);A=zeros(1,4);
DH_JXB =[90 0 144 0;
0 264 0 90;
0 236 0 0;
-90 0 106 -90;
90 0 114 0;
0 0 67 0];
p2=DH_JXB(2,4); %第二轴偏移角度
p4=DH_JXB(4,4); %第四轴偏移角度
%杆长数据
a2=DH_JXB(2,2);
a3=DH_JXB(3,2);
d1=DH_JXB(1,3);
d4=DH_JXB(4,3);
d5=DH_JXB(5,3);
%d6=DH_JXB(6,3);
%输入的位姿数据
X=Pos(1);
Y=Pos(2);
Z=Pos(3);
gama=Pos(4)*pi/180; %绕z轴旋转
beta=Pos(5)*pi/180; %绕y轴旋转
alpha=Pos(6)*pi/180; %绕x轴旋转
%逆解中增加的第七杆DH参数
theta7=0; %角度为0
a6=0;
afa6=0;
d7=DH_JXB(6,3); %杆长为第六杆的长度
%得到第七轴的齐次变换矩阵
T67=[cos(theta7), -sin(theta7), 0, a6;
sin(theta7)*cos(afa6), cos(theta7)*cos(afa6), -sin(afa6), -sin(afa6)*d7;
sin(theta7)*sin(afa6), cos(theta7)*sin(afa6), cos(afa6), cos(afa6)*d7;
0, 0, 0, 1];
%由末端位姿（x,y,z,gama,beta,alpha）得到与GUI界面对应的是（x,y,z,R,P,Y）
T_goat=[cos(beta)*cos(gama), -cos(beta)*sin(gama), sin(beta), X;
sin(alpha)*sin(beta)*cos(gama)+cos(alpha)*sin(gama), -sin(alpha)*sin(beta)*sin(gama)+cos(alpha)*cos(gama), -sin(alpha)*cos(beta),Y;
-cos(alpha)*sin(beta)*cos(gama)+sin(alpha)*sin(gama), cos(alpha)*sin(beta)*sin(gama)+sin(alpha)*cos(gama), cos(alpha)*cos(beta), Z;
0, 0, 0, 1];
%得到新的变换矩阵
T06=T_goat/T67;
nx=T06(1,1);
ny=T06(2,1);
ox=T06(1,2);
oy=T06(2,2);
ax=T06(1,3);
ay=T06(2,3);
az=T06(3,3);
px=T06(1,4);
py=T06(2,4);
pz=T06(3,4);
k=0;
ForJudgment=px^2+py^2-d4^2;
if ForJudgment<-1e-6
disp('Out of workspace Unable to solve');
else
if ForJudgment>=-1e-6&&ForJudgment<0
ForJudgment=0;
end
%求解θ1
theta1_1=atan2(py,px)-atan2(-d4,sqrt(ForJudgment));
theta1_2=atan2(py,px)-atan2(-d4,-sqrt(ForJudgment));
%求解θ5
S5_1=sqrt((sin(theta1_1)*nx-cos(theta1_1)*ny)^2+(sin(theta1_1)*ox-cos(theta1_1)*oy)^2);
theta5_1=atan2(S5_1,sin(theta1_1)*ax-cos(theta1_1)*ay);
S5_2=-sqrt((sin(theta1_1)*nx-cos(theta1_1)*ny)^2+(sin(theta1_1)*ox-cos(theta1_1)*oy)^2);
theta5_2=atan2(S5_2,sin(theta1_1)*ax-cos(theta1_1)*ay);
S5_3=sqrt((sin(theta1_2)*nx-cos(theta1_2)*ny)^2+(sin(theta1_2)*ox-cos(theta1_2)*oy)^2);
theta5_3=atan2(S5_3,sin(theta1_2)*ax-cos(theta1_2)*ay);
S5_4=-sqrt((sin(theta1_2)*nx-cos(theta1_2)*ny)^2+(sin(theta1_2)*ox-cos(theta1_2)*oy)^2);
theta5_4=atan2(S5_4,sin(theta1_2)*ax-cos(theta1_2)*ay);
%下面这些量与θ5对应，都有四个解
S234 = [0; 0; 0; 0];
C234 = [0; 0; 0; 0];
B = [0; 0; 0; 0];
B1 = [0; 0; 0; 0];
B2 = [0; 0; 0; 0];
C = [0; 0; 0; 0];
%8个解
theta2 = [0; 0; 0; 0; 0; 0; 0; 0];
theta23 = [0; 0; 0; 0; 0; 0; 0; 0];
theta234 = [0; 0; 0; 0; 0; 0; 0; 0];
theta3 = [0; 0; 0; 0; 0; 0; 0; 0];
theta4 = [0; 0; 0; 0; 0; 0; 0; 0];
%s5不能为0
if abs(S5_1)>1e-6
theta6_1=atan2((sin(theta1_1)*ox-cos(theta1_1)*oy)/S5_1,(-sin(theta1_1)*nx+cos(theta1_1)*ny)/S5_1);
S234(1)=az/S5_1;
C234(1)=(cos(theta1_1)*ax+sin(theta1_1)*ay)/S5_1;
theta234(1)=atan2(S234(1),C234(1));
B1(1)=cos(theta1_1)*px+sin(theta1_1)*py+d5*S234(1);
B2(1)=pz-d1-d5*C234(1);
A(1)=-2*B2(1)*a2;
B(1)=2*B1(1)*a2;
C(1)=B1(1)^2+B2(1)^2+a2^2-a3^2;
if A(1)^2+B(1)^2-C(1)^2>=0
theta2(1)=atan2(B(1),A(1))-atan2(C(1),sqrt(A(1)^2+B(1)^2-C(1)^2));
theta2(2)=atan2(B(1),A(1))-atan2(C(1),-sqrt(A(1)^2+B(1)^2-C(1)^2));
theta23(1)=atan2((B2(1)-a2*sin(theta2(1)))/a3,(B1(1)-a2*cos(theta2(1)))/a3);
theta23(2)=atan2((B2(1)-a2*sin(theta2(2)))/a3,(B1(1)-a2*cos(theta2(2)))/a3);
theta4(1)=theta234(1)-theta23(1);
theta4(2)=theta234(1)-theta23(2);
theta3(1)=theta23(1)-theta2(1);
theta3(2)=theta23(2)-theta2(2);
AllSloverTheta(k+1,:)=[theta1_1 theta2(1)-p2*pi/180 theta3(1) theta4(1)-p4*pi/180 theta5_1 theta6_1];
AllSloverTheta(k+2,:)=[theta1_1 theta2(2)-p2*pi/180 theta3(2) theta4(2)-p4*pi/180 theta5_1 theta6_1];
k=k+2;
end
end
%s5<0
if abs(S5_2)>1e-6
theta6_2=atan2((sin(theta1_1)*ox-cos(theta1_1)*oy)/S5_2,(-sin(theta1_1)*nx+cos(theta1_1)*ny)/S5_2);
S234(2)=az/S5_2;
C234(2)=(cos(theta1_1)*ax+sin(theta1_1)*ay)/S5_2;
theta234(2)=atan2(S234(2),C234(2));
B1(2)=cos(theta1_1)*px+sin(theta1_1)*py+d5*S234(2);
B2(2)=pz-d1-d5*C234(2);
A(2)=-2*B2(2)*a2;
B(2)=2*B1(2)*a2;
C(2)=B1(2)^2+B2(2)^2+a2^2-a3^2;
if A(2)^2+B(2)^2-C(2)^2>=0
theta2(3)=atan2(B(2),A(2))-atan2(C(2),sqrt(A(2)^2+B(2)^2-C(2)^2));
theta2(4)=atan2(B(2),A(2))-atan2(C(2),-sqrt(A(2)^2+B(2)^2-C(2)^2));
theta23(3)=atan2((B2(2)-a2*sin(theta2(3)))/a3,(B1(2)-a2*cos(theta2(3)))/a3);
theta23(4)=atan2((B2(2)-a2*sin(theta2(4)))/a3,(B1(2)-a2*cos(theta2(4)))/a3);
theta4(3)=theta234(2)-theta23(3);
theta4(4)=theta234(2)-theta23(4);
theta3(3)=theta23(3)-theta2(3);
theta3(4)=theta23(4)-theta2(4);
AllSloverTheta(k+1,:)=[theta1_1 theta2(3)-p2*pi/180 theta3(3) theta4(3)-p4*pi/180 theta5_2 theta6_2];
AllSloverTheta(k+2,:)=[theta1_1 theta2(4)-p2*pi/180 theta3(4) theta4(4)-p4*pi/180 theta5_2 theta6_2];
k=k+2;
end
end
if abs(S5_3)>1e-6
theta6_3=atan2((sin(theta1_2)*ox-cos(theta1_2)*oy)/S5_3,(-sin(theta1_2)*nx+cos(theta1_2)*ny)/S5_3);
S234(3)=az/S5_3;
C234(3)=(cos(theta1_2)*ax+sin(theta1_2)*ay)/S5_3;
theta234(3)=atan2(S234(3),C234(3));
B1(3)=cos(theta1_2)*px+sin(theta1_2)*py+d5*S234(3);
B2(3)=pz-d1-d5*C234(3);
A(3)=-2*B2(3)*a2;
B(3)=2*B1(3)*a2;
C(3)=B1(3)^2+B2(3)^2+a2^2-a3^2;
if A(3)^2+B(3)^2-C(3)^2>=0
theta2(5)=atan2(B(3),A(3))-atan2(C(3),sqrt(A(3)^2+B(3)^2-C(3)^2));
theta2(6)=atan2(B(3),A(3))-atan2(C(3),-sqrt(A(3)^2+B(3)^2-C(3)^2));
theta23(5)=atan2((B2(3)-a2*sin(theta2(5)))/a3,(B1(3)-a2*cos(theta2(5)))/a3);
theta23(6)=atan2((B2(3)-a2*sin(theta2(6)))/a3,(B1(3)-a2*cos(theta2(6)))/a3);
theta4(5)=theta234(3)-theta23(5);
theta4(6)=theta234(3)-theta23(6);
theta3(5)=theta23(5)-theta2(5);
theta3(6)=theta23(6)-theta2(6);
AllSloverTheta(k+1,:)=[theta1_2 theta2(5)-p2*pi/180 theta3(5) theta4(5)-p4*pi/180 theta5_3 theta6_3];
AllSloverTheta(k+2,:)=[theta1_2 theta2(6)-p2*pi/180 theta3(6) theta4(6)-p4*pi/180 theta5_3 theta6_3];
k=k+2;
end
end
if abs(S5_4)>1e-6
theta6_4=atan2((sin(theta1_2)*ox-cos(theta1_2)*oy)/S5_4,(-sin(theta1_2)*nx+cos(theta1_2)*ny)/S5_4);
S234(4)=az/S5_4;
C234(4)=(cos(theta1_2)*ax+sin(theta1_2)*ay)/S5_4;
theta234(4)=atan2(S234(4),C234(4));
B1(4)=cos(theta1_2)*px+sin(theta1_2)*py+d5*S234(4);
B2(4)=pz-d1-d5*C234(4);
A(4)=-2*B2(4)*a2;
B(4)=2*B1(4)*a2;
C(4)=B1(4)^2+B2(4)^2+a2^2-a3^2;
if A(4)^2+B(4)^2-C(4)^2>=0
theta2(7)=atan2(B(4),A(4))-atan2(C(4),sqrt(A(4)^2+B(4)^2-C(4)^2));
theta2(8)=atan2(B(4),A(4))-atan2(C(4),-sqrt(A(4)^2+B(4)^2-C(4)^2));
theta23(7)=atan2((B2(4)-a2*sin(theta2(7)))/a3,(B1(4)-a2*cos(theta2(7)))/a3);
theta23(8)=atan2((B2(4)-a2*sin(theta2(8)))/a3,(B1(4)-a2*cos(theta2(8)))/a3);
theta4(7)=theta234(4)-theta23(7);
theta4(8)=theta234(4)-theta23(8);
theta3(7)=theta23(7)-theta2(7);
theta3(8)=theta23(8)-theta2(8);
AllSloverTheta(k+1,:)=[theta1_2 theta2(7)-p2*pi/180 theta3(7) theta4(7)-p4*pi/180 theta5_4 theta6_4];
AllSloverTheta(k+2,:)=[theta1_2 theta2(8)-p2*pi/180 theta3(8) theta4(8)-p4*pi/180 theta5_4 theta6_4];
k=k+2;
end
end
if k>0
AllSloverTheta=AllSloverTheta*180/pi;%将弧度转化成角度
for i=1:k
for j=1:6
if AllSloverTheta(i,j)<=-180
AllSloverTheta(i,j)=AllSloverTheta(i,j)+360;%将角度限定在-180—+180
elseif AllSloverTheta(i,j)>180
AllSloverTheta(i,j)=AllSloverTheta(i,j)-360;%将角度限定在-180—+180
end
end
end
else
disp('Singular position Unable to solve');
end
end
end