模式识别期末复习题
模式识别期末复习题
一、判断
1、影响层次聚类算法结果的主要因素有:计算模式距离的测度、聚类准则、类间距离门限、预定的类别数目。( √ √ √)
2、欧式距离具有平移不变性和旋转不变性。( √ √ √)
3、马式距离既具有欧式距离的特性,还具有尺度缩放不变性和不受量纲影响。( √ √ √)
4、线性判别函数的正负和数值大小的几何意义是:正(负)表示样本点位于判别界面法向量指向的正(负)半空间中;绝对值正比于样本点到判别界面的距离。( √ √ √)
5、积累势函数法较之于 H — K H—K H—K 算法的优点是:该方法可用于非线性可分情况,也可用于线性可分情况。( √ √ √)
6、位势函数 K ( x , x k ) K(x,x_k) K(x,xk) 与积累位势函数 K ( x ) K(x) K(x) 的关系为 K ( x ) = ∑ x k ∈ X α k K ( x , x k ) K(x) =\sum\limits_{x_k\in X}\alpha_kK(x,x_k) K(x)=xk∈X∑αkK(x,xk) 。( √ √ √)
7、在统计模式分类问题中,聂曼-皮尔逊判决准则主要用于:某一种判决错误较另一种判决错误更为重要情况。( √ √ √)
8、“特征个数越多越有利于分类” 这种说法正确吗?( × × ×)
9、特征选择的主要目的是:从 n n n 个特征中选出最有利于分类的的 d d d 个特征( d < n d
10、影响聚类算法结果的主要因素有:分类准则、特征选取、模式相似性测度。( √ √ √)
11、影响 C C C 均值算法的主要因素有:样本输入顺序、模式相似性测度、初始类心的选取。( √ √ √)
12、位势函数法的积累势函数 K ( x ) K(x) K(x) 的作用相当于 B a y e s Bayes Bayes 判决中的后验概率或类概率密度与先验概率的乘积,而不是先验概率和类概率密度。( √ √ √)
13、在统计模式分类问题中,当先验概率未知时,可以使用②最小最大损失准则和 N − P N-P N−P 判决而不用最小损失准则和最小误判概率准则。( √ √ √)
14、似然函数的概型已知且为单峰,则可用矩估计、最大似然估计、 B a y e s Bayes Bayes 估计、 B a y e s Bayes Bayes 学习和 P a r z e n Parzen Parzen 窗法估计该似然函数。( √ √ √)
15、从分类的角度讲,用 D K L T DKLT DKLT 做特征提取主要利用了 D K L T DKLT DKLT 的性质是:变换产生的新向量正交或不相关、 使变换后的矢量能量更趋集中。( √ √ √)
二、选择题或填空题
详细的参考教材书。
1、聚类分析算法属于( A A A)
A . A. A. 无监督分类 B . B. B. 有监督分类 C . C. C. 统计模式识别方法 D . D. D. 句法模式识别方法
2、 判别域代数界面方程法属于( B B B)。
A . A. A. 无监督分类 B . B. B. 统计模式识别方法 C . C. C. 模糊模式识别方法 D . D. D. 句法模式识别方法
3、若描述模式的特征量为 0 − 1 0-1 0−1 二值特征向量,则一般采用( D D D)进行相似度量。
A . A. A. 距离测度 B . B. B. 模糊测度 C . C. C. 相似测度 D . D. D. 匹配测度
4、 下列哪个函数不作为聚类分析中的准则函数 ( B B B) 。
A . J = t r ( S ω − 1 S b ) A.J=tr({S_\omega}^{-1}S_b) A.J=tr(Sω−1Sb) B . J = ∣ S ω S b − 1 ∣ B.J=|S_\omega{S_b}^{-1}| B.J=∣SωSb−1∣
C . J = ∑ j = 1 c ∑ i = 1 N i ∣ ∣ x i ( j ) − m j ∣ ∣ 2 C.J=\sum\limits_{j=1}^{c}\sum\limits_{i=1}^{N_i}||{x_i}^{(j)}-m_j||^2 C.J=j=1∑ci=1∑Ni∣∣xi(j)−mj∣∣2 D . J = ∑ j = 1 c ( m j − m 0 ) T ( m j − m 0 ) D.J=\sum\limits_{j=1}^{c}(m_j-m_0)^T(m_j-m_0) D.J=j=1∑c(mj−m0)T(mj−m0)
5、下列判别域界面方程法中只适用于线性可分情况的算法有( A D AD AD)。
A . A. A. 感知器算法 B . B. B. H − K H-K H−K 算法 C . C. C. 积累位势函数法 D . D. D. 费歇尔线性判别法
6、线性可分、不可分都适用的有( C C C)。
A . A. A. 感知器算法 B . B. B. H − K H-K H−K 算法 C . C. C. 积累位势函数法 D . D. D. 费歇尔线性判别法
7、遗传算法的基本操作有( A A A)。
A . A. A. 复制(选择)、交叉、变异 B . B. B. 适应、交叉、变异 C . C. C. 群体、个体、变异
8、 A S O ASO ASO 算法中,信息素是( C C C)。
A . A. A. 常数 B . B. B. 随机增大 C . C. C. 有一定挥发 D . D. D. 任意变化
9、 B P BP BP 网络是( C C C)网络。
A . A. A. 单层无反馈 B . B. B. 多层有反馈 C . C. C. 多层无反馈
10、神经网络对信息的存储依赖( B B B)。
A . A. A. 神经元 B . B. B. 权系数 C . C. C. 网络节点
11、模糊均值聚类算法在求子类均值时,( B B B)参与运算。
A . A. A. 仅属于子类的样本 B . B. B. 所有样本 C . C. C. 没有样本
12、在蚁群算法中,信息素增量 Δ τ i j k ( t ) \Delta{\tau_{ij}}^k(t) Δτijk(t) 采用( A A A)时,称为蚁周系统或模型,这里, k k k 为第 k k k 只蚂蚁, Q Q Q 为常量, L k L_k Lk 为第 k k k 只蚂蚁走的路径长度, d i j d_{ij} dij 表示由 i i i 到 j j j 的边的长度。
A . A. A. Q / L k Q/L_k Q/Lk B . B. B. Q Q Q C . C. C. Q / d i j Q/d_{ij} Q/dij
三、解答题
(1)设有两类样本
ω 1 = { x 1 , x 2 } , x 1 = ( 1 , 0 , 1 ) T , x 2 = ( 0 , 1 , 1 ) T ; \omega_1=\{x_1,x_2\}, x_1 =(1,0,1)^T, x_2 =(0,1,1)^T; ω1={x1,x2},x1=(1,0,1)T,x2=(0,1,1)T;
ω 2 = { x 3 , x 4 } , x 3 = ( 1 , 1 , 0 ) T , x 4 = ( 0 , 1 , 0 ) T . \omega_2=\{x_3,x_4\},x_3=(1,1,0)^T,x_4 =(0,1,0)^T. ω2={x3,x4},x3=(1,1,0)T,x4=(0,1,0)T.
试用感知器算法,求出其分类用的线性判别函数。
解:增广规范化: x 1 = ( 1 , 0 , 1 , 1 ) T , x 2 = ( 0 , 1 , 1 , 1 ) T , x 3 = ( − 1 , − 1 , 0 , − 1 ) T , x 4 = ( 0 , − 1 , 0 , − 1 ) T x_1=(1,0,1,1)^T,x_2=(0,1,1,1)^T,x_3=(-1,-1,0,-1)^T,x_4=(0,-1,0,-1)^T x1=(1,0,1,1)T,x2=(0,1,1,1)T,x3=(−1,−1,0,−1)T,x4=(0,−1,0,−1)T,
设 W 1 = ( 1 , 1 , 1 , 1 ) T , c = 1 W_1=(1,1,1,1)^T,c=1 W1=(1,1,1,1)T,c=1
W 1 T x 1 = 3 > 0 {W_1}^Tx_1=3>0 W1Tx1=3>0
W 1 T x 2 = 3 > 0 {W_1}^Tx_2=3>0 W1Tx2=3>0
W 1 T x 3 = − 3 < 0 {W_1}^Tx_3=-3<0 W1Tx3=−3<0 修正
W 2 = W 1 + x 3 = ( 0 , 0 , 1 , 0 ) T W_2=W_1+x_3=(0,0,1,0)^T W2=W1+x3=(0,0,1,0)T
W 2 T x 4 = 0 {W_2}^Tx_4=0 W2Tx4=0 修正
W 3 = W 2 + x 4 = ( 0 , − 1 , 1 , − 1 ) T W_3=W_2+x_4=(0,-1,1,-1)^T W3=W2+x4=(0,−1,1,−1)T
W 3 T x 1 = 0 {W_3}^Tx_1=0 W3Tx1=0 修正
W 4 = W 3 + x 1 = ( 1 , − 1 , 2 , 0 ) T W_4=W_3+x_1=(1,-1,2,0)^T W4=W3+x1=(1,−1,2,0)T
W 4 T x 3 = 0 {W_4}^Tx_3=0 W4Tx3=0 修正
W 5 = W 4 + x 3 = ( 0 , − 2 , 2 , − 1 ) T W_5=W_4+x_3=(0,-2,2,-1)^T W5=W4+x3=(0,−2,2,−1)T
W 5 T x 2 = − 3 < 0 {W_5}^Tx_2=-3<0 W5Tx2=−3<0 修正
W 6 = W 5 + x 2 = ( 0 , − 1 , 3 , 0 ) T W_6=W_5+x_2=(0,-1,3,0)^T W6=W5+x2=(0,−1,3,0)T
训练结束, W = W 6 = ( 0 , − 1 , 3 , 0 ) W=W_6=(0,-1,3,0) W=W6=(0,−1,3,0)
线性判别函数为 d ( X ) = W T X = − x 2 + 3 X 3 d(X)=W^TX=-x_2+3X_3 d(X)=WTX=−x2+3X3
(2)已知有两类数据,分别为 ω 1 : ( 1 , 0 ) T , ( 2 , 0 ) T , ( 1 , 1 ) T ; ω 2 : ( − 1 , 0 ) T , ( 0 , 1 ) T , ( − 1 , 1 ) T \omega_1:(1,0)^T,(2,0)^T,(1,1)^T;\omega_2:(-1,0)^T,(0,1)^T,(-1,1)^T ω1:(1,0)T,(2,0)T,(1,1)T;ω2:(−1,0)T,(0,1)T,(−1,1)T
试求:该组数据的类内及类间离散矩阵 S ω S_\omega Sω 及 S b S_b Sb 。
解: m 1 = ( 4 3 , 1 3 ) T , m 2 = ( − 2 3 , 2 3 ) T m_1=(\frac{4}{3},\frac{1}{3})^T,m_2=(-\frac{2}{3},\frac{2}{3})^T m1=(34,31)T,m2=(−32,32)T
S 1 = ∑ x ∈ ω 1 ( x − m 1 ) ( x − m 1 ) T = ( 2 3 − 1 3 − 1 3 2 3 ) S_1=\sum\limits_{x\in \omega_1}(x-m_1)(x-m_1)^T=\left(\begin{matrix}\frac{2}{3}&-\frac{1}{3}\\-\frac{1}{3}&\frac{2}{3}\end{matrix}\right) S1=x∈ω1∑(x−m1)(x−m1)T=(32−31−3132),
S 2 = ∑ x ∈ ω 2 ( x − m 2 ) ( x − m 2 ) T = ( 2 3 1 3 1 3 2 3 ) S_2=\sum\limits_{x\in \omega_2}(x-m_2)(x-m_2)^T=\left(\begin{matrix}\frac{2}{3}&\frac{1}{3}\\\frac{1}{3}&\frac{2}{3}\end{matrix}\right) S2=x∈ω2∑(x−m2)(x−m2)T=(32313132),
S ω = 1 2 ( S 1 + S 2 ) = ( 2 3 0 0 2 3 ) S_\omega=\frac{1}{2}(S_1+S_2)=\left(\begin{matrix}\frac{2}{3}&0\\0&\frac{2}{3}\end{matrix}\right) Sω=21(S1+S2)=(320032),
S b = ( m 1 − m 2 ) ( m 1 − m 2 ) T = ( 2 − 1 3 ) ( 2 − 1 3 ) = ( 4 − 2 3 − 2 3 1 9 ) S_b=(m_1-m_2)(m_1-m_2)^T=\left(\begin{matrix}2\\-\frac{1}{3}\end{matrix}\right)\left(\begin{matrix}2&-\frac{1}{3}\end{matrix}\right)=\left(\begin{matrix}4&-\frac{2}{3}\\-\frac{2}{3}&\frac{1}{9}\end{matrix}\right) Sb=(m1−m2)(m1−m2)T=(2−31)(2−31)=(4−32−3291)。
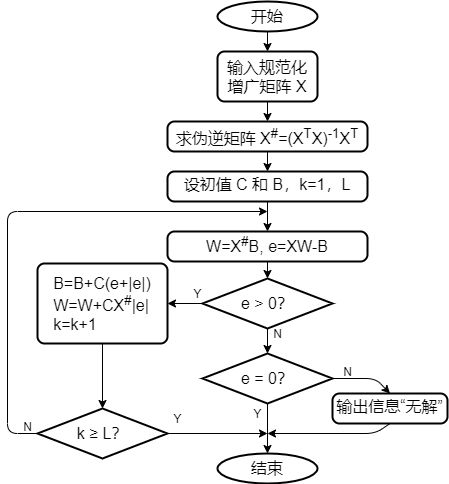
(3)设有两类样本: ω 1 = { ( 0 , 0 ) T , ( 0 , 1 ) T } , ω 2 = { ( 1 , 0 ) T , ( 1 , 1 ) T } . \omega_1 =\{(0,0)^T,(0,1)^T\}, \omega_2 =\{(1,0)^T,(1,1)^T\}. ω1={(0,0)T,(0,1)T},ω2={(1,0)T,(1,1)T}.
试画出何-卡氏算法求其线性判别函数的流程图,并求出该函数。
解:
X = ( 0 0 1 0 1 1 − 1 0 − 1 − 1 − 1 − 1 ) , X # = ( X T X ) − 1 X T = 1 4 ( − 2 − 2 − 2 − 2 − 2 2 2 − 2 3 1 − 1 1 ) X=\left(\begin{matrix}0&0&1\\0&1&1\\-1&0&-1\\-1&-1&-1\end{matrix}\right),X^\#=(X^TX)^{-1}X^T=\frac{1}{4}\left(\begin{matrix}-2&-2&-2&-2\\-2&2&2&-2\\3&1&-1&1\end{matrix}\right) X=⎝⎜⎜⎛00−1−1010−111−1−1⎠⎟⎟⎞,X#=(XTX)−1XT=41⎝⎛−2−23−221−22−1−2−21⎠⎞,
取 校正增量 c = 1 c=1 c=1,迭代次数 k = 1 , B 1 = ( 1 , 1 , 1 , 1 ) T k=1,B_1=(1,1,1,1)^T k=1,B1=(1,1,1,1)T,
W 1 = X # B 1 = ( − 2 , 0 , 1 ) T W_1=X^\#B_1=(-2,0,1)^T W1=X#B1=(−2,0,1)T,
e 1 = X W 1 − B 1 = ( 0 0 0 0 ) = 0 → e_1=XW_1-B_1=\left(\begin{matrix}0\\0\\0\\0\end{matrix}\right)=\overrightarrow{0} e1=XW1−B1=⎝⎜⎜⎛0000⎠⎟⎟⎞=0,
所以 W 1 W_1 W1 为所求解,系统线性可分,判别函数 d ( X ) = W T ( x 1 , x 2 , 1 ) T = − 2 x 1 + 1 d(X)=W^T(x_1,x_2,1)^T=-2x_1+1 d(X)=WT(x1,x2,1)T=−2x1+1。
(4)有训练集资料矩阵如下表所示,现已知, N = 9 , N 1 = N 2 = N 3 = 3 , n = 2 , M = 3 N=9,N_1=N_2=N_3=3,n=2,M=3 N=9,N1=N2=N3=3,n=2,M=3。
| 训练样本号k | 1 2 3 | 1 2 3 | 1 2 3 |
|---|---|---|---|
| 特征 x 1 x_1 x1 | 0 1 2 | -2 -1 -2 | 0 1 -1 |
| 特征 x 2 x_2 x2 | 1 -1 1 | 1 0 -1 | -1 -2 -2 |
| 类别 | ω 1 \omega_1 ω1 | ω 2 \omega_2 ω2 | ω 3 \omega_3 ω3 |
假定三类协方差不等,每一类都符合正态分布,
先验概率 P ( ω 1 ) = P ( ω 2 ) = P ( ω 3 ) = 1 3 P(\omega_1)=P(\omega_2)=P(\omega_3)=\frac{1}{3} P(ω1)=P(ω2)=P(ω3)=31,
多类判别函数 g i ( X ) = X T W i X + ω i T X + ω i 0 g_i(X)=X^TW_iX+{\omega_i}^TX+\omega_{i0} gi(X)=XTWiX+ωiTX+ωi0,
其中, W i = − 1 2 ∑ i − 1 , ω i = ∑ i − 1 μ i , ω i 0 = − 1 2 μ i T ∑ i − 1 μ i − 1 2 ln ∣ ∑ i ∣ + ln P ( ω i ) W_i=-\frac{1}{2}{\sum_{i}}^{-1},\omega_i={\sum_{i}}^{-1}\mu_i,\omega_{i0}=-\frac{1}{2}{\mu_i}^T{\sum_{i}}^{-1}\mu_i-\frac{1}{2}\ln|\sum_i|+\ln P(\omega_i) Wi=−21∑i−1,ωi=∑i−1μi,ωi0=−21μiT∑i−1μi−21ln∣∑i∣+lnP(ωi)。
试先求出每一类的判别函数,然后判断未知样本 x = ( 1 , 1 ) T x=(1,1)^T x=(1,1)T 应属于哪一类?
解: μ 1 = ( 1 , 1 3 ) T , μ 2 = ( − 5 3 , 0 ) T , μ 3 = ( 0 , − 5 3 ) T \mu_1=(1,\frac{1}{3})^T,\mu_2=(-\frac{5}{3},0)^T,\mu_3=(0,-\frac{5}{3})^T μ1=(1,31)T,μ2=(−35,0)T,μ3=(0,−35)T,
∑ 1 = 1 3 − 1 [ ( − 1 2 3 ) ( − 1 2 3 ) + ( 0 − 4 3 ) ( 0 − 4 3 ) + ( 1 2 3 ) ( 1 2 3 ) ] = ( 1 0 0 4 3 ) \sum_1=\frac{1}{3-1}[\left(\begin{matrix}-1\\\frac{2}{3}\end{matrix}\right)(-1 \frac{2}{3})+\left(\begin{matrix}0\\-\frac{4}{3}\end{matrix}\right)(0 -\frac{4}{3})+\left(\begin{matrix}1\\\frac{2}{3}\end{matrix}\right)(1 \frac{2}{3})]=\left(\begin{matrix}1&0\\0&\frac{4}{3}\end{matrix}\right) ∑1=3−11[(−132)(−1 32)+(0−34)(0 −34)+(132)(1 32)]=(10034),
∑ 2 = 1 3 − 1 [ ( − 1 3 1 ) ( − 1 3 1 ) + ( 2 3 0 ) ( 2 3 0 ) + ( − 1 3 − 1 ) ( − 1 3 − 1 ) ] = ( 1 3 0 0 1 ) \sum_2=\frac{1}{3-1}[\left(\begin{matrix}-\frac{1}{3}\\1\end{matrix}\right)(-\frac{1}{3} 1)+\left(\begin{matrix}\frac{2}{3}\\0\end{matrix}\right)(\frac{2}{3} 0)+\left(\begin{matrix}-\frac{1}{3}\\-1\end{matrix}\right)(-\frac{1}{3} -1)]=\left(\begin{matrix}\frac{1}{3}&0\\0&1\end{matrix}\right) ∑2=3−11[(−311)(−31 1)+(320)(32 0)+(−31−1)(−31 −1)]=(31001),
∑ 3 = 1 3 − 1 [ ( 0 2 3 ) ( 0 2 3 ) + ( 1 − 1 3 ) ( 1 − 1 3 ) + ( − 1 − 1 3 ) ( − 1 − 1 3 ) ] = ( 1 0 0 1 3 ) \sum_3=\frac{1}{3-1}[\left(\begin{matrix}0\\\frac{2}{3}\end{matrix}\right)(0 \frac{2}{3})+\left(\begin{matrix}1\\-\frac{1}{3}\end{matrix}\right)(1 -\frac{1}{3})+\left(\begin{matrix}-1\\-\frac{1}{3}\end{matrix}\right)(-1 -\frac{1}{3})]=\left(\begin{matrix}1&0\\0&\frac{1}{3}\end{matrix}\right) ∑3=3−11[(032)(0 32)+(1−31)(1 −31)+(−1−31)(−1 −31)]=(10031),
g 1 ( X ) = X T W 1 X + ω 1 T X + ω 10 = − 1 2 ( x 1 2 + 3 4 x 2 2 ) + x 1 + 1 4 x 2 − 1.7841 g_1(X)=X^TW_1X+{\omega_1}^TX+\omega_{10}=-\frac{1}{2}({x_1}^2+\frac{3}{4}{x_2}^2)+x_1+\frac{1}{4}x_2-1.7841 g1(X)=XTW1X+ω1TX+ω10=−21(x12+43x22)+x1+41x2−1.7841,
g 2 ( X ) = X T W 2 X + ω 2 T X + ω 20 = − 1 2 ( 3 x 1 2 + x 2 2 ) − 5 x 1 − 5.2653 g_2(X)=X^TW_2X+{\omega_2}^TX+\omega_{20}=-\frac{1}{2}(3{x_1}^2+{x_2}^2)-5x_1-5.2653 g2(X)=XTW2X+ω2TX+ω20=−21(3x12+x22)−5x1−5.2653,
g 3 ( X ) = X T W 3 X + ω 3 T X + ω 30 = − 1 2 ( x 1 2 + 3 x 2 2 ) + x 1 − 5 3 x 2 − 4.176 g_3(X)=X^TW_3X+{\omega_3}^TX+\omega_{30}=-\frac{1}{2}({x_1}^2+3{x_2}^2)+x_1-\frac{5}{3}x_2-4.176 g3(X)=XTW3X+ω3TX+ω30=−21(x12+3x22)+x1−35x2−4.176,
将 x = ( 1 , 1 ) T x=(1,1)^T x=(1,1)T 代入, g 1 ( x ) = − 1.4091 , g 2 ( x ) = − 12.2653 , g 3 ( x ) = − 11.7160 g_1(x)=-1.4091,g_2(x)=-12.2653,g_3(x)=-11.7160 g1(x)=−1.4091,g2(x)=−12.2653,g3(x)=−11.7160,
g 1 ( x ) g_1(x) g1(x) 最大,判 x = ( 1 , 1 ) T ∈ ω 1 x=(1,1)^T\in \omega_1 x=(1,1)T∈ω1。
(5)已知正常细胞先验概率为 P ( ω 1 ) = 0.9 P(\omega_1)=0.9 P(ω1)=0.9, 异常为 P ( ω 2 ) = 0.1 P(\omega_2)=0.1 P(ω2)=0.1,
从类条件概率密度分布曲线上查的 p ( x ∣ ω 1 ) = 0.3 , p ( x ∣ ω 2 ) = 0.5 , λ 11 = 0 , λ 21 = 7 , λ 12 = 2 , λ 22 = 0 p(x|\omega_1)=0.3,p(x|\omega_2)=0.5,\lambda_{11}=0,\lambda_{21}=7,\lambda_{12}=2,\lambda_{22}=0 p(x∣ω1)=0.3,p(x∣ω2)=0.5,λ11=0,λ21=7,λ12=2,λ22=0
条件风险: R ( ω i ∣ x ) = ∑ j = 1 2 λ i j P ( ω j ∣ x ) R(\omega_i|x)=\sum\limits_{j=1}^{2}\lambda_{ij}P(\omega_j|x) R(ωi∣x)=j=1∑2λijP(ωj∣x),
试按条件风险最小来决定 x x x 所属的类别。
解: P ( x ) = P ( x ∣ ω 1 ) P ( ω 1 ) + P ( x ∣ ω 2 ) P ( ω 2 ) = 0.27 + 0.05 = 0.32 P(x)=P(x|\omega_1)P(\omega_1)+P(x|\omega_2)P(\omega_2)=0.27+0.05=0.32 P(x)=P(x∣ω1)P(ω1)+P(x∣ω2)P(ω2)=0.27+0.05=0.32,
P ( ω 1 ∣ x ) = P ( x ∣ ω 1 ) P ( ω 1 ) P ( x ) = 0.844 P(\omega_1|x)=\frac{P(x|\omega_1)P(\omega_1)}{P(x)}=0.844 P(ω1∣x)=P(x)P(x∣ω1)P(ω1)=0.844,
P ( ω 2 ∣ x ) = P ( x ∣ ω 2 ) P ( ω 2 ) P ( x ) = 0.156 P(\omega_2|x)=\frac{P(x|\omega_2)P(\omega_2)}{P(x)}= 0.156 P(ω2∣x)=P(x)P(x∣ω2)P(ω2)=0.156,
R ( ω 1 ∣ x ) = 0 + 2 ∗ 0.156 = 0.312 R(\omega_1|x)=0+2*0.156=0.312 R(ω1∣x)=0+2∗0.156=0.312,
R ( ω 2 ∣ x ) = 7 ∗ 0.844 + 0 = 5.908 R(\omega_2|x)=7*0.844+0=5.908 R(ω2∣x)=7∗0.844+0=5.908。
所以,按条件风险最小的原则, x x x 应判为属于第一类。
(6)设两个集群的数据分别为 ( 1 , 0 ) T , ( 2 , 0 ) T , ( 1 , 1 ) T {(1,0)^T,(2,0)^T,(1,1)^T} (1,0)T,(2,0)T,(1,1)T与 ( 0 , 1 ) T , ( − 1 , 0 ) T , ( − 1 , 1 ) T {(0,1)^T,(-1,0)^T,(-1,1)^T} (0,1)T,(−1,0)T,(−1,1)T。
试求:
1) 两个集群的均值。
2) 若将数据 ( 1 , 1 ) T (1,1)^T (1,1)T 从第一个集群转移至第二个集群时,准则函数值 J J J (每个样本与其所在集群均值点的距离平方和)的变化量。
解:
1) m 1 = ( 4 3 , 1 3 ) T , m 2 = ( − 2 3 , 2 3 ) T m_1=(\frac{4}{3},\frac{1}{3})^T,m_2=(-\frac{2}{3},\frac{2}{3})^T m1=(34,31)T,m2=(−32,32)T。
2) J 0 = ∑ i = 1 c ∑ x ∈ ω i ∣ ∣ x − m i ∣ ∣ 2 \begin{aligned}J_0&=\sum\limits_{i=1}^{c}\sum\limits_{x\in \omega_i}{||x-m_i||}^2\end{aligned} J0=i=1∑cx∈ωi∑∣∣x−mi∣∣2, c c c 为类数。
( 1 , 1 ) T (1,1)^T (1,1)T 从第一个集群中移出,准则函数值减少为 3 3 − 1 ∣ ∣ ( 1 , 1 ) T − ( 4 3 , 1 3 ) T ∣ ∣ 2 = 5 6 \frac{3}{3-1}||(1,1)^T-(\frac{4}{3},\frac{1}{3})^T||^2=\frac{5}{6} 3−13∣∣(1,1)T−(34,31)T∣∣2=65,
该数据加入第二个集群,准则函数值增加为 3 3 + 1 ∣ ∣ ( 1 , 1 ) T − ( − 2 3 , 2 3 ) T ∣ ∣ 2 = 13 6 \frac{3}{3+1}||(1,1)^T-(-\frac{2}{3},\frac{2}{3})^T||^2=\frac{13}{6} 3+13∣∣(1,1)T−(−32,32)T∣∣2=613。
准则函数值增加量为 4 3 \frac{4}{3} 34,不宜转。
(7)若数据集共有 m m m 个类 ω 1 , ω 2 , ⋅ ⋅ ⋅ , ω m \omega_1,\omega_2,···,\omega_m ω1,ω2,⋅⋅⋅,ωm,总离散矩阵为 S ω S_\omega Sω
1 ) 试求证某一数据 x x x 从 ω i \omega_i ωi 转移至 ω j \omega_j ωj 类时, ω i \omega_i ωi 的散布矩阵的变化量为 − N i N i − 1 ( x − m i ) ( x − m i ) T -\frac{N_i}{N_i-1}(x-m_i)(x-m_i)^T −Ni−1Ni(x−mi)(x−mi)T 其中 m i m_i mi 是转移前类 τ i \tau_i τi 的均值向量, N i N_i Ni 是转移前 ω i \omega_i ωi 的数据量。
2)推测 ω j \omega_j ωj 在增加数据 x x x 后其散布矩阵的变化量。
3)计算总散布矩阵的变化量。
解:
m i ′ = 1 N i − 1 ( m i ∗ N i − x ) = 1 N i − 1 [ ( N i − 1 ) m i + m i − x ] = m i + 1 N i − 1 ( m i − x ) \begin{aligned}{m_i}^{'}&=\frac{1}{N_i-1}(m_i*N_i-x)=\frac{1}{N_i-1}[(N_i-1)m_i+m_i-x]\\&=m_i+\frac{1}{N_i-1}(m_i-x)\end{aligned} mi′=Ni−11(mi∗Ni−x)=Ni−11[(Ni−1)mi+mi−x]=mi+Ni−11(mi−x)
按离散矩阵的定义计算,可得 τ i \tau_i τi 的离散矩阵变化前后的关系为:
S i ′ = S i − N i N i − 1 ( x − m i ) ( x − m i ) T {S_i}^{'}=S_i-\frac{N_i}{N_i-1}(x-m_i)(x-m_i)^T Si′=Si−Ni−1Ni(x−mi)(x−mi)T,
2)同理,可计算 τ j \tau_j τj 的离散矩阵变化前后的关系为:
S j ′ = S j + N i N i − 1 ( x − m j ) ( x − m j ) T {S_j}^{'}=S_j+\frac{N_i}{N_i-1}(x-m_j)(x-m_j)^T Sj′=Sj+Ni−1Ni(x−mj)(x−mj)T,
3)故总的离散矩阵变化前后的关系为:
S ω ′ = S ω − N i N i − 1 ( x − m i ) ( x − m i ) T + N j N j − 1 ( x − m j ) ( x − m j ) T {S_\omega}^{'}=S_\omega-\frac{N_i}{N_i-1}(x-m_i)(x-m_i)^T+\frac{N_j}{N_j-1}(x-m_j)(x-m_j)^T Sω′=Sω−Ni−1Ni(x−mi)(x−mi)T+Nj−1Nj(x−mj)(x−mj)T。
(8)已知有 5 5 5 个样本,每个样本有 2 2 2 个特征,类型数目 M = 2 M=2 M=2,数据如下:
| 样本序号 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 特征 x 1 x_1 x1 | 0 | 1 | 3 | 6 | 7 |
| 特征 x 2 x_2 x2 | 0 | 0 | 2 | 6 | 6 |
试用 K − K- K−均值算法找聚类中心,并对它们进行聚类。
解:先设 Z 1 ( 1 ) = ( 0 , 0 ) T , Z 2 ( 1 ) = ( 1 , 0 ) T Z_1(1)=(0,0)^T,Z_2(1)=(1,0)^T Z1(1)=(0,0)T,Z2(1)=(1,0)T,
∣ ∣ x 3 − Z 1 ( 1 ) ∣ ∣ > ∣ ∣ x 3 − Z 2 ( 1 ) ∣ ∣ ||x_3-Z_1(1)||>||x_3-Z_2(1)|| ∣∣x3−Z1(1)∣∣>∣∣x3−Z2(1)∣∣,
∣ ∣ x 4 − Z 1 ( 1 ) ∣ ∣ > ∣ ∣ x 4 − Z 2 ( 1 ) ∣ ∣ ||x_4-Z_1(1)||>||x_4-Z_2(1)|| ∣∣x4−Z1(1)∣∣>∣∣x4−Z2(1)∣∣,
∣ ∣ x 5 − Z 1 ( 1 ) ∣ ∣ > ∣ ∣ x 5 − Z 2 ( 1 ) ∣ ∣ ||x_5-Z_1(1)||>||x_5-Z_2(1)|| ∣∣x5−Z1(1)∣∣>∣∣x5−Z2(1)∣∣,
分为两类 ω 1 : x 1 ; ω 2 : x 2 , x 3 , x 4 , x 5 \omega_1:x_1;\omega_2:x_2,x_3,x_4,x_5 ω1:x1;ω2:x2,x3,x4,x5
Z 1 ( 2 ) = ( 0 , 0 ) T , Z 2 ( 2 ) = ( 17 4 , 7 2 ) T Z_1(2)=(0,0)^T,Z_2(2)=(\frac{17}{4},\frac{7}{2})^T Z1(2)=(0,0)T,Z2(2)=(417,27)T,
∣ ∣ x 1 − Z 1 ( 2 ) ∣ ∣ < ∣ ∣ x 1 − Z 2 ( 2 ) ∣ ∣ ||x_1-Z_1(2)||<||x_1-Z_2(2)|| ∣∣x1−Z1(2)∣∣<∣∣x1−Z2(2)∣∣,
∣ ∣ x 2 − Z 1 ( 2 ) ∣ ∣ < ∣ ∣ x 2 − Z 2 ( 2 ) ∣ ∣ ||x_2-Z_1(2)||<||x_2-Z_2(2)|| ∣∣x2−Z1(2)∣∣<∣∣x2−Z2(2)∣∣,
∣ ∣ x 3 − Z 1 ( 2 ) ∣ ∣ > ∣ ∣ x 3 − Z 2 ( 2 ) ∣ ∣ ||x_3-Z_1(2)||>||x_3-Z_2(2)|| ∣∣x3−Z1(2)∣∣>∣∣x3−Z2(2)∣∣,
∣ ∣ x 4 − Z 1 ( 2 ) ∣ ∣ > ∣ ∣ x 4 − Z 2 ( 2 ) ∣ ∣ ||x_4-Z_1(2)||>||x_4-Z_2(2)|| ∣∣x4−Z1(2)∣∣>∣∣x4−Z2(2)∣∣,
∣ ∣ x 5 − Z 1 ( 2 ) ∣ ∣ > ∣ ∣ x 5 − Z 2 ( 2 ) ∣ ∣ ||x_5-Z_1(2)||>||x_5-Z_2(2)|| ∣∣x5−Z1(2)∣∣>∣∣x5−Z2(2)∣∣,
分为两类 ω 1 : x 1 , x 2 ; ω 2 : x 3 , x 4 , x 5 \omega_1:x_1,x_2;\omega_2:x_3,x_4,x_5 ω1:x1,x2;ω2:x3,x4,x5
Z 1 ( 3 ) = ( 1 2 , 0 ) T , Z 2 ( 3 ) = ( 16 3 , 14 3 ) T Z_1(3)=(\frac{1}{2},0)^T,Z_2(3)=(\frac{16}{3},\frac{14}{3})^T Z1(3)=(21,0)T,Z2(3)=(316,314)T,
∣ ∣ x 1 − Z 1 ( 3 ) ∣ ∣ < ∣ ∣ x 1 − Z 2 ( 3 ) ∣ ∣ ||x_1-Z_1(3)||<||x_1-Z_2(3)|| ∣∣x1−Z1(3)∣∣<∣∣x1−Z2(3)∣∣,
∣ ∣ x 2 − Z 1 ( 3 ) ∣ ∣ < ∣ ∣ x 2 − Z 2 ( 3 ) ∣ ∣ ||x_2-Z_1(3)||<||x_2-Z_2(3)|| ∣∣x2−Z1(3)∣∣<∣∣x2−Z2(3)∣∣,
∣ ∣ x 3 − Z 1 ( 3 ) ∣ ∣ < ∣ ∣ x 3 − Z 2 ( 3 ) ∣ ∣ ||x_3-Z_1(3)||<||x_3-Z_2(3)|| ∣∣x3−Z1(3)∣∣<∣∣x3−Z2(3)∣∣,
∣ ∣ x 4 − Z 1 ( 3 ) ∣ ∣ > ∣ ∣ x 4 − Z 2 ( 3 ) ∣ ∣ ||x_4-Z_1(3)||>||x_4-Z_2(3)|| ∣∣x4−Z1(3)∣∣>∣∣x4−Z2(3)∣∣,
∣ ∣ x 5 − Z 1 ( 3 ) ∣ ∣ > ∣ ∣ x 5 − Z 2 ( 3 ) ∣ ∣ ||x_5-Z_1(3)||>||x_5-Z_2(3)|| ∣∣x5−Z1(3)∣∣>∣∣x5−Z2(3)∣∣,
分为两类 ω 1 : x 1 , x 2 , x 3 ; ω 2 : x 4 , x 5 \omega_1:x_1,x_2,x_3;\omega_2:x_4,x_5 ω1:x1,x2,x3;ω2:x4,x5
Z 1 ( 4 ) = ( 4 3 , 2 3 ) T , Z 2 ( 4 ) = ( 13 2 , 6 ) T Z_1(4)=(\frac{4}{3},\frac{2}{3})^T,Z_2(4)=(\frac{13}{2},6)^T Z1(4)=(34,32)T,Z2(4)=(213,6)T,
∣ ∣ x 1 − Z 1 ( 4 ) ∣ ∣ < ∣ ∣ x 1 − Z 2 ( 4 ) ∣ ∣ ||x_1-Z_1(4)||<||x_1-Z_2(4)|| ∣∣x1−Z1(4)∣∣<∣∣x1−Z2(4)∣∣,
∣ ∣ x 2 − Z 1 ( 4 ) ∣ ∣ < ∣ ∣ x 2 − Z 2 ( 4 ) ∣ ∣ ||x_2-Z_1(4)||<||x_2-Z_2(4)|| ∣∣x2−Z1(4)∣∣<∣∣x2−Z2(4)∣∣,
∣ ∣ x 3 − Z 1 ( 4 ) ∣ ∣ < ∣ ∣ x 3 − Z 2 ( 4 ) ∣ ∣ ||x_3-Z_1(4)||<||x_3-Z_2(4)|| ∣∣x3−Z1(4)∣∣<∣∣x3−Z2(4)∣∣,
∣ ∣ x 4 − Z 1 ( 4 ) ∣ ∣ > ∣ ∣ x 4 − Z 2 ( 4 ) ∣ ∣ ||x_4-Z_1(4)||>||x_4-Z_2(4)|| ∣∣x4−Z1(4)∣∣>∣∣x4−Z2(4)∣∣,
∣ ∣ x 5 − Z 1 ( 4 ) ∣ ∣ > ∣ ∣ x 5 − Z 2 ( 4 ) ∣ ∣ ||x_5-Z_1(4)||>||x_5-Z_2(4)|| ∣∣x5−Z1(4)∣∣>∣∣x5−Z2(4)∣∣,
分为两类 ω 1 : x 1 , x 2 , x 3 ; ω 2 : x 4 , x 5 \omega_1:x_1,x_2,x_3;\omega_2:x_4,x_5 ω1:x1,x2,x3;ω2:x4,x5
Z 1 ( 5 ) = ( 4 3 , 2 3 ) T , Z 2 ( 5 ) = ( 13 2 , 6 ) T , Z 1 ( 5 ) = Z 1 ( 4 ) , Z 2 ( 5 ) = Z 2 ( 4 ) Z_1(5)=(\frac{4}{3},\frac{2}{3})^T,Z_2(5)=(\frac{13}{2},6)^T,Z_1(5)=Z_1(4),Z_2(5)=Z_2(4) Z1(5)=(34,32)T,Z2(5)=(213,6)T,Z1(5)=Z1(4),Z2(5)=Z2(4),
故聚类结束,两聚类中心为 m 1 = ( 4 3 , 2 3 ) T , m 2 = ( 13 2 , 6 ) T , ω 1 : x 1 , x 2 , x 3 ; ω 2 : x 4 , x 5 m_1=(\frac{4}{3},\frac{2}{3})^T,m_2=(\frac{13}{2},6)^T,\omega_1:x_1,x_2,x_3;\omega_2:x_4,x_5 m1=(34,32)T,m2=(213,6)T,ω1:x1,x2,x3;ω2:x4,x5。
(9)若有下列两类样本:
| 训练样本号k | 1 2 3 4 | 1 2 3 4 |
|---|---|---|
| 特征 x 1 x_1 x1 | 0 1 1 1 | 0 0 0 1 |
| 特征 x 2 x_2 x2 | 0 0 0 1 | 0 1 1 1 |
| 特征 x 3 x_3 x3 | 0 0 1 0 | 1 0 1 1 |
| 类别 | ω 1 \omega_1 ω1 | ω 2 \omega_2 ω2 |
-
试用 K − L K-L K−L 变换,将其降到 1 1 1 维特征空间;
-
求其最佳鉴别 F i s h e r Fisher Fisher 矢量 W = S ω − 1 ( m 1 − m 2 ) W={S_\omega}^{-1}(m_1-m_2) W=Sω−1(m1−m2) 及 F i s h e r Fisher Fisher 判别函数。
解:
1)
E ( X X T ) = 1 8 [ ( 0 1 1 1 0 0 0 1 0 0 1 0 ) ( 0 0 0 1 0 0 1 0 1 1 1 0 ) + ( 0 0 0 1 0 1 1 1 1 0 1 1 ) ( 0 0 1 0 1 0 0 1 1 1 1 1 ) ] = ( 1 2 1 4 1 4 1 4 1 2 1 4 1 4 1 4 1 2 ) \begin{aligned}E(XX^T)&=\frac{1}{8}[\left(\begin{matrix}0&1&1&1\\0&0&0&1\\0&0&1&0\end{matrix}\right)\left(\begin{matrix}0&0&0\\1&0&0\\1&0&1\\1&1&0\end{matrix}\right)+\left(\begin{matrix}0&0&0&1\\0&1&1&1\\1&0&1&1\end{matrix}\right)\left(\begin{matrix}0&0&1\\0&1&0\\0&1&1\\1&1&1\end{matrix}\right)]\\&=\left(\begin{matrix}\frac{1}{2}&\frac{1}{4}&\frac{1}{4}\\\frac{1}{4}&\frac{1}{2}&\frac{1}{4}\\\frac{1}{4}&\frac{1}{4}&\frac{1}{2}\end{matrix}\right)\end{aligned} E(XXT)=81[⎝⎛000100101110⎠⎞⎝⎜⎜⎛011100010010⎠⎟⎟⎞+⎝⎛001010011111⎠⎞⎝⎜⎜⎛000101111011⎠⎟⎟⎞]=⎝⎛214141412141414121⎠⎞
λ = ( 1 4 0 0 0 1 4 0 0 0 1 ) , μ = ( 0 − 2 6 1 3 1 2 1 6 1 3 − 1 2 1 6 1 3 ) \lambda=\left(\begin{matrix}\frac{1}{4}&0&0\\0&\frac{1}{4}&0\\0&0&1\end{matrix}\right),\mu=\left(\begin{matrix}0&-\frac{2}{\sqrt6}&\frac{1}{\sqrt3}\\\frac{1}{\sqrt2}&\frac{1}{\sqrt6}&\frac{1}{\sqrt3}\\-\frac{1}{\sqrt2}&\frac{1}{\sqrt6}&\frac{1}{\sqrt3}\end{matrix}\right) λ=⎝⎛41000410001⎠⎞,μ=⎝⎜⎛021−21−626161313131⎠⎟⎞,
用最大特征根 λ = 1 \lambda=1 λ=1 的特征向量 μ 1 = 1 3 ( 1 , 1 , 1 ) T \mu_1=\frac{1}{\sqrt{3}}(1,1,1)^T μ1=31(1,1,1)T 将样本降到一维空间,
ω 1 : 0 1 3 2 3 2 3 \omega_1:0 \frac{1}{\sqrt3} \frac{2}{\sqrt3} \frac{2}{\sqrt3} ω1:0 31 32 32,
ω 2 : 1 3 1 3 2 3 3 3 \omega_2:\frac{1}{\sqrt3} \frac{1}{\sqrt3} \frac{2}{\sqrt3} \frac{3}{\sqrt3} ω2:31 31 32 33。
2) W = S ω − 1 ( m 1 − m 2 ) = ( 6 , − 6 , − 6 ) T W={S_\omega}^{-1}(m_1-m_2)=(6,-6,-6)^T W=Sω−1(m1−m2)=(6,−6,−6)T,
ω 1 : 0 , 6 , 0 , 0 ; ω 2 : − 6 , − 6 , − 12 , − 6 \omega_1:0,6,0,0;\omega_2:-6,-6,-12,-6 ω1:0,6,0,0;ω2:−6,−6,−12,−6,
y t = Y 1 ‾ + Y 2 ‾ 2 = W T X 1 ‾ + W T X 2 ‾ 2 = − 3 y_t=\frac{\overline{Y_1}+{\overline{Y_2}}}{2}=\frac{W^T\overline{X_1}+W^T\overline{X_2}}{2}=-3 yt=2Y1+Y2=2WTX1+WTX2=−3,
Y = W T X ⟹ 6 x 1 − 6 x 2 − 6 x 3 = − 3 ⟹ 2 x 1 − 2 x 2 − 2 x 3 = − 1 Y=W^TX\Longrightarrow 6x_1-6x_2-6x_3=-3\Longrightarrow 2x_1-2x_2-2x_3=-1 Y=WTX⟹6x1−6x2−6x3=−3⟹2x1−2x2−2x3=−1,
当 Y = W T X = 2 x 1 − 2 x 2 − 2 x 3 > − 1 Y=W^TX=2x_1-2x_2-2x_3>-1 Y=WTX=2x1−2x2−2x3>−1 时, X ∈ ω 1 X\in \omega_1 X∈ω1,
当 Y = W T X = 2 x 1 − 2 x 2 − 2 x 3 < − 1 Y=W^TX=2x_1-2x_2-2x_3<-1 Y=WTX=2x1−2x2−2x3<−1 时, X ∈ ω 2 X\in \omega_2 X∈ω2。
(10)如标准数字 1 1 1 在 7 ∗ 5 7*5 7∗5 的方格中表示成如图所示的黑白图像,黑为 1 1 1,白为 0 0 0,现若有一数字 1 1 1 在 7 ∗ 5 7*5 7∗5 网格中向左错了一列。试用分别计算要与标准模板之间的欧氏距离、绝对值偏差、偏差的夹角表示,以及用“异或”计算两者差异。

解: X = ( 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 ) , X 1 = ( 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 ) X=\left(\begin{matrix}0&0&1&0&0\\0&0&1&0&0\\0&0&1&0&0\\0&0&1&0&0\\0&0&1&0&0\\0&0&1&0&0\\0&0&1&0&0\end{matrix}\right),X^1=\left(\begin{matrix}0&1&0&0&0\\0&1&0&0&0\\0&1&0&0&0\\0&1&0&0&0\\0&1&0&0&0\\0&1&0&0&0\\0&1&0&0&0\end{matrix}\right) X=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛00000000000000111111100000000000000⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞,X1=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎛00000001111111000000000000000000000⎠⎟⎟⎟⎟⎟⎟⎟⎟⎞。
∣ ∣ X − X 1 ∣ ∣ = 14 ||X-X^1||=\sqrt{14} ∣∣X−X1∣∣=14(欧氏距离)
∣ X − X 1 ∣ = 14 |X-X^1|=14 ∣X−X1∣=14(绝对值偏差)
S ( X , X 1 ) = X T X 1 ∣ ∣ X T ∣ ∣ ∣ ∣ X 1 ∣ ∣ = 0 ⟹ θ = 90 ∘ S(X,X^1)=\frac{X^TX^1}{||X^T||||X^1||}=0\Longrightarrow \theta={90}^{\circ} S(X,X1)=∣∣XT∣∣∣∣X1∣∣XTX1=0⟹θ=90∘。
(11)设两类样本的类内离散矩阵分别为 S 1 = [ 1 1 2 1 2 1 ] S_1=\left[\begin{matrix}1&\frac{1}{2}\\\frac{1}{2}&1\end{matrix}\right] S1=[121211], S 2 = [ 1 − 1 2 − 1 2 1 ] S_2=\left[\begin{matrix}1&-\frac{1}{2}\\-\frac{1}{2}&1\end{matrix}\right] S2=[1−21−211], m 1 = ( 2 , 0 ) T , m 2 = ( 2 , 2 ) T m_1=(2,0)^T,m_2=(2,2)^T m1=(2,0)T,m2=(2,2)T,试用 f i s h e r fisher fisher 准则求其决策面方程。
解:
总类内离散度矩阵: S ω = 1 2 ( S 1 + S 2 ) = ( 1 0 0 1 ) S_\omega=\frac{1}{2}(S_1+S_2)=\left(\begin{matrix}1&0\\0&1\end{matrix}\right) Sω=21(S1+S2)=(1001),
F i s h e r Fisher Fisher 最佳投影方向: W ∗ = S ω − 1 ( m 1 − m 2 ) = ( 0 − 2 ) T W^*={S_\omega}^{-1}(m_1-m_2)=(0 -2)^T W∗=Sω−1(m1−m2)=(0 −2)T,
两类样本分布形状相同(只是方向不同),因此 y 0 y_0 y0 应为两类均值投影的中点:
y 0 = W ∗ T m 1 + m 2 2 = ( 0 − 2 ) ( 2 1 ) = − 2 y_0={W^*}^T\frac{m_1+m_2}{2}=(0 -2)\left(\begin{matrix}2\\1\end{matrix}\right)=-2 y0=W∗T2m1+m2=(0 −2)(21)=−2,
决策面方程 d ( X ) = W ∗ T X + 2 d(X)={W^*}^TX+2 d(X)=W∗TX+2,
最佳线性分界面 W ∗ T ( x 1 , x 2 ) T = − 2 ⟹ − 2 x 2 = − 2 ⟹ x 2 = 1 {W^*}^T(x_1,x_2)^T=-2\Longrightarrow -2x_2=-2\Longrightarrow x_2=1 W∗T(x1,x2