使用PyMC3建立GMM似然函数
1. GMM的似然函数
对于
K = 3 , μ = [ ( 1 , 1 ) ( 3 , 3 ) ( 5 , 5 ) ] , c o v = [ ( 1 − 0.8 − 0.8 1 ) ( 1 0.8 0.8 1 ) ( 1 − 0.8 − 0.8 1 ) ] K=3\ ,\ \mu=\begin{bmatrix} (1,1)\\(3,3)\\(5,5)\end{bmatrix}, cov=\begin{bmatrix}\begin{pmatrix}1&-0.8\\-0.8&1\end{pmatrix}\\\begin{pmatrix}1&0.8\\0.8&1\end{pmatrix}\\\begin{pmatrix}1&-0.8\\-0.8&1\end{pmatrix}\end{bmatrix} K=3 , μ=⎣⎡(1,1)(3,3)(5,5)⎦⎤,cov=⎣⎢⎢⎢⎢⎢⎢⎡(1−0.8−0.81)(10.80.81)(1−0.8−0.81)⎦⎥⎥⎥⎥⎥⎥⎤
混合比例为 w ∼ D i r i c h l e t ( α ) , α = ( 8 , 4 , 8 ) w\sim Dirichlet(\alpha)\ ,\ \alpha=(8,4,8) w∼Dirichlet(α) , α=(8,4,8)的GMM模型,在PyMC3中可以使用pm.Mixture或pm.DensityDist来构造似然函数并提取样本。
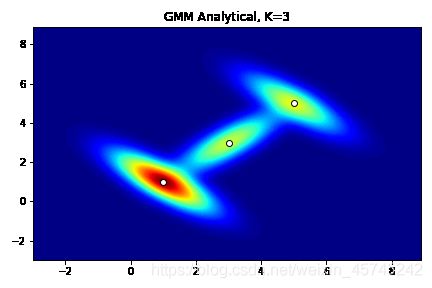
先构造解析数据,作为参照。
%matplotlib inline
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc3 as pm
import theano.tensor as tt
import seaborn as sns
from sklearn import mixture
import dill, theano
from scipy.stats import multivariate_normal as mvn
x,y = np.mgrid[-3:9:0.1, -3:9:0.1]
pos = np.dstack((x,y))
com1 = mvn(means[0],cov[0]).pdf(pos)
com2 = mvn(means[1],cov[1]).pdf(pos)
com3 = mvn(means[2],cov[2]).pdf(pos)
liklihood_function = w[0]*com1 + w[1]*com2 + w[2]*com3
fig = plt.figure(1)
ax = fig.add_subplot(111)
ax.contourf(x,y,liklihood_function,levels=100,cmap='jet')
ax.scatter(x=means[:,0], y=means[:,1], color='white', edgecolor='black')
plt.title('GMM Analytical, K=3')
plt.show()
构造似然函数的目标不在于估计,而是稳定产生较为准确的样本,所以应为模型提供尽可能多且准确的参数。
1.1 使用pm.Mixture
为减少PyMC3推理的负担,尽量将参数在模型外赋值。
K=3
means = np.array([1,1,3,3,5,5]).reshape((3,2))
cov = np.array([1, -0.8, -0.8, 1, 1, 0.8, 0.8, 1, 1, -0.8, -0.8, 1]).reshape((3,2,2))
alpha = np.array([8, 4, 8])
w = np.random.dirichlet(alpha)
with pm.Model() as model:
comp1 = pm.MvNormal.dist(mu=means[0], cov=cov[0], shape=2)
comp2 = pm.MvNormal.dist(mu=means[1], cov=cov[1], shape=2)
comp3 = pm.MvNormal.dist(mu=means[2], cov=cov[2], shape=2)
liklihood = pm.Mixture('liklihood', w=w, comp_dists=[comp1, comp2, comp3], shape=2)
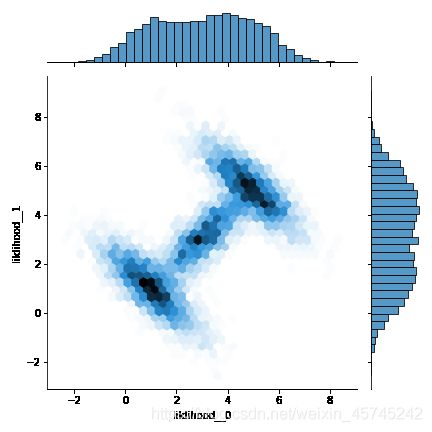
使用Slice采样并将轨迹转为DataFrame,使用seaborn.jointplot查看抽样结果:
with model:
trace = pm.sample(2000, step=pm.Slice(), tune=2000, pickle_backend='dill')
dftrace = pm.trace_to_dataframe(trace)
sns.jointplot(data=dftrace, x='liklihood__0', y='liklihood__1', kind='hex')
1.2 使用pm.DensityDist
使用theano构造解析函数后,指定对数似然函数,最后通过pm.DensityDist指定为似然函数。
#构造解析似然函数
cov_inverse = np.linalg.inv(cov)
z = tt.matrix('z')
z.tag.test_value=pm.floatX([0,0])
def gmm2dliklihood(z):
z = z.T
comp1 = 1/np.sqrt(2*np.pi*np.linalg.det(cov)[0])*np.exp(-1/2*(
(z[0]-means[0,0])**2*cov_inverse[0,0,0]
+(z[0]-means[0,0])*(z[1]-means[0,1])*cov_inverse[0,0,1]
+(z[1]-means[0,1])*(z[0]-means[0,0])*cov_inverse[0,1,0]
+(z[1]-means[0,1])**2*cov_inverse[0,1,1]))
comp2 = 1/np.sqrt(2*np.pi*np.linalg.det(cov)[1])*np.exp(-1/2*(
(z[0]-means[1,0])**2*cov_inverse[1,0,0]
+(z[0]-means[1,0])*(z[1]-means[1,1])*cov_inverse[1,0,1]
+(z[1]-means[1,1])*(z[0]-means[1,0])*cov_inverse[1,1,0]
+(z[1]-means[1,1])**2*cov_inverse[1,1,1]))
comp3 = 1/np.sqrt(2*np.pi*np.linalg.det(cov)[2])*np.exp(-1/2*(
(z[0]-means[2,0])**2*cov_inverse[2,0,0]
+(z[0]-means[2,0])*(z[1]-means[2,1])*cov_inverse[2,0,1]
+(z[1]-means[2,1])*(z[0]-means[2,0])*cov_inverse[2,1,0]
+(z[1]-means[2,1])**2*cov_inverse[2,1,1]))
return w[0]*comp1 + w[1]*comp2 + w[2]*comp3
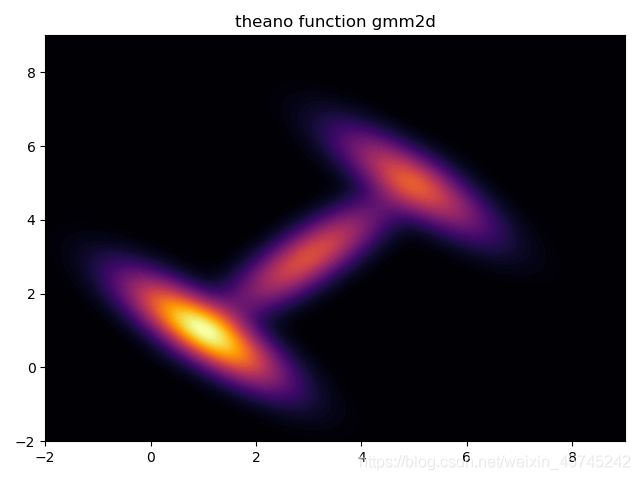
先确定构造的似然函数是否正确:
gmm2dliklihood_plot = theano.function([z],gmm2dliklihood(z))
grid = pm.floatX(np.mgrid[ -2:9:1000j, -2:9:1000j])
grid2d = grid.reshape(2, -1).T
pdf = gmm2dliklihood_plot(grid2d)
plt.contourf(grid[0], grid[1], pdf.reshape(1000, 1000), cmap='inferno',levels=80)
plt.title('theano function gmm2d')
plt.show()
from pymc3.distributions.dist_math import bound
#构造对数似然函数
def gmmlogp(z):
return np.log(gmm2dliklihood(z))
#将两种似然函数都传入模型,使用Slice采样并转为DataFrame
with pm.Model() as model:
gmm2dlike = pm.DensityDist("gmm2dlike", logp=gmmlogp, shape=(2,))
trace = pm.sample(2000, step=pm.Slice(), tune=2000, pickle_backend='dill')
dftrace = pm.trace_to_dataframe(trace)
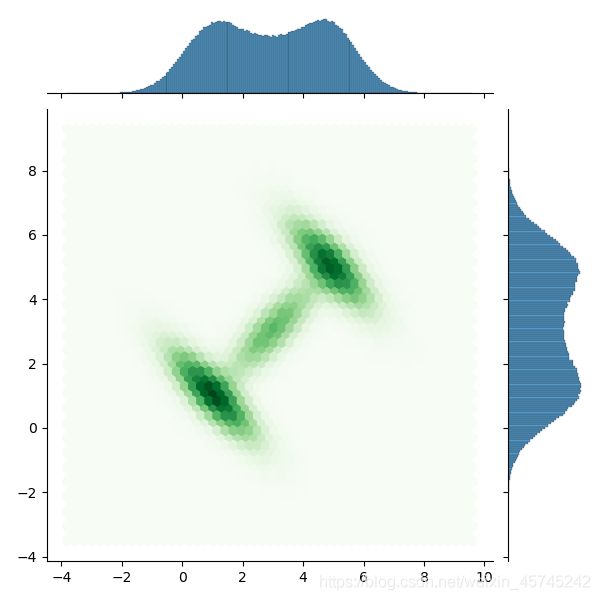
#通过jointplot查看
sns.jointplot(data=dftrace, x='gmm2dlike__0', y='gmm2dlike__1', kind='hex', cmap='Reds')
运行结果:
Multiprocess sampling (4 chains in 4 jobs)
Slice: [gmm2dlike]
100.00% [16000/16000 00:11<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 2_000 tune and 2_000 draw iterations (8_000 + 8_000 draws total) took 30 seconds.
The number of effective samples is smaller than 10% for some parameters.
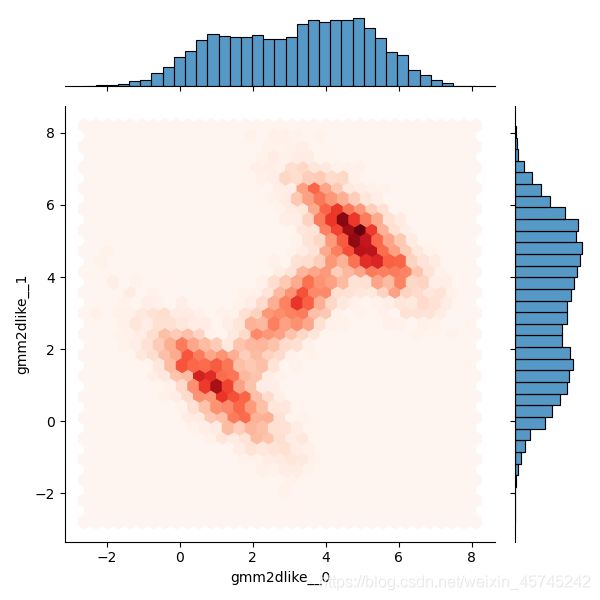
与解析数据及1.1中的结果基本一致,但通过这两种方式生成样本过慢,应考虑更快的方法。
2. 使用sklearn的GMM作为快速样本生成器
使用sklearn的gmm作为快速样本生成器,爱实践中会带来许多方便,比如我们需要100,000个甚至更多GMM似然函数样本点的时候,不需要通过PyMC3.sample进行漫长的MCMC采样,而是根据少量的MCMC样本,使用sklearn的gmm拟合,最后快速生成大量样本,从而节省时间。
from sklearn import mixture
skgmm = mixture.GaussianMixture(n_components=K
, covariance_type='full'
, weights_init=w
,means_init=means
)
skgmm.fit(trace['liklihood'])
sksamples, index = skgmm.sample(10000000)
sns.jointplot(x=sksamples[:,0], y=sksamples[:,1], kind='hex', cmap='Greens')
不妨计时来查看这二者之间的区别,依旧是同一个GMM似然函数,生成1,000,000个样本:
with pm.Model() as model:
comp1 = pm.MvNormal.dist(mu=means[0], cov=cov[0], shape=2)
comp2 = pm.MvNormal.dist(mu=means[1], cov=cov[1], shape=2)
comp3 = pm.MvNormal.dist(mu=means[2], cov=cov[2], shape=2)
liklihood = pm.Mixture('liklihood', w=w, comp_dists=[comp1, comp2, comp3], shape=2)
trace = pm.sample(1000000, step=pm.Slice(), tune=2000, pickle_backend='dill')
dftrace = pm.trace_to_dataframe(trace)
运行结果:
Multiprocess sampling (4 chains in 4 jobs)
Slice: [liklihood]
100.00% [4008000/4008000 47:17<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 2_000 tune and 1_000_000 draw iterations (8_000 + 4_000_000 draws total) took 2856 seconds.
The number of effective samples is smaller than 10% for some parameters.
或者是这种方式:
cov_inverse = np.linalg.inv(cov)
z = tt.matrix('z')
z.tag.test_value=pm.floatX([0,0])
def gmm2dliklihood(z):
z = z.T
comp1 = 1/np.sqrt(2*np.pi*np.linalg.det(cov)[0])*np.exp(-1/2*(
(z[0]-means[0,0])**2*cov_inverse[0,0,0]
+(z[0]-means[0,0])*(z[1]-means[0,1])*cov_inverse[0,0,1]
+(z[1]-means[0,1])*(z[0]-means[0,0])*cov_inverse[0,1,0]
+(z[1]-means[0,1])**2*cov_inverse[0,1,1]))
comp2 = 1/np.sqrt(2*np.pi*np.linalg.det(cov)[1])*np.exp(-1/2*(
(z[0]-means[1,0])**2*cov_inverse[1,0,0]
+(z[0]-means[1,0])*(z[1]-means[1,1])*cov_inverse[1,0,1]
+(z[1]-means[1,1])*(z[0]-means[1,0])*cov_inverse[1,1,0]
+(z[1]-means[1,1])**2*cov_inverse[1,1,1]))
comp3 = 1/np.sqrt(2*np.pi*np.linalg.det(cov)[2])*np.exp(-1/2*(
(z[0]-means[2,0])**2*cov_inverse[2,0,0]
+(z[0]-means[2,0])*(z[1]-means[2,1])*cov_inverse[2,0,1]
+(z[1]-means[2,1])*(z[0]-means[2,0])*cov_inverse[2,1,0]
+(z[1]-means[2,1])**2*cov_inverse[2,1,1]))
return w[0]*comp1 + w[1]*comp2 + w[2]*comp3
def gmmlogp(z):
return np.log(gmm2dliklihood(z))
with pm.Model() as model:
gmm2dlike = pm.DensityDist("gmm2dlike", logp=gmmlogp, shape=(2,))
trace = pm.sample(1000000, step=pm.Slice(), tune=2000, pickle_backend='dill')
dftrace = pm.trace_to_dataframe(trace)
运行结果:
Multiprocess sampling (4 chains in 4 jobs)
Slice: [gmm2dlike]
100.00% [4008000/4008000 24:18<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 2_000 tune and 1_000_000 draw iterations (8_000 + 4_000_000 draws total) took 1475 seconds.
The number of effective samples is smaller than 10% for some parameters.
需要的时间都很长,而使用少量样本+sklearnGMM的方式:
from pymc3.distributions.dist_math import bound
from sklearn import mixture
def gmmlogp(z):
return np.log(gmm2dliklihood(z))
with pm.Model() as model:
gmm2dlike = pm.DensityDist("gmm2dlike", logp=gmmlogp, shape=(2,))
trace = pm.sample(400, step=pm.Slice(), pickle_backend='dill')
dftrace = pm.trace_to_dataframe(trace)
Only 400 samples in chain.
Multiprocess sampling (4 chains in 4 jobs)
Slice: [gmm2dlike]
100.00% [5600/5600 00:06<00:00 Sampling 4 chains, 0 divergences]
Sampling 4 chains for 1_000 tune and 400 draw iterations (4_000 + 1_600 draws total) took 23 seconds.
The rhat statistic is larger than 1.05 for some parameters. This indicates slight problems during sampling.
The estimated number of effective samples is smaller than 200 for some parameters.
%%time
skgmm = mixture.GaussianMixture(n_components=K
, covariance_type='full'
, weights_init=w
,means_init=means)
skgmm.fit(trace['gmm2dlike'])
sksamples, index = skgmm.sample(1000000)
sns.jointplot(data=dftrace, x='gmm2dlike__0', y='gmm2dlike__1', kind='hex', cmap='Reds')
Wall time: 173 ms
运行结果: