决策树-ID3

决策树的ID3算法

基本概念

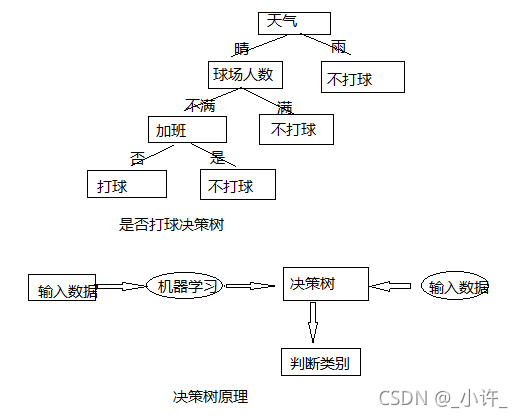
• 决策树是一个树状结构，它包含一个根节点，若干内部节点和若干叶子节点。根节点包含样本全集，叶子节点对应决策结果，内部节点对应一个特征和属性或属性测试。从根节点到每个叶子节点的路径对应了一个判定测试序列，决策树学习的目的是为了产生一颗泛化能力强，即处理未见示例能力强的决策树，器基本流程遵循简单而直观的分而治之策略，决策树的生成是一个递归过程。
• 构造决策树的核心问题在于每一步如何选择适当的特征对样本做拆分，其主要算法有CART, ID3, C4.5 ； CART使用Gini指数作为选择特征 的准 则。ID3 使用信息增益 作 为选择特征的 准 则 。C4.5使用信息增益比作为选择特征的准则。决策树的剪枝是为了防止树的过拟合，增强其泛化能力，包括预剪枝和后剪枝。
• 决策树的优缺点

1. 决策树算法易于理解，能做可视化分析，容易提取出规则。其次，决策树可同时处理标称型和数值型数据。在
   次，决策树能很好的扩展到大型数据库中。

2. 决策树容易因样本太少而特征太多出现过拟合，忽略了数据集中属性的相关联，ID3算法计算信息增益是结果偏向数值比较多的特征。

信息熵

数学期望：每次可能的结果的概率乘以其结果的的总和。
信息价值：在沙漠地区，告诉你明天不下雨，和明天下雨的信息价值是不同的，前者为高概率，显然概率越小的事件其价值越高。信息价值公式：$$l(xi)=-lo{g}_{2}p(xi)$$

// 信息值与概率的关系
from math import log
import matplotlib.pyplot as plt
x= [i/100 for i in range(1,100)]
p=[-log(i,2) for i in x]
plt.xlabel("x")
plt.ylabel("l(x)")
plt.plot(x,p)
plt.show()

决策树原理（以是否打球决策树为例）：

简化程序，ID3算法处理的是数值型数据，先将文字转化数值会方便很多。这里的0，1，2分别表示三个特征，天气，球场人数，加班；4表示类别；表中的0，1表示该特征状态下的“No”和“Yes”。

在构造决策树树时，需要将那些起决定性作用的特征作为首要决策点，须利用一定算法对特征进行评估也是上面的三个算法。 

信息熵：一条信息的信息量大小和和它的不确定性有直接关系，信息熵是信息价值的数学期望【即类别的信息价值平均值】。公式：$$H=-\sum _{n=0}^{n}p(xi)lo{g}_{2}p(xi)$$

# 导入包
import numpy as np
import pandas as pd

#导入数据
data={
    0:[1,0,0,"打球"],
    1:[1,0,1,"打球"],
    2:[0,1,1,"打球"],
    3:[0,0,1,"不打球"],
    4:[1,1,1,"打球"]
}

# 计算熵的函数
def ent(data):
    print("原始数据：")
    df0=pd.DataFrame(data)
    print(df0)
    print("整理后的数据")
    df=df0.T
    print(df)
    print("数据长度：")
    data_length=len(data)
    print(data_length)
    print("取出结论熵【信息价值的期望值】")
    target=df.iloc[:,-1]  # pandas的行列操作函数loc和iloc
    print(target)
    print("分类计数")
    label_counts=target.value_counts()  # pandas的value_counts()计数函数
    print(label_counts)
    print("转字典类型")
    label_dict=label_counts.to_dict()    #pandas的转换字典的函数
    print(label_dict)
    entropy=0
    for key in label_dict:
        prob=float(label_dict[key])/data_length
        entropy-=prob*np.log2(prob)
    return entropy
print(ent(data))

最后输出的0.7219280948873623就是类别信息熵。

信息增益：类别信息熵与某个属性状态下不同特征的信息熵【条件概率】的差值，公式：$$info（H）=H-\sum _{i=1}^v\frac{Hv}{H}\chi H(v)$$

公式含义是：不同属性下，各个特征与总数据量的比例乘该特征下的信息熵的总和。（有点难理解，接下来会用数学表达式进一步解释）

#导入库
import pandas as pd
import numpy as np
#写入数据
data={
    0:[1,1,0,0,1],
    1:[0,0,1,0,1],
    2:[0,1,1,1,1],
    3:["打球","打球","打球","不打球","打球"]
}
#pandas处理数据
df=pd.DataFrame(data)
print(df)

#封装计算熵的函数
def ent(df):
    target=df.iloc[:,-1] #取表的最后一列仍为DataFrame类型
    data_length=len(df)
    label_counts=target.value_counts() #value_count()聚合函数，统计数量
    label_dict=label_counts.to_dict() #将统计后的结果转化为字典类型
    entropy=0 #初始化熵的值
    #熵的计算公式
    for key in label_dict:
        prob=float(label_dict[key])/data_length
        entropy-=prob*np.log2(prob)
    return entropy

#封装分割数据的函数
def split(df,feature_rank):
    groups=df.groupby(feature_rank)
    data_group={}
    for key in groups.groups.keys():
        data_group[key]=df.loc[groups.groups[key],:]
    return data_group

def _main_(data,feature_rank):
    init=ent(data)
    group_dict=split(data,feature_rank)
    new_ent=0
    for key in group_dict:
        prob=len(group_dict[key])/len(data)
        new_ent+=prob*ent(group_dict[key])
    return init-new_ent
print(_main_(data,0))
    

资料数值算法思想均来源于Python机器学习开发实战（王新宇编著，人名邮电出版版社，谢谢！！！）

// 分别计算0，1，2特征的信息增益
print("特征0的信息增益为：",_main_(data,0))
print("特征1的信息增益为：",_main_(data,1))
print("特征2的信息增益为：",_main_(data,2))

特征	信息增益
0（天气）	0.3219
1 （球场人数）	0.1709
2 （加班）	0.0729

计算的出的信息增益可以看出，天气对是否打球影响对大，加班最小，通过排序可以依次列出特征对结果的影响的分布，并以此选择特征构造决策树。

信息增益详述： （以下表中的数据为例）

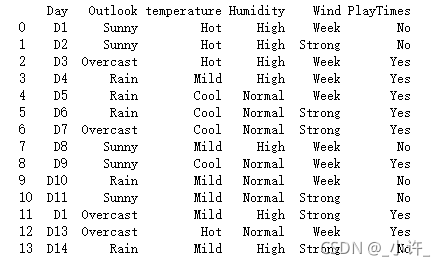
该表是两周内是否有PlayTimes的数据，对于Outlook的属性来说，其一共有三种特征即Sunnny,Rain,Overcast
对于类别统计：

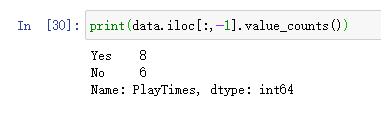
那么对于整个表来说其类别信息熵为：$$H(PlayTimes)=-\frac{9}{14}lo{g}_2\frac{9}{14}-\frac{5}{14}lo{g}_2\frac{5}{14}=0.942107$$

属性Outlook的熵（三个熵值）：

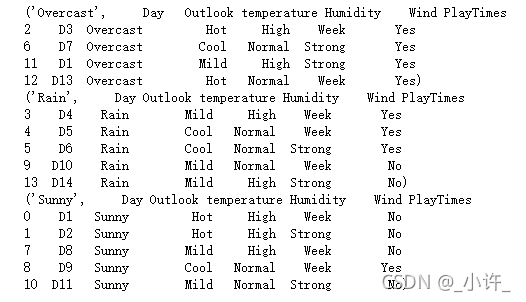
Rain特征总数为5，其中Yes占3/5，No占2/5；Sunny特征总数为5，Yes占2/5，No占3/5；Overcast特征总数为4，Yes占100%

$$Overcast的信息熵：H(Overcast)=-\frac{4}{4}lo{g}_2\frac{4}{4}-0=1.0$$
$$Sunny的信息熵：H(Sunny)=-\frac{2}{5}lo{g}_2\frac{2}{5}-\frac{3}{5}lo{g}_2\frac{3}{5}=0.970$$
$$Rain的信息熵：H(Rain)=-\frac{4}{5}lo{g}_2\frac{4}{5}-\frac{1}{5}lo{g}_2\frac{1}{5}=0.722$$
$$Overlook的信息增益：G(Rain)=H(PlayTimes)-(\frac{4}{14}H(Overcast)+\frac{5}{14}H(Sunny)+\frac{5}{14}H(Rain)=0.888$$
到此已经计算出Overlook的信息增益了。

构造决策树

计算信息增益就是为了在当前状态下选择最合适特征作为节点，以递归构造决策树，而构造决策树的目的反过来又是对新的数据分类，确定未知的数据类别。具体就是需要一部分数据作为训练集指定规则（决策树），然后利用这些规则（决策树）对新的数据进行分类。

具体构造决策树的流程参照生成决策树@代码拖拉鸡，谢谢！！！

那么，如何用代码实现呢？DecisionTreeClassifier方法已经集成了生成决策树的代码，我们只需要会运用即可。

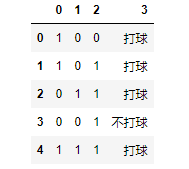
上表中的数据构建决策树，并判断[1,1,0]是否打球？

#以是否打球为例构建决策树

import pandas as pd
data={
    0:[1,0,0,"打球"],
    1:[1,0,1,"打球"],
    2:[0,1,1,"打球"],
    3:[0,0,1,"不打球"],
    4:[1,1,1,"打球"]
}
df0=pd.DataFrame(data)
df=df0.T
print(df)

from sklearn import tree  #导入模块
x=[[1,0,0],[1,0,1],[0,1,1],[0,0,1],[1,1,1]]   #训练集的数据，矩阵类型(0，1分别表示不同特征)
y=[1,1,1,0,1]    #训练集类别  列表类型（0，1表示不同类别）
tree_model = tree.DecisionTreeClassifier(criterion='entropy')  #构造决策树模型，entropy表示信息增益计算即ID3算法
clf = tree_model.fit(x, y)   #用构建的决策树模型拟合训练数据
clf.predict([[1,1,0]])   #预测[1,1,0]是否打球

结果：

输出了1，表示打球，即[1,1,0]状态下也打球。
构建的决策树如下：

// 输出决策树代码
# 可以用 Graphviz 格式（export_graphviz）输出。
# 如果使用的是 conda 包管理器，可以用如下方式安装：
# conda install python-graphviz  window+r +cmd中进行
# pip install graphviz


# 以下展示了用 Graphviz 输出上述从鸢尾花数据集得到的决策树，结果保存为 iris.pdf

# import graphviz
# iris = load_iris()
# dot_data = tree.export_graphviz(clf, out_file=None)
# graph = graphviz.Source(dot_data)
# graph.render("iris")
# export_graphviz 支持使用参数进行视觉优化，包括根据分类或者回归值绘制彩色的结点，也可以使用显式的变量或者类名。
# Jupyter Notebook 还可以自动内联呈现这些绘图。


import graphviz     
#iris = load_iris()
clf = tree.export_graphviz(tree_model, out_file=None)
graph = graphviz.Source(clf)
graph

后续会更新c4.5算法