35、算法的概述和解析算法、枚举算法

前面我们已经将Python语法部分的知识都讲完了。前面我们拿到一个程序题，我们都是按照自己的思路直接写代码，但是复杂的程序就不是那么容易直接写出来的了，需要分析整体的思路。从这节课开始我们要讲算法的相关知识了。算法是对解题方法的精确而完整的描述，即解决问题的方法和步骤。算法不受语言的限制，不论是使用Python还是使用其他语言，算法都是一样的，算法分析出来以后，可以很轻松的得到程序的代码。我们正式开始这节课的内容吧。

一、使用计算机解决问题的过程

我们要使用计算机解决问题，一般分为三个阶段：

1. 分析问题，建立模型
2. 设计算法
3. 实现算法和检验结果

解决问题前，我们要对问题进行分析和描述，根据分析的情况构建数学模型。然后再确定让计算机怎样做。最后用计算机运行设计好的程序解决问题，并对结果进行检测、分析和验证。算法就是“确定让计算机怎样做”这一步。

计算机的程序主要有以下两个部分组成：

1. 指令部分：每条指令指定计算机执行的一个操作，由一系列指令构成的序列，描述了解决问题的计算过程。
2. 数据部分：计算时需要对原始数据，计算的中间结果和最后结果。

根据计算机程序的这两个部分，我们在设计程序时，也需要考虑两方面的问题：

1. 数据的存储：计算所需要对原始数据，需要存储在不同的变量中。
2. 计算的过程：确定解决问题的方法，把方法步骤化，再用计算机能执行的指令实现相应的步骤。

二、算法的特点和表示方法

算法是解决问题的方法和步骤，那就必须是计算机能够执行的，并且数据能够被人看到的，总结下来有以下几个特点：

1. 有穷性：执行的步骤是有限的
2. 确定性：每个步骤的含义必须是明确的
3. 可行性：每个步骤是可行的，并且能够在有限的时间内完成
4. 有0个或多个输入：初始数据可以从外界输入，有可以含在算法中
5. 有一个或多个输出：算法一定要有结果并且以一定方式输出

算法是与计算机语言无关的，那我们就需要使用一定的方法将算法表示出来。算法的表示方法主要分为三种方式：自然语言、流程图、伪代码。其中自然语言和流程图我们需要现阶段需要掌握，伪代码是流程图的一种代码简化形式，有兴趣的同学可以课后自己研究。

2.1 自然语言

自然语言是指人们日常生活中使用的语言，用自然语言描述的算法通俗易懂，但是缺乏直观性和简洁性，也容易产生歧义。

我们看一下自然语言表示算法的方式。假设我们要计算一个球的体积，使用自然语言描述如下：

1. 输入球的半径r
2. 计算球的体积V（）
3. 输出结果V
4. 结束

通过以上的自然语言，我们很容易就可以转换成Python的代码：

from math import pi

r = float(input())
v = 4 / 3 * pi * r ** 3
print(v)

这种描述方式与我们平时日常交流的语言没有任何区别，也很容易理解。但是如果需要解决的问题比较复杂，就显得表述很冗长。

2.2 流程图

流程图也称程序框图，它是算法的一种图形化的表示方法，与自然语言相比，它描述的算法形象、直观，更容易理解。在学习流程图之前，我们需要先认识一下流程图中的各种常用符号的含义：

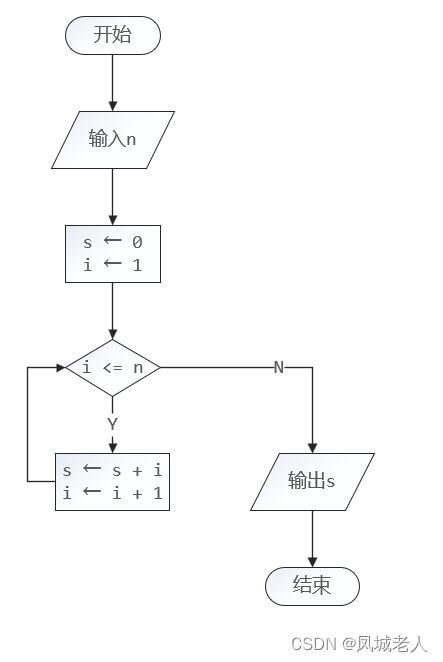
 下面我们使用流程图描述一下1+2+3+...+n的算法表示：

三、解析算法

解析算法是算法中最为简单、最为基本的一种，解析的定义是：用数学公式描述客观事物间的数量关系。解析算法即用解析的方法找出表示问题的前提条件和结果之间关系的数学表达式，并通过表达式计算来实现问题的求解。

解析算法的实现有以下步骤：

1. 建立正确的数学模型
2. 将数学表达式转换为Python表达式

比如以下问题可以使用解析算法求解：

出租车的计价规则为：3千米以内起步价为10元；超出3千米，每千米单价为2元。如果里程数为x，收费金额为y。我们可以得到以下公式：

通过公式我们可以很容易写出程序的代码：

x = int(input())
if x <= 3:
    y = 10
else:
    y = 10 + 2 * (x - 3)
print(y)

在使用解析算法时我们要注意以下问题：

1. 数学表达式转换为Python时，可能会把运算符、运算顺序写错
2. 要留意分支结构的解析算法

四、枚举算法

枚举算法也叫穷举算法，它的基本思想是把问题所有的解一一罗列出来，并对每一个可能解进行判断，以确定这个可能解是否是问题的真正解。如果是就采用，不是就抛弃。

枚举算法的要点：

1. 列举的可能性即不重复也不遗漏
2. 尽可能缩小罗列的范围，以提高效率
3. 用循环语句在列举的范围内列举所有可能的解
4. 用判断语句选择真正的解

我们举个例子来看一下什么样的问题适合用枚举算法：

有一盒乒乓球，9个9个的数，最后余下7个；5个5个的数，最后余下2个；4个4个的数，最后余下1个。这盒乒乓球至少有多少个？

我们根据思路，从最小的数开始一个一个的试，直到得到我们想要的结果。那最小的数字是多少呢？我们先要缩小罗列的范围。9个9个数余7，9 + 7 = 16；5个5个数余2，5 + 2 = 7；4个4个数余1，4 + 1 = 5。我们可以看出，最小从16开始枚举最合适。

 根据算法我们可以很容易写出代码：

n = 16
while True:
    if n % 9 == 7 and n % 5 == 2 and n % 4 == 1:
        print(n)
        break
    n += 1

五、课后思考题

1、选择题

下列问题适合用解析算法求解的是（）

A. 将13张纸牌按从小到大的顺序进行排列

B. 统计100以内各位数字之和恰好为10的偶数的个数

C. 计算一辆车行驶100千米的油耗

D. 寻找全年级身高最高的同学

 2、选择题

用50元钱兑换面值1元、5元、10元的纸币，为有多少种兑换方案。求解这个问题，最适合的算法是（）

A. 排序算法        B. 递归算法        C. 枚举算法        D. 解析算法

3、编程题

寻找100~999的所有水仙花数，并统计个数。

水仙花数是指各位数字的立方和等于该数本身的三位数。例如：。

六、上节课思考题答案

1、A

2、参考代码：

import datetime

today = datetime.datetime(2022, 12, 2)
a = datetime.timedelta(142)
birthday = today + a
print(birthday.month, '月', birthday.day, '日', sep='')