动态规划（01背包和完全背包系列）

1. 背包问题总结模板

这两道题分别是动态规划中背包问题的一种，我们可以大致把背包问题分为01背包和完全背包以及组合背包问题。
1.

• 01背包问题就是：从n个物品中选取当容积达到m的时候，背包此时的价值最大。但是背包中每种物品只能选取一次
• 完全背包则是：此时从n个物品中选取当容积达到m的时候，背包的此时价值最大，但是每种物品都可以重复选取
• 组合背包（组合和排列）问题：此时我们需要对背包中的物品要考虑顺序（然而这一种才是最应该好好思考的，因为他的遍历顺序是有严格的方式的，如果我们选择了不恰当的遍历方式，这里是会报错的，对于排序问题我们应该选择先遍历容积在遍历物品，对于组合问题我们依旧选择和别的方式一样的先遍历物品在遍历，为什么要这样呢？那是因为如果我们在排序哪里依旧使用原来的遍历顺序，是会出现重复的结果的，比如说{1，5}和{5，1},在组合里面这两个结果算一个，但是在排序里面这算两个结果）

2.首先是背包分类的模板：

• 1、0/1背包：外循环nums,内循环target,target倒序且target>=nums[i];
• 2、完全背包：外循环nums,内循环target,target正序且target>=nums[i];
• 3、组合背包(考虑顺序)：外循环target,内循环nums,target正序且target>=nums[i];
• 4、分组背包：这个比较特殊，需要三重循环：外循环背包bags,内部两层循环根据题目的要求转化为1,2,3三种背包类型的模板（待定）

3.问题分类的模板：

• 1、最值问题: dp[i] = max/min(dp[i], dp[i-nums]+1)或dp[i] = max/min(dp[i], dp[i-num]+nums);
• 2、存在问题(bool)：dp[i]=dp[i]||dp[i-num]；
• 3、组合问题：dp[i]+=dp[i-num];

2. 01背包系列题目

2.1 LintCode—01背包问题

链接：https://www.lintcode.com/problem/125/

题解：

仔细感觉就会发现其实是在填这个物品和容积所构成的一个表格（一定要对于物品和容量所开辟的表格多开一行一列，这样做的目的也是为了能够直接进行初始化），最终需要返回的是dp[n][m],也就是从前n个物品当中任意选择物品，且体积总和不超过m的最大价值。

class Solution{
public:
 int backPackII(int m, vector<int> &A, vector<int> &V) {
        // write your code here
        int n = A.size();
        vector<vector<int>> dp(n+1,vector<int>(m+1,0));
        for(int i = 1;i<=n;++i)
        {
            for(int j = 1;j<=m;++j)
            {
                if(A[i-1] > j)
                {
                    //肯定是放不下的
                    dp[i][j] = dp[i-1][j];
                }
                else
                {
                    dp[i][j] = std::max(dp[i-1][j-A[i-1]]+V[i-1],dp[i-1][j]);
                }
            }
        }
        return dp[n][m];
    }
};

2.2 LeetCode第416题—分割等和子集(存在问题)

这道题和sum和一样，如何找到这道题是一道01背包问题，是这道题的关键。

class Solution {
public:
    //left - right = 0;
    //left + right = sum;
    //2left = sum           ->      left = sum/2
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        for(int& e: nums)
            sum += e;
        if(sum % 2 == 1)
            return false;
        int bigSize = sum /2;
        vector<vector<int>> dp(nums.size()+1,vector<int>(bigSize+1,false));
        dp[0][0] = true;
        for(int i = 1;i<=nums.size();++i)
        {
            for(int j = 1;j<=bigSize;++j)
            {
                if(j < nums[i-1])
                    dp[i][j] = dp[i-1][j];
                else
                    dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i-1]];
            }
        }
        return dp[nums.size()][bigSize];
    }
};

2.3 LeetCode第494题—目标和（重点，还需要继续好好思考）

target可能题目已经给出(显式)，也可能是需要我们从题目的信息中挖掘出来(非显式)(常见的非显式target比如sum/2等)

class Solution {
public:
    //这道题就是典型的隐式target，那么如何得到这个target呢？
    //怎么看出来他是01背包问题呢？
    //left - right = target
    //数组和sum(固定的)
    //left -(sum-left) = target
    //left = (target+sum) / 2
    //此时我们就得到了，那么背包的容量
    //dp[i]表示当容量为i的时候，能装满有几种方式
    int findTargetSumWays(vector<int>& nums, int target) {
        int sum = 0;
        for(int& e: nums)
            sum += e;
        if(abs(target) > sum)
            return 0;
        //此时我们可以假设sum 是5，target是2，那么此时就是无解
        if((sum + target) % 2 == 1)
            return 0;
        int bigsize = (sum + target) / 2;//背包的容积
        vector<int> dp(bigsize+1,0);
        dp[0] = 1;
        for(int i = 0;i<nums.size();++i)
        {
            //对于01背包写为一维的一定在内循环要写成倒叙，因为只有这样才能够保证每个物品不被重复选择
            for(int j = bigsize;j >= nums[i];j--)
            {
                    dp[j] += dp[j -nums[i]];
            }
        }
        return dp[bigsize];
    }
};

3. 完全背包系列题目

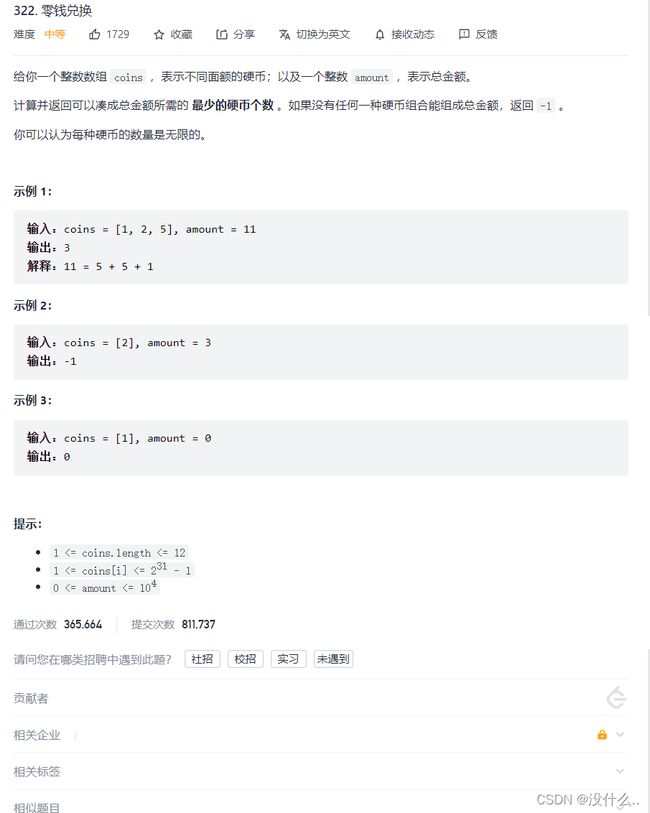
3.1 LeetCode第322题—零钱兑换I(最大最小值问题)

• 其实和青蛙跳台阶这道题是有异曲同工之妙的，dp[6] =min {dp[5],dp[4],dp[1]}（假设我们举得例子就是一次可以跳1步、2步和5步，跳到第6步我们此时可以选择最后一步分别是跳1步、2步和5步中选取跳的次数最少的哪一种，不断的更新我们所需要的dp数组）
• 但是这里还有一个疑问就是，我们应该i怎样考虑两层for循环的遍历问题。正常来说我们应该首先选择物品在选择背包的容积来遍历，这样子是最好的，就记住这个框架就不会有啥大问题。

class Solution {
public:
    //好像有那么一点点味道了，我们可以把这道题抽象成变态青蛙跳台阶的问题，我可以选择一次走1步，2步或者5步
    //现在我要求得，走到第11步的时候跳跃步骤最少的方法
    //最少的硬币个数
    //dp[i]表示当金额为i时所需要的最小硬币个数
    //这个dp数组存放的是从0一直到amount过程中到达每一个位置所需要的最小步数
        int coinChange(vector<int>& coins, int amount) {
        int Max = amount + 1;
        vector<int> dp(amount + 1, Max);
        dp[0] = 0;
        for (int i = 1; i <= amount; ++i) {
            for (int j = 0; j < coins.size(); ++j) {
                if (coins[j] <= i) {
                    dp[i] = min(dp[i], dp[i - coins[j]] + 1);
                }
            }
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }
};

3.2 LeetCode第518题—零钱兑换II（组合问题）

这道题的顺序才是更准确的，我们应该首先遍历物品，在遍历容积

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        vector<int> dp(amount+1,0);
        dp[0] = 1;
        //对于组合数是需要考虑到去重问题的，如果是这样进行循环那么就有可能会出现顺序不同，但是组合相同的结果
        //总结一下就是先遍历物品在遍历金额会更好一些
        for(int i = 0;i<coins.size();++i)
        {
            for(int j = 1;j<=amount;++j)
            {
                if(coins[i] <= j)
                    dp[j] += dp[j-coins[i]];
            }
        }
        return dp[amount];
    }
};

3.3 LeetCode第377题—组合总和IV（排列问题）

• 这道题我们就需要严格的控制好遍历的顺序，先遍历容积，在遍历物品，这样我们就可以得到全部的排列。
• 但是这道题还有一点就很恶心，为什么？因为会出现大数溢出的情况，所以判断条件必须增加。
• 其实题目当中已经给出了提示，那就是保证整数符合32位的整数范围，在每次叠加 的时候，都有可能会超过INT_MAX，所以这里需要进行一下判断。

class Solution {
public:
    //组合数和排列数是不一样的
    //你仔细感觉这道题是不是和零钱兑换的题目很像
    //根据测试用例可以知道，这道题是一个求排列数的题目
    int combinationSum4(vector<int>& nums, int target) {
        vector<int> dp(target+1,0);
        //这里是不是还应该考虑一下dp的初始条件的情况
        //因为你的递归这里的时候，dp[1] += dp[0] ,如果此时dp[0]初始化是0，那么dp[1]的组合数也是0，是错误的
        dp[0] = 1;
        for(int i = 1;i<=target;++i)
        {
            for(int j = 0;j<nums.size();++j)
            {
                //其实题目也给出了一个隐蔽的条件：保证答案符合32为整数范围
                if(nums[j] <= i && dp[i-nums[j]] < INT_MAX -dp[i])
                    dp[i] += dp[i-nums[j]];
            }
        }
        return dp[target];
    }
};

3.4 LeetCode第279题—完全平方数（和零钱兑换I基本一致）

LeetCode题目链接:https://leetcode-cn.com/problems/perfect-squares/

记住了：只要是求最小值初始化的时候就应该使用INT_MAX，因为如果初始化为0的话，可能会造成覆盖，出现错误

class Solution {
public:
    int numSquares(int n) {
        //和为n的完全平方数的最少数量，看到了这个最小数量就应该要想到是否这道题是完全
        //对于这道题我们需要分析的就是何为物品何为容积
        //根据测试用例也可以知道，每一个数都是可以被重复选择的
        //这道题给我们提供了一种方式就是如何，来取得1，4，9这些数的方法
        vector<int> dp(n+1,INT_MAX);
        dp[0] = 0;
        for(int i = 1;i<=n;++i) //可以看成容量
        {
            for(int j = 1;j*j <=i;++j) //可以看成物品
            {
                dp[i] = min(dp[i],dp[i-j*j]+1);
            }
        }
        return dp[n];
    }
};

3.5 LeetCode第139题—单词拆分（存在问题)

LeetCode题目链接:https://leetcode-cn.com/problems/word-break/

题解：单词就是物品，字符串s就是背包，单词能否组成字符串s，就是问物品能不能把背包装满。

• 状态的定义dp[i] : 字符串长度为i的话，dp[i]为true，表示可以拆分为一个或多个在字典中出现的单词。
• 接下来就是如何来想状态方程转移的问题了？这里如何来表示这个物品呢？
• 递推公式是： if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true（前八位能否拆分取决于前五位能否拆分，加上五到八位是否属于字典（这句话才是整个这道题能够理解通的关键所在））
• dp[8]表示，dp[4]能否切割以及4-8的字符串出现在字典中

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        //能否使用字典里面给出来的字符串拼接出来我们想要的字符串s
        //但我还是没想出来为什么这道题可以使用动态规划的思想来做
        //dp[i]表示，当字符串长度为i的时候，能够切割出来1个或者多个单词在字典中找到
        unordered_set<string> us(wordDict.begin(),wordDict.end());
        vector<bool> dp(s.size()+1,false);
        dp[0] = true; //你会发现这个是整个递归的七点，如果他是false，那么后面的许多结果都是不正确的
        for(int i = 1;i<=s.size();++i)
        {
            for(int j = 0;j<i;++j)
            {
                //这里是要得到当字符串长度为i的时候，所有字串的可能
                //前八位能否拆分取决于前五位能否拆分，加上五到八位是否属于字典
                //这里你也就知道为什么解题答案要这么写了
                string str = s.substr(j,i-j);//(起始位置，截取的个数)
                if(us.find(str) != us.end() && dp[j])
                    dp[i] = true;
            }
        }
        return dp[s.size()];
    }
};

3.6 LeetCode第70题—爬楼梯

LeetCode题目链接:https://leetcode-cn.com/problems/climbing-stairs/
我很好奇为什么我第一次想这道题的想法却通过不了，他到底和我原来做的爬楼梯的方法有啥不同？真的蠢，那是在初始条件上有不同呀

①正常的动态规划思想

class Solution {
public:
    //思考问题要全面呢，如果n<=2 这两种情况也要考虑到
    int climbStairs(int n) {
        if(n <= 2)
            return n;
        vector<int> dp(n+1,0);
        dp[1] = 1;
        dp[2] = 2;
        for(int i = 3;i<=n;++i)
        {
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
};

②空间复杂度更低一些

class Solution {
public:
    int climbStairs(int n) {
        //这道题就是很好的一道动态规划的斐波那契额数列的题
        //f(n) = f(n-1)+f(n-2)
        //这道题和真正的原来做过的爬台阶好像是由那么一点不一样的
        //因为初始化的条件不一样
        //这样做的最好方法就是优化了空间复杂度
        if(n <= 2)
            return n;
        int f1 = 1;
        int f2 = 2;
        int ret = 0;
        for(int i = 3;i<=n;++i)
        {
            ret = f1 + f2;
            f1 = f2;
            f2 = ret;
        }
        return ret;
    }
};

参考Blog：

• 详解背包问题动态规划链接: ： https://leetcode-cn.com/problems/coin-change/solution/yi-pian-wen-zhang-chi-tou-bei-bao-wen-ti-sq9n/