01背包与完全背包详解

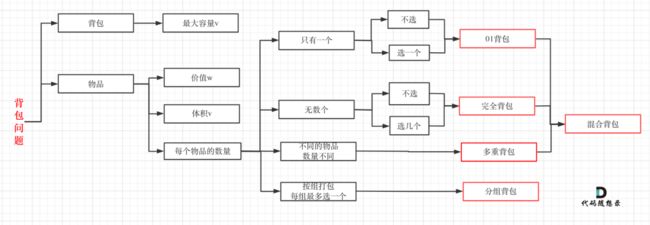
背包问题

只需要知道0-1背包和完全背包问题就完全足够了

0-1背包有以下的特点

• 有限个物体(有重量和价值)，每个物体只有一个
• 每个物体你都可以任选，可选也可以不选
• 有限制（上限或者下限）而且这个限制不能太

dp定义

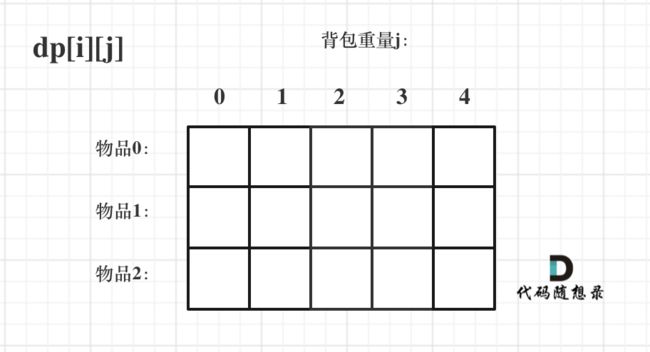
对于背包问题，有一种写法， 是使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

关于背包的两个关键点

• 第一怎么01背包降维的时候要反序遍历
• 第二为什么完全背包问题的时候组合的时候先遍历物品，后遍历背包容量

01背包

接下来来详细解答这两个关键：

以下面的例子为例

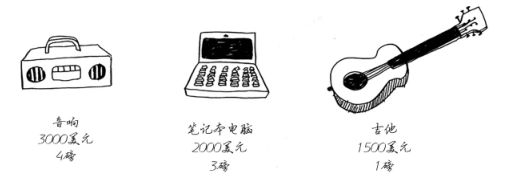
假设你是一个小偷，背着一个可装下4磅东西的背包，你可以偷窃的物品如下：

为了让偷窃的商品价值最高，你该选择哪些商品？

这就是典型的背包问题
物品也就是nums
背包容量也就是 target

第一种解法： 定义二维dp数组
dp[i][j]: 表示在前i个物品中能放进j容量能有多少种方法
也就是说每一物体只有两种选择为正数或者负数

对于01背包问题先遍历物品和先遍历背包都是一样的只是先遍历物品更好理解

二维

先遍历物品

// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
    for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量 
        if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 这个是为了展现dp数组里元素的变化
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
        
    }
}

先遍历背包

// weight数组的大小 就是物品个数
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
    for(int i = 1; i < weight.size(); i++) { // 遍历物品
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    }
}

一维(倒着遍历防止被重复放入，详解看图)

  for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }

参考链接

完全背包

完全背包的特点就是物品有无限个想怎么拿就怎么拿，所以对于纯完全背包问题先遍历背包和先遍历物品是一样的，但是如果变化那么区别就在于我们的遍历顺序

什么是完全背包问题

有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

注意这里说的是，求解放入背包的物品价值总和最大，也就是说你这物品的放入是有序还是无序我都可以的，不管你怎么放入，这个是完全背包的一个关键点

所以在这里纯完全背包问题就是可以先遍历物品或者先遍历背包都是可以的。

279. 完全平方数

难度中等880

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

给你一个整数 n ，返回和为 n 的完全平方数的 最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4

示例 2：

输入：n = 13
输出：2
解释：13 = 4 + 9

先遍历物品后遍历背包

class Solution {
public:
    int numSquares(int n) {
        // 首先这就是这个纯完全背包问题，也就是说物体是小于n的所有完全平方数，
        // 背包就是n，至于物品是否的有序或者无序放入就无所谓了，你随便放

        // 所以先遍历背包还是先遍历物品都是可以的

        /* 
            这里先遍历物品
         */

         // 先求符合条件的完全平方数
         vector data;
         for(int i=1;i<=n;i++) {
             if(i*i<=n) {
                 data.push_back(i*i);
             } else {
                 break;
             }
         }


         // 定义dp
         vector dp(n+1,0);
        // 初始化
        for(int i=1;i<=n;i++) {
            if(i%data[0]==0) {
                dp[i]=i/data[0];
            }
        }

         for(int i=1;i

解法2

public:
    int numSquares(int n) {
        vector dp(n + 1, INT_MAX);
        dp[0] = 0;
        for (int i = 0; i <= n; i++) { // 遍历背包
            for (int j = 1; j * j <= i; j++) { // 遍历物品
                dp[i] = min(dp[i - j * j] + 1, dp[i]);
            }
        }
        return dp[n];
    }
};

这里dp[0]=0的含义就和上面的不一样，，这里dp[0]代表的是没有物品的时候，各个容量所能放的最大价值，其实也是通过二维状态压缩过来的

先遍历背包后遍历物体

class Solution {
public:
    int numSquares(int n) {
        // 首先这就是这个纯完全背包问题，也就是说物体是小于n的所有完全平方数，
        // 背包就是n，至于物品是否的有序或者无序放入就无所谓了，你随便放

        // 所以先遍历背包还是先遍历物品都是可以的

        /* 
            这里先遍历背包
         */

         // 先求符合条件的完全平方数
         vector data;
         for(int i=1;i<=n;i++) {
             if(i*i<=n) {
                 data.push_back(i*i);
             } else {
                 break;
             }
         }


         // 定义dp
         vector dp(n+1,INT_MAX);
        // 初始化
        dp[0]=0;
        // 代表容量为0的时候个数为0

        for(int i=0;i<=n;i++) { // 先遍历背包，不用初始化，因为背包容量为0，肯定放不下
            for(int j=0;j=data[j]) {
                  dp[i] = min(dp[i],dp[i-data[j]]+1);
               }
            }
        }

         return dp[n];

    }
};

状态压缩过程

要考虑插入顺序的完全背包问题

博客地址

总结

总结