银行贷款预测模型项目（Loan Prediction)（上）

项目背景

在房贷审批流程中，银行需要考虑贷款申请人的各种信息，比如家庭情况、经济情况、房子情况等等，经过综合分析这些因素后决定是否要贷款给申请人，即审批通过还是拒绝。

在大部分情况下，只需要一些基本的信息便可以大致判断申请人是否符合放贷资格。银行希望希望能够根据客户提供的详细信息（在线上填写申请表格），自动化贷款资格审批流程，并且将结果实时反馈给客户。

问题：贷款申请否通过？
这是一个生活中非常常见的二分类问题，基本上所有的银行每天都在处理这个问题，如果可以将这个过程自动化，便可一大大减少人力和时间成本。

建立假设（Hypothesis Generation）

很多项目流程都忽略了这一步，但是建立基本的假设更便于之后确定处理和分析数据资料的方向、范围。针对项目的问题：贷款申请是通过还是拒绝？ 需要考虑是什么因素对贷款有影响。 这里，因变量（Y）是贷款；自变量（X）是各种对贷款有影响的因素。

这里按照我们的对于放贷的理解，作出几点假设：
1）工资：工资越高，贷款更容易通过；
2）贷款期限和金额：贷款期限越短、金额越少的越容易通过；
3）EMI：monthly incom 还贷额占月收入比例,占比越低越容易通过；
4）贷款历史：已偿清之前贷款的申请人，贷款通过的机率更大。

数据探索性分析 EDA

1. 了解数据（Understand the Data）

#导入模块包
import pandas as pd 
import numpy as np                     # For mathematical calculations 
import seaborn as sns                  # For data visualization 
import matplotlib.pyplot as plt        # For plotting graphs 
%matplotlib inline 
import warnings                        # To ignore any warnings warnings.filterwarnings("ignore")

#读取数据
#Reading Data
train=pd.read_csv('train_ctrUa4K.csv')
test=pd.read_csv('test-file.csv')

#make a copy
train_original = train.copy()
test_original=test.copy()

#查看两个数据集有什么数据特征
print(train.columns)  #check the columns:Train.data has 'Loan_Status'
print(test.columns) 

# Print data types for each variable train.dtypes
print(train.dtypes)

print(train.shape)
print(test.shape)  #We have 614 rows and 13 columns in the train dataset and 367 rows and 12 columns in test dataset.

训练集Train 一共有614行，13列； Test测试集是367行，12列。 其中，训练集中每一列内容如下：

特征名称	数据格式	特征含义
Loan_ID	object	贷款ID
Gender	object	性别
Married	object	婚姻情况
Dependents	object	赡养人数
Education	object	教育情况
Self_Employed	object	是否自雇人士
ApplicantIncome	int64	申请人收入
CoapplicantIncome	float64	共同申请人收入
LoanAmount	float64	贷款金额
Loan_Amount_Term	float64	贷款期限
Credit_History	float64	信用记录
Property_Area	object	所在区域
Loan_Status	object	贷款状况

2. 单变量分析（Univariate Analysis）

2.1 目标变量

首先需要了解目标变量，贷款情况（通过还是拒绝）。由于这是个分类变量，因此分析方法采取计算频率、百分比和柱状图。

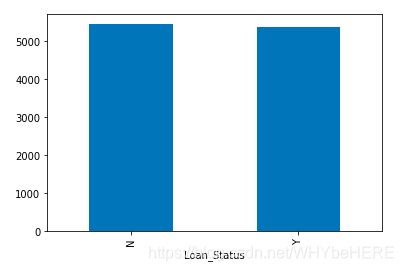
#univariate Analysis
print(train['Loan_Status'].value_counts())
# Normalize can be set to True to print proportions instead of number
print(train['Loan_Status'].value_counts(normalize=True))
train['Loan_Status'].value_counts().plot.bar()

• 422个申请人，约70%的贷款申请都是通过的。

2.2 自变量（Independent Variable）

了解完目标变量，我们接着分析其他的数据特征。
数据特征可以分成三类：分类特征、序数特征、数值特征：
关于各类数值的分析方法,可参考另一个笔记关于EDA的总结

2.2.1 分类特征 （Categorical Features)

#Independent Variable (Categorical)
plt.figure(1)
plt.subplot(221)
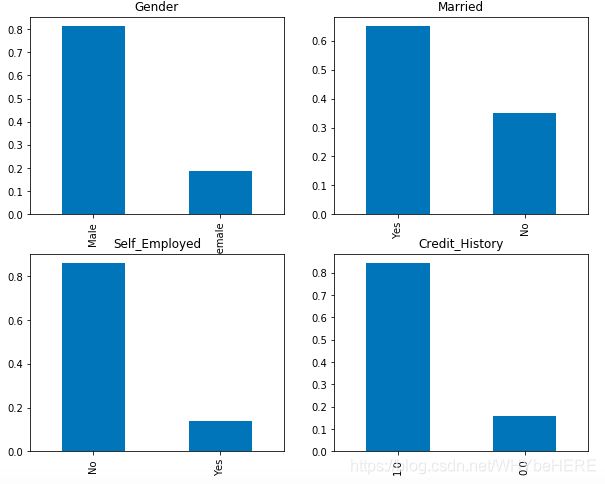
train['Gender'].value_counts(normalize=True).plot.bar(figsize=(10,8), title= 'Gender')
plt.subplot(222)
train['Married'].value_counts(normalize=True).plot.bar(title= 'Married')
plt.subplot(223)
train['Self_Employed'].value_counts(normalize=True).plot.bar(title= 'Self_Employed')
plt.subplot(224)
train['Credit_History'].value_counts(normalize=True).plot.bar(title= 'Credit_History')
plt.show()

-四个分类特征的柱状图可见：

• 近80%的申请人是男性，
• 大约65%的申请人是已婚；
• 15%是自雇人士
• 85%的申请人有信用记录。

2.2.2 序数特征 （Ordinal features:）

序数特征是分类特征中有一定顺序/规律的特征，比如教育程度，家庭人数等，所在区域等。

#ordinary 
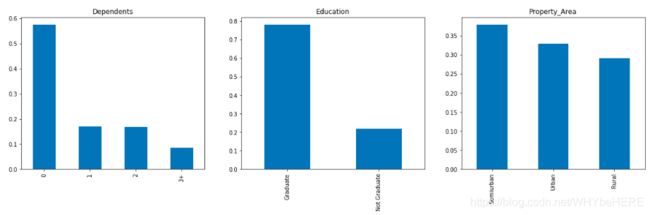
plt.figure(1)
plt.subplot(131)
train['Dependents'].value_counts(normalize=True).plot.bar(figsize=(20,5), title= 'Dependents')
plt.subplot(132)
train['Education'].value_counts(normalize=True).plot.bar(title= 'Education')
plt.subplot(133)
train['Property_Area'].value_counts(normalize=True).plot.bar(title= 'Property_Area')
plt.show()

train['Loan_Amount_Term'].value_counts(normalize=True).plot.bar(figsize=(10,5), title= 'Loan_Amount_Term)

• 大部分的申请人赡养人数为0，即没有需要他们提供生活资金的人；
• 大约80%的申请人是大学毕业生；
• 绝大部分的申请贷款的房产位于自半城市地区；
• 80%的贷款期限都是30年，不足10%的是15年 。

2.2.3 数值特征

在案例中，有三个重要的数值型变量特征：申请人收入ApplicantIncome, 共同申请人收入CoapplicantIncome, 贷款金额LoanAmount； 可以使用直方图和箱型图分析数值特征的分布情况。

# Numerical Variable （这只列一个ApplicantIncome，另外两个（CoapplicantIncome, LoanAmount）也是一样的。
plt.figure(1) 
plt.subplot(121) 
sns.distplot(train['ApplicantIncome']); 
plt.subplot(122) 
train['ApplicantIncome'].plot.box(figsize=(16,5)) 
plt.show()

• 申请人收入ApplicantIncome:
  从直方图可以看到整体分布是左偏的，并不符合正态分布，因此需要在后面一步中对数据做处理。
• 共同申请人收入CoapplicantIncome: 大部分共同申请的的收入在0-5000之间；和上面申请人收入的分布类似，也不是正态分布的，并且也有很多离散值。
  
• 贷款金额（Loan Amount): 贷款金额的分布接近于正太分布，但也有非常多的离散值。
  

3. 双/多变量分析（Bivariate Analysis)

回顾我们之前的假设：

• 高收入的申请人更高几率通过。
• 贷款金额越少越容易通过；
• 贷款期限越短越容易。

多变量分析方法可以根据特征的类型区分：数值特征之间、分类特征之间、分类特征和数值特征。

我们的目标是探索各种因素对目标变量（Loan_Status）的影响，在2.单变量分析里，我们了解了各类特征的基本情况，在多变量分析里，我们将这些特征和目标变量组合起来分析

3.1 分类特征&目标变量

使用堆积柱状图，直接将结果用百分比展示，查看各个分类特征对目标变量（Loan_Status）的影响。

#Target V & categorical V
Gender=pd.crosstab(train['Gender'],train['Loan_Status'])
Gender.div(Gender.sum(1).astype(float),axis=0).plot(kind='bar',stacked=True,figsize=(4,4))

• 已婚的申请人更容易获得通过；
• 赡养人数为1 或者3个以上的申请人，贷款通过率相似；
• 自雇和非自雇的申请人通过率相似；
• 有信用历史的人更容易获得贷款；
• 在半城市化区域的放贷申请，比农村和城市地区更容易通过；
• 大学毕业的申请人的通过率比没有毕业的要高。

3.2 数值特征&目标变量

对于数值型变量，最常用的分析方法是使用分类（Bin），比如将收入划分为低、中、高、超高四个类别，再画堆积图具体分析。 这里分析的数值特征有：申请人/共同申请人的收入；贷款金额

• 申请人收入

#mean
train.groupby('Loan_Status')['ApplicantIncome'].mean().plot.bar()

• 从平均数上看，贷款被拒绝和通过的申请人的平均收入一致，
• 单看平均数还不能证明申请人的收入并不影响贷款结果，需要进一步用BIN分析。

#bin
bins=[0,2500,4000,6000,81000]
group=['Low','Average','High','Very High']
train['Income_bin']=pd.cut(train['ApplicantIncome'],bins,labels=group)

Income_bin=pd.crosstab(train['Income_bin'],train['Loan_Status'])
Income_bin.div(Income_bin.sum(1).astype(float),axis=0).plot(kind='bar',stacked=True)
plt.xlabel('ApplicantIncome')
P = plt.ylabel('Percentage')

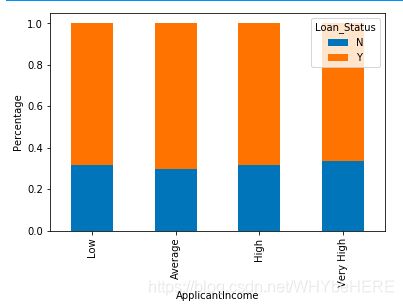
这里将收入分成了低、平均、高和非常高四类，可以发现四类的通过率都是一致的，意味着申请的收入并不影响贷款审批，这与我们之前的假设：’收入越高越容果通过‘不一致。

• 共同申请人收入（coapplicant Income ）
  
  同样的方法，将共同申请人的收入分成高中低三类。这里可以发现，共同申请人收入越低，反而更容易通过。这里与我们的经验常识不符。
  这可能是因为许多申请人并没有共同申请人（共同申请人为0）所以在审批流程中，这些案例无需考虑共同申请人的收入。

因此，我们在这里引进一个新的特征（汇总收入），将申请人和共同申请人的收入加总，作为一个新的变量。

• 汇总收入（Total_Income)

# combine the Applicant Income and Coapplicant Income 
#and see the combined effect of Total Income on the Loan_Status.
train['Total_Income']=train['ApplicantIncome']+train['CoapplicantIncome']

引入新特征（汇总收入）之后，我们可以看到，相比平均、高和非常高三列，第一列‘低’明显通过率更低，被拒绝的可能性接近60%。 总收入越低，贷款被拒绝的可能性越高。

• 贷款金额

使用相同的手段将贷款金额分成三组，图片展示的结果也和我们之前的假设一致，金额低的贷款更容易通过。第三列的蓝色部分（被拒绝）更高。

3.3 相关性

为了进一步比较各类特征的相关性，可以画热力图表示特征之间的相关性。由于很多模型（比如回归模型），只能处理数字，所以需要将文字类型的特征描述转换成数字：

首先，需要将有3个以上不同类别的特征，改成只有三个类别，并将转换成数值型；其次，需要把目标变量（Loan_status)的两个类别，转换成0和1。

train=train.drop(['Income_bin','Coapplicant_Income_bin','LoanAmount_bin','Total_Income_bin','Total_Income'],axis=1)

train['Dependents'].replace('3+',3,inplace=True)
test['Dependents'].replace('3+',3,inplace=True)
train['Loan_Status'].replace('N',0,inplace=True)
train['Loan_Status'].replace('Y',1,inplace=True)

#heat map
matrix=train.corr()
f, ax=plt.subplots(figsize=(9, 6))
sns.heatmap(matrix,vmax=.8,square=True,cmap='BuPu')

• 参考右边图例，颜色越深代表相关系数越接高。
• 相关性最高的变量是（申请人收入-贷款金额）和（贷款历史-贷款情况）
• 贷款金额与共同申请人的收入也具有一定的相关性

4.处理缺失值和异常值

4.1缺失值处理

1. 列出所有特征缺失值个数
2. 插补缺失值：
   - 数值型变量特征使用中位数或者平均值
   - 分类变量用众数插补
3. 检查数据集是否还有缺失值

# 1. list out
print(train.isnull().sum())

性别、婚姻情况、亲属、是否自雇认识，贷款金额，贷款期限和贷款历史，这些特征都有缺失值。

# 2. fill the missing values:
train['Gender'].fillna(train['Gender'].mode()[0],inplace=True)
train['Married'].fillna(train['Married'].mode()[0],inplace=True)
train['Dependents'].fillna(train['Dependents'].mode()[0],inplace=True)
train['Self_Employed'].fillna(train['Self_Employed'].mode()[0],inplace=True)
train['Credit_History'].fillna(train['Credit_History'].mode()[0],inplace=True)

#  fill the missing values in Loan_Amount_Term
#print(train['Loan_Amount_Term'].value_counts()) #查看各种数据的次数统计
train['Loan_Amount_Term'].fillna(train['Loan_Amount_Term'].mode()[0], inplace=True)

# Numerical variable, use mean or median to impute the missing values.
train['LoanAmount'].fillna(train['LoanAmount'].median(), inplace=True)

根据每个特征的具体情况，采用不同的方法处理缺失值。

• 众数mode()
• 中位数 median()
• 平均数 mean()

# 3. check
train.isnull().sum()

#using the method to replace the test.file
test['Gender'].fillna(train['Gender'].mode()[0],inplace=True)
test['Married'].fillna(train['Married'].mode()[0],inplace=True)
test['Dependents'].fillna(train['Dependents'].mode()[0],inplace=True)
test['Self_Employed'].fillna(train['Self_Employed'].mode()[0],inplace=True)
test['Credit_History'].fillna(train['Credit_History'].mode()[0],inplace=True)
test['Loan_Amount_Term'].fillna(train['Loan_Amount_Term'].mode()[0],inplace=True)
test['LoanAmount'].fillna(train['LoanAmount'].median(),inplace=True)

最后检查是否处理完所有缺失值，同时测试集的缺失值也要用同样方法处理.

4.2 离散值处理

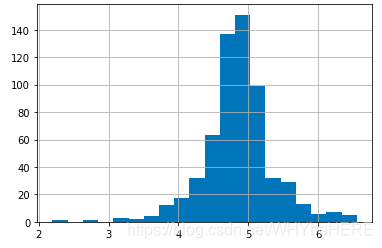
根据之前的分析，案例中的数值特征有非常大的离散值，导致整体分布偏斜。最基本的解决方法是用对数log。对数变换几乎对小的数值没什么影响，但可以将大的数值降低。经过对数变换后，就可以得到一个正态分布图。

####Outliner
train['LoanAmount_log']=np.log(train['LoanAmount'])
train['LoanAmount_log'].hist(bins=20)
test['LoanAmount_log']=np.log(test['LoanAmount'])

数据集经过分析和预处理，接下来就可以开始特征工程和建立模型。下篇链接

参考链接：Loan Prediction Practice Problem