Big Mart Sales prediction 商场销售预测分析项目

---

一、项目介绍

该项目目的是建立一个模型去预测每个产品在具体商场的销售情况，以协助决策者提高整体的销售情况。

数据集介绍：
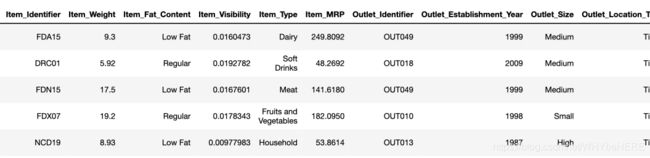
BigMart数据集收集了2013年不同城市中10个商场、1559个产品的销售数据。训练集和测试集一共是14204行，12列的数据。

数据集字段含义：

名称	类型	含义
Item_Identifier	object	物品识别号
Item_Weight	float64	物品种类
Item_Fat_Content	object	物品脂肪含量
Item_Visibility	float64	物品可见度
Item_Type	object	物品类型
Item_MRP	float64	物品MRP
Outlet_Identifier	object	商场识别号
Outlet_Establishment_Year	int64	商城成立年份
Outlet_Size	object	商城大小
Outlet_Location_Type	object	商城位置
Outlet_Type	object	商场类型
Item_Outlet_Sales	float64	物品商场销量（目标变量）

问题和数据集下载链接

---

二、建立假设（部分）

可以从店铺、产品、顾客、整体情况四个角度建立假设，虽然一些假设不一定能用数据去证明和测试，但是这个过程有助于我们去理解问题。

• 店铺
  • 城市类型：位于城市/一线城市的商店有较高的销售额，因为当地人们的收入水平较高。
  • 位置：受欢迎的商业区比其他地方的销售额应该更高。
  • 商店容量：规模很大的商店应该有更高的销售额，因为它们就像一站式商店，人们更喜欢从一个地方得到所有东西
  • 位置：位于热门市场的商店应该有更高的销售额，因为更容易接近客户。
• 产品
  • 物品类型：与特定用途产品相比，食物、日用品应具有更高的销售倾向。
  • 陈列区：商店里货架大的产品可能会先引起注意，卖得更多。
  • 可见性：产品在店内的位置会影响销售。在入口处的那些会首先吸引顾客的眼球，而不是后面的。
  • 价格：价格会影响产品的销售额，越贵的产品越少人购买。
• 顾客情况
  • 工作概况：与入门级或中高层员工相比，在高管级别工作的客户有更高的机会购买大额产品。
  • 家庭规模：家庭成员越多，顾客购买产品的花费就越大
  • 过去的购买历史：这些信息的可用性可以帮助我们确定用户购买产品的频率。
• 宏观层面的假设
  • 环境：如果政府宣称环境是安全的，顾客就更有可能购买产品而不必担心它是否环保。
  • 经济增长：如果当前经济持续增长，人均收入会上升，因此消费者的购买力也会增加。

三、数据探索分析

1.导入数据

关于数据，有几点是需要知道的：

• 数据的维度（Dimensions of Data），一共有几行几列数据，.shape()
• 数据特征（Features of Data），每组数据个代表什么意思。
• 数据结构（Structure of Data），是数值型还是类别型？各有多少？
• *合并训练集和测试集（根据需要）：这里两个数据集是分开的，为了减少重复工作，可以先将两个数据集合并，一起做数据处理，之后再分开。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

#读取数据
train=pd.read_csv('train_v9rqX0R (1).csv')
test=pd.read_csv('test_AbJTz2l.csv')

## 合并两个报表 
Features=['Item_Identifier', 'Item_Weight', 'Item_Fat_Content', 'Item_Visibility',
       'Item_Type', 'Item_MRP', 'Outlet_Identifier',
       'Outlet_Establishment_Year', 'Outlet_Size', 'Outlet_Location_Type',
       'Outlet_Type']
combine=pd.merge(train,test,on=Features, how='outer')
print(combine.shape)

合并两个数据表后，得到了一个14204行，12列的数据集。

combine.head()

2. 单变量分析

按照特征的下面类别做单变量分析。

分类类型（7）	Item_Identifier物品标识符、Item_Fat_Content脂肪含量、Item_Type物品种类、Outlet_Identifier商场标识符、Outlet_Size商场大小、Outlet_Location_Type位置、Outlet_Type商场类型
浮点类型(4)	Item_Weight 物品重量、Item_Visibility 物品可见度、Item_MRP 物品MRP、Item_Outlet_Sales 销售
数值类型（1）	Outlet_Establishment_Year int64 商场成立年份

2.1) 分类特征

a) Item_Fat_Content‘ 脂肪含量（重复名字处理）

#画出直方图看数据情况
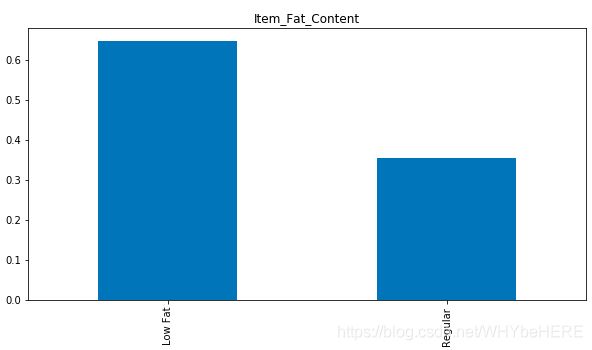
combine['Item_Fat_Content'].value_counts(normalize=True).plot.bar(figsize=(10,5), title= 'Item_Fat_Content')

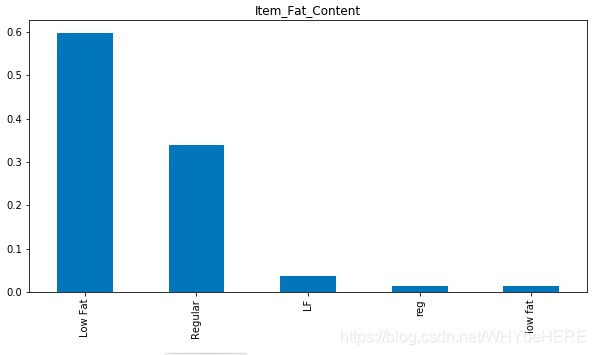
脂肪含量中有重复的名字，Low Fat、LF和 low fat; Regular 和reg。一共分成两类，但是出现了五类，需要替换名字。

# ！！有重复的不同名字
combine['Item_Fat_Content'].replace({'LF':'Low Fat','reg':'Regular','low fat':'Low Fat'},inplace=True)

#确认结果
combine['Item_Fat_Content'].value_counts(normalize=True).plot.bar(figsize=(10,5), title= 'Item_Fat_Content')

可见产品中约有65%是低脂肪，35%是正常标准。

b) Item_Type物品类别

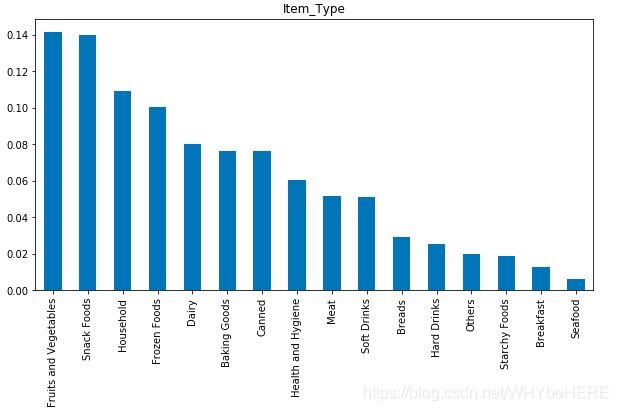
combine['Item_Type'].value_counts(normalize=True).plot.bar(figsize=(10,5), title= 'Item_Type')

• 一共有16个物品类别，水果蔬菜和零食最多，海鲜最少。

c) Outlet特征 (大小、位置、类型）

#观察Outlet特征情况
plt.figure(1)
combine['Outlet_Identifier'].value_counts(normalize=True).plot.bar(figsize=(20,5), title= 'Outlet_Identifier')

plt.figure(2)
plt.subplot(131)
combine['Outlet_Size'].value_counts(normalize=True).plot.bar(figsize=(20,5), title= 'Outlet_Size')
plt.subplot(132)
combine['Outlet_Location_Type'].value_counts(normalize=True).plot.bar(figsize=(20,5), title= 'Outlet_Location_Type')
plt.subplot(133)
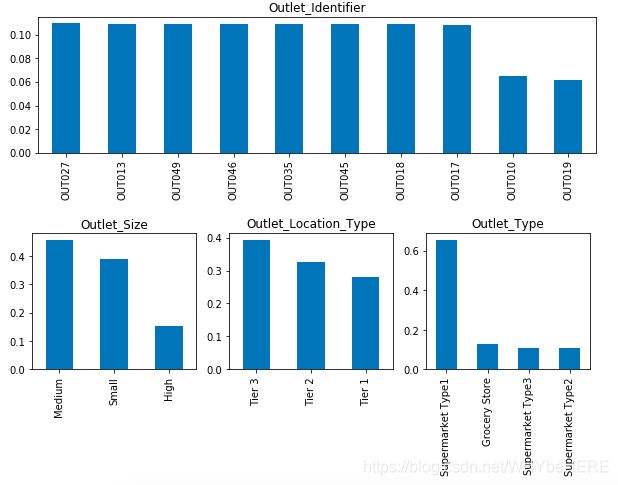
combine['Outlet_Type'].value_counts(normalize=True).plot.bar(figsize=(20,5), title= 'Outlet_Type')

# Outlet_Establishment_Year
plt.figure(3)
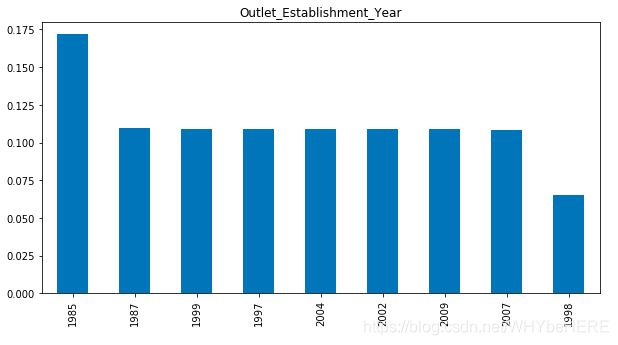
combine['Outlet_Establishment_Year'].value_counts(normalize=True).plot.bar(figsize=(10,5), title= 'Outlet_Establishment_Year')

• 从商场位置上看， Tier3城市观察到的数值是最多的。
• 超市类型Type1是最多的商场类型。
• 与其他年份相比，1998年设立的零售店的数据中观察到的数据较少。

2.2) 数值特征

一共有四个数值特征，可以画直方图看它们各自的分布情况。

1. Item_Outlet_Sales 销售量 （目标变量）
2. Item_Weight 物品重量
3. Item_Visibility 物品可见度
4. Item_MRP 物品MRP值

import seaborn as sns

plt.figure(1)
plt.subplot(221)
sns.distplot(combine['Item_Outlet_Sales'])
plt.subplot(222)
sns.distplot(combine['Item_Weight'])
plt.subplot(223)
sns.distplot(combine['Item_Visibility'])
plt.subplot(224)
sns.distplot(combine['Item_MRP'])

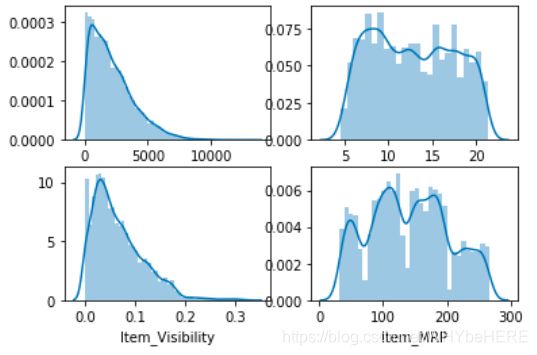
• 右上角的物品重量的分布没有明确区别。
• 物品可见度（左下）可见分布是向右偏的，需要进行转换改变其偏度，而且有不少值是0。
• 物品MRP（右下角）可以清楚地看到有四组不同的产品分布。

3. 多变量分析

3.1) 目标变量（销量）VS数值特征

由于两个变量都是数值型，可以用scatter plots 用散点图观察变量之间的关系。

#物品重量 和 销售量的相关性
plt.figure(1)
fig,ax=plt.subplots(figsize=(10,2.5))
ax.scatter(combine['Item_Weight'], combine['Item_Outlet_Sales'],color='pink')

#物品可见度 和 销售量的相关性
plt.figure(2)
fig,ax=plt.subplots(figsize=(10,2.5))
ax.scatter(combine['Item_Visibility'], combine['Item_Outlet_Sales'],color='pink')
#物品可见度 和 销售量的相关性

# tem_MRP 和销量相关性
plt.figure(3)
fig,ax=plt.subplots(figsize=(10,2.5))
ax.scatter(combine['Item_MRP'], combine['Item_Outlet_Sales'],color='pink')

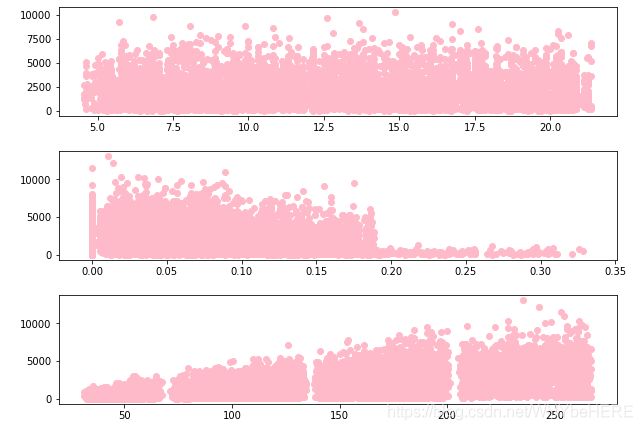
• 图1: Item_Outlet_的销售额分布在整个Item_重量范围内，两者似乎没有任何管来呢
• 图2: 在Item_Visibility和Item_Outlet_Sales中，Item_Visibility=0.0处有一系列点，这很奇怪，因为没有物品是看不见的。我们将在以后阶段处理这个问题。
• 图3: Item_MRP vs Item_Outlet_Sales：我们可以清楚地看到4个部分的价格，它们可以用于特征工程，以创建一个新的变量。

3.2) 目标变量（销量）VS分类特征

a) 物品类别VS销量关系

#物品类别和销量关系
import seaborn as sns
plt.figure(1)
fig,ax=plt.subplots(figsize=(20,8))
sns.set(style="whitegrid")
sns.boxenplot(x=combine['Item_Type'], y=combine['Item_Outlet_Sales'],scale="linear",color="yellow")

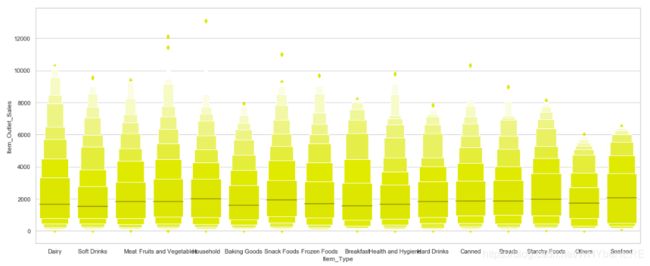
• Other 和 Seafood 的销量比较少，水果和蔬菜相对较高。
• 商品类别和销量没有明显的相关性，

b) 物品脂肪含量VS销量关系

#脂肪含量
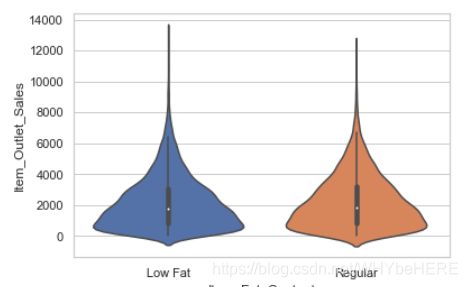
sns.violinplot(x=combine['Item_Fat_Content'], y=combine['Item_Outlet_Sales'])

• 脂肪含量的高低和销量没有明显的关系。

c) 商店情况VS销量

#商店编号
plt.figure(1)
fig,ax=plt.subplots(figsize=(10,3))
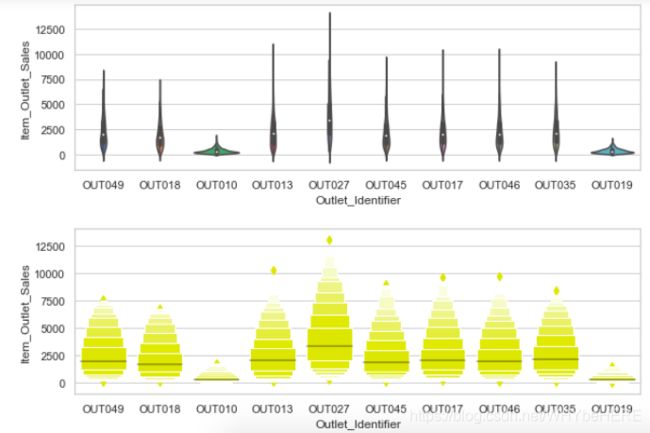
sns.violinplot(x=combine['Outlet_Identifier'], y=combine['Item_Outlet_Sales'])
plt.figure(2)
fig,ax=plt.subplots(figsize=(10,3))
sns.set(style="whitegrid")
sns.boxenplot(x=combine['Outlet_Identifier'], y=combine['Item_Outlet_Sales'],scale="linear",color="yellow")

• OUT010 和 OUT019 两个商店和其他的明显不一样。
• OUT027 的销量跨度是最大的

f,ax=plt.subplots(1,3,figsize=(18,3))
#商店大小
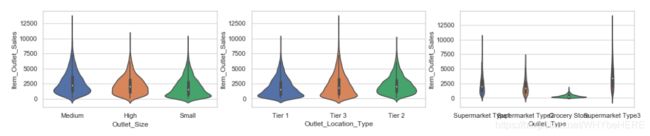
sns.violinplot(x=combine['Outlet_Size'], y=combine['Item_Outlet_Sales'],ax=ax[0])
#位置
sns.violinplot(x=combine['Outlet_Location_Type'],y=combine['Item_Outlet_Sales'],ax=ax[1])
#商店类型
sns.violinplot(x=combine['Outlet_Type'], y=combine['Item_Outlet_Sales'],ax=ax[2])

• Grocery Store 的销量数值都明显比其他类型的商店低

4. 缺失值处理

4.1）查找缺失值

#查缺失值
print(combine.isnull().sum())

#查看Item_Visibility有多少个0
(combine['Item_Visibility'] == 0).value_counts()

三个特征有缺失情况：Item_Weight 2439; Outlet_Size 4016; Item_Visibility 有879个值等于0。

4.2）缺失值处理

• 根据Item_Identifier， 将Item_Weight 和 Item_Visibility的缺失值用均值替换；

#利用数据透视表计算平均值,根据Item_Identifier,计算出重量、可见度的均值
pd.pivot_table(combine,index=['Item_Identifier'],values=['Item_Weight','Item_Visibility'],aggfunc=[np.mean])

#处理Item_Weight
item_avg_weight = combine.pivot_table(values='Item_Weight', index='Item_Identifier') 
miss_bool = combine['Item_Weight'].isnull() 
combine.loc[miss_bool,'Item_Weight'] = combine.loc[miss_bool,'Item_Identifier'].apply(lambda x: item_avg_weight.loc[x])

#处理等于0的Item_Visibility
visibility_avg = combine.pivot_table(index='Item_Identifier', values='Item_Visibility')
miss_bool = (combine['Item_Visibility'] == 0)#这里是要替代0值，不是空值。
combine.loc[miss_bool,'Item_Visibility'] =combine.loc[miss_bool,'Item_Identifier'].apply(lambda x: visibility_avg.loc[x])

• 根据Outlet_Identifier找出每个商店的Size， 并将缺失的4016个Outlet_Size补充完整。

#查看每个商店的大小
pd.crosstab(combine.Outlet_Identifier,combine.Outlet_Size).T.style.background_gradient(cmap='summer_r')

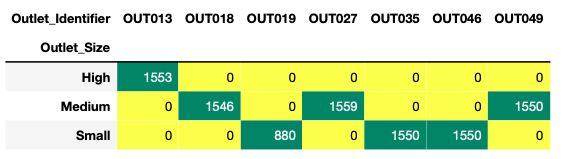
结果得出7个商店的Size, 表明有3个商店的Size是缺失的，分别是OUT010、OUT017、OUT045因此不能直接使用identifier，接下来改变使用Outlet_Type 做分析:

#查看大小和类型的关系
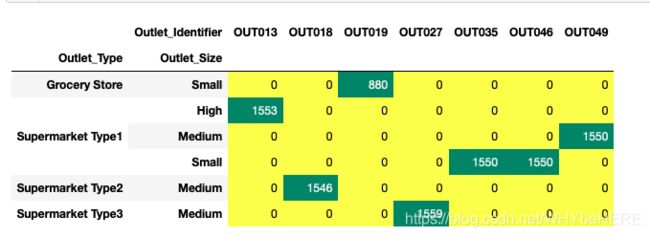
pd.crosstab(combine.Outlet_Identifier,[combine.Outlet_Type,combine.Outlet_Size]).T.style.background_gradient(cmap='summer_r')

• Grocery Store： small
• Supermarket Type1: 最多是SMall
• Supermarket Type2 和 Type3 都是Medium

再继续查看每个商店的类型

#查看10个商店的类型
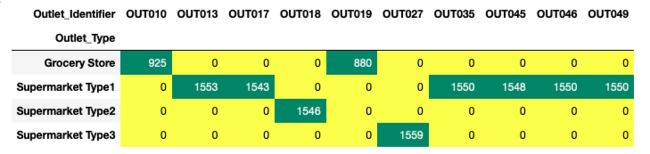
pd.crosstab(combine.Outlet_Identifier,combine.Outlet_Type).T.style.background_gradient(cmap='summer_r')

• OUT010 是 grocery store 和OUT019 一样，联系之前分析Sales情况时，两个店铺的情况也是一样的。所以OUT010的Size 和OUT019一样， 为SMALL
• OUT017、OUT045 是Supermarket Type1， 取众数Small替代缺失值。

## 替换方法
combine.loc[(combine.Outlet_Size.isnull())&(combine.Outlet_Identifier=='OUT010'),'Outlet_Size']='Small'
combine.loc[(combine.Outlet_Size.isnull())&(combine.Outlet_Identifier=='OUT017'),'Outlet_Size']='Small'
combine.loc[(combine.Outlet_Size.isnull())&(combine.Outlet_Identifier=='OUT045'),'Outlet_Size']='Small'

4.3）检查结果

#检查结果
print(combine.isnull().sum())

#画图观察结果
plt.figure(2)
plt.subplot(221)
sns.distplot(combine['Item_Weight'])
plt.subplot(222)
sns.distplot(combine['Item_Visibility'])

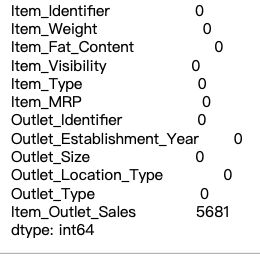
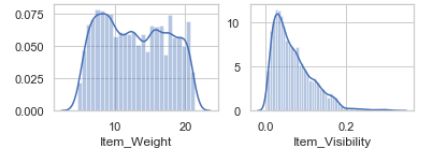
缺失值都处理完，数据分布比原来的更加平滑，Visibility 的0值也去掉了。

四、特征工程

1.提取新特征

在原始数据集中，为了再提取出更多有用的数据信息，接着介绍5个新特征：Item_Type_new、Item_category、Outlet_Years、price_per_unit_wt、Item_MRP_clusters。

1.1) Item_Type_new 减少物品类别

在之前的分析中，物品有十几个类别，不方便后续分析，这里将这些类别根据保存时间简单分成两类：perishable（易腐烂的）、non_perishable（不易腐烂的）

perishable = ["Breads", "Breakfast", "Dairy", "Fruits and Vegetables", "Meat", "Seafood"]
non_perishable = ["Baking Goods", "Canned", "Frozen Foods", "Hard Drinks", "Health and Hygiene", "Household", "Soft Drinks"]

newtype=[]
for z in range(0,len(combine['Item_Type'])):
    z = combine['Item_Type'][z]
    if z in perishable:
        newtype.append("perishable") 
    else:
        newtype.append("non_perishable")
        
combine['Item_Type_new']=newtype

1.2) Item_category

通过观察Item_Identifier的结构，分别是由两个字母和数字构成，开头两个字母是‘DR’, ‘FD’, and ‘NC’，即饮料、食物和消费品。从这里，我们可以提取出一个新的特征：

## 取Item_Identifier的前两位作为新特征
combine['Item_category']=[x[:2] for x in combine['Item_Identifier']]

#观察各类的观测值数量。
combine["Item_category"].value_counts()

#查看每类具体有什么类型商品
pd.pivot_table(combine,index=["Item_Type"],values=["Item_Identifier"],columns=["Item_category"],aggfunc='count')

1.3) Outlet_Years和 price_per_unit_wt

继续创建下面两个特征：

• Outlet_Years：商店经营了多少年。相比起具体的建立年份，经营了多少年对我们分析更有价值。
• price_per_unit_wt ：每单位重量的价格（Item_MRP/Item_Weight）

#假设今年是2013年，和课程假设一致
combine['Outlet_Years']=2013-combine['Outlet_Establishment_Year']
combine['price_per_unit_wt']=combine['Item_MRP']/combine['Item_Weight']

1.4) Item_MRP_clusters

在之前Item_MRP 和 Item_Outlet_Sales 的分析中，明显看出整体被分成了四个区，我们这里也重新根据Item_MRP 分四组。

bins=[0,69,136,203,300]
group=['1st','2nd','3rd','4th']
combine['Item_MRP_clusters']=pd.cut(combine['Item_MRP'],bins,labels=group)

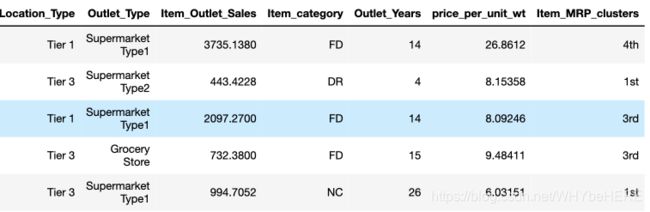
#查看结果
combine.head(5)

2. 特征转换

对于一些文字型的特征，需要将它们转换成数值型。比如位置、商品/商店类型等。这里使用两种常用的方法：

• 标签编码：将变量中的每个类别转换成一个数字
• 独热编码：分类变量的每个类别都转换为一个新的二进制列（1/0）

#标签编码
from sklearn.preprocessing import LabelEncoder
LE = LabelEncoder()
laber_features = ['Item_Fat_Content','Outlet_Size','Outlet_Location_Type','Item_Type_new','Item_MRP_clusters']
for i in laber_features:
    combine[i] = LE.fit_transform(combine[i])

# 独热编码
#One Hot Coding:
combine['Outlet'] = combine['Outlet_Identifier'] #结果需要保留Outlet_Identifier
combine = pd.get_dummies(combine, columns=['Outlet','Outlet_Type','Item_category'])

#删除多余的两列
combine.drop(['Item_Type','Outlet_Establishment_Year'],axis=1,inplace=True)

部分结果显示：除了两个Identifier, 其余特征都转换为数字。

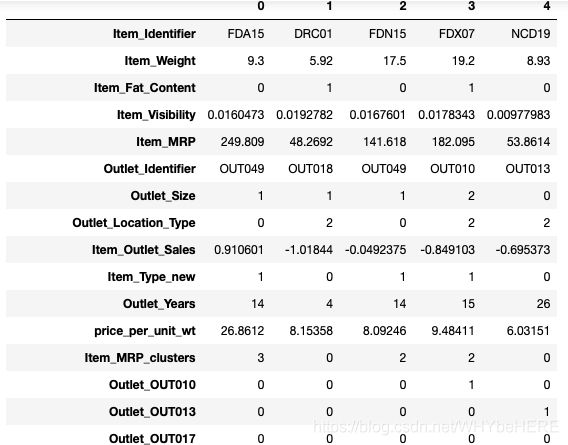
3. 数据预处理

1. 消除偏态（Removing Skewness）

price_per_unit_wt 和 Item_Visibility 的都是右偏态，为了令两个特征分布更偏向于正态分布，使用对数转换，这里使用log+1是为了避免有0的情况。（log0没有意义）

#Removing Skewness
combine['Item_Visibility']=np.log((combine['Item_Visibility']+1).astype('float'))
combine['price_per_unit_wt']=np.log((combine['price_per_unit_wt']+1).astype('float'))
#查看结果
combine['price_per_unit_wt'].hist(bins=20)
combine['Item_Visibility'].hist(bins=20)

	对数转换前	对数转换后
Item_Visibility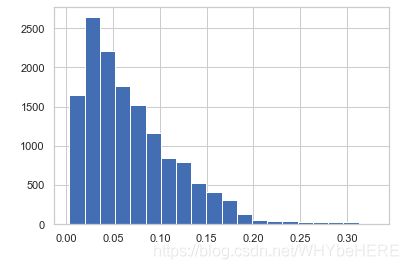
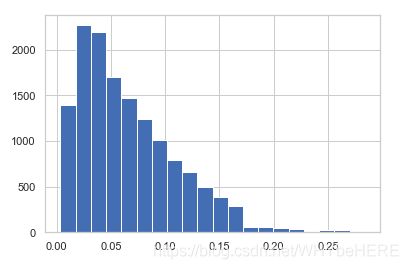price_per_unit_wt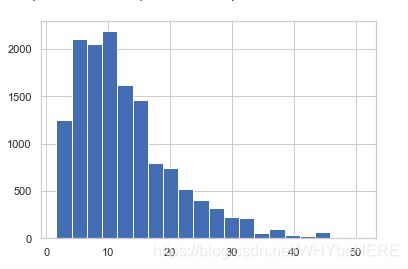

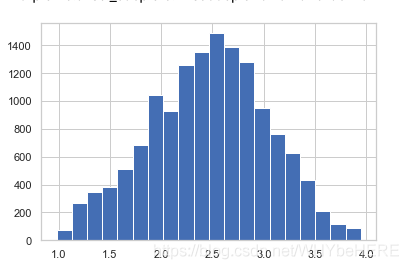2. 归一化

数值型特征，比如重量、价格等，范围都不一样，所以需要把所有的数值型特征都缩放到[0,1]之间。

#Scaling numeric predictors
from sklearn.preprocessing import MinMaxScaler
combine['Item_Weight'] = MinMaxScaler().fit_transform(combine[['Item_Weight']])
combine['Item_MRP'] = MinMaxScaler().fit_transform(combine[['Item_MRP']])
combine['price_per_unit_wt'] = MinMaxScaler().fit_transform(combine[['price_per_unit_wt']])
combine['Item_Visibility'] = MinMaxScaler().fit_transform(combine[['Item_Visibility']])
combine['Outlet_Years'] = MinMaxScaler().fit_transform(combine[['Outlet_Years']])

#查看结果
combine.describe().T #后面加T转置表格

选中的数值型特征都在0-1的范围内。

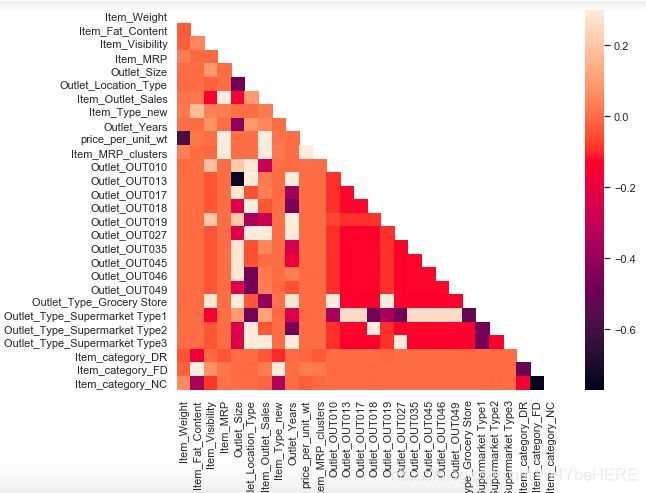
3. 相关性分析（Correlated Variables）

#Correlated Variables
corr = combine.corr()
mask = np.zeros_like(corr)
mask[np.triu_indices_from(mask)] = True
with sns.axes_style("white"):
    f, ax = plt.subplots(figsize=(10, 8))
    ax = sns.heatmap(corr, mask=mask, vmax=.3, square=True)

4. 导出数据

#切分数据集
train = combine.loc[combine['Item_Outlet_Sales'].notnull()]
test = combine.loc[combine['Item_Outlet_Sales'].isnull()]

#删掉test 中多余的列
test.drop(['Item_Outlet_Sales'],axis=1,inplace=True)

#导出数据
train.to_csv("train_modified.csv",index=False)
test.to_csv("test_modified.csv",index=False)

print(train.shape,test.shape)

结果输出： (8523, 30)(5681, 29)
训练集有8523条数据，测试集有5681条数据。

#查看
combine.dtypes

#结果输出

Item_Identifier                   object
Item_Weight                      float64
Item_Fat_Content                   int64
Item_Visibility                  float64
Item_MRP                         float64
Outlet_Identifier                 object
Outlet_Size                        int64
Outlet_Location_Type               int64
Item_Outlet_Sales                float64
Item_Type_new                      int64
Outlet_Years                     float64
price_per_unit_wt                float64
Item_MRP_clusters                  int64
Outlet_OUT010                      uint8
Outlet_OUT013                      uint8
Outlet_OUT017                      uint8
Outlet_OUT018                      uint8
Outlet_OUT019                      uint8
Outlet_OUT027                      uint8
Outlet_OUT035                      uint8
Outlet_OUT045                      uint8
Outlet_OUT046                      uint8
Outlet_OUT049                      uint8
Outlet_Type_Grocery Store          uint8
Outlet_Type_Supermarket Type1      uint8
Outlet_Type_Supermarket Type2      uint8
Outlet_Type_Supermarket Type3      uint8
Item_category_DR                   uint8
Item_category_FD                   uint8
Item_category_NC                   uint8
dtype: object

五、建模

1. 切分数据集

#导入清洗好的数据
train=pd.read_csv('train_modified.csv')
test=pd.read_csv('test_modified.csv')

#提取两个Identifier
test_ID=test[['Item_Identifier','Outlet_Identifier']]
train_ID=train[['Item_Identifier','Outlet_Identifier']]

test=test.drop(['Item_Identifier','Outlet_Identifier'],1)
train=train.drop(['Item_Identifier','Outlet_Identifier'],1)

#数据集切分
X=train.drop('Item_Outlet_Sales',1)
y=train.Item_Outlet_Sales
from sklearn.model_selection import train_test_split
#import LogisticReression and accuracy_score from sklearn and fit the lofistic regression model
x_train, x_cv, y_train, y_cv = train_test_split(X,y, test_size =0.3)

2. 模型选择

def mae(y_true, y_pred):
    return np.mean(abs(y_true - y_pred))

def fit_and_evaluate(model):
    
    # Train the model
    model.fit(x_train, y_train)
    
    # Make predictions and evalute
    model_pred = model.predict(x_cv)
    model_mae = mae(y_cv, model_pred)
    
    # Return the performance metric
    return model_mae

2.1） LinearRegression

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr_mae = fit_and_evaluate(lr)

print('Linear Regression Performance on the test set: MAE = %0.4f' % lr_mae)

Linear Regression Performance on the test set: MAE = 857.2215

2.2） RandomForestRegressor

from sklearn.ensemble import RandomForestRegressor
random_forest = RandomForestRegressor(random_state=60)
random_forest_mae = fit_and_evaluate(random_forest)

print('Random Forest Regression Performance on the test set: MAE = %0.4f' % random_forest_mae)

Random Forest Regression Performance on the test set: MAE = 808.5536

2.3） KNeighborsRegressor

from sklearn.neighbors import KNeighborsRegressor
knn = KNeighborsRegressor(n_neighbors=10)
knn_mae = fit_and_evaluate(knn)

print('K-Nearest Neighbors Regression Performance on the test set: MAE = %0.4f' % knn_mae)

K-Nearest Neighbors Regression Performance on the test set: MAE = 826.7566

2.4） GradientBoostingRegressor

from sklearn.ensemble import GradientBoostingRegressor
gradient_boosted = GradientBoostingRegressor(random_state=60)
gradient_boosted_mae = fit_and_evaluate(gradient_boosted)

print('Gradient Boosted Regression Performance on the test set: MAE = %0.4f' % gradient_boosted_mae)

Gradient Boosted Regression Performance on the test set: MAE = 784.4336

2.5） XGBRegressor

from xgboost import XGBRegressor
Xgboost= XGBRegressor(random_state=60)
Xgboost_mae = fit_and_evaluate(Xgboost)

print('XGBRegressor Performance on the test set: MAE = %0.4f' % Xgboost_mae)

XGBRegressor Performance on the test set: MAE = 752.6979

2.6）模型对比

from IPython.core.pylabtools import figsize

plt.style.use('fivethirtyeight')
figsize(8, 6)

# Dataframe to hold the results
model_comparison = pd.DataFrame({'model': ['Linear Regression',
                                           'Random Forest', 'Gradient Boosted',
                                            'K-Nearest Neighbors','XGBRegressor'],
                                 'mae': [lr_mae, random_forest_mae, 
                                         gradient_boosted_mae, knn_mae,Xgboost_mae]})

# Horizontal bar chart of test mae
model_comparison.sort_values('mae', ascending = False).plot(x = 'model', y = 'mae', kind = 'barh',
                                                           color = 'red', edgecolor = 'black')

# Plot formatting
plt.ylabel(''); plt.yticks(size = 14); plt.xlabel('Mean Absolute Error'); plt.xticks(size = 14)
plt.title('Model Comparison on Test MAE', size = 20)

五个模型中，XGBRegressor表现最好。

#查看模型具体参数
Xgboost

4. 模型调参

4.1）RandomizedSearchCV

先用random search可以找出大概找到合理的参数位置, 在用GridSearchCV查找最佳的参数。

from sklearn.model_selection import RandomizedSearchCV, GridSearchCV

# 设置参数
n_estimators = [50, 100, 250]
max_depth = [5, 10]
min_child_weight = [1, 3, 6]
learning_rate = [0.1, 0.2, 0.3]

hyperparameter_grid = {'n_estimators': n_estimators,
                       'max_depth': max_depth,
                       'min_child_weight': min_child_weight,
                       'learning_rate': learning_rate}
                       
# Create the model to use for hyperparameter tuning
model= XGBRegressor(random_state = 60)

# Set up the random search with 4-fold cross validation
random_cv_xgboost = RandomizedSearchCV(estimator=model,
                               param_distributions=hyperparameter_grid,
                               cv=4, n_iter=25, 
                               scoring = 'neg_mean_absolute_error',
                               n_jobs = -1, verbose = 1, 
                               return_train_score = True,
                               random_state=60)

#找出最佳的模型
random_model=random_cv_xgboost.best_estimator_
random_model

#查看新模型的结果
random_model_pred=random_model.predict(x_cv)
print('RandomSearc model performance on the test set:   MAE = %0.4f.' % mae(y_cv, random_model_pred))

RandomSearc model performance on the test set: MAE = 680.8172.

MAE降低到680.8172。

4.2) GridSearchCV (n_estimator)

用GridSearchCV查找最佳的n_estimator。

# 对比n_estimator在20-100范围内的结果
trees_grid = {'n_estimators': [20,30,40,50,60,70,100]}

#这里导入上面的random_model的模型参数，删掉n_estimator。
model = XGBRegressor(base_score=0.5, booster='gbtree', colsample_bylevel=1,
             colsample_bynode=1, colsample_bytree=1, gamma=0,
             importance_type='gain', learning_rate=0.1, max_delta_step=0,
             max_depth=5, min_child_weight=3, missing=None,
             n_jobs=1, nthread=None, objective='reg:linear', random_state=60,
             reg_alpha=0, reg_lambda=1, scale_pos_weight=1, seed=None,
             silent=None, subsample=1, verbosity=1)

grid_search = GridSearchCV(estimator = model, param_grid=trees_grid, cv = 4, 
                           scoring = 'neg_mean_absolute_error', verbose = 1,
                           n_jobs = -1, return_train_score = True)
                           
# 训练模型
grid_search.fit(X, y)

将结果可视化

from IPython.core.pylabtools import figsize
# Get the results into a dataframe
results = pd.DataFrame(grid_search.cv_results_)

# Plot the training and testing error vs number of trees
figsize(8, 4)
plt.style.use('fivethirtyeight')
plt.plot(results['param_n_estimators'], -1 * results['mean_test_score'], label = 'Testing Error')
plt.plot(results['param_n_estimators'], -1 * results['mean_train_score'], label = 'Training Error')
plt.xlabel('Number of Trees'); plt.ylabel('Mean Abosolute Error'); plt.legend();
plt.title('Performance vs Number of Trees');

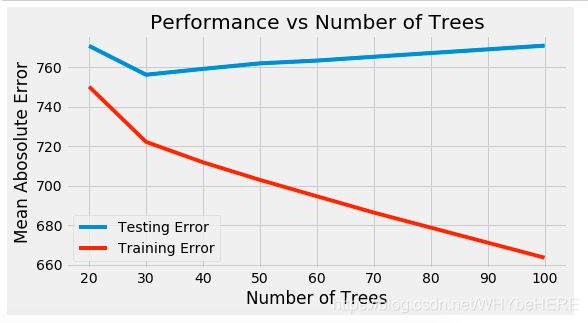
可见最佳的n_estimator是30，超过30之后就有过拟合的现象。

5. 测试模型

1. 计算MAE值
   MAE：Mean Abosolute Error 平均绝对误差，是绝对误差的平均值。可以更好地反映预测值误差的实际情况。

model_30tree=grid_search.best_estimator_

thirtytree_pred=model_30tree.predict(x_cv)
print('thirtytree_pred model performance on the test set:   MAE = %0.4f.' % mae(y_cv, thirtytree_pred))

• 输出结果：thirtytree_pred model performance on the test set: MAE = 723.8820.

• 最后MAE结果为723.8820，比原来的752.6979下降了30。

2. 计算RMSE值
   根据参考文章使用RMSE（Root Mean Square Error）均方根误差方法。

from sklearn import metrics
print ("RMSE : %.4g" % np.sqrt(metrics.mean_squared_error(y_cv, thirtytree_pred)))

• 输出结果：RMSE : 1058

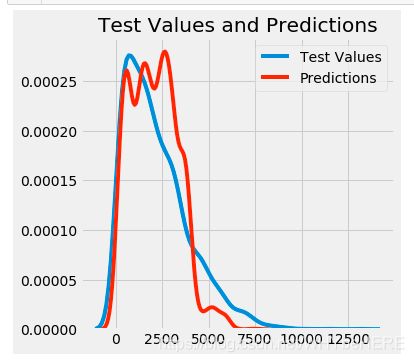
4. 预测和真实之间的差异图

figsize(5, 5)

# Density plot of the final predictions and the test values
sns.kdeplot(y_cv, label = 'Test Values')
sns.kdeplot(thirtytree_pred, label = 'Predictions')

# Label the plot
plt.xlabel('Energy Star Score'); plt.ylabel('Item_Outlet_Sales');
plt.title('Test Values and Predictions');

#导出结果
test_predition=model_30tree.predict(test)

submission=test_ID
submission['Outlet_Sales']=test_predition
submission.to_csv('Submission.csv')

6. 特征重要性

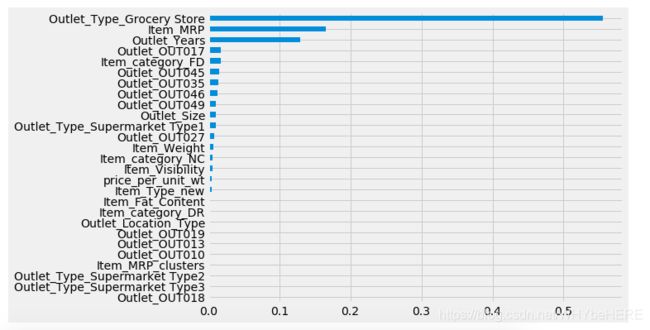
importances=pd.Series(model_30tree.feature_importances_, index=X.columns).sort_values(ascending=True) 
importances.plot(kind='barh', figsize=(8,6))

• 排名第一的是Outlt_Type_Grocery Store。在之前的双变量分析中，Grocery Store的销售情况和其他Supermarket类型的商店明显是两类分布，所以两类商店的销售情况差异很大。
• Item_MRP: 产品价格是造成销售额的重要因素。
• Outlet_Years 商店成立时间也是重要的特征之一。

六、总结

本项目从建立假设开始了解数据的基本情况；接着通过数据探索（单/双变量分析）深度挖掘和调整每项数据背后的信息；接着完成数据预处理和特征工程将数据信息进一步提炼；最后从5个模型结果中，选择了表现最好的XGBRegressor模型进行调参优化。

接下来还可以针对XGBRegressor的其他参数进行调整提升；或者根据特征重要性重新进行特征选择。

参考链接：
https://datahack.analyticsvidhya.com/contest/practice-problem-big-mart-sales-iii/#About
https://www.analyticsvidhya.com/blog/2016/02/bigmart-sales-solution-top-20/
欢迎大家纠错讨论～ 如果觉得这篇文章对你有帮助也请多多留言点赞哦！^ 0 ^