基于R class包进行近邻分析（KNN）

KNN 算法是 Cover 和 Hart 于1968 年提出一种基于统计的学习方法。所谓K最近邻，就是k个最近的邻居的意思，说的是每个样本都可以用它最接近的k个邻居来代表。等于就是把先数据通过特征空间属性，主要就是计算欧式距离，分为K个相近类别，后面的数据根据自己的属性划分到和自己属性最相似的类别上。

我们通过R语言来演示一下近邻分析（KNN），先导入我们的R包和数据，

library(class)
library(gmodels)
library(pROC)
library(ggplot2)
bc<-read.csv("E:/r/test/wdbc.csv",sep=',',header=TRUE)

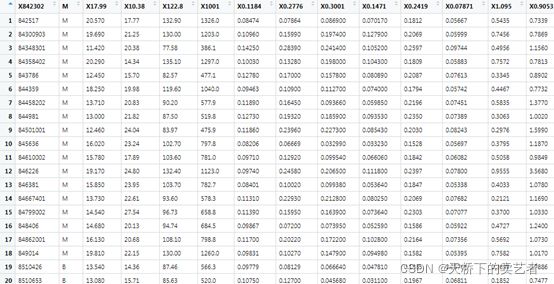
这是一个关于肿瘤数据(公众号回复：KNN数据，可以获得数据)，第一列是患者编号，第二列表示肿瘤是否是恶性的（M是恶性，B是良性），其他都是肿瘤的参数，有周长，直径，光滑度，凹凸点等数据，共有32个参数，有些数据很大20.5cm,有些才0.08cm。
删掉没用编号

bc<-bc[-1]

把性别转成因子，并且用0,1表示

bc$M<-ifelse(bc$M=="B",0,1)
bc$M<-factor(bc$M,levels = c(0,1))

对数据归一化处理（上一章有详细介绍），就是把数据变成0-1之间。

f1<-function(x){
  return((x-min(x)) / (max(x)-min(x)))
}
be<-as.data.frame(lapply(bc[2:31],f1))

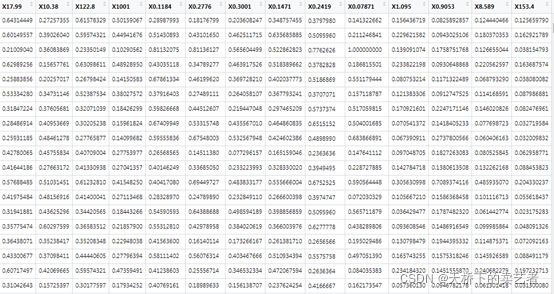
数据处理后，数据进行了压缩，变得具有比较性，我们把它分为训练集和验证集，因为本数据已经是随机分布的，所以我们这里就直接分类就可以了，注意一下，这分类的这两个数据集，是没有包含结局变量的。

train<-be[1:469,]
test<-be[470:568,]
train_lab<-bc[1:469,1]######获取训练集结局变量
test_lab<-bc[470:568,1]######获取验证集结局变量

使用KNN函数生成预测变量

pre<-knn(train = train,test = test,cl=train_lab,k=21)

生成预测值后，使用混淆矩阵对预测集和验证集进行比较

table<-CrossTable(x=test_lab,y=pre,prop.r = F)

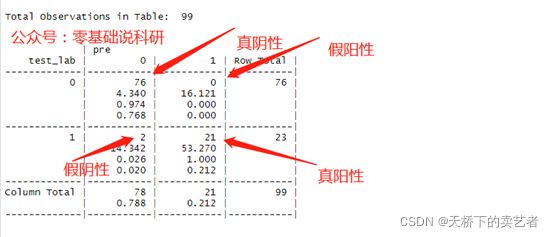
我们可以看到（上图）上方为预测结果，左侧为实际结果，斜线上的结果为预测正确的（真阴性和真阳性），预测为阴性实际是肿瘤的有2个（假阴性），预测是肿瘤实际是阴性的为0（假阳性），表明预测得还是蛮准的。我们来算一下auc

tp1<-table$t[2,2]###真阳性
tn1<-table$t[1,1]###真阴性
fn1<-table$t[2,1]###假阴性
fp1<-table$t[1,2]###假阳性
accuracy<-(tp1+tn1)/(tp1+fn1+fp1+tn1)
accuracy

敏感性和特异性

sen<-tp1/(tp1+fn1)###敏感性
sp<-tn1/(tn1+fp1)###特异性

表明预测得很准确，也可以通过pROC包的multiclass.roc函数来预测

multiclass.roc(response=test_lab,predictor =as.ordered(pre))

下面来进行一个比较重要的问题，KNN算法中,K是K个近邻，在上面的例子中我们的K取值21，那么K取值多少最合适？K取值多少可以AUC最高？
我们可以自己写个算法来算出合适的AUC值
假设K取值1-150之间，看哪个K值合适

n<-c(1:150)

编个function

auc1<-function(n){
  for(i in 1:n){
    pre<-knn(train = train,test = test,cl=train_lab,k=i)
    table<-CrossTable(x=test_lab,y=pre,prop.r = F)
    tp1<-table$t[2,2]###真阳性
    tn1<-table$t[1,1]###真阴性
    fn1<-table$t[2,1]###假阴性
    fp1<-table$t[1,2]###假阳性
    accuracy<-(tp1+tn1)/(tp1+fn1+fp1+tn1)
  }
  accuracy
}

这里要注意一下，这里直接把n带入function里是算不出结果的，会报错，因此还要把这个程序向量化

auc1<-Vectorize(auc1)
bg<-auc1(n)
bg

结果出来需要点时间，时间由你电脑的速度来定

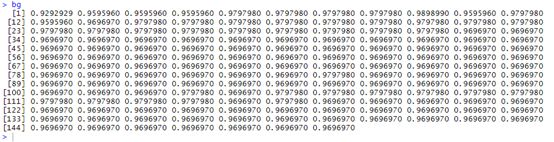
我们使用lapply函数来跑结果也是一样的

bf<-lapply(n,auc1)
bf<-as.matrix(bf)####把结果转成矩阵形式

得出结果后我们可以进行对结果可视化分析

qplot(n,bg,geom = c("point","smooth"))

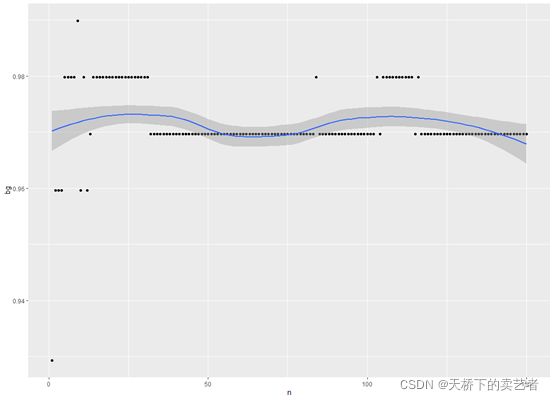
由上图可以知道，观察散点，随着K值不同，准确率还是有所不一样的，大约在K=10左右(就是图中位置最高的散点)，准确率最高。