运筹说 第39期 | 运输问题经典例题讲解
运输问题是针对生产与需求之间的关系,如何使供应链可以高效率低成本地进行与控制的问题。说到底这也是一个求最优解的问题,即如何在多种方案之中找到最优的一种方案。
通过前面的学习,我们了解到运输问题是一类特殊的线性规划问题,将单纯型法的思想用到运输问题的求解里,便得到了运输问题的表上作业法。首先确定初始方案,可选用西北角法、最小元素法或伏格尔法;其次进行解的最优性检验,有闭回路法和位势法两种基本方法;最后进行解的调整优化,直至求得最优解。
本期,小编选取五个运输问题的经典例题,包括产销平衡问题、产大于销问题、产小于销问题、弹性需求问题和中间转运问题进行详细讲解。
#1产销平衡的运输问题
1.问题描述
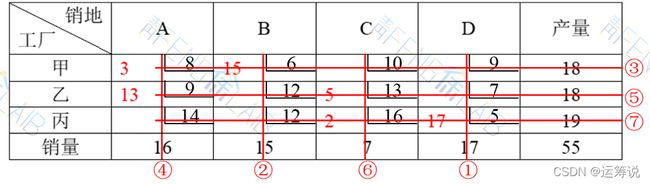
某公司下属有甲、乙、丙三个工厂,分别向A、B、C、D四个销地提供产品,产量、需求量及工厂到销售地的运价(单位:元/吨)如下表所示,求使费用最少的最佳运输方案。
2.问题解析
总产量=18+18+19=55
总销量=16+15+7+17=55
产量等于销量,即这是产销平衡的运输问题。直接采用表上作业法进行求解。
3.问题求解
(1)运用最小元素法确定初始方案,如下表所示。
(2)运用位势法对上述运输方案进行检验,检验数表如下。
因为存在检验数-2小于0,所以当前方案不是最优方案。
(3)进行解的调整优化,改进方案表如下所示。
用位势法对改进方案进行检验,得到改进方案的检验数表如下表。
此时所有非基变量的检验数都大于等于0,则当前方案是最优方案,最优方案如下表所示。
#2产大于销的运输问题
1.问题描述
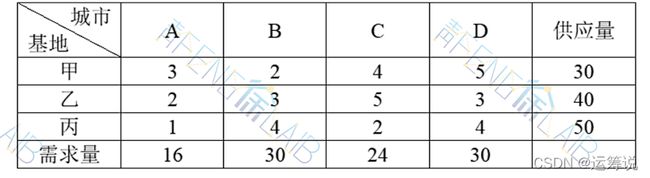
有三个牧业基地向4个城市提供鲜奶,4个城市每日的鲜奶需求量、3个基地的每日鲜奶供应量以及运送每千升鲜奶的费用如下表所示,试确定最经济的鲜奶运输方案。
2.问题解析
总供应量=30+40+50=120
总需求量=16+30+24+30=100
供过于求,即产量大于销量,这是一个产大于销的运输问题。要将问题转化为产销平衡的运输问题,需进行以下几个方面的调整。
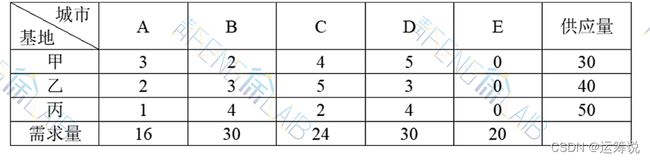
(1)增加一个虚拟销地E,使其总需求量为120-100=20。
(2)由于销地是虚拟的,实际上是产量过剩的物资在产地就地储存,所以不会产生实际的运输,即不会产生运费。
因此新的供需量及单位运价表如下所示。
3.问题求解
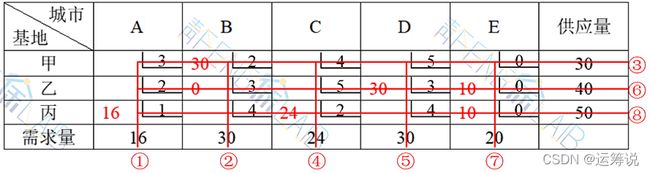
(1)运用最小元素法确定初始方案,如下表所示。
易错点:线②和③同时划,出现退化现象,此时应该补一个值为0的基解。
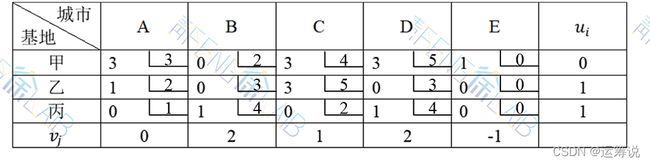
(2)运用位势法对上述运输方案进行检验,检验数表如下。
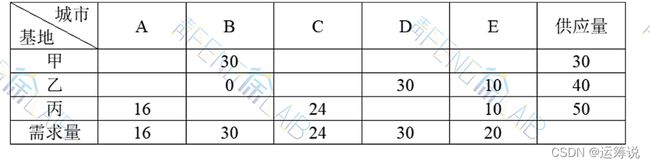
因为所有非基变量的检验数都大于等于0,则当前方案是最优方案,最优方案如下表所示。
#3产小于销的运输问题
1.问题描述
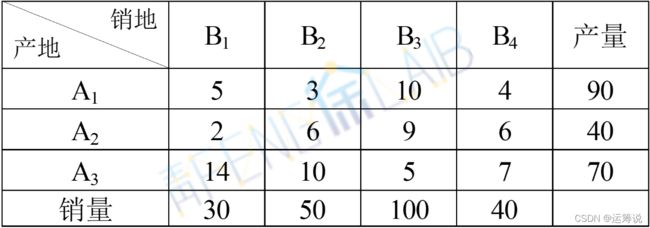
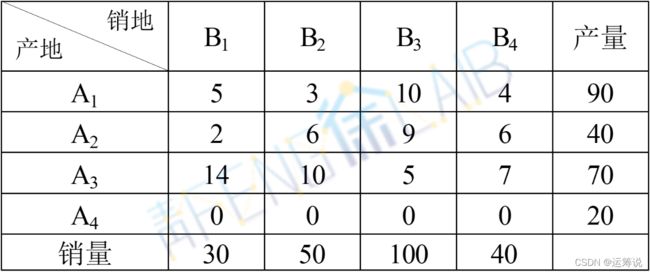
某三个煤炭厂供应4个地区,假定等量的煤炭在这些地区使用效果相同,已知各煤炭厂年产量,各地区的需要量及从各煤炭厂到各地区的单位运价表如下所示,试决定最优的调运方案。
2.问题解析
总产量=90+40+70=200
总销量=30+50+100+40=220
产量小于销量,即这是一个产小于销的运输问题。要将问题转化为产销平衡的运输问题,需进行以下几个方面的调整。
(1)增加一个虚拟产地,使其总产地为220-200=20。
(2)由于产地是虚拟的,所以不会产生实际的运输,也就不会产生运费。
因此新的供需量及单位运价表如下所示。
3.问题求解
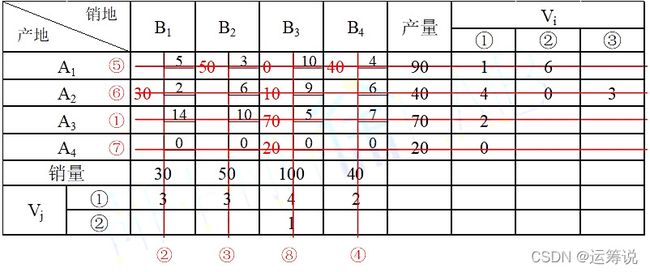
(1)运用伏格尔法确定初始可行解。
易错点:线④和⑤同时划,出现退化现象,此时应该补一个值为0的基解。
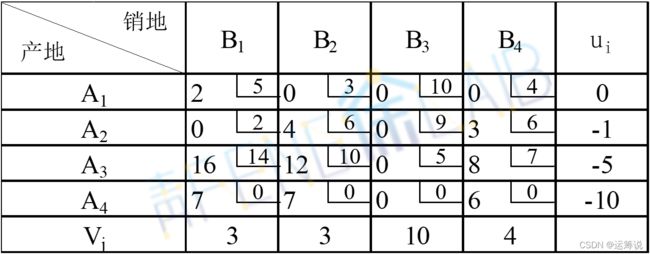
(2)运用位势法对上述运输方案进行检验,检验数表如下。
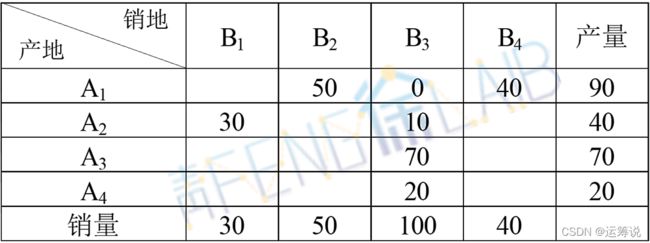
因为检验数都大于等于0,则当前方案是最优方案,最优方案如下表所示。
#4弹性需求的运输问题
1.问题描述
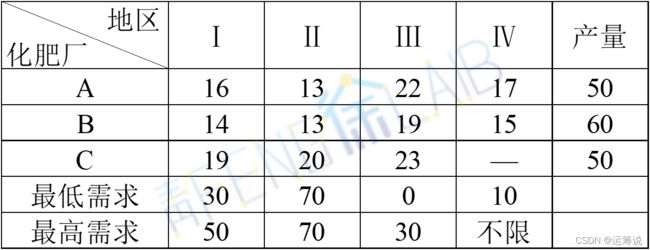
设有三个化肥厂供应四个地区的农用化肥,假定等量的化肥在这些地区使用效果相同,已知各化肥厂年产量,各地区的需要量及从各化肥厂到各地区的单位运价表如下所示,试决定总运费最少的调运方案。
2.问题解析
地区Ⅳ的最高需求是当其他地区最低需求被满足时,供给给产地Ⅳ的数量。
地区Ⅳ的最高需求=50+60+50-30-70=60
总产量=50+60+50=160
最低需求=30+70+10=110
最高需求=50+70+30+(160-30-70)=310
这是一个具有需求弹性的运输问题,要将问题转化为产销平衡问题进行求解,需进行以下几个方面的调整。
(1)将地区划分为刚性需求地区和弹性需求地区,刚性需求地区要满足该地区的最低需求,弹性需求地区需要满足弹性需求,运价不变。
(2)增加一个虚拟化肥厂D,使其产销平衡。
(3)刚性需求地区的需求必须满足因此,虚拟化肥厂不能向刚性需求地区运输花费,即设虚拟化肥厂到刚性需求地区的运费为无限大的M。
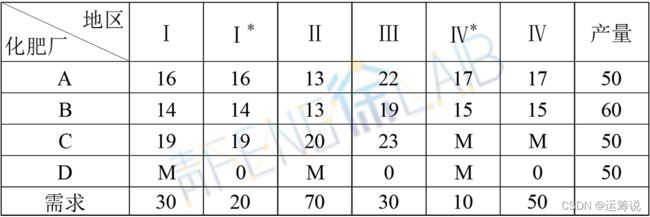
因此新的产销量及单位运价表如下所示。
3.问题求解
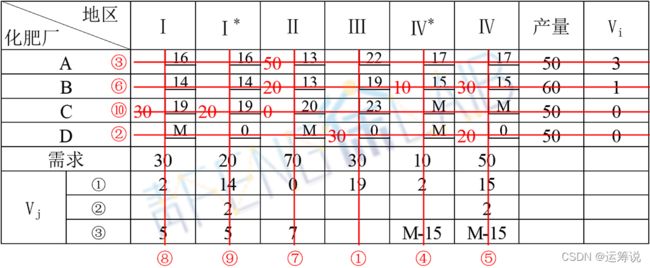
(1)运用伏格尔法确定初始可行解。
易错点:线⑥和⑦同时划,出现退化现象,此时应该补一个值为0的基解。
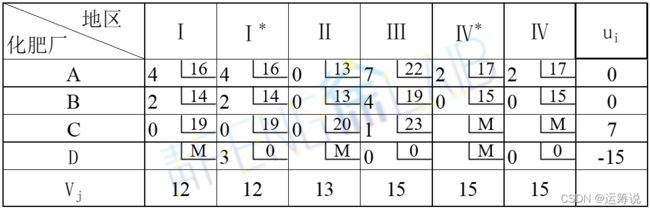
(2)运用位势法对上述运输方案进行检验,检验数表如下。
因为所有非基变量的检验数都大于等于0,则当前方案是最优方案,最优方案如下表所示。
#5中间转运的运输问题
1.问题描述
某糖果公司下设三个工厂,每日产量分别为:A1—7吨、A2—4吨、A3—9吨。该公司将这些产品运往四个门市部,各门市部每日销量为:B1—3吨、B2—6吨、B3—5吨、B4—6吨。
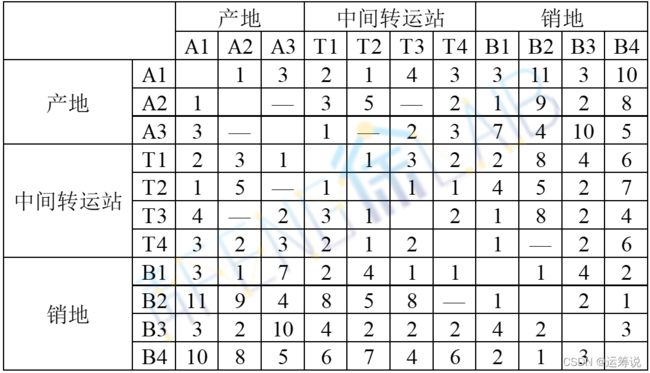
假定:①每个工厂生产的糖果不一定直接发送到销售点,可以将其中几个产地的糖果集中一起运;②运往各销地的糖果可以先运给其中几个销地,再转运给其他销地;③除产、销地之外,中间还有几个转运站,在产地之间、销地之间或产销地之间转运。已知各产地、销地、中间转运站及相互之间每吨糖果的运价如下表,问在考虑到产销地之间直接运输和非直接运输的各种可能方案的情况下,如何将三个厂每天生产的糖果运往销售地,使总的运费最少?
2.问题解析
这是一个具有中转运输的运输问题,要将问题转化为产销平衡问题进行求解,需进行以下几个方面的调整。
(1)由于问题中所有产地、中间转运站、销地都可以看作产地,又可以看作销地。因此把整个问题当作有11个产地和11个销地的扩大的运输问题。
(2)对扩大的运输问题建立单位运价表,方法是将不可能的运输方案运价用任意大的正数M代替。
(3)所有中间转运站的产量等于销量,由于运费最少时不可能出现一批物资来回倒运的现象,所以每个转运站的运数不超过20。可以规定中间转运站的产销量均为20,由于实际转运量不超过各自的产量和销量,所以在每个约束条件中增加一个松弛变量xi,相当于自己运给自己,对应运价为0。
(4)扩大的运输问题中原来的产地与销地因为也起中间转运站的作用,所以,同样在原来的产量与销量的数字上加20,即三个糖果厂产量改为27、24、29,销量均为20;四个销售点销量改为23、26、25、26,产量均为20,同时引进xii作为松弛变量。
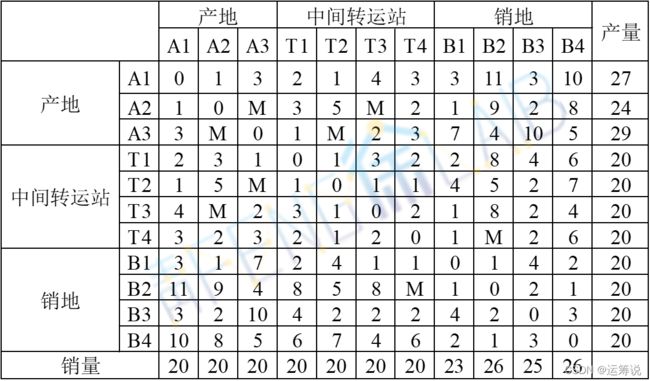
因此新的产销量及单位运价表如下所示。
3.问题求解
应用LINDO软件求解,最优方案如下表所示。
以上就是本节运输问题案例的全部内容啦,通过对这一节的学习,大家是否掌握了运输问题的各种形式和表上作业法呢?动动小手做一做,收获会有大不同哦!
END
运筹说
作者|何洋洋 裴传涛 陈志昂
责编|何洋洋
审核|徐小峰
· 知乎|运筹说 ·
· Bilibili|运筹说 ·
· CSDN|运筹说 ·