第八十六篇 K-means(聚类) 和 KNN(分类) 算法
心得: 每天坚持学一点,新的算法新的技能,学到的都是属于自己的,希望在这里记录一下自己的历程,不忘初心
机器学习分为四大块算法
1. classification (分类)
给定一个样本特征 , 我们希望预测其对应的属性值 , 如果 是离散的, 那么这就是一个分类问题,反之,如果 是连续的实数, 这就是一个回归问题。
类问题最常用的学习算法包括 SVM (支持向量机) , SGD (随机梯度下降算法), Bayes (贝叶斯估计), Ensemble(集成), KNN 等
2. regression (回归)
无论是分类还是回归,都是想建立一个预测模型 ,给定一个输入 , 可以得到一个输出;不同的只是在分类问题中,预测结果是离散的; 而在回归问题中预测结果是连续的
回归问题也能使用 SVR, SGD, Ensemble 等算法,以及其它线性回归算法。
3. clustering (聚类)
给定一组样本特征 , 我们没有对应的属性值 , 而是想发掘这组样本在多维空间的分布, 比如分析哪些样本靠的更近,哪些样本之间离得很远, 这就是属于聚类问题
clustering 事先不知道样本的属性范围,只能凭借样本在特征空间的分布来分析样本的属性。这种问题一般更复杂。而常用的算法包括 k-means (K-均值), GMM (高斯混合模型) 等。
4. dimensionality reduction (降维)
如果我们想用维数更低的子空间来表示原来高维的特征空间, 那么这就是降维问题。
特征的维数过高, 会增加训练的负担与存储空间, 降维就是希望去除特征的冗余, 用更加少的维数来表示特征.降维算法最基础的就是PCA了, 后面的很多算法都是以PCA为基础演化而来。
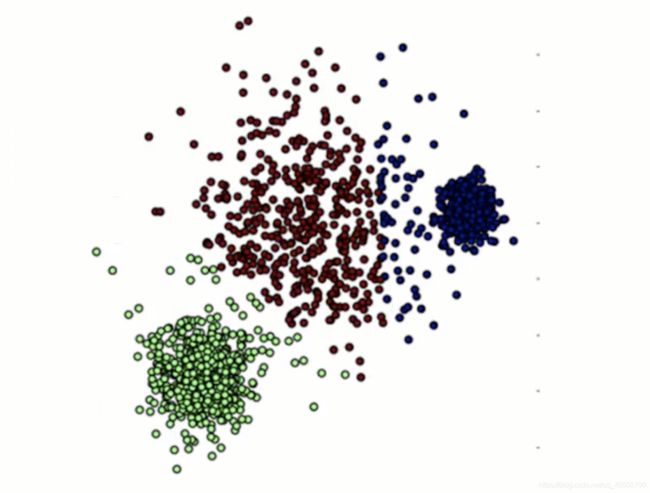
一、K-means算法(聚类)(无监督学习)
1. 原理:
它是很典型的基于距离的聚类算法,采用距离作为相似性的评价指标,即认为两个对象的距离越近,其相似度就越大。它是使用欧氏距离度量的(简单理解就是两点间直线距离,欧氏距离只是将这个距离定义更加规范化,扩展到N维而已)。它可以处理大数据集,且高效。聚类结果是划分为k类的k个数据集。
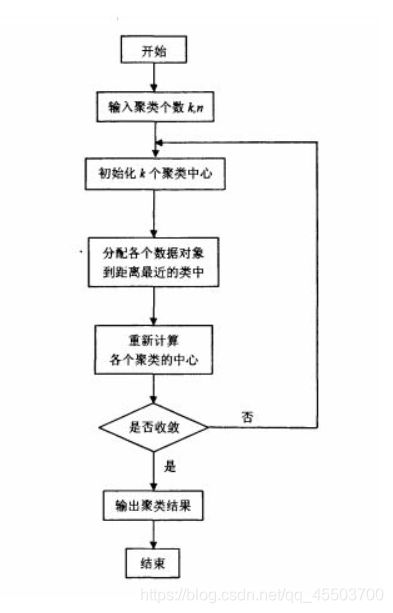
2. 训练过程
- 指定k个质心,随机选择质心的位置
- 计算所有样本到每个质心的距离,选择出此样本距离那个质心最近的距离,就将此样本划分到此簇内
- 对每一个簇,计算所有点的均值并将均值作为质心;继续迭代计算,直至质心不再发生变化
3. 算法难点
-
聚类中心的个数K 需要事先给定,但在实际中这个 K 值的选定是非常难以估计的,很多时候,事先并不知道给定的数据集应该分成多少个类别才最合适
-
初始点的位置选取
首先随机选择一个点作为第一个初始类簇中心点,然后选择距离该点最远的那个点作为第二个初始类簇中心点,然后再选择距离前两个点的最近距离最大的点作为第三个初始类簇的中心点,以此类推,直至选出K个初始类簇中心点。
K-mean算法代码 :http://rosettacode.org/wiki/K-means%2B%2B_clustering#Python
二、KNN算法(分类)(监督学习)
1. 原理
KNN算法也叫做K近邻算法,用一句话可以来描述此算法的原理,那就是:近朱者赤,近墨者黑
它属于lazy learning。即它没有明显的前期训练过程,而是程序开始运行时,把数据集加载到内存后,不需要进行训练,就可以开始分类了。 K N N也是一种监督学习算法,通过计算新数据与训练数据特征值之间的距离,然后选取K(K>=1)个距离最近的邻居进行分类判(投票法)或者回归。若K=1,新数据被简单分配给其近邻的类。
2. 算法训练预测过程

上图中,所有样本可以使用一个二维向量表征。图中,蓝色方形样本和红色三角形样本为已知分类样本。若使用KNN对图中绿色圆形未知分类样本进行分类,当K=3时,其三近邻中有2个红色三角形样本和1个蓝色方形样本,因此预测该待分类样本为红色三角形样本;当K=5时,其三近邻中有3个红色三角形样本和2个蓝色方形样本,因此预测该待分类样本为蓝色方形样本;
步骤
1)计算测试数据与各个训练数据之间的距离;可以使用欧式距离的公式来进行计算。
2)按照距离的递增关系进行排序;
3)选取距离最小的K个点(k值是由自己来确定的)
4)确定前K个点所在类别的出现频率;
5)返回前K个点中出现频率最高的类别作为测试数据的预测分类。
3. 算法参数选取
K值的选取:K是一个自定义的常量,是KNN算法中一个非常重要的参数。K值的选取会影响待分类样本的分类结果,会影响算法的偏差与方差。
偏差:模型输出值与真实值之间的差异。偏差越高,则数据越容易欠拟合(Underfitting),未能充分利用数据中的有效信息。
K值较小:就相当于用较小的领域中的训练实例进行预测,“学习”近似误差会减小, K值的减小就意味着整体模型变得复杂,容易发生过拟合,即增大了方差;
K值较大:就相当于用较大领域中的训练实例进行预测,其优点是可以减少学习的估计误差,但缺点是学习的近似误差会增大。这时候,与输入实例较远(不相似的)训练实例也会对预测器作用,使预测发生错误,且K值的增大就意味着整体的模型变得简单。k很大,那么可以减少干扰数据的影响,但是此时就导致了系统性偏差(K值太小会造成过度拟合),比如如果取k为总的训练数据数,那么每次投票肯定都是训练数据中多的类别胜利。显然训练数据的系统性偏差会影响结果。
通常情况下,我们需要对 k 经过多种尝试,来决定到底使用多大的 k 来作为最终参数。k通常会在3~10直接取值,或者是k等于训练数据的平方根。比如15个数据,可能会取k=4。在实际应用中,一般采用交叉验证法(简单来说,就是一部分样本做训练集,一部分做测试集)来选择最优的K值。
sklearn-knn代码示例:
在使用KNN算法之前,我们要先决定K的值是多少,要选出最优的K值,可以使用sklearn中的交叉验证方法,代码如下:
from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
#读取鸢尾花数据集
iris = load_iris()
x = iris.data
y = iris.target
k_range = range(1, 31)
k_error = []
#循环,取k=1到k=31,查看误差效果
for k in k_range:
knn = KNeighborsClassifier(n_neighbors=k)
#cv参数决定数据集划分比例,这里是按照5:1划分训练集和测试集
scores = cross_val_score(knn, x, y, cv=6, scoring='accuracy')
k_error.append(1 - scores.mean())
#画图,x轴为k值,y值为误差值
plt.plot(k_range, k_error)
plt.xlabel('Value of K for KNN')
plt.ylabel('Error')
plt.show()
k在11的时候效果最好
import matplotlib.pyplot as plt
from numpy import *
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets
import numpy as np
n_neighbors = 11
# 导入一些要玩的数据
iris = datasets.load_iris()
x = iris.data[:, :2] # 我们只采用前两个feature,方便画图在二维平面显示
y = iris.target
h = .02 # 网格中的步长
# 创建彩色的图
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
#weights是KNN模型中的一个参数,上述参数介绍中有介绍,这里绘制两种权重参数下KNN的效果图
for weights in ['uniform', 'distance']:
# 创建了一个knn分类器的实例,并拟合数据。
clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)
clf.fit(x, y)
# 绘制决策边界。为此,我们将为每个分配一个颜色
# 来绘制网格中的点 [x_min, x_max]x[y_min, y_max].
x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# 将结果放入一个彩色图中
Z = Z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
# 绘制训练点
plt.scatter(x[:, 0], x[:, 1], c=y, cmap=cmap_bold)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("3-Class classification (k = %i, weights = '%s')"
% (n_neighbors, weights))
plt.show()