拉格朗日松弛(一)——理论及算法
目录
- 背景
- 拉格朗日松弛——理论
- 拉格朗日松弛——算法
-
- 次梯度优化算法
- 拉格朗日松弛启发式算法
- 参考资料
背景
Marshall L.Fisher在1981年发表在《Management Science》上的《The Lagrangian Relaxation Method for Solving Integer Programming Problems》1在2004年被评为“《Management Science》首个50年中十大最具影响力的主题之一”。
在中国知网中,以“拉格朗日松弛”作为关键词在“篇关摘”选项下检索,并对结果进行计量可视化分析可得到如下的图表。
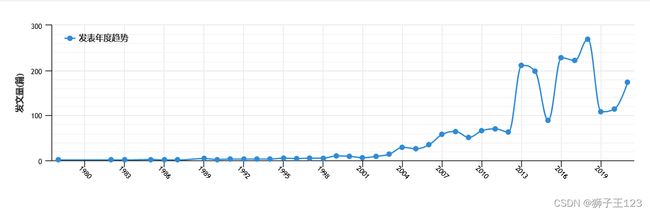 从发文量这一指标可以看到,近10年涉及这一方法的论文显著增多。
从发文量这一指标可以看到,近10年涉及这一方法的论文显著增多。
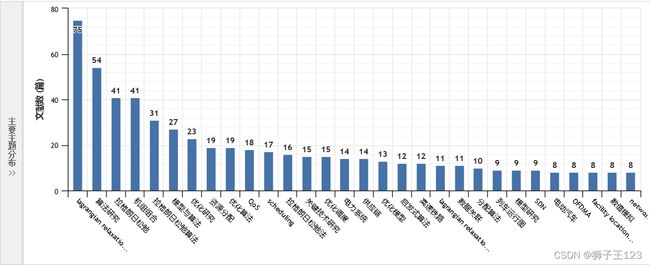
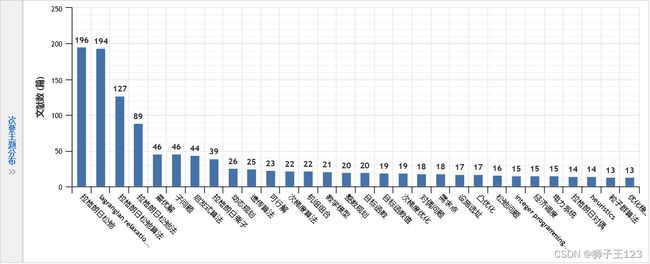
从主要主题分布、次要主题分布中可以看到,在理论层面,该方法与动态规划、整数规划、凸优化和启发式算法等知识都有较为紧密的联系。在应用层面,该方法在机组组合、资源分配、调度、供应链和设施选址等领域都有应用。
拉格朗日松弛——理论
理论和算法部分内容参考资料2进行介绍,主要介绍拉格朗日松弛的思想、重要结论和拉格朗日松弛算法,结论的证明和更多内容可参考该书。除此之外,本文也吸纳了网上其他相关资料,帮助读者理解。
松弛的意思即为放松约束,对于一个标准化为求最小值的优化问题,放松约束会使得有可能得到目标函数值更小的解,换言之,松弛可以求得原问题的一个下界,这为评价其他算法的有效性提供了一种途径,也为原问题的求解提供了更多信息。
该方法常用在整数规划和混合整数规划中。
松弛方法主要有以下四种:线性规划松弛(将整数约束松弛至实数约束)、对偶规划松弛(求解对偶规划,根据弱对偶定理,求 max \text{max} max 的对偶问题提供了求 min \text{min} min 的原问题的一个下界)、代理松弛(通过组合多个约束减少约束的数量,如相加)和拉格朗日松弛。本篇博文介绍拉格朗日松弛。
拉格朗日松弛方法的基本原理:将造成问题难的约束吸收到目标函数中,并使得目标函数仍保持线性,使得变换后的问题可以在多项式时间求解或者尽管不能在多项式时间求解但由于规模较小而可以快速求解3,从而为原问题的求解提供帮助。

如上图4所示(细线红框中应为 “ ≥ \ge ≥” 和 “ ≤ \le ≤” ,粗线红框中应为“lower”,“lower bound”表示下界),假设一个问题的约束可以分为两部分,即图中的 A A A 和 D D D( D 1 D_1 D1、 D 2 D_2 D2、 D 3 D_3 D3),它们的区别是 D D D 只和某一部分变量有关,而 A A A 和所有变量都有关,则 A A A 就是上面所说的“造成问题难的约束”(也称复杂约束)。拉格朗日松弛就是将这个复杂约束放到了目标函数中。关于 λ \lambda λ 为什么要求非负,可参见5。下图6可以帮助理解。

进一步地,已知拉格朗日松弛后的目标函数值 z L R z_{LR} zLR 是原问题目标函数值 z z z 的一个下界,由于需要尽可能地接近原问题的目标函数值,故可以对松弛后的问题 z L R z_{LR} zLR 关于 λ λ λ 求最大值(构成对偶问题,Dual Problem),得到的是所有下界中的最佳值 z L D z_{LD} zLD(下图4红框中应为 z L D z_{LD} zLD )。

拉格朗日松弛的用途如下6。

以上是拉格朗日松弛的基础理论,下面介绍一些常见的变形。
首先是等式约束的松弛。这里和“线性规划对偶问题中等式约束对应的对偶变量没有符号限制”以及“库恩-塔克条件(KKT条件)中等式约束对应的系数没有符号限制”的原理完全相同,等式约束松弛对应的系数也没有符号限制(两个非负的系数相减得到一个没有符号限制的系数)。
其次是拉格朗日分解。回顾上述问题4,不妨设 n = 3 n=3 n=3 ,与下面的示意图保持一致。

则将松弛后的问题目标函数中的 x x x 按照 x 1 x_1 x1、 x 2 x_2 x2 和 x 3 x_3 x3 分解可以等价变换为如下的问题。
z L R ( λ ) = minimize c 1 T x 1 + c 2 T x 2 + c 3 T x 3 + λ T ( A 1 x 1 + A 2 x 2 + A 3 x 3 − b ) subject to D 1 T x 1 ≤ e 1 D 2 T x 2 ≤ e 2 D 3 T x 3 ≤ e 3 x 1 , x 2 , x 3 ∈ Z + n \begin{array}{ll} z_{LR}(\lambda)=\text{minimize} & c_1^T x_1 +c_2^T x_2+c_3^T x_3+\lambda^T(A_1x_1+A_2x_2+A_3x_3-b) \\ \text{subject to} & D_1^T x_1 \le e_1 \\ & D_2^T x_2 \le e_2 \\ & D_3^T x_3 \le e_3 \\ & x_1, x_2, x_3 \in \Bbb{Z^n_+} \end{array} zLR(λ)=minimizesubject toc1Tx1+c2Tx2+c3Tx3+λT(A1x1+A2x2+A3x3−b)D1Tx1≤e1D2Tx2≤e2D3Tx3≤e3x1,x2,x3∈Z+n进一步可将上述问题按照按照 x 1 x_1 x1、 x 2 x_2 x2 和 x 3 x_3 x3 分解为三个子问题,由于目标函数和约束都是关于 x 1 x_1 x1、 x 2 x_2 x2 和 x 3 x_3 x3 可分的,故这一步是等价变换。
子问题一:
z L R 1 ( λ ) = minimize c 1 T x 1 + λ T ( A 1 x 1 − b ) subject to D 1 T x 1 ≤ e 1 x 1 ∈ Z + n \begin{array}{ll} z_{LR1}(\lambda)=\text{minimize} & c_1^T x_1+\lambda^T(A_1x_1-b) \\ \text{subject to} & D_1^T x_1 \le e_1 \\ & x _1\in \Bbb{Z^n_+} \end{array} zLR1(λ)=minimizesubject toc1Tx1+λT(A1x1−b)D1Tx1≤e1x1∈Z+n子问题二:
z L R 2 ( λ ) = minimize c 2 T x 2 + λ T A 2 x 2 subject to D 2 T x 2 ≤ e 2 x 2 ∈ Z + n \begin{array}{ll} z_{LR2}(\lambda)=\text{minimize} & c_2^T x_2+\lambda^TA_2x_2 \\ \text{subject to} & D_2^T x_2 \le e_2 \\ & x _2\in \Bbb{Z^n_+} \end{array} zLR2(λ)=minimizesubject toc2Tx2+λTA2x2D2Tx2≤e2x2∈Z+n子问题三:
z L R 3 ( λ ) = minimize c 3 T x 3 + λ T A 3 x 3 subject to D 3 T x 3 ≤ e 3 x 3 ∈ Z + n \begin{array}{ll} z_{LR3}(\lambda)=\text{minimize} & c_3^T x_3+\lambda^TA_3x_3 \\ \text{subject to} & D_3^T x_3 \le e_3 \\ & x _3\in \Bbb{Z^n_+} \end{array} zLR3(λ)=minimizesubject toc3Tx3+λTA3x3D3Tx3≤e3x3∈Z+n分解后的子问题的目标函数值和原问题目标函数值有如下的关系。
z L R 1 ( λ ) + z L R 2 ( λ ) + z L R 3 ( λ ) = z L R ( λ ) ≤ z z_{LR1}(\lambda)+z_{LR2}(\lambda)+z_{LR3}(\lambda)=z_{LR}(\lambda) \le z zLR1(λ)+zLR2(λ)+zLR3(λ)=zLR(λ)≤z对偶问题如下。
z L D = max z L R 1 ( λ ) + z L R 2 ( λ ) + z L R 3 ( λ ) z_{LD}= \text{max}\space z_{LR1}(\lambda)+z_{LR2}(\lambda)+z_{LR3}(\lambda) zLD=max zLR1(λ)+zLR2(λ)+zLR3(λ)可以看到,在拉格朗日松弛的基础上,拉格朗日分解将原问题拆分为了不含复杂约束的子问题,从而可以通过求解较易的子问题来对原问题进行近似。
拉格朗日松弛——算法
拉格朗日松弛算法包含两部分内容:一方面是提供原问题的下界(求解 z L D z_{LD} zLD),另一方面则演变为拉格朗日松弛启发式算法。
次梯度优化算法
次梯度(subgradient)与梯度(gradient)十分相似,次梯度是函数在某些点处不可微时对梯度的一种扩展。引入次梯度是因为 z L R ( λ ) z_{LR}(\lambda) zLR(λ) 是一个关于 λ \lambda λ 的分段线性函数,这一点将在后续说明。
按照2中的编号介绍相关定义和定理如下,详细证明可参看之。
定义 7.4.1 函数 g : R m → R g:\Bbb{R^m}\to\Bbb{R} g:Rm→R 满足 g ( α x 1 + ( 1 − α ) x 2 ) ≥ α g ( x 1 ) + ( 1 − α ) g ( x 2 ) , ∀ x 1 , x 2 ∈ R m , 0 ≤ α ≤ 1 \begin{array}{ll} g(\alpha x^1+(1-\alpha)x^2)\ge\alpha g(x^1)+(1-\alpha)g(x^2) , \forall x^1, x^2\in \Bbb{R^m}, 0 \le \alpha \le1 \end{array} g(αx1+(1−α)x2)≥αg(x1)+(1−α)g(x2),∀x1,x2∈Rm,0≤α≤1则称 g ( x ) g(x) g(x) 为凹函数。
定理 7.4.1 若经拉格朗日松弛后的问题( z L R z_{LR} zLR)的可行解集合 Q Q Q 是有限个整数点的集合,则目标函数 z L R ( λ ) = min c T x + λ T ( A x − b ) \begin{array}{ll} z_{LR}(\lambda)=\text{min}\space c^T x+\lambda^T(Ax-b) \end{array} zLR(λ)=min cTx+λT(Ax−b)是凹函数。(通过定义证明)
定理 7.4.2 可微函数 g ( x ) g(x) g(x) 是凹函数的充分必要条件为 ∀ x ∗ ∈ R m \forall x^*\in\Bbb{R^m} ∀x∗∈Rm,存在 s = ( s 1 , s 2 , … , s m ) T ∈ R m s=(s_1,s_2,…,s_m)^T\in\Bbb{R^m} s=(s1,s2,…,sm)T∈Rm使得 g ( x ∗ ) + s T ( x − x ∗ ) ≥ g ( x ) , ∀ x ∈ R m . \begin{array}{ll} g(x^*)+s^T(x-x^*)\ge g(x), \forall x\in\Bbb{R^m}. \end{array} g(x∗)+sT(x−x∗)≥g(x),∀x∈Rm.(类比凸函数的一阶条件理解)
下图1是定理 7.4.1结论的示意图(图中的 u u u 即为 λ \lambda λ ),随着 λ \lambda λ 的变化, z L R ( λ ) z_{LR}(\lambda) zLR(λ) 在不同的点 x x x( x 1 x^1 x1、 x 2 x^2 x2、 x 3 x^3 x3、 x 4 x^4 x4)处达到最小值,而当 x x x 不变时, z L R ( λ ) z_{LR}(\lambda) zLR(λ) 关于 λ \lambda λ 是一线性函数,故总结来看 z L R ( λ ) z_{LR}(\lambda) zLR(λ) 关于 λ \lambda λ 是一分段线性函数,亦是凹函数。每段直线表示取最小值的 x x x 点保持不变。
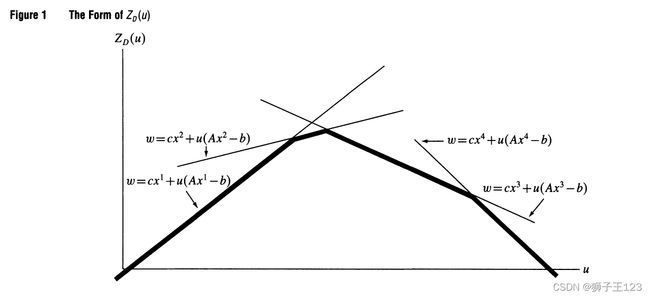
定义 7.4.2 若函数 g : R m → R g:\Bbb{R^m}\to\Bbb{R} g:Rm→R 为凹函数,且在点 x ∗ ∈ R m x^*\in\Bbb{R^m} x∗∈Rm 处,向量 s ∈ R m s\in\Bbb{R^m} s∈Rm 满足 g ( x ∗ ) + s T ( x − x ∗ ) ≥ g ( x ) , ∀ x ∈ R m \begin{array}{ll} g(x^*)+s^T(x-x^*)\ge g(x) , \forall x\in \Bbb{R^m} \end{array} g(x∗)+sT(x−x∗)≥g(x),∀x∈Rm则称 s ∈ R m s\in\Bbb{R^m} s∈Rm 为函数 g ( x ) g(x) g(x) 在 x ∗ x^* x∗处的一个次梯度。 g ( x ) g(x) g(x) 在 x ∗ x^* x∗ 处的所有次梯度组成的集合记为 ∂ g ( x ∗ ) \partial g(x^*) ∂g(x∗)。(直观理解,在一元函数的情况下,次梯度可以是函数在 x ∗ x^* x∗ 处左导数和右导数之间的任何一个值。)
定理 7.4.3 若 g ( x ) g(x) g(x) 为凹函数, x ∗ x^* x∗ 为 max { g ( x ) ∣ x ∈ R m } \text{max}\space\{g(x)|x\in\ \Bbb{R^m}\} max {g(x)∣x∈ Rm} 最优解的充分必要条件为 0 ∈ ∂ g ( x ∗ ) 0\in\partial g(x^*) 0∈∂g(x∗)。
次梯度优化算法
- STEP1:任选一个初始拉格朗日乘子 λ 1 \lambda^1 λ1,并置 t = 1 t=1 t=1.
- STEP2:针对本次迭代的 λ t \lambda^t λt,求解对偶问题内层的最小化问题,并从 ∂ z L R ( λ t ) \partial z_{LR}(\lambda^t) ∂zLR(λt) 中任选一个次梯度 s t s^t st;若 s t = 0 s^t=0 st=0,则 λ t \lambda^t λt 达到最优解而停止计算;否则 λ t + 1 = max { λ t + θ t s t , 0 } \lambda^{t+1}=\text{max}\space\{\lambda^{t}+\theta_ts^t, 0 \} λt+1=max {λt+θtst,0},置 t = t + 1 t=t+1 t=t+1, 重复STEP2。
实际应用中不可能迭代无穷多次,故必须给出 θ t \theta_t θt 的确定方法和算法停止的条件。
- θ t \theta_t θt 的确定方法
实际计算的目的是尽快得到一个可以接受的下界,故常采用启发式的方法进行确定。主要有以下两类方法。
第一类方法是使 θ t \theta_t θt 以指数速度下降,迭代次数较少。更新公式如下。
θ t = θ 0 ρ t , 0 < ρ < 1 \theta_t=\theta_0\rho^t, 0\lt\rho\lt1 θt=θ0ρt,0<ρ<1第二类方法的主要思想是用对偶问题的上下界的差修正 θ t \theta_t θt 变化的速度。更新公式如下。
θ t = z U P ( t ) − z L B ( t ) ∣ ∣ s t ∣ ∣ 2 β t \theta_t=\frac{z_{UP}(t)-z_{LB}(t)}{||s^t||^2}\beta_t θt=∣∣st∣∣2zUP(t)−zLB(t)βt式中 0 ≤ β t ≤ 2 0\le\beta_t\le2 0≤βt≤2,一般取 β 0 = 2 \beta_0=2 β0=2。当 z L R ( λ ) z_{LR}(\lambda) zLR(λ) 上升时, β t \beta_t βt 不变,当 z L R ( λ ) z_{LR}(\lambda) zLR(λ) 在给定的若干步没有变化时,则 β t \beta_t βt 减半。 z U P ( t ) z_{UP}(t) zUP(t) 为原问题最优目标值的一个上界(从而也是对偶问题的上界),可以用一个可行解确定,或者估计得到。 z U P ( t ) z_{UP}(t) zUP(t) 可随 t t t 的变化而逐步修正。 z L B ( t ) z_{LB}(t) zLB(t) 是 z L R ( λ t ) z_{LR}(\lambda^t) zLR(λt) 的一个下界,一般取 z L B ( t ) = z L R ( λ t ) z_{LB}(t)=z_{LR}(\lambda^t) zLB(t)=zLR(λt),有时为了计算简单只取一个固定值。 - 算法停止的条件
算法停止的条件主要有以下四种。
第一种是迭代次数不超过 T T T。这是一种最为简单的原则,很容易控制计算的复杂性,但解的质量无法保证。
第二种是 ∣ ∣ s t ∣ ∣ ≤ ϵ ||s^t||\le\epsilon ∣∣st∣∣≤ϵ( ϵ \epsilon ϵ为一较小的正数),这是对理想状态 s t = 0 s^t=0 st=0 的一种近似。
第三种是 z U P ( t ) = z L B ( t ) z_{UP}(t)=z_{LB}(t) zUP(t)=zLB(t),此时表明已经找到原问题的最优解,有 z = z U P ( t ) = z L B ( t ) z=z_{UP}(t)=z_{LB}(t) z=zUP(t)=zLB(t)。
第四种是 λ t \lambda^t λt 或 z L R ( λ t ) z_{LR}(\lambda^t) zLR(λt) 在规定的步数内变化不超过一个给定的值,这时可认为目标值不会再变化,因此停止计算。
具体应用中,可以采用以上停止条件之一,也可以综合运用。
拉格朗日松弛启发式算法
上述提到的内容中有这样一个结论4(红框中应为 z L D z_{LD} zLD):对比左边的原问题和右边的对偶问题可以发现,求解对偶问题时可行域有所扩大,因此我们在求解对偶问题时得到的较优的解(由次梯度优化算法给出)可能并不是原问题的可行解,此时通常根据问题的特点采用启发式的方法将该解修正为原问题的可行解,整个过程构成了拉格朗日松弛启发式算法。

参考资料
Fisher, M.L. 1981. The Lagrangian Relaxation Method for Solving Integer Programming Problems. Management Science. 27(1) 1-18. ↩︎ ↩︎
邢文训, 谢金星. 现代优化计算方法(第2版)[M].清华大学出版社, 2005:210-242. ↩︎ ↩︎
王源. 拉格朗日松弛求解整数规划浅析(附Python代码实例) ↩︎
TransNET. 拉格朗日松弛问题 ↩︎ ↩︎ ↩︎ ↩︎
想问个问题,为什么拉格朗日乘数法的乘子要大于0? ↩︎
拉格朗日松弛 PPT ↩︎ ↩︎