PaperNotes(15)-图神经网络、PyG极简版入门笔记

一文读懂图卷积GCN(https://zhuanlan.zhihu.com/p/89503068)读书笔记
本文更强调的是空域卷积，比较简单的介绍。

1.GNN,GCN,GE的区别

Graph Embedding：表示学习的范畴，将图中节点/将整个图表示为低维、实值、稠密的向量。（可以将用户表示成向量的形式，再勇于节点分类任务）图嵌入的方式有三种：矩阵分解，deepWalk, 图神经网络

Graph Neural Netvork：神经网络在图上应用的模型统称。依据传播的方式不同，可以分为图卷积神经网络，图注意力网络，图LSTM。(本质还是将网络结构技巧借鉴过来做新的尝试)。

Graph Convolutional Network：采用卷积操作图神经网络，是最经典的图神经网络。引发了无数的改进工作。

一句话概括三者的关系：GCN是一类GNN，GNN可以实现GE。

现实需求：现实中，像图像一样排列整齐的数据只占很小的一部分，还有更大的一部分数据以图的形式存储（社交网络的信息，知识图谱，蛋白质网络，万维度网）
提出疑问：能够类似于图像领域的卷积操作一样，具有一个通用的范式来抽取图像特征呢？–图卷积(处理非结构化数据的利器)

2.图卷积的通式–矩阵该如何作用

图的表示:
图$G=(V,E)$，其中$V$为节点的集合，$E$为边的集合。对于每个节点i，均有特征向量$x_i$，可以用矩阵$X_{N\ast D}$表示。
图相关矩阵：(Laplacian矩阵的定义是否有具体含义？)
度矩阵D-对角阵，对角线元素为各个结点的度，无向图：与该顶点相关联的边数；有向图：入度和出度
邻接矩阵A：表示结点间关系，无向图：对称矩阵，有边即为1；有向图：有向连接才为1。
Laplacian 矩阵L：L=D-A

图卷积核心思想：每个节点受到邻居节点的影响，通式：
$$H^{l+1}=f(H^l,A)$$

其中：$H^0=X$为图的特征矩阵，$f$的差异定义了不同算法的差异。

2.1实现1

$$H^{l+1}=\sigma (A{H}^l{W}^l)$$

出发点：结点特征与邻居结点的特征有关，邻居结点各个维度特征的加权和。多层叠加后能够利用多层邻居的信息。

存在的问题：没有考虑结点对自身的影响；A没有被规范化时，邻居结点多的结点拥有更大的影响力。

2.2实现2

$$H^{l+1}=\sigma (L{H}^l{W}^l)$$
使用Laplacian 矩阵（Combinatorial Laplacian​），对角线未知非零；解决了没有考虑自身结点信息自传递的问题。

2.3实现3

利用Symmetric normalized Laplacian同时解决两个问题：自传递和归一化的问题。

归一化的Laplacian矩阵具有多种形式，这些矩阵其实就是对应的图卷积核。

3.PyTorch geometric

PyTorch geometric–基于PyTorch的用于处理不规则数据（图）的库，能够用于快速实现图等数据的表征学习的框架。
PyG-document

对机器学习库最关心的内容：数据规范，模型定义，参数学习，模型测试

3.1 PyG内置数据集

PyTorch Geometric 包含了很多常见的基本数据集，例如：Cora, Citeseer, Pubmed

3.1.1ENZYMES dataset

graph-level数据集载入demo–ENZYMES dataset, 包含6大类，一共60个图，能够用于graph-level的分类任务。

from torch_geometric.datasets import TUDataset
# graph_level demo
dataset = TUDataset(root='/tmp/ENZYMES', name='ENZYMES')     # 会下载，不过很快就下载完了
print("数据集的大小(有多少张图)：", len(dataset))
print("图的类别数：", dataset.num_classes)
print("图中结点的特征数：", dataset.num_node_features)

print("第i张图：", dataset[2])
print("图为有向图否：", dataset[2].is_undirected())

输出

数据集的大小(有多少张图)： 600
图的类别数： 6
图中结点的特征数： 3
第i张图： Data(edge_index=[2, 92], x=[25, 3], y=[1])
图为有向图否： True

3.1.2Cora

node-level 数据集载入demo–Cora，依据科学论文之间相互引用关系而构建的Graph数据集，一共包括2708篇论文，共7类：Genetic_Algorithms，Neural_Networks，Probabilistic_Methods，Reinforcement_Learning，Rule_Learning，Theory

# node_level demo

from torch_geometric.datasets import Planetoid

dataset2 = Planetoid(root='/tmp/Cora', name='Cora')   # 自动下载稍微有慢
# 直接上数据仓库中下载数据后放入/tmp/Cora/raw 文件夹着中
# cp ~/Downloads/planetoid-master/data/*cora* ./raw
# 处理完后会多一个processed 文件夹

print("数据集的大小(有多少张图)：", len(dataset2))
print("图的类别数：", dataset2.num_classes)
print("图中结点的特征数：", dataset2.num_node_features)

print("第i张图：", dataset2[0])
print("图为有向图否：", dataset2[0].is_undirected())

print("训练结点数：", dataset2[0].train_mask.sum().item())
print("测试结点数：", dataset2[0].test_mask.sum().item())
print("验证结点数：", dataset2[0].val_mask.sum().item())

输出

数据集的大小(有多少张图)： 1
图的类别数： 7
图中结点的特征数： 1433
第i张图： Data(edge_index=[2, 10556], test_mask=[2708], train_mask=[2708], val_mask=[2708], x=[2708, 1433], y=[2708])
图为有向图否： True
训练结点数： 140
测试结点数： 1000
验证结点数： 500

3.2 PyG自定义数据集

3.2.1Data构建简单的图结构

利用torch_geometric.data.Data()建模下图：四个结点$v_0,v_1,v_2,v_3$，每个结点带有特征向量$[2,1],[5,6],[3,7],[12,0]$，并且每个结点的目标值/目标类别分别为:$0,1,01$

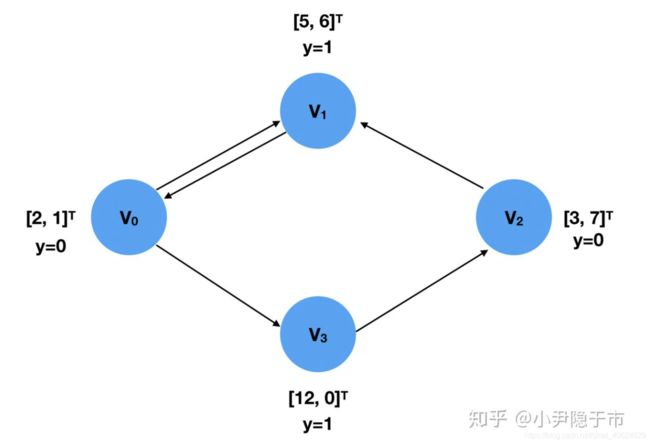
Data()的参数属性：

Data(x=None, edge_index=None, edge_attr=None, y=None, pos=None, normal=None, face=None, **kwargs)
# 参数
# x (Tensor, optional) – 结点的特征矩阵：[num_nodes, num_node_features]. (default: None)
# edge_index (LongTensor, optional) – 结点的连接关系，以COO格式存储 [2, num_edges]. 第一维度为源结点，第二维为目标结点，边可无序存储,可用于计算邻接矩阵。无向图会有2*num_nodes条边。
# y (Tensor, optional) – 图或者结点的目标向量，可以为任意的尺寸. (default: None)
# edge_attr (Tensor, optional) – 边的特征矩阵 [num_edges, num_edge_features]. (default: None)
# pos (Tensor, optional) – Node position matrix with shape [num_nodes, num_dimensions]. (default: None)
# normal (Tensor, optional) – Normal vector matrix with shape [num_nodes, num_dimensions]. (default: None)
# face (LongTensor, optional) – Face adjacency matrix with shape [3, num_faces]. (default: None)

建模代码demo:

import torch
from torch_geometric.data import Data
x = torch.tensor([[2, 1], [5, 6], [3, 7], [12, 0]], dtype=torch.float)     # 每个结点的特征向量
y = torch.tensor([0, 1, 0, 1], dtype=torch.float)  # 结点的目标值
edge_index = torch.tensor([[0, 1, 2, 0, 3], [1, 0, 1, 3, 2]], dtype=torch.long)
data = Data(x=x, y=y, edge_index=edge_index)
print(data)

输出：

Data(edge_index=[2, 5], x=[4, 2], y=[4])
# 方括号中为各个矩阵的尺寸，其中包括5条边，4个维度为2的特征向量，和4个标亮目标值。

3.2.2 Dataset

Dataset，适用于较大的数据集

torch_geometric.data.Dataset

3.2.3 InMemoryDataset

InMemoryDataset，适用于RAM的数据

torch_geometric.data.InMemoryDataset # 继承自torch_geometric.data.Dataset

目前关注的还不是创建自己的数据集合，回头再来

PyTorch geometric官方文档，安装啦，简单使用啦：https://pytorch-geometric.readthedocs.io/en/latest/notes/introduction.html
使用参考博文1–图神经网络库PyTorch geometric（PYG）零基础上手教程：https://zhuanlan.zhihu.com/p/91229616
使用参考博文2–图神经网络之神器——PyTorch Geometric 上手 & 实战：https://zhuanlan.zhihu.com/p/94491664