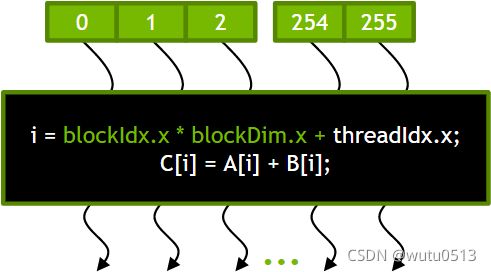
并行计算程序设计(CUDA C)

课程介绍

课程介绍和概述

课程目标

1. 学习如何编写异构并行计算系统并实现
   • 高性能和能效
   • 功能性和可维护性
   • 跨下一代的可扩展性
   • 跨供应商设备的可移植性
2. 技术
   • 并行编程 API、工具和技术
   • 并行算法的原理和模式
   • 处理器架构特性和约束

异构并行计算简介

目标

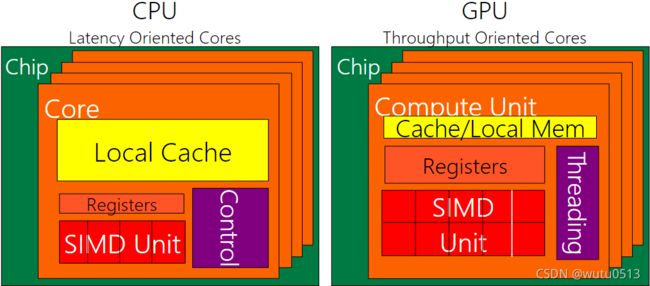
• 了解延迟设备（CPU 内核）和吞吐量设备（GPU 内核）之间的主要区别
• 了解为什么成功的应用程序越来越多地使用这两种类型的设备

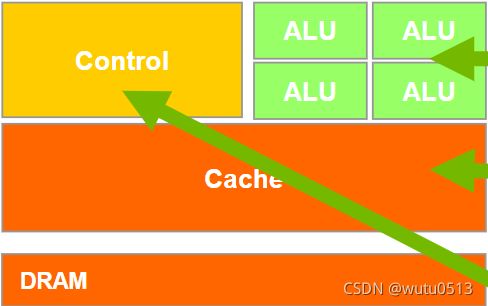
CPU：面向延迟的设计

• 强大的 ALU – 减少操作延迟
• 大缓存 – 将长延迟内存访问转换为短延迟缓存访问
• 复杂的控制
  • 分支预测以减少分支延迟
  • 数据转发以减少数据延迟

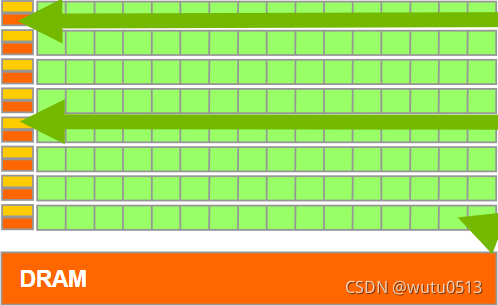
GPU：面向吞吐量的设计

• 小缓存 – 提高内存吞吐量

• 简单控制

  • 无分支预测
  • 无数据转发

• 节能 ALU – 许多、长延迟但大量流水线以实现高吞吐量

• 需要大量线程来容忍延迟

  • 线程逻辑
  • 线程状态

CPU 和 GPU 的设计非常不同

好的应用同时使用GPU和CPU

• 对于顺序代码，CPU 可以比 GPU 快 10 倍以上
• 对于并行代码，GPU 可以比 CPU 快 10 倍以上

异构并行计算中的可移植性和可扩展性

目标

理解并行编程中可扩展性和可移植性的重要性和本质

可扩展性

• 相同的应用程序在新一代内核上可以高效运行

• 相同的应用程序在更多相同的内核上可以高效运行

可移植性

• 同一个应用程序在不同类型的内核上可以高效运行
• 相同的应用程序在具有不同组织和接口的系统上可以高效运行

CUDA C介绍

CUDA C vs. Thrust vs. CUDA Libraries

加速应用程序的方法

1. Libraries — 易于使用 最高性能
2. Compiler Directives — 易于使用的便携式代码
3. Programming Languages — 最高性能 最高灵活性

Libraries

• Ease of use ：使用库可以实现 GPU 加速，而无需深入了解 GPU 编程
• “Drop-in” ：许多 GPU 加速库遵循标准 API，从而以最少的代码更改实现加速
• 质量：库提供了在广泛的应用程序中遇到的功能的高质量实现

Vector Addition in Thrust

thrust::device_vector deviceInput1(inputLength);
thrust::device_vector deviceInput2(inputLength);
thrust::device_vector deviceOutput(inputLength);

thrust::copy(hostInput1, hostInput1 + inputLength, deviceInput1.begin());
thrust::copy(hostInput2, hostInput2 + inputLength, deviceInput2.begin());

thrust::transform(deviceInput1.begin(), deviceInput1.end(), deviceInput2.begin(), deviceOutput.begin(), thrust::plus());

Compiler Directives

• Ease of use：编译器负责并行管理和数据移动的细节
• Portable(便携式的)：代码是通用的，不特定于任何类型的硬件，可以部署成多种语言
• Uncertain：代码性能可能因编译器版本而异

OpenACC

• Compiler directives for C, C++, and FORTRAN

#pragma acc parallel loop 
copyin(input1[0:inputLength],input2[0:inputLength]),  
copyout(output[0:inputLength])
for(i = 0; i < inputLength; ++i) {
	output[i] = input1[i] + input2[i];
}

Programming Languages

• Performance：程序员可以最好地控制并行性和数据移动
• Flexible：计算不需要适合一组有限的库模式或指令类型
• Verbose(冗长的)：程序员往往需要表达更多的细节

内存分配和数据移动 API 函数

目标

学习CUDA主机代码中的基本API函数

• 设备内存分配
• 主机设备数据传输

数据并行 - 向量加法示例

vector A A[0] A[1] A[2] … A[N-1]

​ + + + +

vector B B[0] B[1] B[2] … B[N-1]

​ = = = =

vector C C[0] C[1] C[2] … C[N-1]

向量加法 – 传统 C 代码

// Compute vector sum C = A + B
void vecAdd(float *h_A, float *h_B, float *h_C, int n)
{
	int i;
	for (i = 0; i<n; i++) 
        h_C[i] = h_A[i] + h_B[i];
}

int main()
{
	// Memory allocation for h_A, h_B, and h_C
	// I/O to read h_A and h_B, N elements
	...
	vecAdd(h_A, h_B, h_C, N);
}

异构计算 vecAdd CUDA Host Code

#include 
void vecAdd(float *h_A, float *h_B, float *h_C, int n)
{
	int size = n* sizeof(float); 
    float *d_A, *d_B, *d_C;
    // Part 1
    // Allocate device memory for A, B, and C
    // copy A and B to device memory 
    
    // Part 2
    // Kernel launch code – the device performs the actual vector addition
    
    // Part 3
    // copy C from the device memory
    // Free device vectors
}

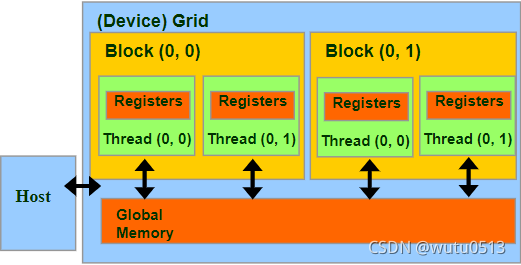
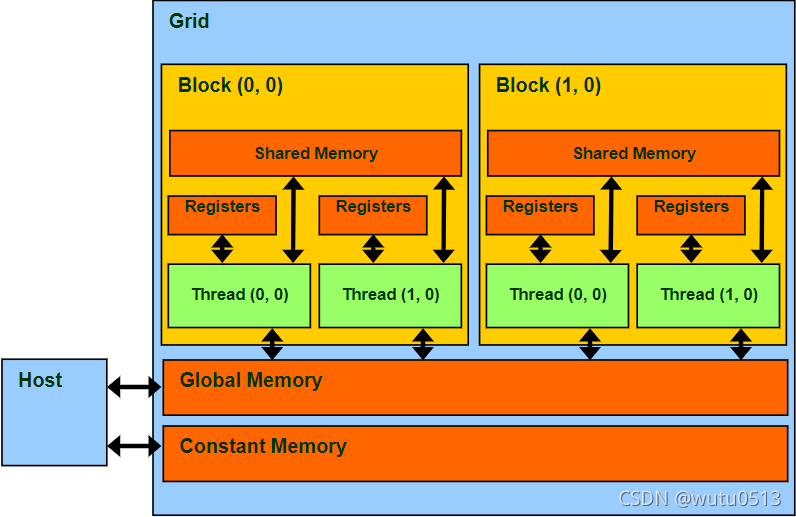
CUDA内存部分概述

设备代码可以：

• R/W 每个线程寄存器
• R/W 全共享全局内存

主机代码可以

• 向/从每个网格全局内存传输数据

CUDA 设备内存管理 API 函数

• cudaMalloc() ：在设备全局内存中分配一个对象
  • 参数1：指向已分配对象的指针的地址
  • 参数2：已分配对象的大小（以字节为单位）
• cudaFree()：从设备全局内存中释放对象
  • 参数：指向释放对象的指针
• cudaMemcpy()：内存数据传输
  • 参数1：指向目的地的指针
  • 参数2：指向源的指针
  • 参数3：复制的字节数
  • 参数4：转移类型/方向

Vector Addition Host Code

void vecAdd(float *h_A, float *h_B, float *h_C, int n)
{
    int size = n * sizeof(float); float *d_A, *d_B, *d_C;
    cudaMalloc((void **) &d_A, size);    
    cudaMemcpy(d_A, h_A, size, cudaMemcpyHostToDevice);
    cudaMalloc((void **) &d_B, size);
    cudaMemcpy(d_B, h_B, size, cudaMemcpyHostToDevice);
    cudaMalloc((void **) &d_C, size);
    
    // Kernel invocation code – to be shown later
    
    cudaMemcpy(h_C, d_C, size, cudaMemcpyDeviceToHost);
    cudaFree(d_A); cudaFree(d_B); cudaFree (d_C);
}

In Practice, Check for API Errors in Host Code

cudaError_t err = cudaMalloc((void **) &d_A, size);
if (err != cudaSuccess)  {
	printf(“%s in %s at line %d\n”, cudaGetErrorString(err), __FILE__, __LINE__);
	exit(EXIT_FAILURE);
}

线程和内核函数

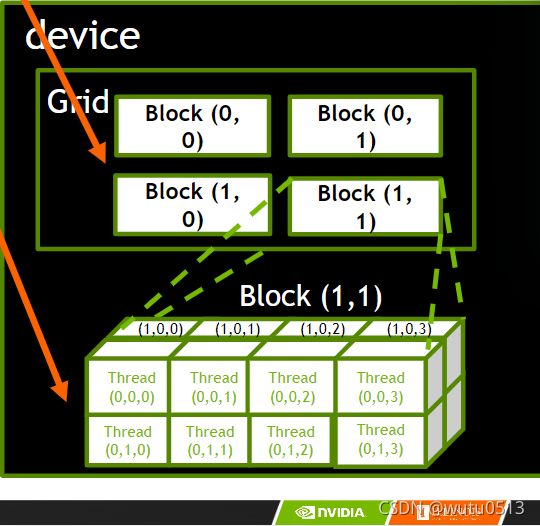
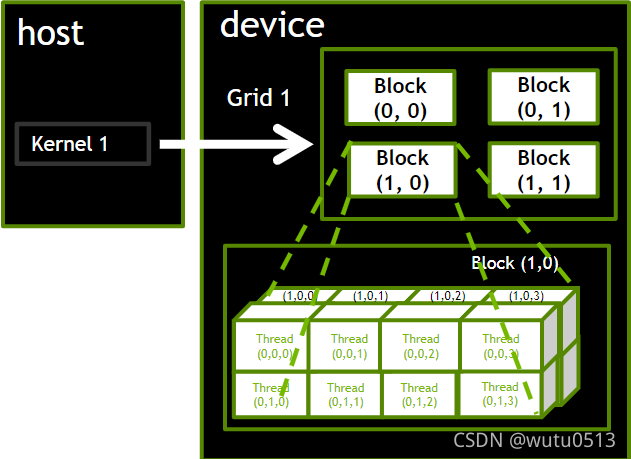
并行线程数组

• CUDA 内核由线程网格（数组）执行
  • 网格中的所有线程运行相同的内核代码(Single Program Multiple Data)
  • 每个线程都有用于计算内存地址和做出控制决策的索引

Thread Blocks(线程块)：可扩展的合作

• 将线程数组分成多个块
  • 块内的线程通过共享内存、原子操作和屏障同步进行协作
  • 不同块中的线程不交互

blockIdx 和 threadIdx

• 每个线程使用索引来决定要处理的数据
  • blockIdx: 1D, 2D, or 3D (CUDA 4.0)
  • threadIdx: 1D, 2D, or 3D

CUDA 工具包简介

略 哈哈哈

CUDA 并行模型

基于内核的 SPMD 并行编程

示例：向量加法内核

Device Code

// Compute vector sum C = A + B
// Each thread performs one pair-wise addition

__global__
void vecAddKernel(float* A, float* B, float* C, int n)
{
	int i = threadIdx.x + blockDim.x * blockIdx.x;
	if(i < n) 
		C[i] = A[i] + B[i];
}

Host Code

void vecAdd(float* h_A, float* h_B, float* h_C, int n)
{
	// d_A, d_B, d_C allocations and copies omitted 
	// Run ceil(n/256.0) blocks of 256 threads each
	vecAddKernel<<>>(d_A, d_B, d_C, n);
}

更多关于内核启动（Host Code）

void vecAdd(float* h_A, float* h_B, float* h_C, int n)
{
	dim3 DimGrid((n - 1)/256 + 1, 1, 1);
	dim3 DimBlock(256, 1, 1);
	vecAddKernel<<>>(d_A, d_B, d_C, n);
}

更多关于 CUDA 函数声明

	执行于	从哪调用
_device_	device	device
_global_	device	host
_host_	host	host

注：__global__函数必须返回 void

多维内核配置

目标

了解多维网格

• 多维块和线程索引
• 将块/线程索引映射到数据索引

一个多维网格示例

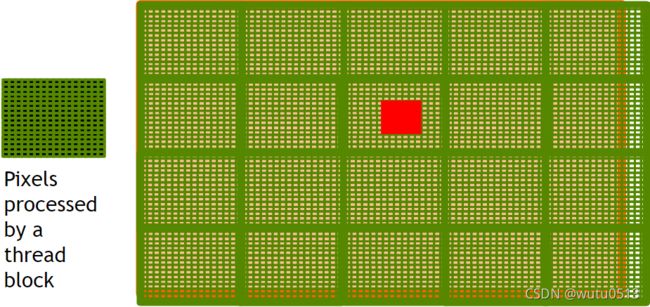
使用2D grid 处理图片

PictureKernel的源代码

将每个像素值缩放 2.0

__global__ void PictureKernel(float* d_Pin, float* d_Pout, int height, int width)
{
    // Calculate the row # of the d_Pin and d_Pout element
    int Row = blockIdx.y*blockDim.y + threadIdx.y;
    
    // Calculate the column # of the d_Pin and d_Pout element
    int Col = blockIdx.x*blockDim.x + threadIdx.x;
    
    // each thread computes one element of d_Pout if in range
    if ((Row < height) && (Col < width)) {
    	d_Pout[Row*width+Col] = 2.0*d_Pin[Row*width+Col];
    }
}

用于启动 PictureKernel 的Host Code

// assume that the picture is m × n, 
// m pixels in y dimension and n pixels in x dimension
// input d_Pin has been allocated on and copied to device
// output d_Pout has been allocated on device
...
dim3 DimGrid((n-1)/16 + 1, (m-1)/16 + 1, 1);
dim3 DimBlock(16, 16, 1);
PictureKernel<<>>(d_Pin, d_Pout, m, n);
...

彩色到灰度图像处理示例

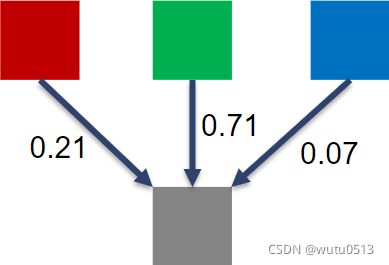
RGB 到灰度转换

颜色计算公式

RGB 到灰度转换代码

#define CHANNELS 3 // we have 3 channels corresponding to RGB
// The input image is encoded as unsigned characters [0, 255]

__global__ void colorConvert(unsigned char * grayImage,
unsigned char * rgbImage,int width, int height) {
	int x = threadIdx.x + blockIdx.x * blockDim.x;
	int y = threadIdx.y + blockIdx.y * blockDim.y;

	if (x < width && y < height) {
		// get 1D coordinate for the grayscale image
		int grayOffset = y*width + x;
		// one can think of the RGB image having
        // CHANNEL times columns than the gray scale image
        int rgbOffset = grayOffset*CHANNELS;
        unsigned char r =  rgbImage[rgbOffset ]; // red value for pixel
        unsigned char g = rgbImage[rgbOffset + 2]; // green value for pixel
        unsigned char b = rgbImage[rgbOffset + 3]; // blue value for pixel
        // perform the rescaling and store it
        // We multiply by floating point constants
        grayImage[grayOffset] = 0.21f*r + 0.71f*g + 0.07f*b;
	}
}

图像模糊示例

模糊框

__global__
void blurKernel(unsigned char * in, unsigned char * out, int w, int h) {
    int Col  = blockIdx.x * blockDim.x + threadIdx.x;
    int Row  = blockIdx.y * blockDim.y + threadIdx.y;

    if (Col < w && Row < h) {
		int pixVal = 0;
        int pixels = 0;
        
		// Get the average of the surrounding 2xBLUR_SIZE x 2xBLUR_SIZE box
        for(int blurRow = -BLUR_SIZE; blurRow < BLUR_SIZE+1; ++blurRow) {
			for(int blurCol = -BLUR_SIZE; blurCol < BLUR_SIZE+1; ++blurCol) {
                int curRow = Row + blurRow;
                int curCol = Col + blurCol;
                // Verify we have a valid image pixel
                if(curRow > -1 && curRow < h && curCol > -1 && curCol < w) {
                	pixVal += in[curRow * w + curCol];
                	pixels++; // Keep track of number of pixels in the accumulated total
                }
			}
		}
        
		// Write our new pixel value out
		out[Row * w + Col] = (unsigned char)(pixVal / pixels);
	}
}

线程调度

目标

了解 CUDA 内核如何利用硬件执行资源

• 将线程块分配给执行资源
• 执行资源的容量限制
• 零开销线程调度

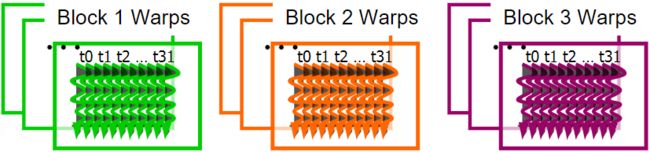
warp 示例

如果将 3 个块分配给一个 SM，每个块有 256 个线程，那么一个 SM 中有多少个 Warp？

• 每个 Block 分为 256/32 = 8 Warps
• 有 8 * 3 = 24 Warps

线程调度（续）

SM 实现零开销 warp 调度

• 下一条指令的操作数可供消费的 Warp 有资格执行
• 基于优先调度策略选择符合条件的 Warp 执行
• 一个 warp 中的所有线程在被选中时执行相同的指令

注意事项

对于使用多个块的矩阵乘法，我应该为 Fermi 使用 8X8、16X16 还是 32X32 块？

• 对于 8X8，我们每个块有 64 个线程。由于每个 SM 最多可以占用 1536 个线程，这相当于 24 个块。但是，每个 SM 最多只能占用 8 个 Blocks，每个 SM 只能有 512 个线程！
• 对于 16X16，我们每个块有 256 个线程。由于每个 SM 最多可以占用 1536 个线程，因此它最多可以占用 6 个块并实现满容量，除非其他资源考虑无效。
• 对于 32X32，我们每个块有 1024 个线程。Fermi 的 SM 中只能容纳一个块。仅使用 SM 线程容量的 2/3。

内存和数据局部性

CUDA Memories

目标

学习在并行程序中有效地使用 CUDA 内存类型

• 内存访问效率的重要性
• 寄存器、共享内存、全局内存
• 范围和生命周期

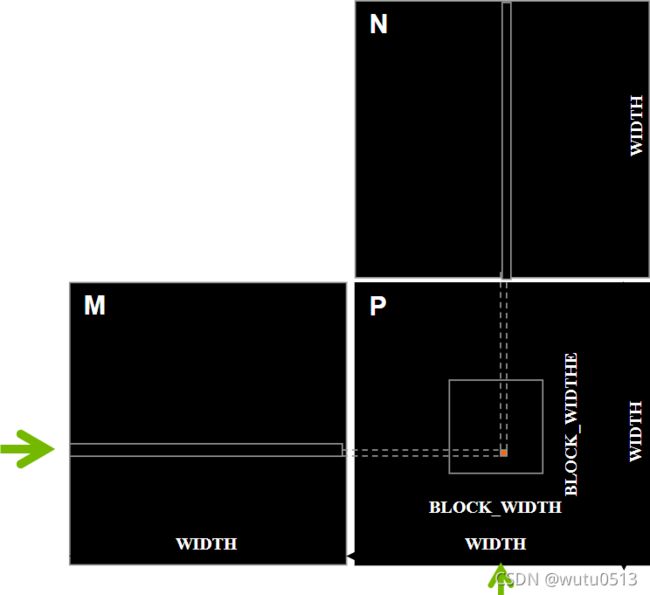
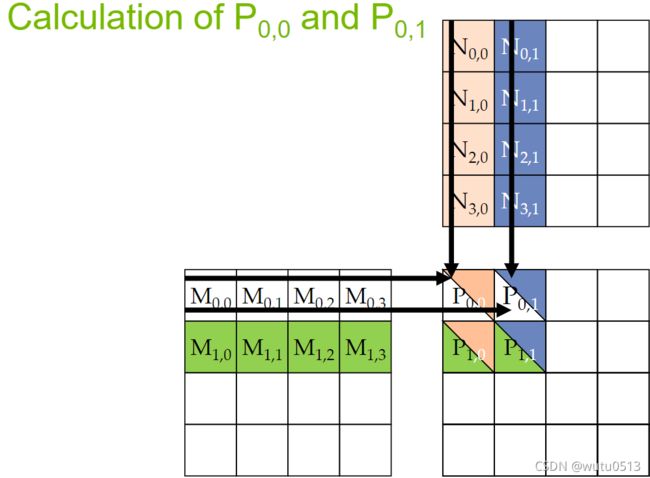
矩阵乘法

一个基本的矩阵乘法

__global__ void MatrixMulKernel(float* M, float* N, float* P, int Width) {
    // Calculate the row index of the P element and M
    int Row = blockIdx.y*blockDim.y+threadIdx.y;
    // Calculate the column index of P and N
    int Col = blockIdx.x*blockDim.x+threadIdx.x;
    if ((Row < Width) && (Col < Width)) {
    	float Pvalue = 0;
    	// each thread computes one element of the block sub-matrix
		for (int k = 0; k < Width; ++k) {
			Pvalue += M[Row*Width+k]*N[k*Width+Col];
		}
		P[Row*Width+Col] = Pvalue;
	}
}

对线程进行分析：

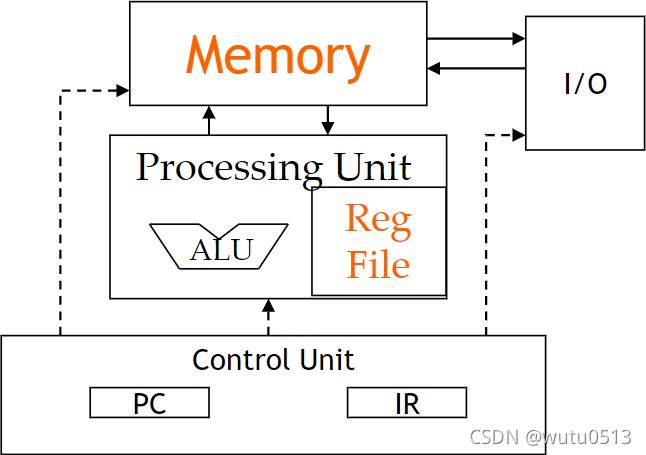
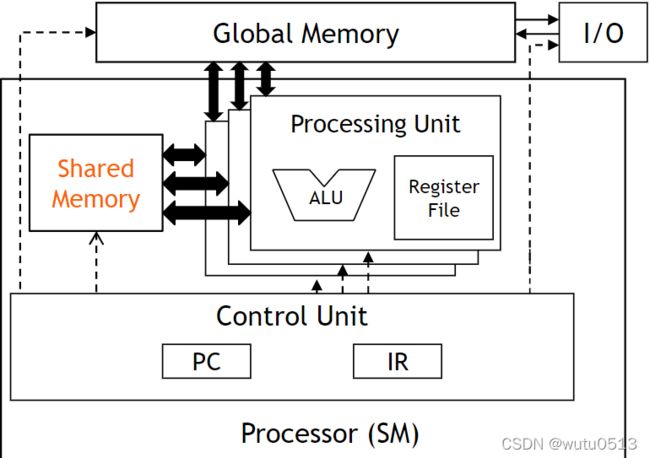
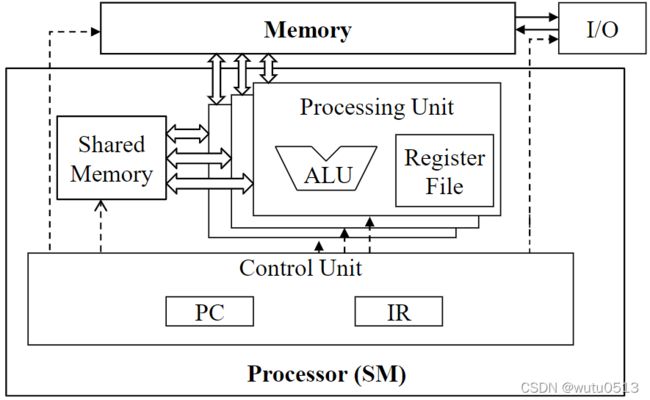
冯诺依曼模型中的存储器和寄存器

CUDA 内存的程序员视图

声明 CUDA 变量

变量声明	Memory	Scope	Lifetime
int LocalVar;	register	thread	thread
_device_ _shared_ int SharedVar;	shared	block	block
_device_ int GlobalVar;	global	grid	application
_device_ _constant_ int ConstantVar;	constant	grid	application

注：__device__ 在与 _shared_ 或 _constant_ 一起使用时是可选的

CUDA 中的共享内存

一种特殊类型的内存，其内容在内核源代码中明确定义和使用

• 每个 SM 中的一个
• 以比全局内存高得多的速度（在延迟和吞吐量方面）访问
• 访问和共享范围—线程块
• 生命周期—线程块，对应线程结束执行后内容会消失
• 通过内存加载/存储指令访问
• 计算机体系结构中的一种暂存内存形式

CUDA 内存的硬件视图

Tiled 并行算法

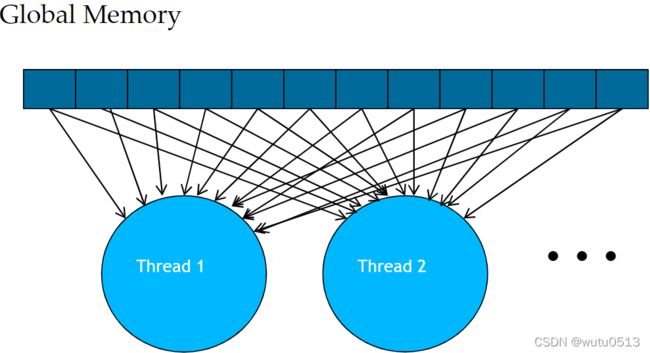
基本矩阵乘法内核的全局内存访问模式

Tiling/Blocking

将全局内存内容划分为tiles
将线程的计算集中在每个时间点的一个或少量tiles上

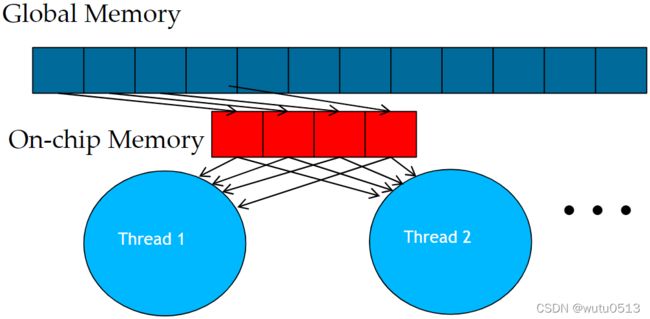
Tiling的基本概念

在拥堵的交通系统中，显着减少车辆可以大大改善所有车辆看到的延迟

• 拼车

拼车需要同步

好：当人们有相似的时间表时

不好：当人们的日程安排非常不同时

在Tiling中

Tiling技术概要

• 识别由多个线程访问的全局内存内容块
• 将块从全局内存加载到片上内存
• 使用屏障同步来确保所有线程都准备好开始阶段
• 让多个线程访问它们的数据来自片上存储器
• 使用屏障同步来确保所有线程都完成了当前阶段
• 移动到下一个 tile

Tiled矩阵乘法

目标

理解矩阵乘法的tiled并行算法的设计

• 加载tile
• 分阶段执行
• 屏障同步

屏障同步

• 同步块中的所有线程

  • __syncthreads()

• 同一块中的所有线程必须到达__syncthreads() 才能继续前进

• 最适合用于协调分阶段执行tiled 算法

  • 确保平铺的所有元素在阶段开始时加载
  • 确保在阶段结束时消耗图块的所有元素

Tiled矩阵乘法核心

目标

学习编写Tiled矩阵乘法内核

• 加载和使用切片进行矩阵乘法
• 屏障同步，共享内存
• 资源注意事项
• 为简单起见，假设 Width 是tile大小的倍数

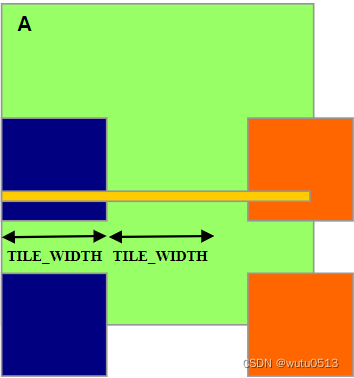
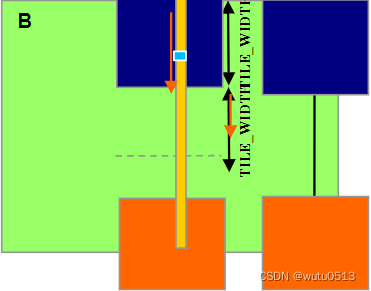
加载

​ Loading Input Tile 0 of M (Phase 0) Loading Input Tile 0 of N (Phase 0)

​ Loading Input Tile 1 of M (Phase 1) Loading Input Tile 1 of N (Phase 1)

M 和 N 是动态分配的 - 使用一维索引

M[Row][p*TILE_WIDTH+tx]
—> M[Row*Width + p*TILE_WIDTH + tx]

N[p*TILE_WIDTH+ty][Col]
—> N[(p*TILE_WIDTH+ty)*Width + Col]

Tiled矩阵乘法核心

__global__ void MatrixMulKernel(float* M, float* N, float* P, Int Width){
	__shared__ float ds_M[TILE_WIDTH][TILE_WIDTH];
	__shared__ float ds_N[TILE_WIDTH][TILE_WIDTH];

    int bx = blockIdx.x;
    int by = blockIdx.y;
	int tx = threadIdx.x; 
    int ty = threadIdx.y;
 
    int Row = by * blockDim.y + ty;
	int Col = bx * blockDim.x + tx;
	float Pvalue = 0;

    // Loop over the M and N tiles required to compute the P element
	for (int p = 0; p < n/TILE_WIDTH; ++p) {
		// Collaborative loading of M and N tiles into shared memory
        ds_M[ty][tx] = M[Row*Width + p*TILE_WIDTH + tx];
        ds_N[ty][tx] = N[(t*TILE_WIDTH+ty)*Width + Col];
        __syncthreads();//等待块中其他线程同步

        for (int i = 0; i < TILE_WIDTH; ++i){
            Pvalue += ds_M[ty][i] * ds_N[i][tx];
        }
		__synchthreads();//等待其他线程计算完，因为Pvalue要用到下一个块的计算
	}
	P[Row*Width+Col] = Pvalue;
}

Tile（线程块）大小注意事项

• 每个线程块应该有多个线程

  • TILE_WIDTH 是16的给出 16*16 = 256 个线程
  • TILE_WIDTH 是32的给出 32*32 = 1024 个线程

• 对于 16，在每个阶段，每个块从全局内存执行 2256 = 512 次浮点加载，用于 256 * (216) = 8,192 次 mul/add 操作。（每个内存加载 16 次浮点运算）

• 对于 32，在每个阶段，每个块从全局内存执行 21024 = 2048 次浮点加载，执行 1024 * (232) = 65,536 次 mul/add 操作。 (每个内存加载32次浮点运算)

共享内存和线程

• 对于具有 16KB 共享内存的 SM

  • 共享内存大小取决于实现！
  • 对于 TILE_WIDTH = 16，每个线程块使用 2*256*4B = 2KB 的共享内存
  • 下一个 TILE_WIDTH 32 将导致每个线程块使用 2*32*32*4 Byte= 8K Byte 共享内存，从而允许 2 个线程块同时处于活动状态

• 每个 __syncthread() 可以减少一个块的活动线程数

  • 更多的线程块可能是有利的

在Tiled算法中处理任意矩阵大小

处理任意大小的矩阵

• 到目前为止，我们介绍的 tiled 矩阵乘法内核只能处理维度（宽度）是平铺宽度（TILE_WIDTH）倍数的方阵。
• 然而，实际应用程序需要处理任意大小的矩阵。
• 可以将行和列填充（添加元素）为切片大小的倍数，但会产生大量的空间和数据传输时间开销。

一个“简单”的解决方案

• 当一个线程要加载任何输入元素时，测试它是否在有效的索引范围内
  • 如果有效，继续加载
  • 否则，不加载，只写一个 0
• 基本原理：0 值将确保乘加步骤不会影响输出元素的最终值
• 加载输入元素的测试条件与计算输出 P 元素的测试不同
  • 不计算有效 P 元素的线程仍然可以参与加载输入 tile 元素

输入 M tile 的边界条件

• 每个线程加载
  • M[Row][p*TILE_WIDTH+tx]
  • M[Row*Width + p*TILE_WIDTH+tx]
• 需要测试
  • (Row < Width) && (p*TILE_WIDTH+tx < Width)
  • 如果为真，则加载 M 元素
  • 否则，加载 0

输入 N tile 的边界条件

• 每个线程加载
  • N[p*TILE_WIDTH+ty][Col]
  • N[(p*TILE_WIDTH+ty)*Width+ Col]
• 需要测试
  • (p*TILE_WIDTH+ty < Width) && (Col< Width)
  • 如果为真，则加载 N 元素
  • 否则，加载 0

__global__ void MatrixMul_sm(int* p_A, int* p_B, int* p_C, int A_row, int A_col, int B_col) {
	__shared__ double sharedM[TILE_SIZE][TILE_SIZE];
	__shared__ double sharedN[TILE_SIZE][TILE_SIZE];

	int bx = blockIdx.x;
	int by = blockIdx.y;
	int tx = threadIdx.x;
	int ty = threadIdx.y;

	int row = by * TILE_SIZE + ty;
	int col = bx * TILE_SIZE + tx;

	int Pvalue = 0;

	for (int i = 0; i < (int)(ceil((double)A_col / TILE_SIZE)); i++) {
		if (i * TILE_SIZE + tx < A_col && row < A_row) {
			sharedM[ty][tx] = p_A[row * A_col + i * TILE_SIZE + tx];
		}else {
			sharedM[ty][tx] = 0;
		}

		if (i * TILE_SIZE + ty < A_col && col < B_col) {
			sharedN[ty][tx] = p_B[(i * TILE_SIZE + ty) * B_col + col];
		}else {
			sharedN[ty][tx] = 0;
		}
        
		__syncthreads();
		for (int j = 0; j < TILE_SIZE; j++) {
			Pvalue += sharedM[ty][j] * sharedN[j][tx];
		}
		__syncthreads();
	}

	if (row < A_row && col < B_col) {
		p_C[row * B_col + col] = Pvalue;
	}
}

简易版

for(int p = 0; p < (Width - 1) / TILE_WIDTH + 1; P++){
    if(Row < Width && p * TILE_WIDTH + tx < Width){
        ds_M[ty][tx] = M[Row*Width + p*TILE_WIDTH + tx];
    }else{
        ds_M[ty][tx] = 0.0;
    }
    
    if(p*TILE_WIDTH + ty < Width && Col < Width){
        ds_N[ty][tx] = N[(p*TILE_WIDTH + ty)*Width + Col];
    }else{
        ds_N[ty][tx] = 0.0;
    }
    __syncthreads();
    
    if(Row < Width && Col < Width){
        for(int i = 0;i < TILE_WIDTH; ++i){
            Pvalue += ds_M[ty][i]*ds_N[i][tx];
        }
    }
    __syncthreads();
}
if(Row < Width && Col < Width){
    P[Row*Width + Col] = Pvalue;
}

一些要点

• 对于每个线程，条件是不同的
  • 加载 M 元素
  • 加载 N 元素
  • 计算和存储输出元素
• 对于大矩阵，控制发散的影响应该很小

处理一般矩形矩阵

• 一般来说，矩阵乘法是根据矩形矩阵定义的
  • j x k M 矩阵乘以 k x l N 矩阵产生 j x l P 矩阵
• 我们已经介绍了方阵乘法，一种特殊情况
• 核函数需要泛化处理一般矩形矩阵
  • Width 参数被三个参数替换：j、k、l
  • 当Width用来指M的高度或P的高度时，替换为j
  • 当Width用来指M的宽度或N的高度时，替换为k
  • 当Width用来指代N的宽度或P的宽度，替换为l

线程执行效率

Warps 和 SIMD 硬件

目标

了解 CUDA 线程如何在 SIMD 硬件上执行

• Warp 分区
• SIMD 硬件
• Control divergence

作为调度单位的Warps

每个块分为 32 线程 Warp

• 一种实现技术，不是 CUDA 编程模型的一部分
• Warps 是 SM 中的调度单元
• warp 中的线程以单指令多数据 (SIMD) 方式执行
• warp 中的线程数在未来几代可能会有所不同

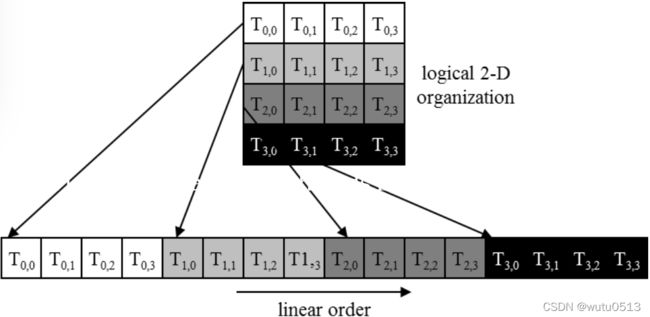
多维线程块中的warps

线程块首先按行主顺序线性化为一维

• 首先是 x 维度，然后是 y 维度，最后是 z 维度

线性化后对块进行分区

• 线性化线程块被分区
  • warp内的线程索引是连续的并且不断增加
  • Warp 0 从线程 0 开始
• 跨设备分区方案一致
  • 因此，您可以在控制流中使用这些知识
  • 但是，warp的确切大小可能会代代相传
• 不要依赖warp内或warp之间的任何排序
  • 如果线程之间存在任何依赖关系，则必须 __syncthreads() 才能获得正确的结果（稍后会详细介绍）。

SM 是 SIMD 处理器

指令获取、解码和控制的控制单元在多个处理单元之间共享

• 控制开销最小化（模块 1）

Warp 中线程间的 SIMD 执行

Warp 中的所有线程必须在任何时间点执行相同的指令

如果所有线程都遵循相同的控制流路径，这将有效地工作

• 所有 if-then-else 语句都做出相同的决定
• 所有循环迭代相同的次数

Control Divergence

当 warp 中的线程通过做出不同的控制决策而采取不同的控制流路径时，就会发生控制发散

• 一些采用 then 路径，另一些采用 if 语句的 else 路径
• 一些线程与其他线程采用不同数量的循环迭代

采取不同路径的线程的执行在当前的 GPU 中被序列化

• 一个 warp 中的线程所采用的控制路径一次遍历一个，直到没有更多的路径。
• 在每个路径的执行过程中，所有采用该路径的线程都将并行执行
• 考虑嵌套控制流语句时，不同路径的数量可能很大

Control Divergence 例子

• 当分支或循环条件是线程索引的函数时，可能会出现分歧
• 具有分歧的内核语句示例：
  • if (threadIdx.x > 2) { }
  • 这为块中的线程创建了两个不同的控制路径
  • 决策粒度 < warp大小；线程 0、1 和 2 遵循与第一个warp中的其余线程不同的路径
• 没有发散的例子：
  • If (blockIdx.x > 2) { }
  • 决策粒度是块大小的倍数；任何给定 warp 中的所有线程都遵循相同的路径

分析 1,000 个元素的向量大小

• 假设块大小为 256 个线程

  • 每个块中有 8 个 warp

• 块 0、1 和 2 中的所有线程都在有效范围内

  • i 的值从 0 到 767（3*256 - 1）
  • 这三个块有24个 warp，没有一个会有控制发散

• Block 3 中的大多数warp不会控制发散

  • warp 0-6中的线程都在有效范围内，因此没有控制发散

• Block 3 中的一个 warp 将具有控制发散

  • i 值为 992-999 的线程都在有效范围内
  • i 值为 1000-1023 的线程将超出有效范围

• 序列化对控制发散的影响会很小

  • 32 个 warp 中有 1 个具有控制发散
  • 对性能的影响可能小于 3%

控制发散的性能影响

目标

学习分析控制发散对性能的影响

• 边界条件检查
• 控制发散依赖于数据

控制发散的性能影响

边界条件检查对于并行代码的完整功能和健壮性至关重要

• 分块矩阵乘法内核有许多边界条件检查
• 令人担忧的是这些检查可能会导致显着的性能下降

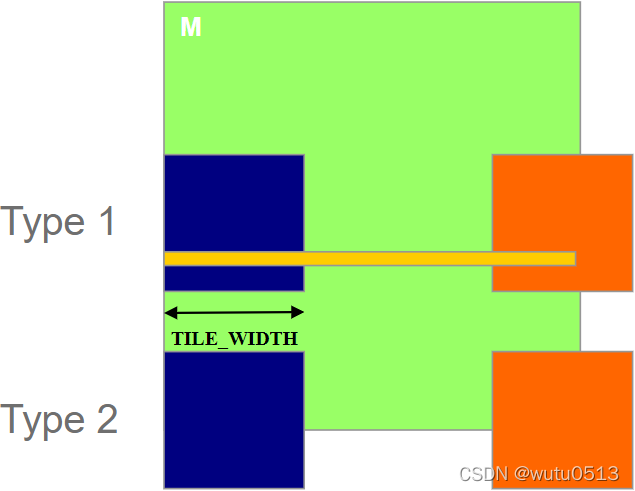
加载M Tiles时的两种方块

• 1 直到最后一个阶段，其tile 都在有效范围内的块。
• 2 tile 部分一直在有效范围之外的块。

控制发散影响分析

• 假设 16x16 tile和线程块
• 每个线程块有 8 个warp (256/32)
• 假设 100x100 的方阵
• 每个线程将经历 7 个阶段（100/16 的上限）
• 有 49 个线程块（每个维度 7 个）

控制加载 M 块的发散度(Type 1)

• 有 42 (6*7) 个 Type 1 blocks，总共 336 (8*42) 个 warp
• 它们都有 7 个阶段，所以有 2352 (336*7) 个 warp 阶段
• warp 只有在最后阶段才有控制发散
• 336 个 warp 阶段有控制发散

控制加载 M 块时的发散（Type 2）

• Type 2：分配加载底部 warp 的7个块，共56（8*7）个warp
• 它们都有 7 个阶段，所以有 392 (56*7) 个warp阶段
• 每个Type 2 块中的前 2 个 warp 将保持在有效范围内，直到最后一个阶段
• 剩余的 6 个 warp 不在有效范围内
• 所以，只有 14 (2*7) 个 warp 阶段有控制发散

注：Type 1 和Type 2见上图

Control Divergence的总体影响

• Type 1 blocks：2352 个warp阶段中的 336 个具有控制发散
• Type 2 blocks：392 个经线阶段中有 14 个具有控制发散
• 性能影响预计小于 12% (350 / 2944 或 (336 + 14)/(2352 + 14))

附加注释

• 加载N个tile时控制发散的影响计算有些不同，留作练习
• 估计的性能影响取决于数据。
  • 对于较大的矩阵，影响将显着较小。
• 一般来说，控制分歧对大型输入数据集的边界条件检查的影响应该是微不足道的。
  • 人们应该毫不犹豫地使用边界检查来确保完整的功能。
• 内核中充满控制流结构的事实并不意味着会出现严重的控制发散
• 我们将在 Parallel Algorithm Patterns 模块中介绍一些自然会导致控制发散（例如并行缩减）的算法模式

内存访问性能

DRAM带宽

目标

了解内存带宽是大规模并行处理器中的一阶性能因素。

• DRAM bursts、存储体和通道
• 所有概念也适用于现代多核处理器

DRAM 核心阵列很慢

从核心阵列中的单元读取是一个非常缓慢的过程

DDR：核心速度 = ½ 接口速度

DDR2/GDDR3：核心速度 = ¼ 接口速度

DDR3/GDDR4：核心速度 = ⅛ 接口速度 - …

未来可能会更糟

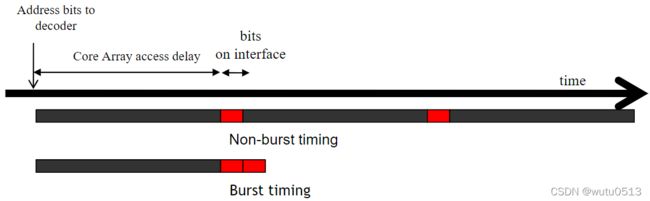
DRAM 突发

对于时钟频率为接口速度 1/N 的 DDR{2,3} SDRAM 内核：

• 从同一行一次性加载（N × 接口宽度）DRAM 位到内部缓冲区，然后以接口速度分 N 步传输

• DDR3/GDDR4：缓冲区宽度 = 8X 接口宽度

DRAM 突发时序示例

现代 DRAM 系统设计为始终以突发模式访问。突发字节被传输到处理器，但当访问不是对连续位置时被丢弃。

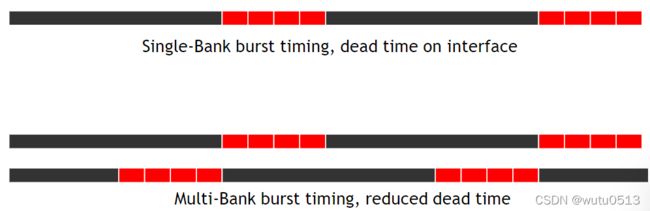
DRAM Bursting with Banking

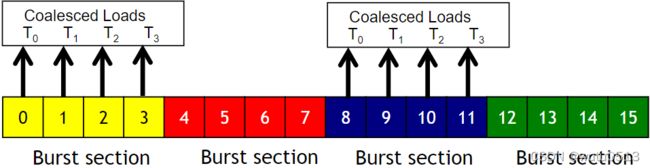
CUDA 中的内存合并

目标

了解内存合并对于有效利用 CUDA 中的内存带宽很重要。

• 它的起源于DRAM burst
• 检查 CUDA 内存访问是否已合并
• 在 CUDA 代码中改进内存合并的技术

DRAM burst – 系统视图

每个地址空间被划分为burst部分

• 每当访问一个位置时，同一部分中的所有其他位置也被传送到处理器

基本示例：16 字节地址空间，4 字节burst部分

• 实际上，我们至少有 4GB 的地址空间，128 字节或更多的burst部分大小

合并内存

当一个warp的所有线程都执行一条加载指令时，如果所有访问的位置都落入同一个突发部分，则只会发出一个DRAM请求，并且访问完全合并。

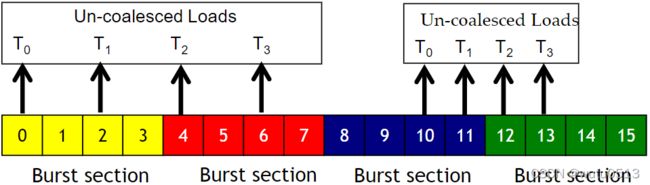
非合并内存访问

当访问的位置跨越突发部分边界时：

• 合并失败
• 发出多个 DRAM 请求
• 访问未完全合并

线程不使用某些访问和传输的字节

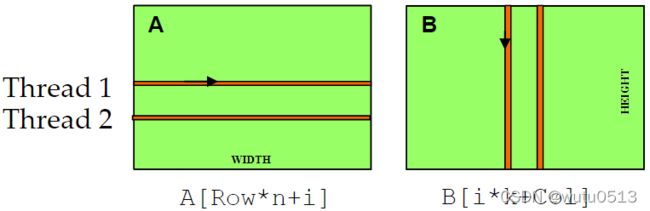
基本矩阵乘法的两种存取模式

i 是内核代码内积循环中的循环计数器，A 是 m × n，B 是 n × k，Col = blockIdx.x*blockDim.x + threadIdx.x
在B矩阵中，是合并内存访问，A矩阵中，不是合并内存访问。

并行计算模式(直方图)

直方图

目标

学习并行直方图计算模式

• 一个重要的、有用的计算
• 就每个线程的输出行为而言，与我们迄今为止所涵盖的所有模式都非常不同
• 理解并行计算中的输出干扰的一个很好的起点

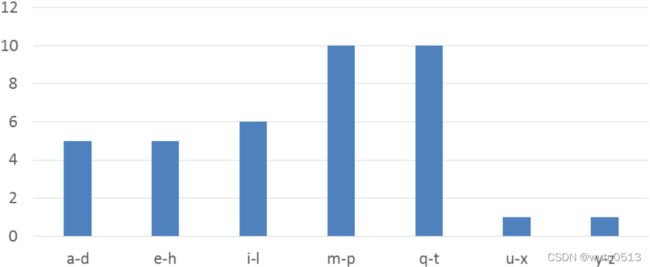
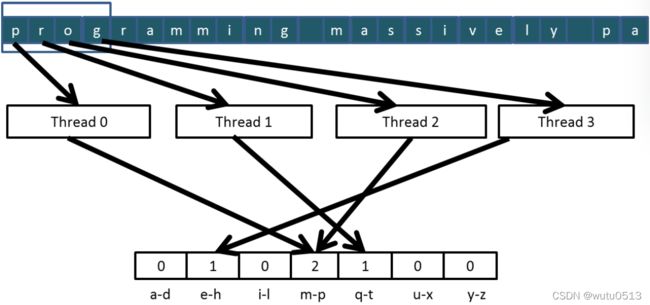
文本直方图示例

• 将 bin 定义为字母表的四个字母部分：a-d、e-h、i-l、m-p、…
• 对于输入字符串中的每个字符，增加相应的 bin 计数器。
• 在短语 “Programming Massively Parallel Processors” 中，输出直方图如下所示：

一种简单的并行直方图算法

• 将输入分成多个部分
• 让每个线程获取输入的一部分
• 每个线程遍历其部分
• 对于每个字母，增加相应的 bin 计数器

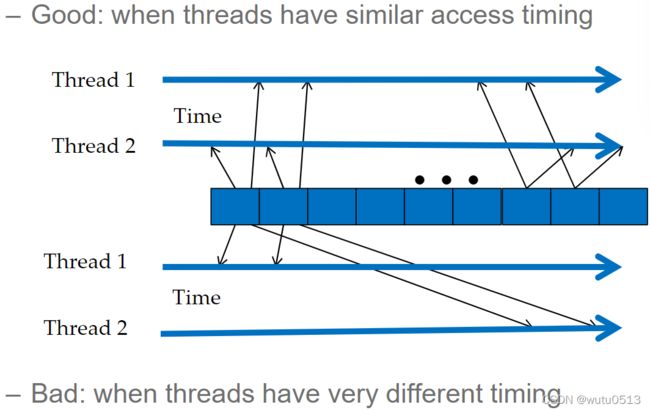
输入分区影响内存访问效率

分段分区导致内存访问效率低下

• 相邻线程不访问相邻内存位置
• 访问未合并
• DRAM 带宽利用率低

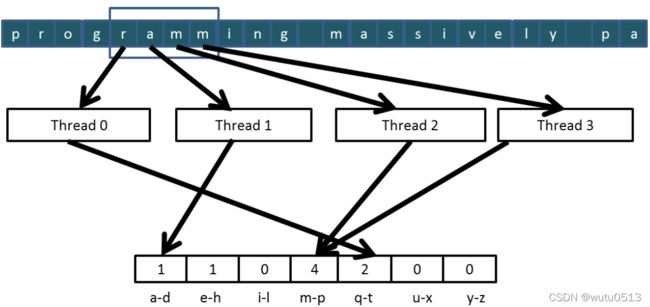
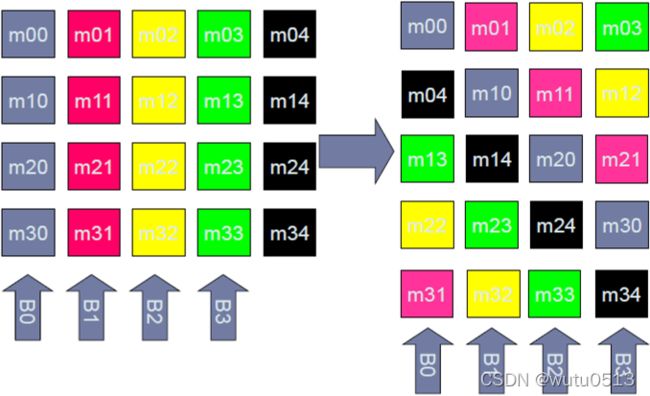
更改为交错分区

• 所有线程处理元素的连续部分
• 他们都移动到下一部分并重复
• 内存访问被合并

交错分区

用于合并和更好的内存访问性能

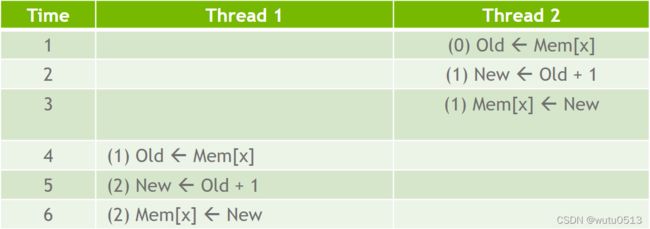
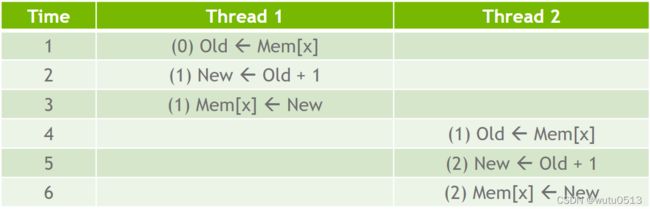
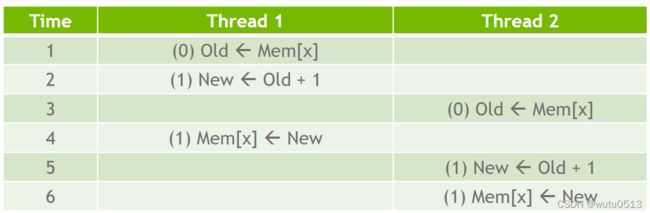
数据竞争简介

目标

理解并行计算中的数据竞争

• 执行读-修改-写操作时可能会发生数据竞争
• 数据竞争可能导致难以重现的错误
• 原子操作旨在消除此类数据竞争

原子操作的目的——确保良好的结果

我们希望的结果：

不希望的结果：

CUDA 中的原子操作

目标

学习在并行程序中使用原子操作

• 原子操作概念
• CUDA 中的原子操作类型
• Intrinsic functions
• 一个基本的直方图内核

原子操作的关键概念

由单个硬件指令对内存位置地址执行的读 - 修改 - 写操作

• 读取旧值，计算新值，并将新值写入该位置

硬件确保在当前原子操作完成之前，没有其他线程可以在同一位置执行另一个读 - 修改 - 写操作

• 尝试在同一位置执行原子操作的任何其他线程通常将被保留在队列中
• 所有线程在同一位置串行执行它们的原子操作

Atomic Add

int atomicAdd(int* address, int val);

从全局或共享内存中的地址指向的位置读取 32 位字 old，计算 (old + val)，并将结果存储回内存中的同一地址。该函数返回 old。

unsigned int atomicAdd(unsigned int* address, unsigned int val);

无符号 32 位整数原子加法。

unsigned long long int atomicAdd(unsigned long long int* address, unsigned long long int val);

无符号 64 位整数原子加法。

float atomicAdd(float* address, float val);

单精度浮点原子加法（能力> 2.0）

一个基本的文本直方图内核

• 内核接收一个指向字节值输入缓冲区的指针
• 每个线程以跨步模式处理输入

__global__ void histo_kernel(unsigned char *buffer, long size, unsigned int *histo) {
	int i = threadIdx.x + blockIdx.x * blockDim.x;
	// stride is total number of threads
	int stride = blockDim.x * gridDim.x;
	// All threads handle blockDim.x * gridDim.x
	// consecutive elements
	while (i < size) {
		atomicAdd(&(histo[buffer[i]]), 1);
		i += stride;
	}
}

• 内核接收一个指向字节值输入缓冲区的指针
• 每个线程以跨步模式处理输入

__global__ void histo_kernel(unsigned char *buffer, long size, unsigned int *histo) {
	int i = threadIdx.x + blockIdx.x * blockDim.x;
	// stride is total number of threads
	int stride = blockDim.x * gridDim.x;
	// All threads handle blockDim.x * gridDim.x
	// consecutive elements
	while (i < size) {
		int alphabet_position = buffer[i] – “a”;
		if (alphabet_position >= 0 && alpha_position < 26) 
			atomicAdd(&(histo[alphabet_position/4]), 1);
		i += stride;
	}
}

原子操作性能

目标

了解原子操作的主要性能考虑

• 原子操作的延迟和吞吐量
• 全局内存上的原子操作
• 共享 L2 缓存上的原子操作
• 共享内存上的原子操作

提高吞吐量的私有化技术

学习通过私有化输出来编写高性能内核

• 私有化作为一种减少延迟、增加吞吐量和减少序列化的技术
• 高性能私有化直方图内核
• 使用共享内存和 L2 缓存原子操作的实际示例

并行计算模式(模板)

卷积

目标

学习卷积，一种重要的方法

• 广泛用于音频、图像和视频处理
• 许多科学和工程应用中使用的模板计算的基础
• 基本的一维和二维卷积核

卷积边界条件

一维：

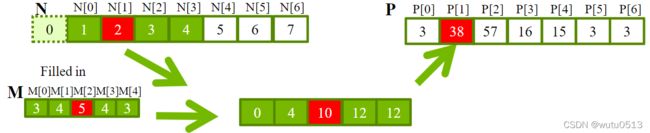
具有边界条件处理的一维卷积核
此内核将有效输入范围之外的所有元素强制为 0

__global__ void convolution_1D_basic_kernel(float *N, float *M, float *P, int Mask_Width, int Width) {
	int i = blockIdx.x*blockDim.x + threadIdx.x;
    
	float Pvalue = 0;
	int N_start_point = i - (Mask_Width/2);
	if (i < Width) {
		for (int j = 0; j < Mask_Width; j++) {
			if (N_start_point + j >= 0 && N_start_point + j < Width) {
				Pvalue += N[N_start_point + j]*M[j];
			}
		}
		P[i] = Pvalue;
    }
}

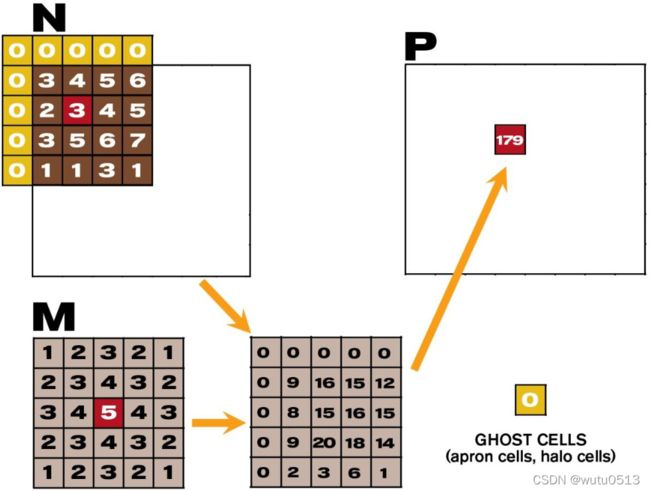
二维:

具有边界条件处理的一维卷积核
此内核将有效输入范围之外的所有元素强制为 0

__global__ void convolution_2D_basic_kernel(unsigned char * in, unsigned char * mask, unsigned char * out, int maskwidth, int w, int h) {
	int Col  = blockIdx.x * blockDim.x + threadIdx.x;
	int Row  = blockIdx.y * blockDim.y + threadIdx.y;
    
	if (Col < w && Row < h) {
		int pixVal = 0;
        
		N_start_col = Col - (maskwidth/2);
		N_start_row = Row - (maskwidth/2);
		// Get the of the surrounding box
		for(int j = 0; j < maskwidth; ++j) {
			for(int k = 0; k < maskwidth; ++k) {
				int curRow = N_Start_row + j;
				int curCol = N_start_col + k;
				// Verify we have a valid image pixel
				if(curRow > -1 && curRow < h && curCol > -1 && curCol < w) {
					pixVal += in[curRow * w + curCol] * mask[j*maskwidth+k];
				}
			}
		}
		// Write our new pixel value out
		out[Row * w + Col] = (unsigned char)(pixVal);
	}
}

Tiled 卷积

目标

了解tiled卷积算法

• tiled算法的一些复杂方面

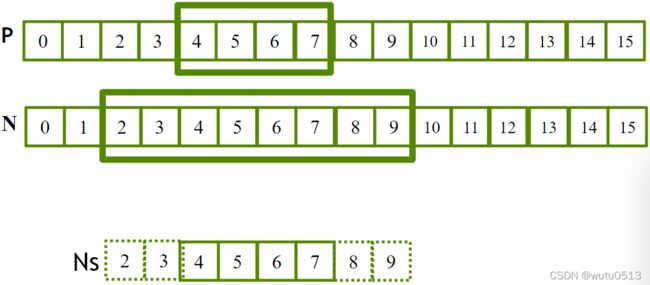
输入数据需求

假设我们想让每个块计算 T 个输出元素

• 需要T + Mask_Width - 1 个输入元素来计算 T 个输出元素
• T + Mask_Width -1 通常不是 T 的倍数，除非 T 值很小
• T 通常明显大于 Mask_Width

两种设计选项

• 设计 1：每个线程块的大小与输出 tile 的大小相匹配
  • 所有线程都参与计算输出元素
  • 一些线程需要将加载跟多输入元素到共享内存中
• 设计 2：每个线程块的大小与输入 tile 的大小相匹配
  • 一些线程不会参与计算输出元素
  • 每个线程将一个输入元素加载到共享内存中

设计 2

float output = 0.0f;
if((index_i >= 0) && (index_i < Width)) {
	Ns[tx] = N[index_i];
} else {
	Ns[tx] = 0.0f;
}

一些线程不参与计算输出

if (threadIdx.x < O_TILE_WIDTH){
    // 只有线程 0 到 O_TILE_WIDTH-1 参与输出的计算。
    
	output = 0.0f;
	for(j = 0; j < Mask_Width; j++) {
		output += M[j] * Ns[j + threadIdx.x];
	}
    // index_o = blockIdx.x*O_TILE_WIDTH + threadIdx.x
	P[index_o] = output;
}

设置块大小

#define O_TILE_WIDTH 1020
#define Mask_Width 5
#define BLOCK_WIDTH (O_TILE_WIDTH + Mask_Width - 1)

dim3 dimBlock(BLOCK_WIDTH, 1, 1);
dim3 dimGrid((Width - 1) / O_TILE_WIDTH + 1, 1, 1)

tile 边界条件

目标

学习写一个二维卷积核

• 二维图像数据类型和 API 函数
• 使用常量缓存
• 2D 中的输入 tile 与输出 tile
• 线程到数据索引映射
• 处理边界条件

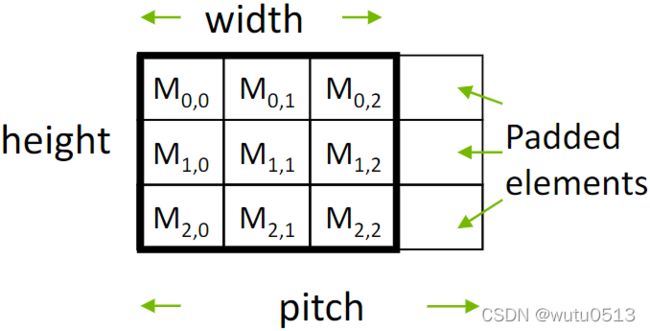
具有自动填充的 2D 图像矩阵

• 有时需要将 2D 矩阵的每一行填充到 DRAM 突发的倍数
  • 所以每一行都从 DRAM 突发边界开始
  • 有效地添加列
  • 这通常由矩阵分配函数自动完成
  • 不同硬件的 Pitch 可能不同
• 示例：将 3X3 矩阵填充到 3X4 矩阵中
  • 高度为 3
  • 宽度为 3
  • 通道为 1（参见 MP 说明）
  • Pitch 为 4
    

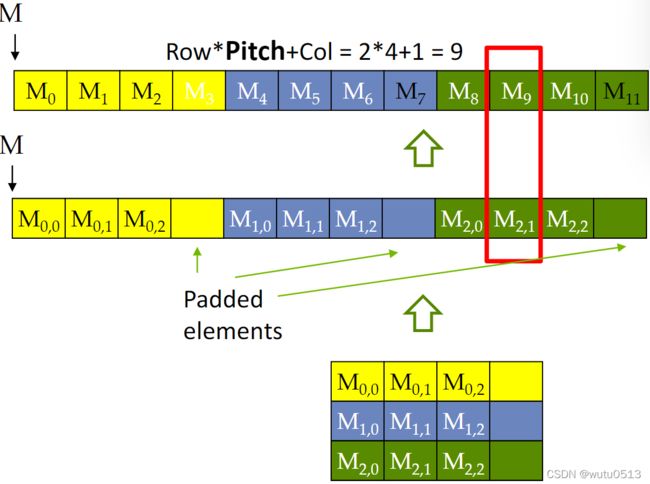
带 Pitch 的行主布局

设置块大小

#define O_TILE_WIDTH 12
#define Mask_Width 5
#define BLOCK_WIDTH (O_TILE_WIDTH + Mask_Width - 1)

dim3 dimBlock(BLOCK_WIDTH, BLOCK_WIDTH, 1);
dim3 dimGrid((Width - 1) / O_TILE_WIDTH + 1, (Height - 1) / O_TILE_WIDTH + 1, 1)

为 Mask 使用常量内存和缓存

• Mask 被所有线程使用，但在卷积核中没有修改
  • 一个 warp 中的所有线程在每个时间点访问相同的位置
• CUDA 设备提供恒定内存，其内容被积极缓存
  • 缓存的值被广播到一个 warp 中的所有线程
  • 有效放大内存带宽，不消耗共享内存
• 对掩码参数使用 const _restrict_ 限定符通知编译器它有资格进行常量缓存，例如：

//部分代码
__global__ void convolution_2D_kernel(float *P, float *N, height, width, channels,     
const float __restrict__ *M) {
    __shared__ float Ns[TILE_SIZE+MAX_MASK_WIDTH-1][TILE_SIZE+MAX_MASK_HEIGHT-1];
    
	int tx = threadIdx.x;
	int ty = threadIdx.y;
	int row_o = blockIdx.y*O_TILE_WIDTH + ty;
	int col_o = blockIdx.x*O_TILE_WIDTH + tx;
    
    int row_i = row_o - 2;
	int col_i = col_o - 2;
    
    if((row_i >= 0) && (row_i < height) && (col_i >= 0)  && (col_i < width)) {
		Ns[ty][tx] = data[row_i * width + col_i];
	} else{
		Ns[ty][tx] = 0.0f;
	}
    
    float output = 0.0f;
	if(ty < O_TILE_WIDTH && tx < O_TILE_WIDTH){
		for(i = 0; i < MASK_WIDTH; i++) {
			for(j = 0; j < MASK_WIDTH; j++) {
				output += M[i][j] * Ns[i+ty][j+tx];
			}
		}
        
        if(row_o < height && col_o < width)
			data[row_o*width + col_o] = output;
    }
}

减少因子：

• 1D: $(O\_TILE\_WIDTH\ast MASK\_WIDTH)/(O\_TILE\_WIDTH+MASK\_WIDTH-1)$
• 2D: $O\_TILE\_WIDT{H}^2\ast MASK\_WIDT{H}^2/(O\_TILE\_WIDTH+MASK\_WIDTH-1{)}^2$

性能调优(存储优化)

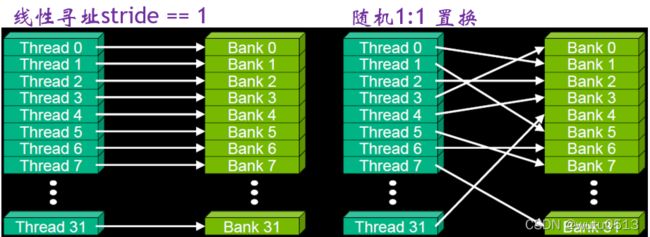
bank conflict

什么是bank conflict

• Bank conflict发生在使用共享内存(Shared Memory)时
• 因为shared mempory是片上的（Cache级别），所以比局部内存（local memory）和全局内存（global memory）快很多。

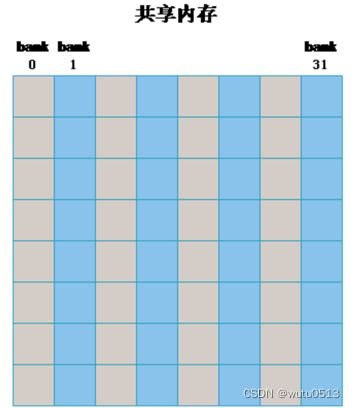
GPU 共享内存中的Bank

如在一个线程块中申请如下的共享内存：_shared_ float sData[32][32];

bank conflict

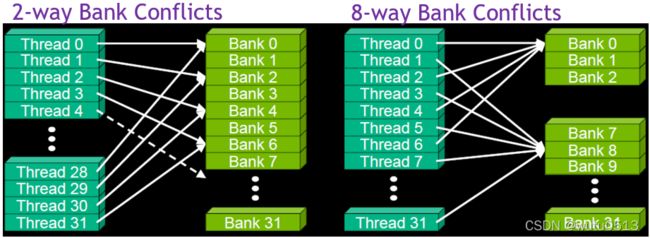
• 什么情况会发生bank conflict
  • 如果同一个 warp 中的线程访问同一个 bank 中的不同地址时将发生 bank conflict。
• 什么情况不会发生bank conflict
  • 广播(broadcast)：当一个 warp 中的所有线程访问同一地址的共享内存时，这是最好的情况
  • 多播(mutilcast)：一个 warp 中的多个线程访问同一个 bank 的同一个地址时（其他线程也没有访问同一个bank 的不同地址），次优
  • 即使同一个 warp 中的线程随机的访问不同的 bank，只要没有访问同一个 bank 的不同地址就不会发生 bank conflict。

No Bank Conflicts

Multi-way Bank Conflicts

并行归约

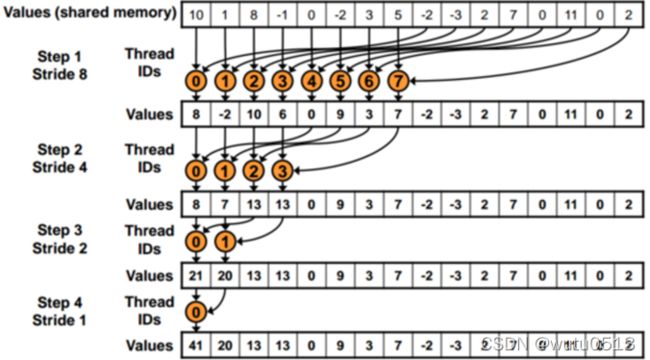
并行归约kernel函数

分支发散版

Each thread block takes 2*BlockDim.x input elements
Each thread loads 2 elements into shared memory

假设warpsize为8，bank数量为8，分析stride = 1时是否有bank conflicts发生 ？
线程4访问的sdata[8]和sdata[9]映射到了bank[0]和bank[1]，
线程0访问的sdata[0]和sdata[1]映射到了bank[0]和bank[1]，
bank conflicts发生！

__shared__ float partialSum[2*BLOCK_SIZE];

unsigned int t = threadIdx.x;
unsigned int start = 2*blockIdx.x*blockDim.x;
partialSum[t] = input[start + t];
partialSum[blockDim + t] = input[start + blockDim.x + t];
for (unsigned int stride = 1; stride <= blockDim.x;  stride *= 2) {
  __syncthreads();
  if (t % stride == 0)
    partialSum[2*t]+= partialSum[2*t+stride];
}

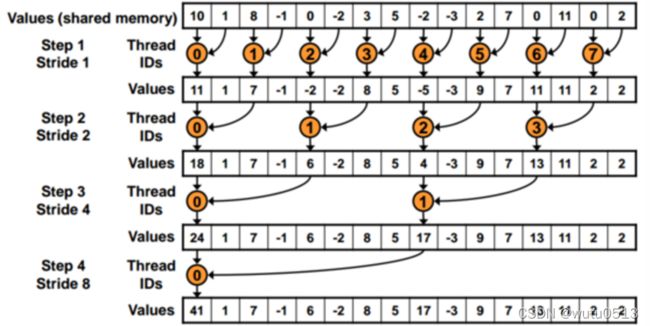
无分支发散版

for (unsigned int stride = blockDim.x; stride > 0;  stride /= 2) {
  __syncthreads();
  if (t < stride)
	  partialSum[t] += partialSum[t+stride];
}

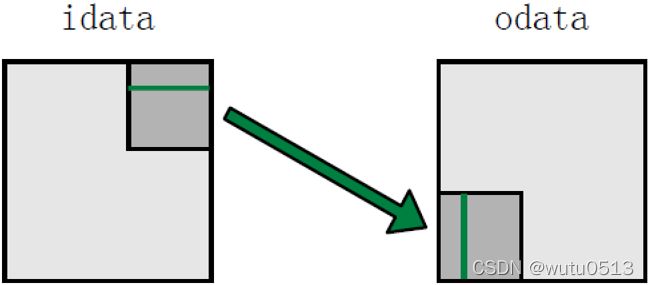
Transpose 矩阵转置

• 每个线程块在矩阵的一个瓦片上操作
• 原始版本存在对global memory按步长访问的情况

原始Transpose

读操作支持合并, 写操作不支持(以宽度为步长)

global_ void transposeNaive(float *odata, float *idata, int width, int height){
    //TILE_DIM = blockDim.x;
	int col = blockIdx.x * TILE_DIM + threadIdx.x ;
	int row = blockIdx.y * TILE_DIM + threadIdx.y ;
    int index_in = col + width * row ;
	int index_out= row + height * col ;
	odata[index_out] = idata[index_in] ;
}

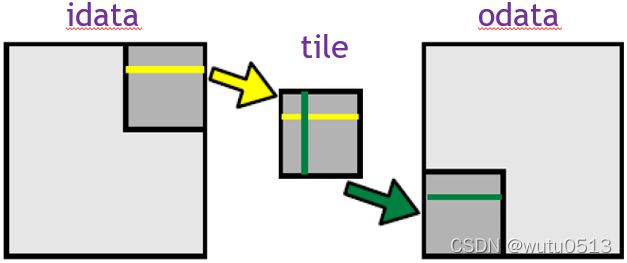
通过shared memory 实现转置(kernel)

先将 warp 的多列元素存入shared memory ，再以连续化的数据写入global memory。
需要同步__syncthreads() 因为需要用到其它线程将global memory的数据存储到shared memory 的数据。

假设warpsize为32，bank数量为32，tile尺寸为32x32，观察是否有bank conflicts发生？
1-列中的数据存于相同的bank
2-读入 warp 一列数据时存在32-way bank conflict

__global__ void transposeCoalesced(float *odata, float *idata, int width, int height){
	__shared__ float tile[TILE_DIM][TILE_DIM];
	int col = blockIdx.x * TILE_DIM + threadIdx.x;
    int row = blockIdx.y * TILE_DIM + threadIdx.y;
    int index_in = col + row * width;
	col = blockIdx.y * TILE_DIM + threadIdx.x;
    row = blockIdx.x * TILE_DIM + threadIdx.y;
    int index_out = col + row * height;
	tile[threadIdx.y][threadIdx.x] = idata[index_in];
    __syncthreads();
	odata[index_out] = tile[threadIdx.x][threadIdx.y];
}

解决方案– 填充shared memory 数组

_shared_ float tile[TILE_DIM][TILE_DIM+1];
反对角线上的数据存于相同的bank

__global__ void transposeCoalesced(float *odata, float *idata, int width, int height){
	__shared__ float tile[TILE_DIM][TILE_DIM + 1];
	int col = blockIdx.x * TILE_DIM + threadIdx.x;
    int row = blockIdx.y * TILE_DIM + threadIdx.y;
    int index_in = col + row * width;
	col = blockIdx.y * TILE_DIM + threadIdx.x;
    row = blockIdx.x * TILE_DIM + threadIdx.y;
    int index_out = col + row * height;
	tile[threadIdx.y][threadIdx.x] = idata[index_in];
    __syncthreads();
	odata[index_out] = tile[threadIdx.x][threadIdx.y];
}

简单调优方法

循环展开

每轮循环包含的指令：一条浮点数乘法 一条浮点数加法
每轮循环包含的其它指令：更新循环计数器
每轮循环包含的其它指令：更新循环计数器 分支
每轮循环包含的其它指令：更新循环计数器 分支 地址运算

指令混合
2 条浮点运算指令
1 条循环分支指令
2 地址运算指令
1 循环计数器自增指令

for (int k = 0; k < BLOCK_SIZE; ++k)
{
     Pvalue += Ms[ty][k] * Ns[k][tx];
}

展开：
不再有循环
不再有循环计数器更新
不再有分支
常量索引– 不再有地址运算

Pvalue +=
    Ms[ty][0] * Ns[0][tx] +
    Ms[ty][1] * Ns[1][tx] +
    ...
    Ms[ty][15] * Ns[15][tx]; //      BLOCK_SIZE = 16

循环展开：自动实现

循环展开有什么缺点? 寄存器的使用量大大上升

#pragma unroll BLOCK_SIZE
for (int k = 0; k < BLOCK_SIZE; ++k)
{
      Pvalue += Ms[ty][k] * Ns[k][tx];
}

并行计算模式(归约)

并行归约

目标

学习并行归约模式

• 重要的并行计算类
• 工作效率分析
• 资源效率分析

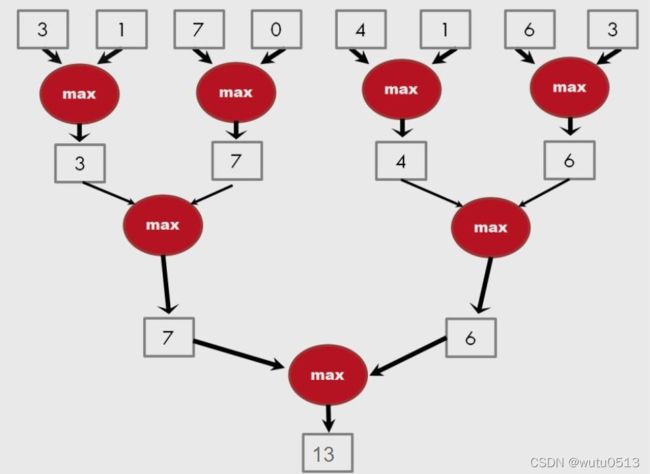
一种并行归约树算法以 log(N) 步执行 N-1 次操作

快速分析

一个基本的归约内核

并行计算模式(scan)

前缀总和 Prefix Sum

目标

掌握并行扫描（前缀和）算法

• 常用于并行工作分配和资源分配
• 许多并行算法中将串行计算转换为并行计算的关键原语
• 一个基本的并行计算模式
• 并行代码 / 算法的工作效率

包含扫描（前缀总和）定义

定义：扫描操作采用一个二元结合运算符 ⊕，以及一个包含 n 个元素的数组，[x0, x1, …, xn-1],

并返回数组 [x0, (x0 ⊕x1), …, (x0 ⊕x1 ⊕… ⊕xn-1)]。

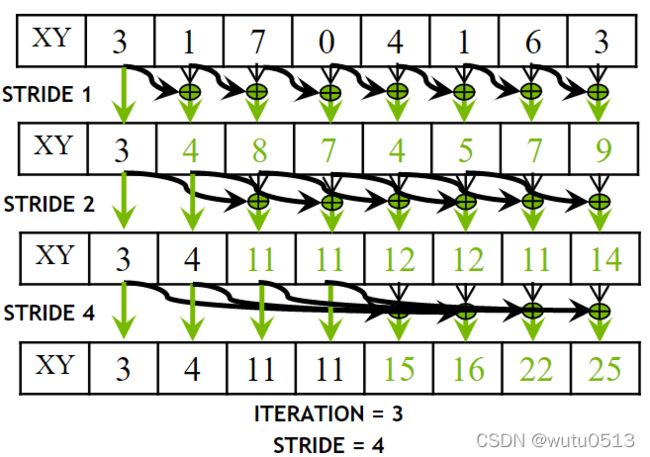
示例：如果⊕是加法，则对数组的扫描操作将返回 [3 1 7 0 4 1 6 3], [3 4 11 11 15 16 22 25]。

包含顺序加法扫描

Given a sequence [x0, x1, x2, … ]
Calculate output [y0, y1, y2, … ]
Such that y0 = x0 y1 = x0 + x1 y2 = x0 + x1+ x2
Using a recursive definition yi = yi − 1 + xi

一个工作效率高的 C 实现

y[0] = x[0];
for (i = 1; i < Max_i; i++) y[i] = y [i-1] + x[i];

工作效率低下的扫描内核

目标

学习编写和分析高性能扫描内核

• 交错归约树
• 线程索引到数据映射
• 屏障同步
• 工作效率分析

一个更好的并行扫描算法

• 从设备读取输入到共享内存
• 迭代 log(n) 次； stride from 1 to n-1: double stride each iteration
• 将输出从共享内存写入设备内存

Kernel

__global__ void work_inefficient_scan_kernel(float *X, float *Y, int InputSize) {
	__shared__ float XY[SECTION_SIZE];
	int i = blockIdx.x * blockDim.x + threadIdx.x;
	if (i < InputSize) {
        XY[threadIdx.x] = X[i];
    }
	// the code below performs iterative scan on XY
	for (unsigned int stride = 1; stride <= threadIdx.x; stride *= 2) {
		__syncthreads();
		float in1 = XY[threadIdx.x - stride];
		__syncthreads();
		XY[threadIdx.x] += in1;
	}
	__ syncthreads();
	if (i < InputSize) {
        Y[i] = XY[threadIdx.x];
    }
}

一个高效的并行扫描内核

目标

学习编写高效的扫描内核

• 两阶段平衡树遍历
• 积极重用中间结果
• 通过更复杂的线程索引到数据索引映射减少控制发散

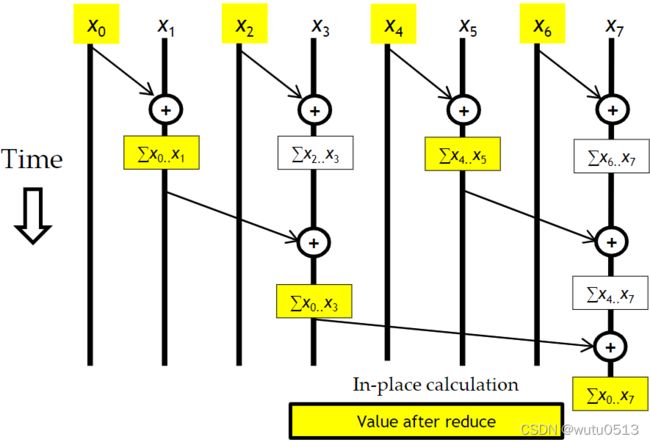
并行扫描 - 归约阶段

// XY[2*BLOCK_SIZE] is in shared memory
for (unsigned int stride = 1;stride <= BLOCK_SIZE; stride *= 2) 
{
	int index = (threadIdx.x+1)*stride*2 - 1;
	if(index < 2*BLOCK_SIZE)
		XY[index] += XY[index-stride];
	__syncthreads();
}

put it together

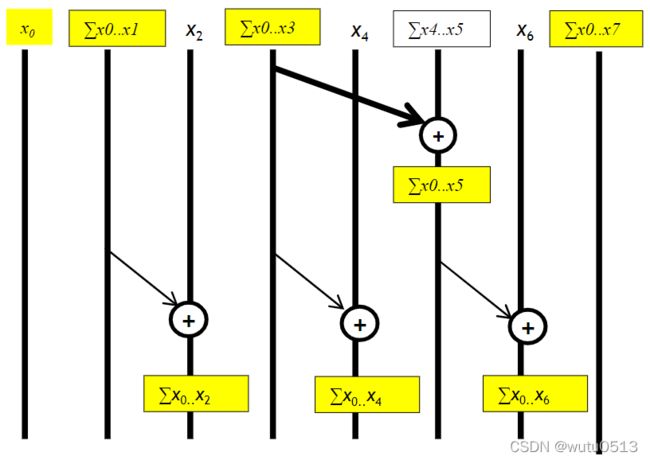
Kernel

for (unsigned int stride = BLOCK_SIZE/2; stride > 0; stride /= 2) {
	__syncthreads();
	int index = (threadIdx.x+1)*stride*2 - 1;
	if(index+stride < 2*BLOCK_SIZE) {
		XY[index + stride] += XY[index];
	}
}
__syncthreads();
if (i < InputSize) 
	Y[i] = XY[threadIdx.x];

题目

第二个模块

1.lf we want to allocate an array of v integer elements inCUDA device global memory, what would be an appropriate expression for the second argument of the cudaMalloc() call?

A n
B v
C n*sizeof(int)
D v*sizeof(int)

正确答案 ：B

2.lf we want to allocate an array of n floating-point elements and have a floating-point pointer variable d_A to point to the allocated memory, what would be an appropriate expression for the first argument of the cudaMalloc() call?

A n
B (void *) d_A
C *d_A
D (void**)&d_A

正确答案 ：D

3.lf we want to copy 3000 bytes of data from host array h_A(_A is a pointer to element 0 of the source array) to device array d_A(_A is a pointer to element 0 of the destination array), what would be an appropriate APl call for this in CUDA?

A cudaMemcpy(3000, h_A, d_A,cudaMemcpyHostToDevice);
B cudaMemcpy(h_A, d_A, 3000,cudaMemcpyDeviceTHost);
C cudaMemcpy(d_A, h_A, 3000,cudaMemcpyHostToDevice);
D cudaMemcpy(3000, d_A, h_A,cudaMemcpyHostToDevice);

正确答案 ：C

4.How would one declare a variable err that can appropriately receive returned value of a CUDA APl call?

A int err;
B cudaError err;
C cudaError_t err;
D cudaSuccess_t err;

正确答案 ：C

A new summer intern was frustrated with CUDA. He has been complaining that CUDA is very tedious: he had to declare many functions that he plans to execute on both the host and the device twice, once as a host function and once as a device function. What is your response?

第三个模块

1 lf we need to use each thread to calculate one output element of a vector addition, what would be the expression for mapping the thread/block indices to data index:

A i=threadldx.x + threadldx.y;
B i=blockldx.x + threadldx.x;
C i=blockldx.x * blockDim.x + threadldx.x;
D i=blockldx.x * threadldx.x;

正确答案 ：C

2 We want to use each thread to calculate two (adjacent) output elements of a vector addition. Assume that variable i should be the index for the first element to be processed by a thread.What would be the expression for mapping the thread/block indices to data index of the first element?

A i = blockldx.x*blockDim.x + threadldx.x+2;
B i = blockldx.x*threadldx.x*2
C i = (blockldx.x*blockDim.x +threadldx.x)*2
D i = blockldx.x*blockDim.x*2 +threadldx.x

正确答案 ：C

3 We want to use each thread to calculate two output elements of a vector addition. Each thread block processes 2*blockDim.x consecutive elements that form two sections. All threads in each block will first process a section,each processing one element. They will then all move to the next section, again each processing one element. Assume that variable i should be the index for the first element to be processed by a thread. What would be the expression for mapping the thread/block indices to data index of the first element?

A i = blockldx.x*blockDim.x + threadldx.x + 2;
B i = blockldx.x*threadldx.x*2
C i = (blockldx.x*blockDim.x +threadldx.x)*2
D i = blockldx.x*blockDim.x*2 +threadldx.x

正确答案 ：D

4 For a vector addition, assume that the vector length is 8000, each thread calculates one output element, and the thread blocksize is 1024 threads. The programmer configures the kernel launch to have a minimal number of thread blocks to cover all output elements. How many threads will be in the grid?

A 8000
B 8196
C 8192
D 8200

正确答案 ：C

5 已知费米架构(英伟达显卡架构之一）下每个SM能接收1536 threads，每一个SM能接收 8 Blocks。下面能使SM利用率达到100%的配置是（)

A int threadPerBlock=128;
B int threadPerBlock=256;
C int threadPerBlock=512;
D int threadPerBlock=1024;

正确答案 ：BC

6 已知开普勒架构（英伟达显卡架构之一）下每个SM能接收2048 threads，每一个SM能接收 16 Blocks。下面能使SM利用率达到100%的配置是（)

A int threadPerBlock=128;
B int threadPerBlock=256;
C int threadPerBlock=512;
D int threadPerBlock=1024;

正确答案 ：ABCD

第四个模块

1 Assume that a kernel is launched with 1000 thread blocks each of which has 512 threads. lf a variable is declared as a shared memory variable, how many versions of the variable will be created through the lifetime of the execution of the kernel?

A 1;
B 1,000
C 512
D 512,000

正确答案 ：B

第五个模块

1 We are to process a 600x800 (800 pixels in the x or horizontal direction, 600 pixels in the y or vertical direction) picture with the PictureKernel(). That is m’ s value is 600 and n’s value is 800.

__global__ void PictureKernel(float* d_Pin, float* d_Pout, int n, int m) {
	//Calculate the row # of the d_Pin and d_Pout element to process
    int Row = blockldx.y*blockDim.y + threadldx.y;
	// Calculate the column # of the d_Pin and d_Pout element to process
	int Col = blockldx.x*blockDim.x + threadldx.x;
	//each thread computes one element of d_Pout if in range
	if ((Row < m)&&(Col < n)) {
		d_Pout[Row*n+Col]= 2*d_Pin[Row*n+Col];
    }
}

Assume that we decided to use a grid of 16X16 blocks. That is, each block is organized as a 2D
16X16 array of threads. How many warps will be generated during the execution of the kernel?

A 37*16
B 38*50
C 38*8*50
D 38*50*2

正确答案 ：C

2 In Question 1, how many warps will have control divergence?

A 37 +50*8
B 38*16
C 50
D 0

正确答案 ：D

3 In Question 1, if we are to process an 800x600 picture (600 pixels in the x or horizontal direction and 800 pixels in the y or vertical direction) picture, how many warps will have control divergence?

A 37 + 50*8
B 38*16
C 50*8
D 0

正确答案 ：C

4 In Question 1, if are to process a 799x600 picture (600 pixels in the x direction and 799 pixels in the y direction), how many warps will have control divergence?

A 37 + 50*8
B (37 + 50)*8
C 50*8
D 0

正确答案 ：A

第六个模块

1 Assume that we want to use each thread to calculate two (adjacent) output elements of avector addition. Assume that variable i shouldbe initialized with the index for the first element to be processed by a thread. Which of the following should be used for such initialization to allow correct, coalesced memory accesses to these first elements in the following statement? if(i < n) C[i] = A[i]+ B[i];

A int i=(blockldx.x*blockDim.x)*2 +threadldx.x;
B int i=(blockldx.x*blockDim.x +threadldx.x)*2;
C int i=(threadldx.x*blockDim.x)*2 +blockldx.x;
D int i=(threadldx.x*blockDim.x +blockldx.x)*2;

正确答案 ：A

2 Continuing from Question 1, what would be the correct statement for each thread to process the second element?

A lf (i B lf (i+1 C lf (i+threadldx.x < n) C[i+threadldx.x]=A[i+threadldx.x]+ B[i+threadldx.x];
D if(i+blockDim.x < n) C[i+blockDim.x]=A[i+blockDim.x] + B[i+ blockDim.x];

正确答案 ：D

3 Assumethefollowing simple matrix multiplication kernel

global__ void MatrixMulKernel(float* M, float* N,float* P, int Width){
    int Row = blockldx.y*blockDim.y+threadldx.y;
    int Col = blockldx.x*blockDim.x+threadldx.x;
    if ((Row < Width)&&(Col < Width)){
        float Pvalue = O;
        for (int k = O; k < Width; ++k){
            Pvalue += M[Row*Width+k]*N[k*Width+Col];
        }
        P[Row*Width+Col]= Pvalue;
    }
}

Based on the judging criterion in Lecture 6.2, which of the following is true?

A M[Row*Width+k] and N[k*Width+Col] arecoalesced but P[Row*Width+Col] is not
B M[Row*Width+k],N[k*Width+Col] andP[Row*Width+Col] are all coalesced
C M[Row*Width+k] is not coalesced but N[k*Width+Col] and P[Row*Width+Col]both are
D M[Row*Width+k] is coalesced but N[k*Width+Col] andt P[Row*Width+Col] are not

正确答案 ：C

4 For the tiled single-precision matrix multiplication kernel in question 3, assume that each thread block is 32×32 and the system has a DRAM bust size of 128 bytes. How many DRAM bursts will be delivered to the processor as a result of loading one A-matrix element by a thread block (one k step)? Keep in mind that each single precision floating point number is four bytes.

A 16
B 32
C 64
D 128

正确答案 ：B
解释：128/4 = 32

第七个模块

1 Assume that each atomic operation in a DRAM system has a total latency of 100ns. What is the maximal throughput we can get for atomic operations on the same global memory variable?

A 100G atomic operations per second
B 1G atomic operations per second
C 0.01G atomic operations per second
D 0.0001G atomic operations per second

正确答案 ：C

2 For a processor that supports atomic operations in L2 cache, assume that each atomic operation takes 4ns to complete in L2 cache and 100ns to complete in DRAM. Assume that 90% of the atomic operations hit in L2 cache. What is the approximate throughput foratomic operations on the same global memory variable?

A 0.225G atomic operations per second
B 2.75G atomic operations per second
C 0.0735G atomic operations per second
D 100G atomic operations per second

正确答案 ：C

3 In question 1, assume that a kernel performs 5 floating-point operations per atomic operation. What is the maximal floating-point throughput of the kernel execution as limited by the throughput of the atomic operations?

A 500 GFLOPS
B 5 GFLOPS
C 0.05 GFLOPS
D 0.0005 GFLOPS

正确答案 ：C

4 In Question 1, assume that we privatize the global memory variable into shared memory variables in the kernel and the shared memory access latency is 1ns.All original global memory atomic operations are converted into shared memory atomic operation.For simplicity, assume that the additional global memory atomic operations for accumulating privatized variable into the global variable adds 10% to the total execution time. Assume that a kernel performs 5 floating-point operations per atomic operation. What is the maximal floating-point throughput of the kernel execution as limited by the throughput of the atomic operations?

A 4500 GFLOPS
B 45 GFLOPS
C 4.5 GFLOPS
D 0.45 GFLOPS

正确答案 ：C

5 To perform an atomic add operation to add the value of an integer variable Partial to a global memory integer variable Total. Which one of the following statements should be used?

A atomicAdd(Total, 1);
B atomicAdd(&Total,&Partial);
C atomicAdd(Total, &Partial);
D atomicAdd(&Total,Partial);

正确答案 ：D