也谈特征值和特征向量的几何意义

在当前的大数据分析时代，数据降维是一个重要的分析技术。而谈到数据降维，就离不开一门最为抽象难懂的数学学科分支——线性代数。有人可能会问：一堆向量和矩阵符号的线性代数到底有鸟用？简单地不科学地说，线性代数就是一门让m维世界和n维世界相互交互的科学。

古希腊著名的哲学家阿基米德曾经说：“给我一个支点，我能撬动地球。”

在元宇宙盛行的新时代，有这样一坨做保险数据分析的精算师说：“给我一个矩阵，我能把n维的元宇宙变为一条线.” （ “线”性代数高手中的网络用语： 看我来 “秒线” 一切？   ：）

开个玩笑后，开始说正事。今天想聊的是数据降维或者说线性代数绕不开的两个名词——特征值和特征向量。看到CSDN里有很多解释特征值和特征向量的帖子，有些提到了他们的几何意义，但是看完之后，感觉大多数的帖子写的都太学术了，让新手看得云里雾里。所以，今天我也从一个保险精算师的角度，谈谈特征值和特征向量的几何解释，希望我的解释，能让更多的新人理解。

为了说明问题的实质，直接上一个简单的例子，数据也会设计的尽量简单。我会尽量避免教科书式的公式，为了不让新人看着那些公式越看越迷糊。

有这样一个矩阵：

这里先把它的特征值和特征向量给出来：它有两个特征值，一个是5，对应的一个特征向量是（3，1）；另一个特征值是-2，对应的一个特征向量是（1，-2）。（PS：特征值和特征向量都很重要，但是从某种意义上讲，特征向量更重要，它重塑了一个变型的坐标系）

下面，开始说重点的东西，也就是特征值和特征向量的几何意义。

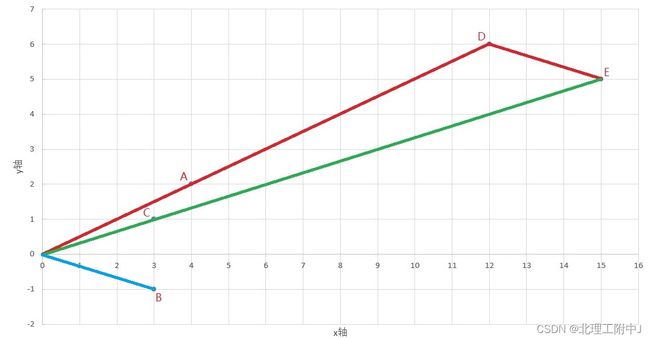
我们将上面那个矩阵的2个列向量，（4，2）和（3，-1）作为A点和B点画在坐标系里。

然后，我们以特征值5对应的那个特征向量（3，1）作为C点，也画在坐标系里。（PS：这里仅以特征值5为例，来做解释。另一个特征值-2，如果有人想解释，可以自己试一试）

先画出上面的坐标图像，下面开始解释。

注意特征值5对应的那个特征向量（3，1），它的使用方法是，将坐标图中的向量OA变为3倍，也就是到达了点D。随后，在D点的基础上，再加上1倍的向量OB，也就是从D点到达了E点。(PS: 其实这是一种在变了形的坐标系里的点(3,1)的映射点，在这个变了形的坐标系里，x轴的单位向量不再是(1,0) 而是(4,2), y轴的单位向量不再是(0,1)而是(3,-1)，专业术语叫做坐标系的基变换 ）

我们看看原点O、点C、点E有什么特性？看到了吧，3点共线。

而且不仅是3点共线，OE的长度是OC长度的5倍。这个5倍是什么东西？其实就是矩阵的特征值5.

看懂了这个例子以后，希望你再深刻体会一下下面这个比较抽象的自然段语言：

“ 在线性代数里，矩阵乘法对应了一个变换，是把任意一个向量变成另一个方向或长度不同的新向量。在这个变换的过程中，原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换，不对这些向量产生旋转的效果，那么这些向量就称为这个矩阵的特征向量，伸缩的比例就是特征值。”

在这段话里，有2个句号。第一句，提到了矩阵乘法就是从旋转和伸缩，我在此前的CSDN博客文章中已经说过这个道理。然后就是第二句话，就是今天谈的东西。

在我们的例子中，那个矩阵 [ [4,3], [2,-1] ]对特征向量OC，也就是从O点到C(3，1)，只使向量发生了伸缩（具体是伸长了5倍，也就是特征值），而不对向量产生旋转的效果。You must see it.

不旋转，是很关键的一件事。从数据降维的角度讲，我们将本来是在2维的坐标系里又伸长、又旋转的一个复杂的工作，改变为在一个1维的坐标轴OC上把它直接伸长5倍就ok了。

明白了这个道理，我相信你就明白了特征值和特征向量的几何意义。其实，像主成分分析、因子分析这些主要的数据降维技术，都是采用了相同的思路，所以这些降维技术在疯狂使用特征值和特征向量这些东西。

实际上，在工作中，我能看到很多新人根据他们在学校所学，都能够完成相应的工作，学校教了他们 how to do，但是，能够 真正理解 why to do 的新人其实挺少的。希望此文能够让更多的新人，理解 how to do 背后的东西。