m基于EM参数估计的Gamma随机过程电池剩余寿命预测matlab仿真

目录

1.算法描述

2.仿真效果预览

3.MATLAB核心程序

4.完整MATLAB

---

1.算法描述

       近年来，为了应对传统化石燃料枯竭和环境恶化，锂离子电池在新能源汽车和电网储能等领域取得了广泛应用。然而，锂离子电池在使用过程中的性能衰减是关键技术难点，制约了电池的剩余使用寿命（Remaining useful life, RUL）。锂离子电池是一个复杂的电化学系统，在工作过程中会产生SEI膜增长、析锂和电解液氧化等副反应。电池副反应将导致电池的性能衰减，从宏观上表现为容量减少和内阻增加，从而降低了电池的使用寿命。准确预测锂离子电池在不同使用条件下的剩余使用寿命不仅能保证系统的安全可靠运行，并且能实现电池剩余价值的最大化利用。因此剩余寿命预测对于电池管理和梯次利用至关重要,本文将为锂离子电池的剩余寿命预测技术提供有力支撑。

EM参数估计

       EM算法算是机器学习中有些难度的算法之一，也是非常重要的算法，曾经被誉为10大数据挖掘算法之一，从标题可以看出，EM专治带有隐变量的参数估计，我们熟悉的MLE(最大似然估计)一般会用于不含有隐变量的参数估计，应用场景不同。

       最大期望算法（Expectation-maximization algorithm，又译期望最大化算法）在统计中被用于寻找，依赖于不可观察的隐性变量的概率模型中，参数的最大似然估计。在统计计算中，最大期望（EM）算法是在概率模型中寻找参数最大似然估计或者最大后验估计的算法，其中概率模型依赖于无法观测的隐性变量。最大期望算法经常用在机器学习和计算机视觉的数据聚类（Data Clustering）领域。为了同时估计参数和隐藏状态，将期望最大化（EM）与扩展卡尔曼滤波和平滑结合在一起，其目的是对未知隐藏状态的不确定估计进行积分，并根据给定的观测数据优化参数的边际似然性。通过使用扩展卡尔曼滤波和平滑算法，可以实现对后验分布更精确的估计。

Gamma随机过程

       伽马过程（Gamma Process）是随机过程理论中一类重要过程Lévy过程的一种，其增量服从独立的gamma分布，可以用于描述单调递增的变化过程，属于Lévy subordinator中的一种,gamma过程，通常记作，由两个正参数决定，其中称为形状参数，控制了跳跃点到达的频率，称为尺度参数，控制了跳跃的跃度。同时，该过程假设在时刻t=0时，其值为0，即在初始时刻位置在原点。

        使用伽马函数定义了许多概率分布，例如伽马分布，Beta分布，狄利克雷分布，卡方分布和学生t分布等。 对于数据科学家，机器学习工程师，研究人员来说，伽马函数可能是一种最广泛使用的函数，因为它已在许多分布中使用。然后将这些分布用于贝叶斯推理，随机过程（例如排队模型），生成统计模型（例如潜在狄利克雷分配）和变分推理。

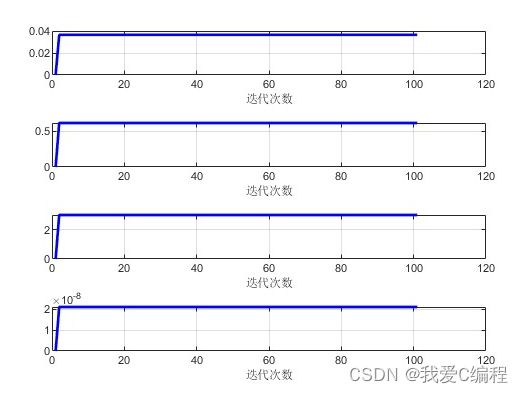
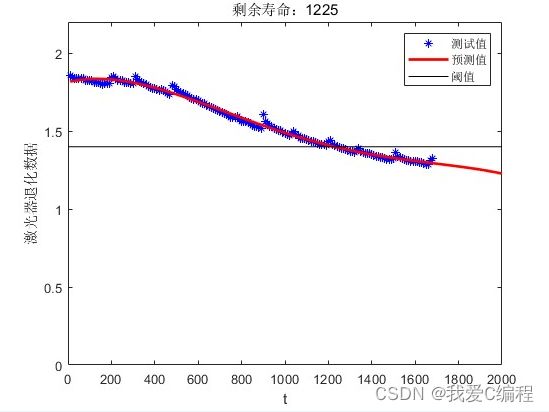
2.仿真效果预览

matlab2022a仿真结果如下：

 

3.MATLAB核心程序

............................................................
 
for i = 1:Iter
    i
    ykt  = yk;
    ykt1 = [0,yk(1:end-1)];
    xkt  = xk;
    xkt1 = [0,xk(1:end-1)];
    
    %粒子滤波
    if i == 1
       [Exk,Ws]   = func_Particlefilter(ykt,xkt,c0,delta0);
       [Exk1,Ws]  = func_Particlefilter(xkt1,ykt1,c0,delta0);
       [Exklog,Ws]= func_Particlefilter(log(xk_xk1),ykt1,c0,delta0);
    else
       [Exk,Ws]   = func_Particlefilter(ykt,xkt,c_(i-1),delta_(i-1));
       [Exk1,Ws]  = func_Particlefilter(xkt1,ykt1,c_(i-1),delta_(i-1));
       [Exklog,Ws]= func_Particlefilter(log(xk_xk1),log(ykt1),c_(i-1),delta_(i-1));
    end
 
    %E步骤
    if i == 1
       E1    = sum(a0*dt*log(epls0) - log(gamma(a0*dt))+(a0*dt-1)*Exklog-epls0*(Exk-Exk1));
       E2    = sum(-log(delta0)-0.5*log(2*pi)-1/(2*delta0^2)*(yk.^2-2*yk.*c0.*Exk+c0^2.*Exk.^2));
       theta = E1+E2;
    else
       E1    = sum(a_(i)*dt*log(epls_(i)) - log(gamma(a_(i)*dt))+(a_(i)*dt-1)*mean(log(xk_xk1))-epls_(i)*(Exk-Exk1));
       E2    = sum(-log(delta_(i-1))-0.5*log(2*pi)-1/(2*delta_(i-1)^2)*(yk.^2-2*yk.*c_(i-1).*Exk+c_(i-1)^2.*Exk.^2));
       theta = E1+E2;
    end
    
    %M步骤
    if i == 1
       a        = Exk(end)/t(end);
       epls     = a*t(end)/max(Exk(end),1);
    else
       a        = Exk(end)/t(end);
       epls     = a*t(end)/max(Exk(end),1);
    end
    c        = sum(yk.*Exk)./sum(Exk.^2);
    delta    = sqrt(1/n*sum(yk.^2 - 2*yk.*c.*Exk + c^2.*Exk.^2));
    a_(i+1)    = a;
    epls_(i+1) = epls;
    c_(i+1)    = c;
    delta_(i+1)= delta;
end
 
................................................
figure;
idx=0;
for jj = sers
    idx=idx+1;
    a_s    = jj*a_;
    for j = 1:length(tr)
        F_tmps = [];
        for s = 1:length(xc)
            F_tmps(s) = func_gamma(xc(s),a_s(end)*tr(j),(D-xc(s))/epls_(end))/gamma(a_s(end)*tr(j));
        end
        F(j) = mean(F_tmps)/(sers(end)-jj)^0.5;
    end 
    f=abs(F);
    plot3(400*tr,(jj)*ones(size(tr)),f,'k','linewidth',1);
    [V,I] = max(f);
    hold on
    xx(idx)  = 400*tr(I);
    yy(idx)  = (jj);
    ff{idx}  = f;
end
plot3(xx(1:end-1),yy(1:end-1),0*ones(size(xx(1:end-1))),'m-s','linewidth',1);
 
xlabel('剩余寿命');
ylabel('检测时间');
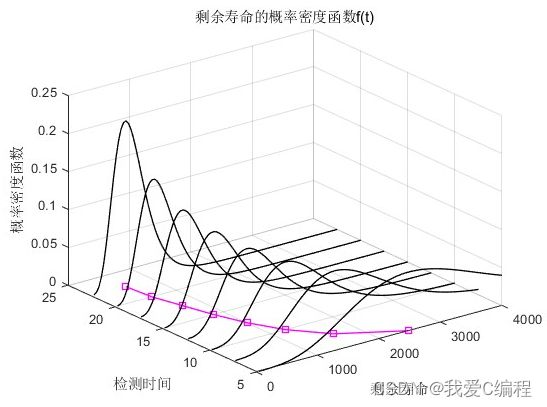
zlabel('概率密度函数');
title('剩余寿命的概率密度函数f(t)');
grid on
01_187m

4.完整MATLAB

V