【机器学习-周志华】学习笔记-第十六章
记录第一遍没看懂的
记录觉得有用的
其他章节:
第一章
第三章
第五章
第六章
第七章
第八章
第九章
第十章
十一章
十二章
十三章
十四章
十五章
十六章
强化学习任务通常用马尔可夫决策过程来描述:机器处于环境 E E E中,状态空间为 X X X,其中每个状态 x ∈ X x \in X x∈X是机器感知到的环境的描述;机器能采取的动作构成了动作空间 A A A;若某个动作 a ∈ A a \in A a∈A用在当前状态 x x x上,则潜在的转移函数 P P P将使得环境从当前状态按某种概率转移到另一个状态;在转移到另一个状态的同时,环境会根据潜在的奖赏函数 R R R反馈给机器一个奖赏。

机器要做的是通过在环境中不断地尝试而学得一个"策略" π \pi π,根据这个策略,在状态 x x x下就能得知要执行的动作 a = π ( x ) a=\pi(x) a=π(x)
K-摇臂赌博机
K-摇臂赌博机是最简单的强化学习模型,当前的收益仅跟当前的选择有关。
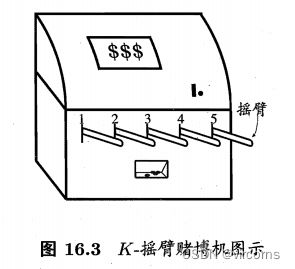
若仅为获知每个摇臂的期望奖赏,则可采用"仅探索“法:将所有的尝试机会平均分配给每个摇臂(即轮流按下每个摇臂),最后以每个摇臂各自的平均吐币橄率作为其奖赏期望的近似估计。若仅为执行奖赏最大的动作,则可采用"仅利用” 法:按下目前最优的(即到目前为止平均奖赏最大的)摇臂,若有多个摇臂同为最优,则从中随机选取一个。
事实上,“探索"和"利用” 这两者是矛盾的,因为尝试次数有限,加强了一方则会自然削弱另一方,这就是强化学习所面临的"探索-利用窘境" 。 显然,欲累积奖赏最大,则必须在探索与利用之间达成较好的折中。
ϵ \epsilon ϵ-贪心法
ϵ − 贪心 \epsilon-贪心 ϵ−贪心法::每次尝试时,以 ϵ \epsilon ϵ的概率进行探索,即以均匀概率随机选取一个摇臂;以 1 − ϵ 1-\epsilon 1−ϵ的概率进行利用,即选择当前平均奖赏最高的摇臂。
若摇臂 k k k被尝试了 n n n次,得到的奖赏为 v 1 , v 2 , . . . , v n v_1,v_2,...,v_n v1,v2,...,vn,则平均奖赏: Q ( k ) = 1 n ∑ i = 1 n v i Q(k)=\frac{1}{n}\sum_{i=1}^n v_i Q(k)=n1∑i=1nvi。为了更高效的记录,尝试对均值进行增量式计算,用下标表示尝试的次数,则经过第 n n n次尝试获得奖赏 v n v_n vn后,平均奖赏为: Q n ( k ) = 1 n ( ( n − 1 ) ∗ Q n − 1 ( k ) + v n ) = Q n − 1 ( k ) + 1 n ( v n − Q n − 1 ( k ) ) Q_n(k)=\frac{1}{n}((n-1)*Q_{n-1}(k)+v_n)=Q_{n-1}(k)+\frac{1}{n}(v_n-Q_{n-1}(k)) Qn(k)=n1((n−1)∗Qn−1(k)+vn)=Qn−1(k)+n1(vn−Qn−1(k))
ϵ \epsilon ϵ-贪心算法伪代码如下:一共尝试 T T T次,选取随机数,如果小于 ϵ \epsilon ϵ就探索,否则就利用

Softmax
Softmax算法基于当前已知的摇臂平均奖赏来对探索和利用进行折中。若各摇臂的平均奖赏相当,则选取各摇臂的概率也相当;若某些摇臂的平均奖赏明显高于其他摇臂,则它们被选取的概率也明显更高。
Softmax算法描述如下:其中 τ > 0 \tau>0 τ>0称为“温度”, τ \tau τ越小则平均奖赏高的摇臂被选取的概率越高。 τ \tau τ趋于0时则算法趋于“仅利用”, τ \tau τ趋于无穷大则算法趋于“仅探索”。

有模型学习
若 E = < X , A , P , R > E=
策略评估就是通过递归求该策略的累计奖赏,然后进行值的更新。获得状态值函数后,即可根据公式计算出状态-动作值函数。策略评估算法如下:

对某个策略的累积奖赏进行评估后,若发现它并非最优策略,则当然希望对其进行改进。理想的策略应能最大化累积奖赏如下图,也就是说,对所有状态的 V ( x ) V(x) V(x)求和,求和后最大的那个策略,就是最优策略。

下面就是如何改进至获得最优策略。有两种方法:策略迭代和值迭代。
策略迭代的思路是:首先,随机初始化策略 π \pi π,根据策略去计算状态值函数 V ( x ) V(x) V(x),然后根据状态值函数 V ( x ) V(x) V(x)计算状态-动作值函数 Q ( x , a ) Q(x,a) Q(x,a),再根据状态-动作值函数生成新的策略KaTeX parse error: Expected group after '^' at position 4: \pi^̲',最后令KaTeX parse error: Expected group after '^' at position 8: \pi=\pi^̲',再去计算 V ( x ) V(x) V(x)。由于 Q Q Q在 x x x时,执行的是 a a a动作以后的累积奖赏,而不是当前状态 x x x的累积奖赏,也就是比 V V V多考虑了一步,因此生成的策略更好。
值迭代则基于递推方程,不断迭代直到收敛。
免模型学习
若学习算法不依赖于环境建模,则称为“免模型学习”
蒙特卡罗强化学习
在模型未知的情形下,一个直接的想法就是对环境进行采样。从起始状态出发,使用某种策略进行采样,执行该策略 T T T步并获得轨迹 < x 0 , a 0 , r 1 , x 1 , a 1 , r 2 , . . . , x T − 1 , a T − 1 , r T , x T >
但这样有个问题,就是策略 π \pi π不能是确定性的策略,因为这样每次采样都会得到同样的序列。因此要使用 ϵ \epsilon ϵ-贪心法,以 ϵ \epsilon ϵ的概率随机选择动作,以 1 − ϵ 1-\epsilon 1−ϵ的概率选取当前最优动作。
这样是对 Q Q Q进行了评估,还要对策略 π \pi π进行改进。与有模型学习类似,可以在每轮迭代时,使用当前 Q Q Q值计算最优动作,即可以用同样的方法进行策略改进。
通过上面过程得到的最终策略是一个 ϵ \epsilon ϵ-贪心策略,也就是说,评估和改进的是同一个策略,这也称为“同策略”方法。
同样的,还可以两个策略不同,也就是“异策略”。通过重要性采样(基于一个分布的采样来估计另一个分布下的期望)来实现。
时序差分学习
蒙特卡罗强化学习算法需在完成一个采样轨迹后再更新策略的值估计,但事实上可以每执行一步策略后就进行值函数更新,这就是时序差分学习的思想。
将同策略的蒙特卡洛强化学习修改为增量式,就得到了SARSA算法。将异策略的蒙特卡洛强化学习修改为增量式,就得到了Q-Learning算法。
值函数近似
值函数能表示为一个数组,输入i对应的函数值就是数组元素i的值,且更改一个状态上的值不会影响其他状态上的值。面临无穷多个状态,考虑直接对连续状态空间的值函数进行学习:考虑简单情形,即值函数能表达为状态的线性函数: V θ ( x ) = θ T x V_\theta (x)=\theta^T x Vθ(x)=θTx。由于此时的值函数难以像有限状态那样精确记录每个状态的值,因此这样值函数的求解被称为值函数近似。
为了尽可能近似真实值函数,近似程度常用最小二乘误差来度量;为了使误差最小化,采用梯度下降法,对误差求负导数,得到对于单个样本的更新规则:
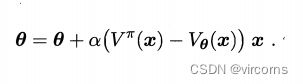
借助时序差分学习,用当前估计的值函数代替真实值函数:
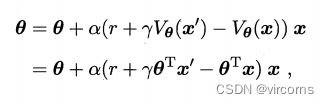
模仿学习
直接模仿学习
强化学习任务中多步决策的搜索空间巨大,基于累积奖赏来学习很多步之前的合适决策非常困难,而直接模仿人类专家的“状态-动作对”可显著缓解这一困难,我们称其为“直接模仿学习”
逆强化学习
在很多任务中,设计奖赏函数往往相当困难,从人类专家提供的范例数据中反推出奖赏函数有助于解决该问题,这就是逆强化学习。.逆强化学习的基本思想是:我们要寻找某种奖赏函数使得范例数据是最优的,然后即可使用这个奖赏函数来训练强化学习策略。
一个较好的办法是从随机策略开始,迭代地求解更好的奖赏函数,基于奖赏函数获得更好的策略,直至最终获得最符合范例轨迹数据集的奖赏函数和策略。