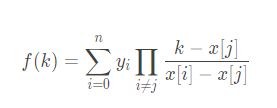拉格朗日插值 学习
前置知识
1 + 1 == 2
内容
拉格朗日插值是用来解决对于给定的n+1个点值,确定一个函数f(),使其能够经过这n+1个点,且f()是n次多项式,同时,对于一个给定的点x,它可以快速求出f(x)的值,即使x很大
做法:
以上为普通拉格朗日插值
重心拉格朗日插值:
这种插值主要用来解决动态加点的问题,其实考虑优化上面这个式子
令 w = ∏ i = 0 n k − x [ i ] w = \prod_{i=0}^{n} k - x[i] w=∏i=0nk−x[i] , 同时 p i = ∏ j = 1 j ! = i x [ i ] − x [ j ] p_{i} = \prod_{j=1}^{j!=i}x[i]-x[j] pi=∏j=1j!=ix[i]−x[j]
则 f ( k ) = ∑ i = 0 n y [ i ] ∗ w ( k − x [ i ] ) ∗ p [ i ] f(k) = \sum_{i=0}^{n} \frac{y[i] * w }{(k-x[i])*p[i]} f(k)=∑i=0n(k−x[i])∗p[i]y[i]∗w
其中w是可以预处理O(N)的,同时动态加点维护w可以,那么对于 p i p_{i} pi是可以动态维护的
于是就做完了
贴一道板题:拉格朗日插值
x[i]连续的拉格朗日插值
如果发现x[i]是连续的,那么其实是可以O(N)完成的
具体做法就是令 p r e i = ∏ j = 0 j < = i k − x [ j ] pre_{i} = \prod_{j=0}^{j<=i} k - x[j] prei=∏j=0j<=ik−x[j] , s u f i = ∏ j = n j > = i k − x [ j ] suf_{i} = \prod_{j=n}^{j>=i} k - x[j] sufi=∏j=nj>=ik−x[j]
再记录一个jc[]阶乘数组
那么答案就变成了 a n s = ∑ i = 0 n y i p r e i − 1 ∗ s u f i + 1 j c [ i ] ∗ j c [ n − i ] ∗ ( − 1 ) n − i ans = \sum_{i=0}^{n} y_{i} \frac{pre_{i-1}*suf_{i+1}}{jc[i] *jc[n-i] * (-1)^{n-i}} ans=∑i=0nyijc[i]∗jc[n−i]∗(−1)n−iprei−1∗sufi+1
就完成了
这也有一道例题:CF622F
比较经典的,求自然数幂的和
其实如果令 f x = ∑ i = 1 x i k f_{x} = \sum_{i=1}^{x} i^{k} fx=∑i=1xik
这个东西是k+1次多项式形式的,可以用差分数列来证明
简单来说有一个定理如果数列 {a} 的p 阶差数列是一个非0常数数列,那么称它为p阶等差数列,p阶差数列是指对这个数列做p次差分,如果一个函数g(k)能被写成多项式形式,而每做一次差分,多项式最高次项就会减1,那么如果做了p次发现这变成了一个常数数列,那么他就是一个p解等差数列而 f x f_{x} fx就可以用这样的方式证明
然后如果发现这是一个k+1次多项式形式的,就可以直接上了,时间复杂度为O(Nlogn)的
using namespace std;
const int MAXN = 1e6 + 7;
const int mod = 1e9 + 7;
int n , k;
int pre[MAXN] , jc[MAXN] , suf[MAXN] , f[MAXN];
int mul( int x , int y ){
return 1ll * x * y % mod;
}
int add( int x ){
return x >= mod ? x - mod : x;
}
int qpow( int x , int y ){
int sum = 1;
while( y ){
if( y & 1 ) sum = mul( sum , x );
x = mul( x , x );
y >>= 1;
}
return sum;
}
int main(){
scanf( "%d%d" , &n , &k );
pre[0] = 1;jc[0] = 1;
for( int i = 1 ; i <= k + 2 ; i ++ ){
int t = qpow( i , k );
f[i] = add( f[i-1] + t );
pre[i] = mul( pre[i-1] , n - i + mod );
jc[i] = mul( jc[i-1] , i );
}
suf[k+3] = 1;
for( int i = k + 2 ; i >= 1 ; i -- ){
suf[i] = mul( suf[i+1] , n - i + mod );
}
int ans = 0;
for( int i = 1 ; i <= k + 2 ; i ++ ){
int s = mul( jc[i-1] , jc[k+2-i] );
int tot = mul( mul( f[i] , mul( pre[i-1] , suf[i+1] ) ) , qpow( s , mod - 2 ) );
if( ( k + 2 - i ) & 1 ) tot = add( mod - tot );
ans = add( ans + tot );
}
printf( "%d" , ans );
return 0;
}
因为要先处理前k+2个点来确定多项式,所以时间复杂度要带log
拓展
如果要强行优化到O(N)那么应该怎样办呢?
其实也是可以做的,这个log是带在快速幂上,阶乘逆元是可以递推的,那么有什么方法可以直接算出 x k x^{k} xk呢,这里就要用一个神奇的东西,就是欧拉筛,因为1-k的质数个数是只有 n l o g n \frac{n}{logn} lognn的,那么就可以直接暴力快速幂,而对于合数在筛它的时候直接乘起来即可
这样就成功做到了O(N)了
#include
using namespace std;
const int MAXN = 3e6 + 7;
int n , k , mod;
int pre[MAXN] , jc, suf[MAXN] , f[MAXN] , nic[MAXN];
inline char GetChar(){
static char buf[100001],*p1=buf,*p2=buf;
return p1==p2&&(p2=(p1=buf)+fread(buf,1,100001,stdin),p1==p2)?EOF:*p1++;
}
inline void Read(int &n){
short f=1;
long long x=0;
char c=GetChar();
while(c<'0' || c>'9'){
if(c=='-'){
f=-1;
}
c=GetChar();
}
while(c >= '0' && c <= '9' ){
x=((x<<3)+(x<<1)+(c^48));
c=GetChar();
}
n=x*f;
}
int mul( int x , int y ){
return 1ll * x * y % mod;
}
int add( int x ){
return x >= mod ? x - mod : x;
}
int qpow( int x , int y ){
int sum = 1;
while( y ){
if( y & 1 ) sum = mul( sum , x );
x = mul( x , x );
y >>= 1;
}
return sum;
}
char ss[MAXN];
int prime[MAXN] , ncnt;
bool flag[MAXN];
void getf(){
f[1] = 1 , f[0] = 0;
for( int i = 2 ; i <= k + 3 ; i ++ ){
if( !flag[i] ){
prime[++ncnt] = i;
f[i] = qpow( i , k );
}
for( int j = 1 ; 1ll * i * prime[j] <= k+3 ; j ++ ){
flag[i*prime[j]] = 1;
if( !f[i*prime[j]] ) f[i*prime[j]] = mul( f[i] , f[prime[j]] );
if( i % prime[j] == 0 )
break;
}
}
for( int i = 2 ; i <= k + 3 ; i ++ ) f[i] = add( f[i] + f[i-1] );
}
int main(){
char s1 = getchar();
int len = 0;
while( s1 >= '0' && s1 <= '9' ) ss[len++] = s1 , s1 = getchar();
Read( k );Read( mod );
for( int i = 0 ; i < len ; i ++ ){
int x = ss[i] - '0';
n = add( mul( n , 10 ) + x );
}
pre[0] = 1;jc = 1;
getf( );
for( int i = 1 ; i <= k + 2 ; i ++ ){
pre[i] = mul( pre[i-1] , n - i + mod );
jc = mul( jc , i );
}
nic[k+2] = qpow( jc , mod - 2 );
nic[0] = 1;
for( int i = k + 1 ; i >= 1 ; i -- )
nic[i] = mul( nic[i+1] , i + 1 );
suf[k+3] = 1;
for( int i = k + 2 ; i >= 1 ; i -- ){
suf[i] = mul( suf[i+1] , n - i + mod );
}
int ans = 0;
for( int i = 1 ; i <= k + 2 ; i ++ ){
int s = mul( nic[i-1] , nic[k+2-i] );
int tot = mul( mul( f[i] , mul( pre[i-1] , suf[i+1] ) ) , s );
if( ( k + 2 - i ) & 1 ) tot = add( mod - tot );
ans = add( ans + tot );
}
printf( "%d" , ans );
return 0;
}
拉格朗日插值求系数
既然可以算出函数值,那么是否可以支持求系数呢?其实就是把最开始的式子作为一个未知数,将其暴力展开就可以了
好的,既然已经学会了这个,就看一道例题:Shlw loves matrix II
发现直接快速幂过不了,于是要用其它方式
这里需要拓展关于A矩阵的特征多项式, f ( x ) = d e t ( A − x I ) I f(x) = det(A-xI) I f(x)=det(A−xI)I是单位矩阵
那么有定理f(A) = 0,于是用拉格朗日插值把多项式的系数存起来,考虑怎样算答案
由于f(A)= 0 所以 A k A^{k} Ak是可以用 A k − 1 A^{k-1} Ak−1到 A 0 A^{0} A0表示出来,移项即可
那么 A k + 1 A_{k+1} Ak+1也可以用 A k A^{k} Ak到 A 0 A^{0} A0表示,即也可以用 A k − 1 A^{k-1} Ak−1到 A 0 A^{0} A0表示出来
这里需要用到多项式取模的方法(暴力的但是我不会)那么举个例子,现在已经有:
f ( A ) = 2 A 4 + A 3 + A 2 + 3 A + 1 f(A) = 2A^4 + A^3 + A^2 + 3A + 1 f(A)=2A4+A3+A2+3A+1
现在要化简这个 g ( A ) = 2 A 6 + 3 A 5 + 4 A 3 + 2 A 2 + A g(A) = 2A^6 + 3A^5 + 4A^3 + 2A^2 + A g(A)=2A6+3A5+4A3+2A2+A
那么直接用 g ( A ) − = A 2 f ( A ) g(A)-=A^2f(A) g(A)−=A2f(A)就可以了,这个是可以使用快速幂的,这里就是对系数进行快速幂
最后直接把A代入即可
#include
using namespace std;
const int MAXN= 103;
const int mod = 1e9 + 7;
int n;char n1[10003];
int f[MAXN] , a[MAXN][MAXN] , s1[MAXN][MAXN];
int mul( int x , int y ){
return 1ll * x * y % mod;
}
int add( int x ){
return x >= mod ? x - mod : x;
}
int qpow( int x , int y ){
int sum = 1;
while( y ){
if( y & 1 ) sum = mul( sum , x );
x = mul( x , x );
y >>= 1;
}
return sum;
}
struct node{
int s[56][56] , n , m;
void init(){
for( int i = 1 ; i <= n ; i ++ )
for( int j = 1 ; j <= n ; j ++ ) s[i][j] = 0;
}
friend node operator * ( node a , node b ){
node c;c.n = a.n , c.m = b.m;
for( int i = 1 ; i <= c.n ; i ++ ){
for( int j = 1 ; j <= c.m ; j ++ ){c.s[i][j] = 0;
for( int k = 1 ; k <= a.m ; k ++ )
c.s[i][j] = add( c.s[i][j] + mul( a.s[i][k] , b.s[k][j] ) );
}
}
return c;
}
} ;
struct node1{
int s[103];
void init(){
memset( s , 0 , sizeof( s ) );
}
friend node1 operator + ( node1 a , node1 b ){
node1 c;c.init();
for( int i = 0 ; i <= ( n << 1 ) ; i ++ )
c.s[i] = add( a.s[i] + b.s[i] );
return c;
}
friend node1 operator * ( node1 a , int b ){
node1 c;c.init();
for( int i = 0 ; i <= (n << 1) ; i ++ )
c.s[i] = mul( a.s[i] , b );
return c;
}
friend node1 operator * ( node1 a , node1 b ){
node1 c;c.init();
for( int i = 0 ; i <= n ; i ++ ){
for( int j = 0 ; j <= n ; j ++ )
c.s[i+j] = add( c.s[i+j] + mul( a.s[i] , b.s[j] ) );
}
return c;
}
friend node1 operator % ( node1 a, node1 b ){
for( int i = n ; i >= 0 ; i -- ){
int tmp = add( mod - mul( a.s[i+n] , qpow( b.s[n] , mod - 2 ) ) );
for( int j = 0 ; j <= n ; j ++ )
a.s[i+j] = add( a.s[i+j] + mul( tmp , b.s[j] ) );
}
return a;
}
};
int det( ){
int flag = 1;
for( int i = 1 ; i <= n ; i ++ ){
int k = i;
if( !a[k][i] ){
while( k <= n && !a[k][i] ) k ++;
}
if( k != i ){
flag *= -1;
for( int j = 1 ; j <= n ; j ++ ) swap( a[i][j] , a[k][j] );
}
int p = qpow( a[i][i] , mod - 2 );
for( int j = i + 1 ; j <= n ; j ++ ){
if( !a[j][i] ) continue;
int tmp1 = mul( a[j][i] , p );
for( int k = 1 ; k <= n ; k ++ ){
a[j][k] = add( a[j][k] - mul( a[i][k] , tmp1 ) + mod );
}
}
}
int sum = 1;
for( int i = 1 ; i <= n ; i ++ ) sum = mul( sum , a[i][i] );
if( flag == -1 ) sum = add( mod - sum );
return sum;
}
node1 cf( node1 a , int y ){
node1 c;c.init();
c.s[0] = mul( a.s[0] , y );
for( int i = 1 ; i <= n << 1 ; i ++ )
c.s[i] = add( a.s[i-1] + mul( a.s[i] , y ) );
return c;
}
int main(){
scanf( "%s" , n1 );scanf( "%d" , &n );
for( int i = 1 ; i <= n ; i ++ )
for( int j = 1 ; j <= n ; j ++ )
scanf( "%d" , &s1[i][j] );
for( int i = 1 ; i <= n + 1 ; i ++ ){
memcpy( a , s1 , sizeof( s1 ));
for( int j = 1 ; j <= n ; j ++ ) a[j][j] = add( a[j][j] + mod - i );
f[i] = det();
//printf( "%d\n" , f[i] );
}
node1 co;co.init();
for( int i = 1 ; i <= n + 1; i ++ ){
node1 tot;tot.init();
tot.s[0] = 1;
for( int j = 1 ; j <= n + 1; j ++ ){
if( i != j ){
tot = cf( tot , mod - j );
tot= tot * qpow( add( i - j + mod ) , mod - 2 );
}
}
tot = tot * f[i];
co = co + tot;
}
node1 qp , q;qp.init();q.init();
qp.s[0] = 1;q.s[1] = 1;
int len = strlen( n1 );
for( int i = len - 1 ; i >= 0 ; i -- ){
if( n1[i] == '1' ){
qp = qp * q % co;
}
q = q * q % co;
}
node ans , k , kk;ans.init();k.init();
for( int i = 1 ; i <= n ; i ++ )
for( int j = 1 ; j <= n ; j ++ ) kk.s[i][j] = s1[i][j];
kk.n = kk.m = k.n = k.m = n;
for( int i = 1 ; i <= n ; i ++ ) k.s[i][i] = 1;
for( int i = 0 ; i <= n ; i ++ ){
for( int j = 1 ; j <= n ; j ++ )
for( int k1 = 1 ; k1 <= n ; k1 ++ )
ans.s[j][k1] = add( ans.s[j][k1] + mul( k.s[j][k1] , qp.s[i] ) );
k = k * kk;
}
for( int i = 1 ; i <= n ; i ++ ){
for( int j = 1 ; j <= n ; j ++ ) printf( "%d " , ans.s[i][j] );
printf( "\n" );
}
return 0;
}
例题
虽然前面已经有了一些题,但是还不够
例题1 教科书般的亵渎
这道题最好的是翻译,是在是太好du懂liu了
其实化简后就变成了一个自然数幂之和
那么直接上即可
#include
using namespace std;
#define ll long long
const int MAXN = 65;
const int mod = 1e9 + 7;
ll pre[MAXN] , jc[MAXN] , suf[MAXN] , f[MAXN] , a[MAXN];
int k;
ll mul( ll x , ll y ){
return 1ll * x * y % mod;
}
ll add( ll x ){
return x >= mod ? x - mod : x;
}
ll qpow( ll x , ll y ){
ll sum = 1;
while( y ){
if( y & 1 ) sum = mul( sum , x );
x = mul( x , x );
y >>= 1;
}
return sum;
}
ll solve( ll n ){
ll ans = 0;
pre[0] = 1;jc[0] = 1;
for( int i = 1 ; i <= k + 2 ; i ++ ){
int t = qpow( i , k );
f[i] = add( f[i-1] + t );
pre[i] = mul( pre[i-1] , n - i + mod );
jc[i] = mul( jc[i-1] , i );
}
suf[k+3] = 1;
for( int i = k + 2 ; i >= 1 ; i -- ){
suf[i] = mul( suf[i+1] , n - i + mod );
}
for( int i = 1 ; i <= k + 2 ; i ++ ){
ll s = mul( jc[i-1] , jc[k+2-i] );
ll tot = mul( mul( f[i] , mul( pre[i-1] , suf[i+1] ) ) , qpow( s , mod - 2 ) );
if( ( k + 2 - i ) & 1 ) tot = add( mod - tot );
ans = add( ans + tot );
}
return ans;
}
ll n;
int main(){
int t;scanf( "%d" , &t );
while( t -- ){
memset( suf , 0 , sizeof( suf ) );
memset( jc , 0 , sizeof( jc ) );
memset( pre , 0 , sizeof( pre ) );
memset( f , 0 , sizeof( f ) );
scanf( "%lld%d" , &n , &k );
k ++;
for( int i = 1 ; i < k ; i ++ ) scanf( "%lld" , &a[i] );
sort( a + 1 , a + k );
ll ans1 = 0;
for( int i = 0 ; i < k ; i ++ ){
ll sum = solve( n - a[i] );
for( int j = i + 1 ; j < k ; j ++ ){
sum = add( sum - qpow( a[j] - a[i] , k ) + mod );
}
ans1 = add( sum + ans1 );
}
printf( "%lld\n" , ans1 );
}
return 0;
}
例题2 calc BZOJ 2655
这道题的意义在于它是一道dp+拉格朗日插值优化的
令 d p [ i ] [ j ] dp[i][j] dp[i][j]表示已经选了i个点,在1-j中选的数,现在选的序列是递增的总贡献,转移为:
d p [ i ] [ j ] = d p [ i ] [ j − 1 ] + d p [ i − 1 ] [ j − 1 ] ∗ j dp[i][j] = dp[i][j-1] + dp[i-1][j-1] * j dp[i][j]=dp[i][j−1]+dp[i−1][j−1]∗j
最后再乘上阶乘即可
但是发现j这一维是巨大的,一般这种东西就是矩阵乘法,但是今天可以有拉格朗日来解决
首先要证明这个dp是一个多项式形式的,为什么呢?我们用自然数幂和证明的方式想一下,首先将 d p [ n ] [ A ] − d p [ n ] [ A − 1 ] dp[n][A] - dp[n][A-1] dp[n][A]−dp[n][A−1],发现最后答案是 d p [ i − 1 ] [ j − 1 ] ∗ j dp[i-1][j-1]*j dp[i−1][j−1]∗j,也就是跟n这一维的指数不见了,那么大胆猜测,如果令 g ( n ) g(n) g(n)表示n这一维的指数,那么就有 g ( n ) − 1 = g ( n − 1 ) + 1 , g ( n ) = g ( n − 1 ) + 2 g(n)-1=g(n-1)+1 ,g(n) = g(n-1)+2 g(n)−1=g(n−1)+1,g(n)=g(n−1)+2因此它的指数是公差为2的等差数列,那么最后算2n+1个就可以求出多项式
#include
using namespace std;
const int MAXN = 1003;
int g[MAXN] , jc , f[MAXN][MAXN] , n , A , mod;
int mul( int x , int y ){
return 1ll * x * y % mod;
}
int add( int x ){
return x >= mod ? x - mod : x;
}
int qpow( int x , int y ){
int sum = 1;
while( y ){
if( y & 1 ) sum = mul( sum , x );
x = mul( x , x );
y >>= 1;
}
return sum;
}
int main(){
scanf( "%d%d%d" , &A , &n , &mod );
jc = 1;
for( int i = 0 ; i <= n * 2 + 1; i ++ )f[i][0] = 1;
for( int i = 1 ; i <= n * 2 + 1; i ++ ){
for( int j = 1 ; j <= min( n , i ) ; j ++ ){
f[i][j] = add( mul( f[i-1][j-1] , i ) + f[i-1][j] );
}
g[i] = i;
}
for( int i = 1 ; i <= n ; i ++ ){
jc = mul( jc , i );
}
int ans = 0;
for( int i = 1 ; i <= n * 2 + 1; i ++ ){
int sum1 = f[i][n] , sum2 = 1;
for( int j = 1 ; j <= n * 2 + 1; j ++ ){
if( i != j ){
sum1 = mul( sum1 , add( A - g[j] + mod ) );
sum2 = mul( sum2 , add( g[i] - g[j] + mod ) );
}
}
ans = add( ans + mul( sum1 , qpow( sum2 , mod - 2 ) ) ) ;
}
printf( "%d" , mul( jc , ans ) );
return 0;
}
例题3 成绩比较
这确实是一道好题,同时这道题是纯数学,在考场上还是很难想到用拉格朗日插值做的
突破口在于容斥,通过二项式反演不会证乱搞得到:
a n s = ∑ i = k n ( − 1 ) i − k ( i k ) ( n i ) ∏ j = 1 m ( n − 1 − i n − i − r [ j ] ) ∑ k = 1 k < = u [ j ] ( u [ j ] − k ) r [ j ] − 1 k n − r [ j ] ans = \sum_{i=k}^{n} (-1)^{i-k}\tbinom{i}{k} \tbinom{n}{i} \prod_{j=1}^{m} \tbinom{n-1-i}{n-i-r[j]}\sum_{k=1}^{k<=u[j]}(u[j]-k)^{r[j]-1}k^{n-r[j]} ans=∑i=kn(−1)i−k(ki)(in)∏j=1m(n−i−r[j]n−1−i)∑k=1k<=u[j](u[j]−k)r[j]−1kn−r[j]
可以解释一下,其实可以分成两部分看,第一部分是 ∑ i = k n ( − 1 ) i − k ( i k ) \sum_{i=k}^{n} (-1)^{i-k\tbinom{i}{k}} ∑i=kn(−1)i−k(ki)是容斥的操作,而后面计算的是指现在至少有i个人被B神碾压的方案数,首先每一科都要考虑,然后计算没有被碾压但是这一科的成绩比B差的人的情况
然后再枚举B这一科得了多少分,那么比他低的人的分数就要k种,否则就有r[j]-k种
正确性显然
但是这样的时间复杂度达不到期望,发现最后有一个 k n − r [ j ] k^{n-r[j]} kn−r[j]且u[j]很大,那么考虑使用拉格朗日插值优化。其实时间复杂度大主要是因为枚举k,那么就对k优化
∑ k = 1 k < = u [ j ] ( u [ j ] − k ) r [ j ] − 1 k n − r [ j ] \sum_{k=1}^{k<=u[j]}(u[j]-k)^{r[j]-1}k^{n-r[j]} ∑k=1k<=u[j](u[j]−k)r[j]−1kn−r[j]
看到幂次较大,不难想到用二项式定理:
∑ k = 1 k < = u [ j ] k n − r [ j ] ∑ l = 0 l < r [ j ] ( r [ j ] − 1 l ) u [ j ] r [ j ] − 1 − l ( − k ) l \sum_{k=1}^{k<=u[j]}k^{n-r[j]}\sum_{l=0}^{l
把外面的k带到里面去,再把-1提出来,这样sigma就可以交换了:
∑ l = 0 l < r [ j ] ( − 1 ) l ( r [ j ] − 1 l ) u [ j ] r [ j ] − 1 − l ∑ k = 1 k < = u [ j ] k n − r [ j ] − l \sum_{l=0}^{l
最后发现k就是一个自然数幂求和,做完了
using namespace std;
#define ll int
const int MAXN = 203;
const int mod = 1e9 + 7;
int jc[MAXN] , nic[MAXN] , ni[MAXN] , R[MAXN] , n , m ,K , U[MAXN] , lage[MAXN][MAXN] , pre[MAXN] , suf[MAXN] , f[MAXN];
int mul( int x , int y ){
return 1ll * x * y % mod;
}
int add( int x ){
return x >= mod ? x - mod : x;
}
int qpow( int x , int y ){
int sum = 1;
while( y ){
if( y & 1 ) sum = mul( sum , x );
x = mul( x , x );
y >>= 1;
}
return sum;
}
int C( int x , int y ){
return mul( jc[x] , mul( nic[y] , nic[x - y ] ) );
}
ll solve( ll n , ll k ){
ll ans = 0;
pre[0] = 1;
for( int i = 1 ; i <= k + 1; i ++ ){
ll t = qpow( i , k - 1 );
f[i] = add( f[i-1] + t );
pre[i] = mul( pre[i-1] , n - i + mod );
}
suf[k+2] = 1;
for( int i = k + 1; i >= 1 ; i -- ){
suf[i] = mul( suf[i+1] , n - i + mod );
}
for( int i = 1 ; i <= k + 1 ; i ++ ){
ll s = mul( jc[i-1] , jc[k+1-i] );
ll tot = mul( mul( f[i] , mul( pre[i-1] , suf[i+1] ) ) , qpow( s , mod - 2 ) );
if( ( k +1- i ) & 1 ) tot = add( mod - tot );
ans = add( ans + tot );
}
return ans;
}
int main(){
scanf( "%d%d%d" , &n , &m , &K );
for( int i = 1 ; i <= m ; i ++ ) scanf( "%d" , &U[i] );
for( int i = 1 ; i <= m ; i ++ ) scanf( "%d" , &R[i] );
jc[0] = jc[1] = nic[0] = nic[1] = ni[0] = ni[1] = 1;
for( int i = 2 ; i <= n ; i ++ ){
jc[i] = mul( jc[i-1] , i );
ni[i] = mul( mod - ( mod / i ) , ni[mod%i] );
nic[i] = mul( nic[i-1] , ni[i] );
}
int nn = n;
for( int i = 1 ; i <= m ; i ++ ){
for( int j = 0 ; j < R[i] ; j ++ ){
lage[i][j] = solve( U[i] , n - R[i] + j + 1 );
}
nn = min( nn , n - R[i] + 1 );
}
int ans = 0;
for( int i = K ; i < nn ; i ++ ){
int sum1 = mul( C( i , K ) , C( n - 1 , i ) );
for( int j = 1 ; j <= m ; j ++ ){
sum1 = mul( sum1 , C( n - i - 1 ,n - R[j] - i ) );
int tot = 0;
for( int k = 0 ; k <= R[j] - 1 ; k ++ ){
int p = mul( C( R[j] - 1 , k ) , mul( qpow( U[j] , R[j] - 1 - k ) , lage[j][k] ) );
if( k & 1 ) tot = add( tot - p + mod );
else tot = add( tot + p );
}
sum1 = mul( sum1 , tot );
}
if( i - K & 1 )
ans = add( ans - sum1 + mod );
else
ans = add( ans + sum1 );
}
printf( "%d" , ans );
return 0;
}