R语言建立ARIMA模型预测数据
目录
确定研究目的以及确定因变量和自变量
数据预处理
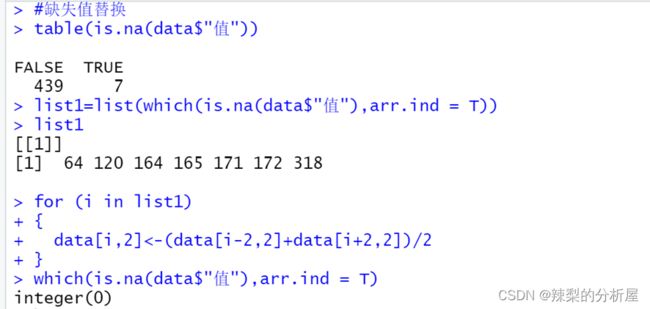
判断有无缺失值
创建时间序列
平稳性检验
季节性处理
白噪声检验
模型选取与模型评估
最终模型与预测
结论
确定研究目的以及确定因变量和自变量
研究目的:建立ARIMA模型,预测接下来的 14 天的数值。
数据预处理
判断有无缺失值
发现存在七个缺失值,用对应序列平均值填充,观察缺失值位置,发现数据出现连续缺失,故取数据前后间隔一个点,取两点的平均值填充。
创建时间序列
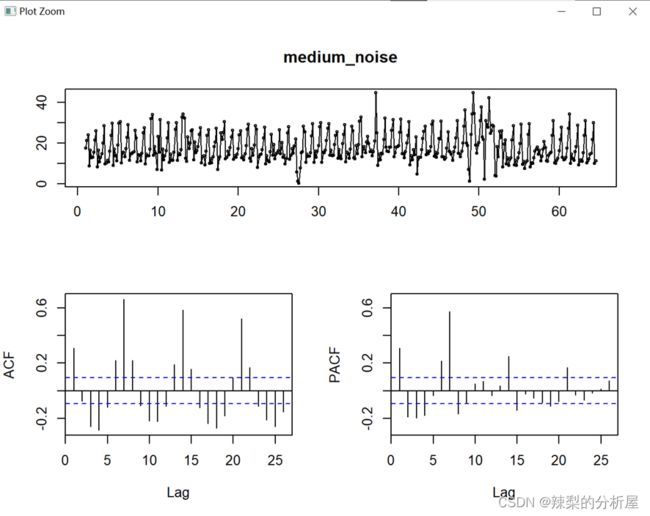
以7天为一周期,观察序列图,发现数据呈现较小的长期趋势,明显的季节性。
观察自相关图判断季节性
观察结果:观察到明显的季节性,较小的长期趋势(差分d值为0)
平稳性检验
对数据进行adf检验:
观察结果得,当 p 值小于 0.01(小于 5%的临界值)时,可以拒绝数据不平稳的零假设。所以我们有足够的证据表明数据不是平稳的。
季节性处理
由上述可得,数据存在季节性,所以对数据季节性差分。
观察结果可得:对于自相关图可得,季节项:lag为7的自相关系数超过滞后的临界区域,可确定季节项的Q为1,对于偏自相关图可得,季节性:lag为7、14和21的偏自相关系数超过滞后的临界区域,可确定季节项的P为1或2或3,非季节性,lag为1后lag为2突然下降趋近0,先确定非季节项的p为1。
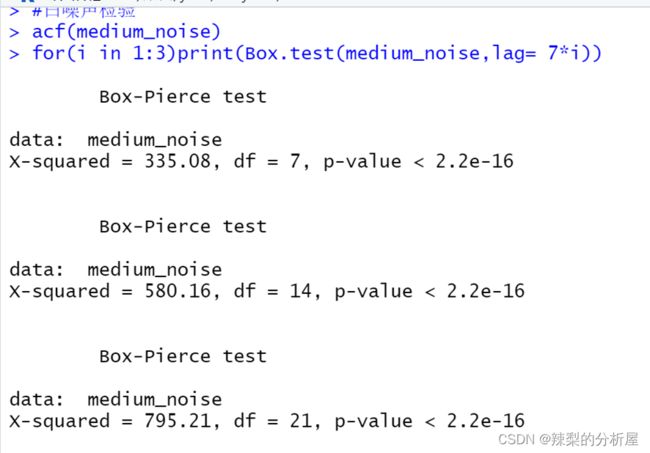
白噪声检验
对数据进行白噪声检验,延迟7期、延迟14期、21期的QLB统计量的值,并判断该序列的随机性(α=0.05):
观察结果得,当 p 值小于 0.01(小于 5%的临界值)时,可以拒绝纯随机的原假设。所以我们有足够的证据表明数据非白噪声。
模型选取与模型评估
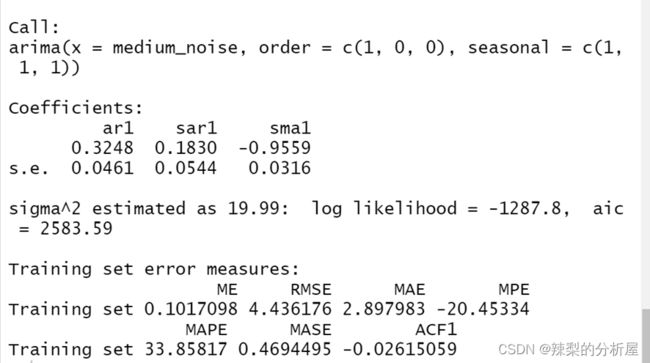
(1)、第一个模型
由上述可得非季节项(p,d,q)——(1,0,0),季节项(P,D,Q)——(1,1,1)建立模型。
观察结果:aic为2583.59,均方根误差为4.436176,模型拟合效果较好。
观察结果得:自相关和非自相关图仅有第20项超过滞后的临界区域,消除了大部分季节性。
(2)、第二个模型
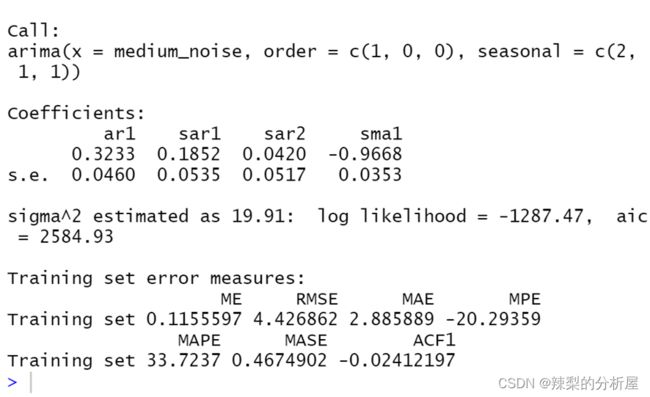
由上述可得非季节项(p,d,q)——(1,0,0),季节项(P,D,Q)——(2,1,1)建立模型。
观察结果:aic为2584.93,均方根误差为4.426862,模型拟合效果较好。
观察结果得:自相关和非自相关图仅有第20项超过滞后的临界区域,消除了大部分季节性。
(3)、第三个模型
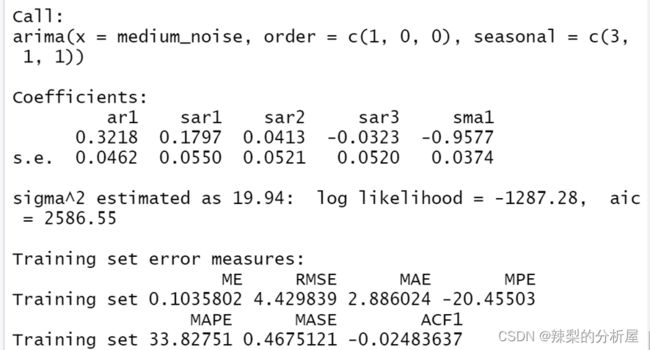
由上述可得非季节项(p,d,q)——(1,0,0),季节项(P,D,Q)——(3,1,1)建立模型。
观察结果:aic为2586.55,均方根误差为4.429839,模型拟合效果较好
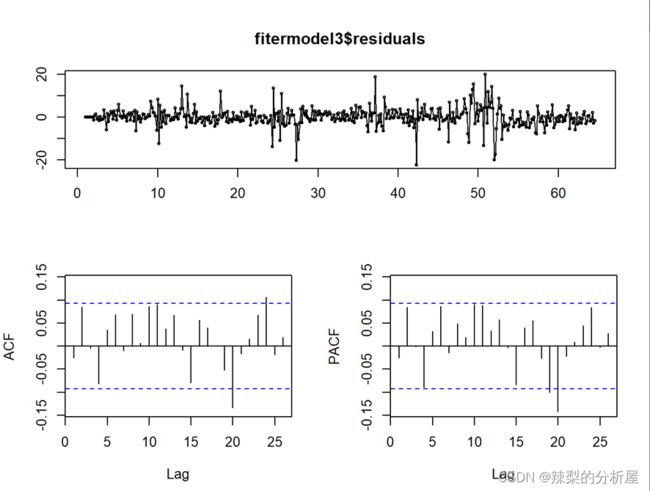
观察结果得:自相关和非自相关图仅有第20项超过滞后的临界区域,消除了大部分季节性。
最终模型与预测
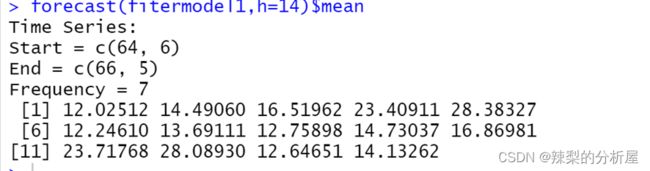
综上模型,最终选择参数为由上述可得非季节项(p,d,q)——(1,0,0),季节项(P,D,Q)——(1,1,1)ARIMA模型,R方为0.636,没有离散值,均方根误差为4.415,得出预测14天的数据。
结论
我选用了均方误差和AIC为标准,对于这次试验的数据,仅通过PACF得到第一个P值便可以使模型拟合,如果ACF图或PACF 图出现多次截尾Box-Jenkins 方法反复迭代得到最适的非季节的p和q值,得到最优模型。对于非季节性的数据我们需通过Box-Jenkins方法反复迭代寻找最适的p和q,而对于季节性的数据它是得先季节性差分(D),并且确定P和Q消除季节性,再通过Box-Jenkins方法反复迭代寻找最适的p和q,知道大部分数据在滞后的临界区域内,除部分特别数据可忽略。可以像实验中先固定P值、Q值,再迭代p、q值,如果模型效果依旧不好,变换P、Q值,再迭代p、q值。R语言自带auto.arma以最小化AICc值找到最优模型。新人博主,有什么不对的地方还望指正