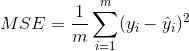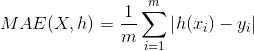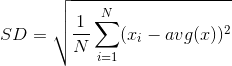Tensorflow2.0入门基础——多元线性回归(波士顿房价)以及网络搭建方法
**
Tensorflow2.0入门基础——多元线性回归(波士顿房价)以及网络搭建方法
(1)第一步首先导入数据集,这里我们选用波士顿房价预测
如果已经下载好了可以直接导入数据(也可以直接加我qq1217649965找我要),如果没有下载好,可以使用注释的部分导入
#如果没有下载好,可以使用注释的部分导入
# from sklearn.datasets import load_boston
# import matplotlib.pyplot as plt
# dataset = load_boston()import pandas as pd
import numpy as np
data = pd.read_csv('D:\\Download\\Anacond\\boston_house_prices.csv',header=0)
# header=0 取第一行为列标签 第一列作为行名字只需要在 加上 index _col = 0
data
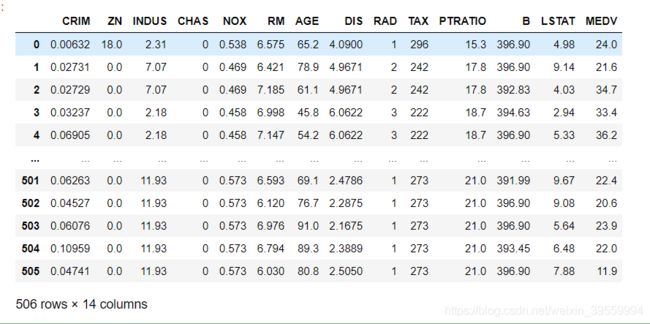
总共有13组特征值,1组目标值,总计506行数据。
数据集中的每一行数据都是对波士顿周边或城镇房价的描述:
CRIM: 城镇人均犯罪率;
ZN: 住宅用地所占比例
INDUS: 城镇中非住宅用地所占比例;
CHAS:虚拟变量,用于回归分析
NOX: 环保指数;
RM: 每栋住宅的房间数
AGE: 1940 年以前建成的自住单位的比例;
DIS: 距离 5 个波士顿的就业中心的加权距离。
RAD: 距离高速公路的便利指数
TAX: 每一万美元的不动产税率
PRTATIO: 城镇中的教师学生比例
B: 城镇中的黑人比例
LSTAT: 地区中有多少房东属于低收入人群
MEDV: 自住房屋房价中位数(是目标值)
然后导入Tensorflow2.0,查看自己的Tensorflow版本是不是2.0的版本
import tensorflow as tf
print('Tensorflow Version: {}'.format(tf.__version__))
我的版本是2.1
![]()
(2)接下来将数据划分为特征值和目标值两部分,并且进行数据的预处理,归一化
#获取特征和标签值,总共有13组标签和1组特征
x_data = data.iloc[:,:-1] #获取前13组特征
y_data = data.iloc[:,-1] #获取标签
"""数据归一化(最大最小方法)"""
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(x_data) #训练
x_data = scaler.transform(x_data) #此时输出的x_data就是数组了
"""数据归一化(标准化方法)"""
# from sklearn.preprocessing import StandardScaler
# scaler = StandardScaler()
# scaler.fit(x_data)
# x_data = scaler.transform(x_data)
y_data = np.array(y_data) #将y_data转换成数组
此处归一化是使用的最大最小化方法,归一化用的比较多的就是以下两种,如果不懂得可以参考这位博主讲解的原理
https://blog.csdn.net/qq_24831889/article/details/83344638?depth_1-utm_source(使用sklearn预处理数据之标准化、归一化、正则化)
(2)最小最大化
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler() #创建对象
scaler.fit(data)
data = scaler.transform(data)
(4)标准化
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(data)
data = scaler.transform(data)
(3)接下来打了tensorflow2.0的核心了,构建模型,tensorflow2.0比1.X简便太多了,非常容易学,下面这位大佬详细总结了2.0与1.X之间的对比
https://blog.csdn.net/weixin_43038300/article/details/94971193#Tensorflow1x__Tensorflow20_20(深度学习基础2: tensorflow 2.0 VS 1.x)
https://blog.csdn.net/javastart/article/details/102525102(升级到tensorflow2.0,我整个人都不好了)
"""顺序模型:类似于搭积木一样一层、一层放上去"""
model = tf.keras.Sequential()
"""添加层:其实就是 wx+b"""
model.add(tf.keras.layers.Dense(1,input_shape = (13,))) #输出是1维数据,输入是13维数据
"""查看网络结构"""
model.summary()

仅仅只有一层,是最简单的线性回归模型tf.keras.layers.Dense相当于执行了wx+b的操作,所以有13个权重w和一个偏置b,总共14个参数,没有隐含层
model = tf.keras.Sequential()相当于一个容器,里面可以一层一层储存东西
tf.keras.layers.Dense(1,input_shape = (13,)),只有一层神经单元,所以此层就是输出层,1就相当于是输出神经元个数就是1个,如果是分类问题,有几类就代表输出神经元的个数是几,后面的input_shape = (13,),就是指输入的是一维的数组,但是一维数组里面有13个元素。
注意啦(k,)代表的是一维数组里面有k个数值,并不是代表13维,但是输入有几个是未知的,我们只是知道输入的size是一维里面13个元素,但到底有几个输入是没有规定的
此处我们可以尝试着自己添加一个隐含层,有两种方法:
方法一:model.add()方法,执行一次添加一层(我这里没加激活函数,后面讲的时候再加)
“”“顺序模型:类似于搭积木一样一层、一层放上去”""
model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(16,input_shape = (13,))) ,
model.add(tf.keras.layers.Dense(8)),
model.add(tf.keras.layers.Dense(1)),
大家有没有发现只有第一层填写了input_shape = (13,))输入数据的形状,后面的数据都没有填写,因为后面的层都会自己推算出来,不用人为的填写,只需要填写自己本层神经元数量即可。
**方法二:直接把所有的层塞到篮子里面model = tf.keras.Sequential()
一层一层叠加,注意要用数组的形式塞入[, , , , , ]
model = tf.keras.Sequential([
tf.keras.layers.Dense(64, activation=‘relu’, input_shape=(13,)),
tf.keras.layers.Dense(64, activation=‘relu’),
tf.keras.layers.Dense(1)
])
(3)接下来就进入模型配置和编译的阶段
"""编译,配置"""
model.compile(optimizer = 'adam',
loss = 'mse',
metrics=['mae','mse']
)
"""训练数据"""
history = model.fit(x_data, y_data, epochs = 1000)
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist['epoch'] = hist['epoch'] + 1
import matplotlib.pyplot as plt
%matplotlib notebook
# """修改列名"""
# hist.rename(columns={'mean_absolute_error':'MAE', 'mean_squared_error':'MSE'},inplace = True)
# print(hist)
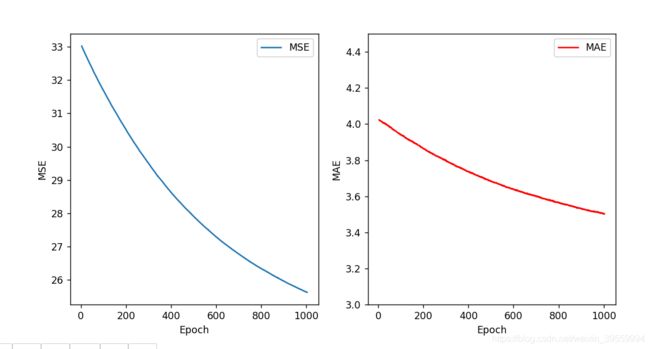
def plot_history(hist):
plt.figure(figsize=(10,5))
plt.subplot(1, 2, 1)
plt.xlabel('Epoch')
plt.ylabel('MSE')
plt.plot(hist['epoch'], hist['mse'],
label='MSE')
plt.legend()
plt.subplot(1, 2, 2)
plt.xlabel('Epoch')
plt.ylabel('MAE')
plt.plot(hist['epoch'], hist['mae'],
label = 'MAE',color ='red')
plt.ylim([3,4.5])
plt.legend()
plot_history(hist)
"""查看训练效果,从中随机提取20个数据下标"""
indices = np.random.choice(len(data), size=100)
# house_data.loc[indices,:]
count = 0
for n in indices:
count += 1
x_test = x_data[n]
x_test = x_test.reshape(1,13)
predict = model.predict(x_test)
print("——第%d个数据——"% count)
print("预测值:%f" % predict)
target = y_data[n]
print("标签值:%f" % target)
print('\n')
optimizer优化器介绍
机器学习中,有很多优化方法来试图寻找模型的最优解。比如神经网络中可以采取最基本的梯度下降法。详细原理内容请参考(机器学习:各种优化器Optimizer的总结与比较)
https://blog.csdn.net/weixin_40170902/article/details/80092628?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1
https://blog.csdn.net/limiyudianzi/article/details/84960074
共有11个优化器,以及1个tf.train.Optimizer的基类。这11个优化器分别是:
Tf.train.AdadeltaOptimizer
Tf.train.AdagradDAOptimizer
Tf.train.AdagradOptimizer
Tf.train.AdamOptimizer
Tf.train.FtrlOptimizer
Tf.train.GradientDescentOptimizer
Tf.train.MomentumOptimizer
Tf.train.ProximalAdagradOptimizer
Tf.train.ProximalGradientDescentOptimizer
Tf.train.RMSPropOptimizer
Tf.train.SyncReplicasOptimize
我们使用的是optimizer = ‘adam’,Adam优化器算是比较常用的优化器
2014年12月,Kingma和Lei Ba两位学者提出了Adam优化器,结合AdaGrad和RMSProp两种优化算法的优点。对梯度的一阶矩估计(First Moment Estimation,即梯度的均值)和二阶矩估计(Second Moment Estimation,即梯度的未中心化的方差)进行综合考虑,计算出更新步长。
主要包含以下几个显著的优点:
- 实现简单,计算高效,对内存需求少
- 参数的更新不受梯度的伸缩变换影响
- 超参数具有很好的解释性,且通常无需调整或仅需很少的微调
- 更新的步长能够被限制在大致的范围内(初始学习率)
- 能自然地实现步长退火过程(自动调整学习率)
- 很适合应用于大规模的数据及参数的场景
- 适用于不稳定目标函数
- 适用于梯度稀疏或梯度存在很大噪声的问题
综合Adam在很多情况下算作默认工作性能比较优秀的优化器
详情链接:https://www.jianshu.com/p/aebcaf8af76e
损失函数loss
以下内容参考自
https://blog.csdn.net/FrankieHello/article/details/82024526
RMSE(Root Mean Square Error)均方根误差
衡量观测值与真实值之间的偏差。
MSE(Mean Square Error)均方误差
MSE是真实值与预测值的差值的平方然后求和平均。
MAE(Mean Absolute Error)平均绝对误差
是绝对误差的平均值。
SD(Standard Deviation)标准差
方差的算术平均根。
模型评估指标
例如决定系数R2、准确度等,下面对常用的分类模型与回归模型的评估指标做一个区分归纳,
详情请看链接
https://www.cnblogs.com/dwithy/p/11577568.html