神经网络各个部分的作用 & 彻底理解神经网络
这些题目来自知识星球【CV技术指南(免费版)】的日常作业
欢迎关注公众号CV技术指南,专注于计算机视觉的技术总结、最新技术跟踪、经典论文解读、CV招聘信息。
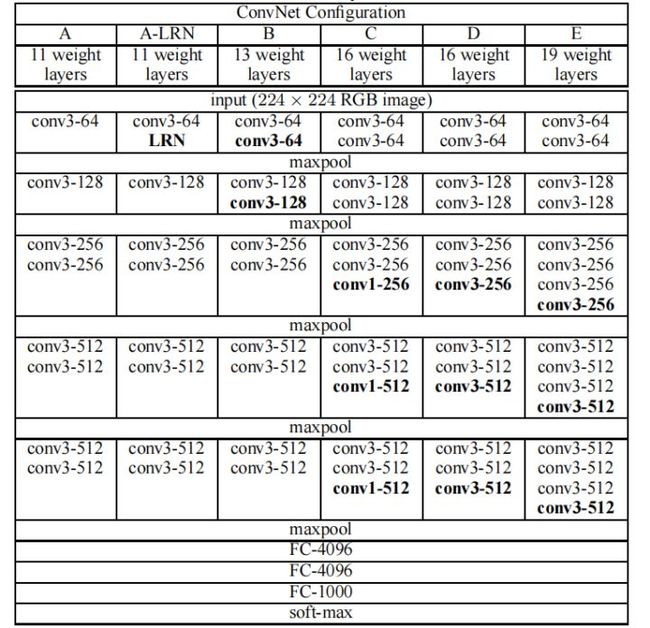
1. 神经网络的层数是如何数的?
我们说的网络越深,模型效果越好,指的是可训练参数越多,模型的特征提取能力或表示能力更好。
因此,神经网络的层数只与可训练参数的层数有关,层数等于卷积层+全连接层数量。BN层、池化层、Flatten层都不算在内。
例如下方的VGG-16。层数为:2+2+3+3+3(卷积层) + 3(全连接)。中间5层最大池化都是不算的。
2. 卷积操作的作用是什么?(为什么卷积层堆叠可以提取特征)
从单个卷积来说,它的作用是很明显的,卷积核参数是具有特定含义的矩阵,输入图像与该矩阵进行逐元素相乘,可以产生该矩阵所对应输出。
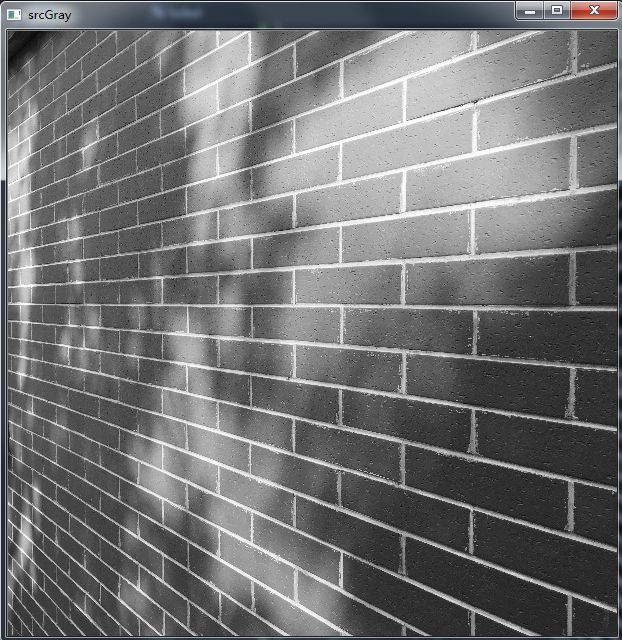
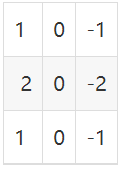
我最常举的例子就是sobel算子,对于一个如下的3x3的矩阵,其与输入图像的像素值进行逐元素相乘,可得到该图像在竖直方向上的一阶梯度,该梯度对于边缘区域有较大的值,而非边缘区域则为零。因此通过下面3x3卷积可以提取图像竖直方向的边缘特征。
当3x3卷积中的参数变成其它的情况时,可以提取别的情况的特征。当很多个卷积组合时,可以提取很多种特征。当很多卷积层堆叠时,卷积区域的感受野越来越大,可以提取更大范围的一些特征。
将其放到神经网络上来说,举个例子,给定一个映射函数y = sign(x),当x 为正时,y=1,当x为负时,y=-1。在这个映射函数下,所有的正数都为同一个类,所有的负数为另一个类。y = sign(x) 这个函数也可以理解为特征提取器,它提取了所有待测 x 的特征,这里的特征是待测x的正负号,然后同一个类的具有相同特征得到同一个输出,不同类得到不同的输出。
训练过后的神经网络就是这个映射函数,也是特征提取器,当卷积核的参数固定时,不同类的两张图片,可以被这个由很多卷积堆叠组成的特征提取器提取图像的特征,然后得到不同的输出。结合上面的sobel的例子,任何图片经过sobel竖直方向的算子,都会被提取竖直方向的边缘特征,输出竖直方向的边缘特征图。
因此,卷积由于参数的之间的特性,可以实现不同的图片经过这个卷积时,提取同样的特征,不同的图片输出不同的特征图,当很多卷积组合在一起时,可以提取图像的很多种特征,当卷积堆叠起来时,可以提取更大范围的特征和更深层次的特征。
3. 池化层的作用是什么?(为什么需要池化层)
池化层的操作是将一个窗口内的像素按照平均值加权或选择最大值来作为输出,一个窗口内仅有一个输出数据。因此,当经过池化层后,图像的尺寸会变小,计算量也会变小,相比于在池化前使用卷积,池化后同样的卷积大小具有更大的感受野。
但仅仅从缩小图像尺寸,减少计算量,获取更大感受野这个作用来说,也可以使用步长大于1的卷积来替代池化层。这在少部分模型中就有所应用。
但实际上池化层还有别的作用。
当使用最大池化时,一个窗口中仅有最大的像素值才会进入下一层,而其它位置的像素就被暂时抛弃了。之所以说暂时抛弃了,是因为在训练过程中是不断更新的,可能在下一次前传时,由于卷积核权重更新,最大的像素值就在另一个位置取到了。
那这种取最大的像素值的好处在哪呢。
结合前面我们提到的卷积核提取特征的理解,当一张图片经过sobel竖直方向的算子时,仅在竖直边缘区域输出较大的值,而其它平整区域都为零或接近为零了。如果此时经过一个最大池化层,就会发现平整区域的像素被丢下了,仅留下了竖直边缘区域的像素。接下来就仅剩下竖直边缘区域的特征继续卷积提取进一步的特征了。如果是还有其它类型的卷积核,则经过卷积+池化后,仅留下了那个类型卷积核提取的特征。
因此最大池化除了前面那两个作用,还有一个去除冗余信息、去除噪声的作用。
说到这里,理解池化的使用也很简单了,在神经网络的Backbone部分使用最大池化,用于去除噪声,去除干扰因素,在全连接层前,使用平均池化,避免丢失信息。
再给大家扩展一个知识点,如果要可视化一个训练过的卷积核,应该怎么可视化?
根据这里的理论,每张图片经过同一个卷积核时,会提取同一个类型的特征,而不符合这个特征的,输出的像素值就为零或很小了。那我们只需要随机初始化一张图片,所有像素值随机,在经过这个待可视化的卷积核时,输出的值越大,则说明越符合这个卷积核的所提取的特征,然后我们就可以利用梯度上升法,来调整像素值,不更新卷积核参数,以使得该图片在经过待可视化卷积核后输出的像素值更大。当模型收敛后,此时的图片显示的就是该卷积核所认可的特征,从而达到了可视化卷积核的目的。
池化另外还有几个特性,比较好理解,这里也列举一下,
具有平移不变性、旋转不变性。
防止过拟合。
4. 归一化层的作用是什么?(为什么需要归一化层)
第一种解释
假设输入数据包含多个特征x1,x2,…xn。每个功能可能具有不同的值范围。例如,特征x1的值可能在1到5之间,而特征x2的值可能在1000到99999之间。
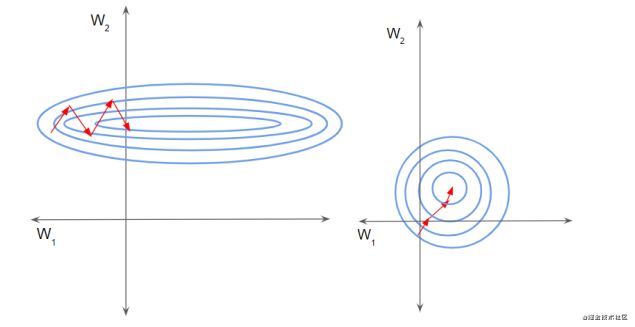
如下左图所示,由于两个数据不在同一范围,但它们是使用相同的学习率,导致梯度下降轨迹沿一维来回振荡,从而需要更多的步骤才能达到最小值。且此时学习率不容易设置,学习率过大则对于范围小的数据来说来回震荡,学习率过小则对范围大的数据来说基本没什么变化。
如下右图所示,当进行归一化后,特征都在同一个大小范围,则loss landscape像一个碗,学习率更容易设置,且梯度下降比较平稳
第二种解释(来自BN论文)
训练深度神经网络非常复杂,因为在训练过程中,随着先前各层的参数发生变化,各层输入的分布也会发生变化,图层输入分布的变化带来了一个问题,因为图层需要不断适应新的分布,因此训练变得复杂,随着网络变得更深,网络参数的细微变化也会放大。
由于要求较低的学习率和仔细的参数初始化,这减慢了训练速度,并且众所周知,训练具有饱和非线性的模型非常困难。我们将此现象称为内部协变量偏移,并通过归一化层输入来解决该问题。
4. 激活函数层的作用是什么?(为什么需要激活函数层)
数字图像是一堆0-255的数值组合而成,很神奇的是,就是这么一堆数字就形成了各种各样的图像,例如一张人脸,一个篮球,一只猫。但这仅仅是我们人肉眼看到的图像,而神经网络则是面对这些数字,并要从这对数字中得到它的类别,因此关于神经网络有另一种理论,数字图像中的图像像素值其实是在像素空间,神经网络是将图像从像素空间映射到特征空间,再从特征空间对数据进行分类。
这种映射需要通过非线性函数来实现,想想如果是线性函数,会发现仍然是在像素空间,而不管堆叠多少层的线性函数,都等同于只有一个线性函数。因此需要通过非线性函数来实现这个映射。
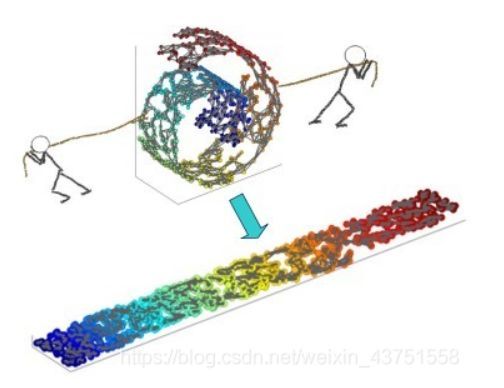
接下来从机器学习的角度来解释这个理论,对于二维坐标中的数据很好理解,数据之间的距离就是两个坐标差值的平方。对于高维中的数据就不能这么计算了。例如一个球,如果要从球的表面从一个点走到另一个点,不能通过3维的欧式距离来计算,可以通过极坐标来表示成一个二维的空间。
流形学习的观点:认为我们所能观察到的数据实际上是由一个低维流行映射到高维空间的。由于数据内部特征的限制,一些高维中的数据会产生维度上的冗余,实际上这些数据只要比较低的维度就能唯一的表示。所以直观上来讲,一个流形好比是一个d维的空间,在一个m维的空间中(m>d)被扭曲之后的结果。需要注意的是流形并不是一个形状,而是一个空间。举个例子来说,比如说一块布,可以把它看成一个二维的平面,这是一个二维的空间,现在我们把它扭一扭(三维空间),它就变成了一个流形,当然不扭的时候,它也是一个流形,欧式空间是流形的一种特殊情况。如下图所示
此处流形学习的部分参考链接:https://blog.csdn.net/weixin_43751558/article/details/112910899
根据图像像素值是在像素空间的这个理论,数字图像也是这样的高维空间,需要将它映射到另一个空间,才能将它进行分类。
5. 损失函数的作用是什么?
损失函数用来表现预测数据与实际数据的差距程度。
6. 全连接层的作用是什么?
根据前面两种理论,全连接层的作用都是对数据进行分类。第一种是图像通过卷积层提取了很多特征,第二种是将图像从像素空间映射到了特征空间,在特征空间可以像在二维平面上对两类数据进行分类那样,全连接层就是相当于一个超平面,将各个类别在特征空间将它们分开。
星球内每天都会布置一些作业,这些作业会引导大家去学一些东西。如果有人觉得自己一个学习没有动力,或想要养成一个很好的学习习惯,每天完成在知识星球内的作业是一个不错的做法。
另外,我们建立了一个交流群,群内会经常发布最近几天出来的最新顶会论文,大家可以下载这些论文去阅读,如果看完写一个解读,可以给我们投稿,我们将付稿费。既可以保持阅读最新顶会、持续输出的习惯,又能提高写作能力,日后还可以在简历上写在公众号CV技术指南上投稿几十、一百余篇文章,对于提高能力、保持学习态度、个人履历等方面会是一大作用。
欢迎关注公众号CV技术指南,专注于计算机视觉的技术总结、最新技术跟踪、经典论文解读、CV招聘信息。
关注公众号添加编辑的微信号可邀请加入技术群和免费版知识星球。
其它文章
招聘 | 迁移科技招聘深度学习、视觉、3D视觉、机器人算法工程师等多个职位
计算机视觉入门路线
YOLO系列梳理(一)YOLOv1-YOLOv3
YOLO系列梳理(二)YOLOv4
YOLO系列梳理(三)YOLOv5
Attention Mechanism in Computer Vision
从零搭建Pytorch模型教程(五)编写训练过程--一些基本的配置
从零搭建Pytorch模型教程(四)编写训练过程--参数解析
从零搭建Pytorch模型教程(三)搭建Transformer网络
从零搭建Pytorch模型教程(二)搭建网络
从零搭建Pytorch模型教程(一)数据读取
StyleGAN大汇总 | 全面了解SOTA方法、架构新进展
一份热力图可视化代码使用教程
一份可视化特征图的代码
工业图像异常检测研究总结(2019-2020)
关于快速学习一项新技术或新领域的一些个人思维习惯与思想总结