数据挖掘实战—财政收入影响因素分析及预测
文章目录
-
- 引言
- 一、数据探索
-
- 1.数据质量分析
-
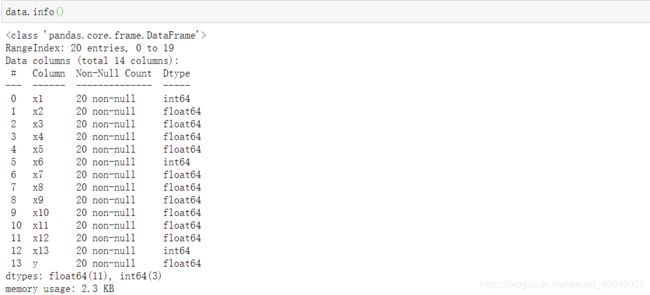
- 1.1 缺失值分析
- 1.2 异常点分析—箱型图分析
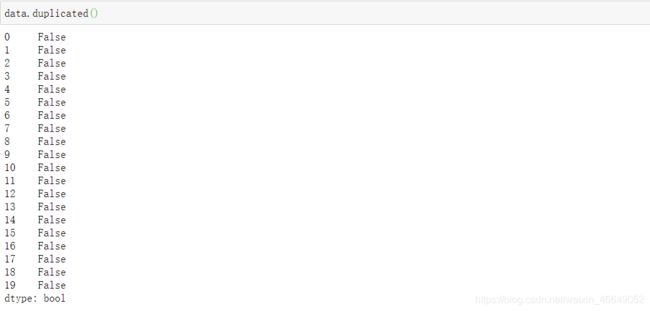
- 1.3 重复数据分析
- 2.数据特征分析
-
- 2.1 描述性统计分析
- 2.2 分布分析
- 2.3 相关性分析
- 二、数据预处理
- 三、模型构建
-
- 1.灰色预测模型
- 2.构建支持向量机回归模型
传送门:
- 数据挖掘实战—财政收入影响因素分析及预测
- 数据挖掘实战—航空公司客户价值分析
- 数据挖掘实战—商品零售购物篮分析
- 数据挖掘实战—基于水色图像的水质评价
- 数据挖掘实战—家用热水器用户行为分析与事件识别
- 数据挖掘实战—电商产品评论数据情感分析
引言
本文运用数据挖掘技术对市财政收入进行分析,挖掘其中的隐藏的运行模式,并对未来两年的财政收入进行预测,希望能够帮助政府合理地控制财政收支,优化财政建设,为制定相关决策提供依据。定义数据挖掘目标如下:
- 分析、识别影响地方财政收入的关键属性
- 预测2014年和2015年的财政收入
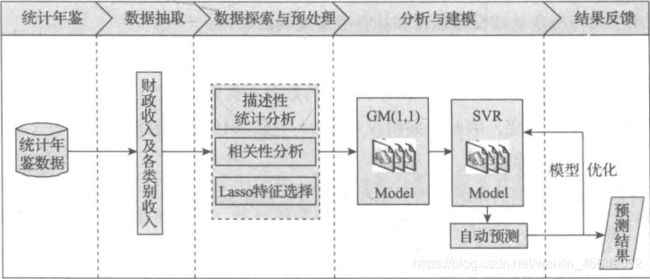
本文数据挖掘主要包括以下步骤:
- 对原始数据进行探索性分析,了解原始属性之间的相关性
- 利用Lasso特征选择模型提取关键属性
- 建立单个属性的灰色预测模型以及支持向量模回归预测模型
- 使用支持向量回归预测模型得出2014年至2015年财政收入的预测值
- 模型评价
一、数据探索
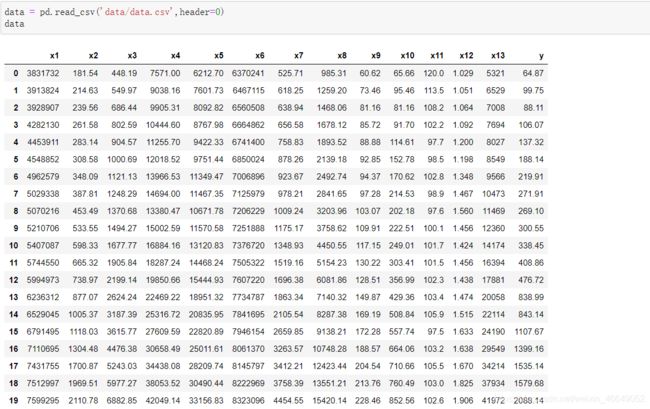
data.csv数据,提取码:1234
表中各属性名称及属性说明:

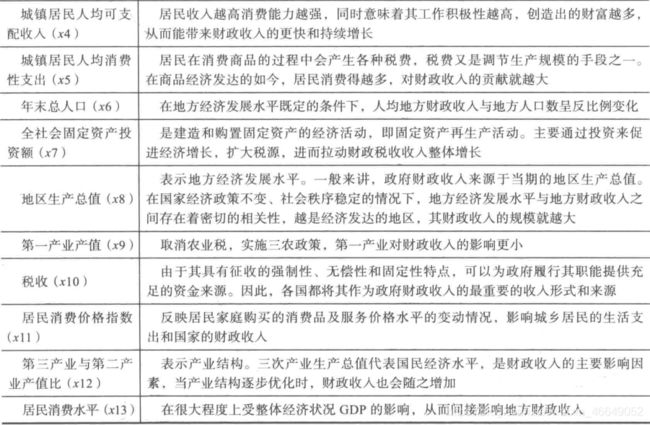
1.数据质量分析
%matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
1.1 缺失值分析
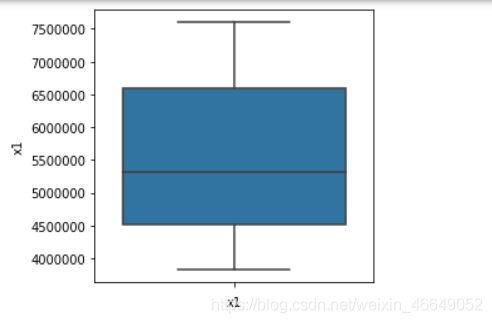
1.2 异常点分析—箱型图分析
for column in data.columns:
fig,ax = plt.subplots(figsize=(4,4))
sns.boxplot(data.loc[:,column],orient='v')
ax.set_xlabel(column)
1.3 重复数据分析
2.数据特征分析
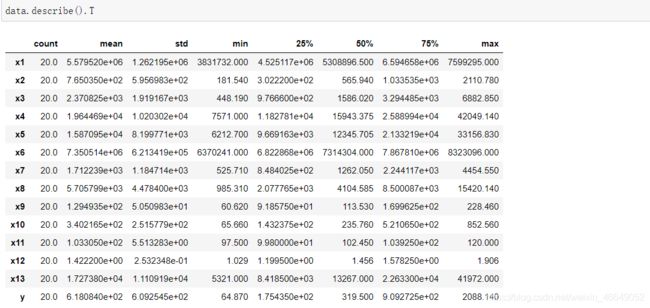
2.1 描述性统计分析
2.2 分布分析
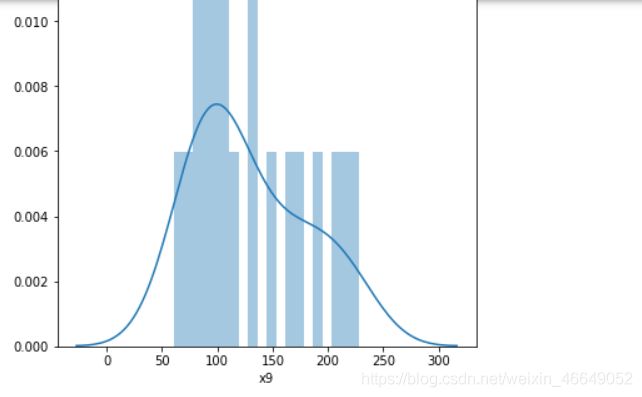
表格里面都是连续型数据,可以通过distplot来展示连续变量的直方图与连续概率密度估计
# 画直方图与连续概率密度估计
for column in data.columns:
fig,ax = plt.subplots(figsize=(6,6))
sns.distplot(data.loc[:,column],norm_hist=True,bins=20)
2.3 相关性分析
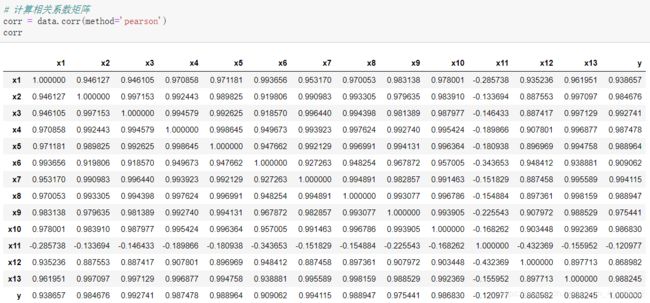
可以发现上述变量除了x11外均与y有强相关性,并且这些属性间存在多重共线性,考虑使用Lasso特征选择模型进行特征选择
绘制相关性热力图,直观显示相关性
# 绘制热力图
plt.style.use('ggplot')
sns.set_style('whitegrid')
plt.subplots(figsize=(10,10))
sns.heatmap(data.corr(method='pearson'),
cmap='Reds',
annot=True, # 诸如数据
square=True, # 正方形网格
fmt='.2f', # 字符串格式代码
yticklabels=corr.columns, # 列标签
xticklabels=corr.columns # 行标签
)
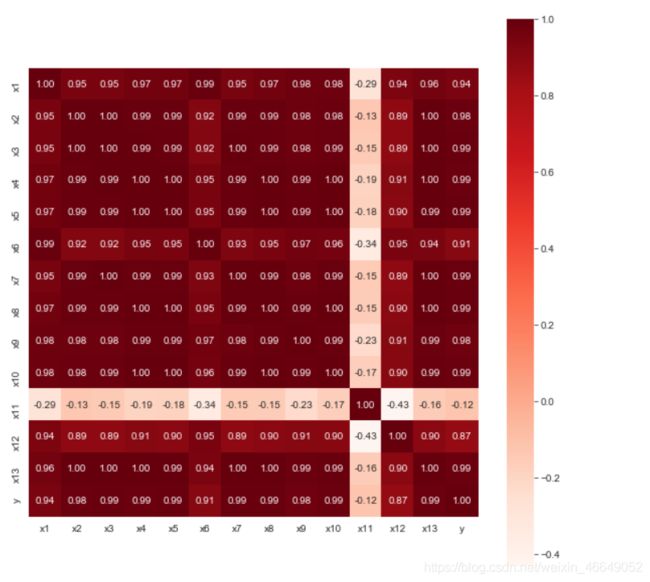
很明显可以看出除了x11外均与y有强相关性,并且这些属性间存在多重共线性。
二、数据预处理
通过上面分析,我们知道数据中没有缺失值、重复值、异常值(数据来源可靠),发现有多重共线性,我们能做的是:利用Lasso特征选择,去除特征间的多重共线性
import pandas as pd
import numpy as np
from sklearn.linear_model import Lasso
data = pd.read_csv('data/data.csv', header=0)
x, y = data.iloc[:, :-1], data.iloc[:, -1]
# 取alpha=1000进行特征提取
lasso = Lasso(alpha=1000, random_state=1)
lasso.fit(x, y)
# 相关系数
print('相关系数为', np.round(lasso.coef_, 5))
coef = pd.DataFrame(lasso.coef_, index=x.columns)
print('相关系数数组为\n', coef)
# 返回相关系数是否为0的布尔数组
mask = lasso.coef_ != 0.0
# 对特征进行选择
x = x.loc[:, mask]
new_reg_data = pd.concat([x, y], axis=1)
new_reg_data.to_csv('new_reg_data.csv')
三、模型构建
1.灰色预测模型
灰色预测算法是一种对含有不确定因素的系统进行预测的方法。在建立灰色预测模型之前,需先对原始时间序列进行数据处理,经过数据处理后的时间序列即成为生成列。灰色系统常用的数据处理方式有累加和累减两种。灰色预测以灰色模型为基础,在众多灰色模型中,GM(1,1)模型最为常用。下面展示灰色预测算法的过程及代码实现
设特征 X ( 0 ) = { X ( 0 ) ( i ) , i = 1 , 2... , n } X^{(0)}=\{X^{(0)}(i),i=1,2...,n\} X(0)={X(0)(i),i=1,2...,n}为一非负单调原始数据序列,建立灰色预测模型如下:
- 首先对 X ( 0 ) X^{(0)} X(0)进行一次累加,得到一次累加序列 X ( 1 ) = { X ( 1 ) ( k ) , k = 0 , 1 , 2... , n } X^{(1)}=\{X^{(1)}(k),k=0,1,2...,n\} X(1)={X(1)(k),k=0,1,2...,n}
- 对 X ( 1 ) X^{(1)} X(1)可建立下述一阶线性微分方程,即 G M ( 1 , 1 ) GM(1,1) GM(1,1)模型
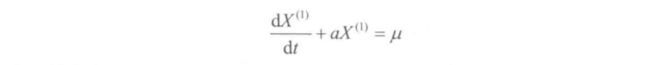
- 求解微分方程,即可得到预测模型
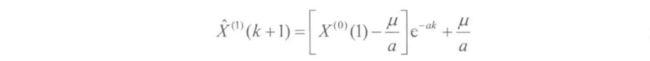
- 由于 G M ( 1 , 1 ) GM(1,1) GM(1,1)模型得到的是一次累加量,将 G M ( 1 , 1 ) GM(1,1) GM(1,1)模型所得的数据 X ^ ( 1 ) ( k + 1 ) \hat{X}^{(1)}(k+1) X^(1)(k+1)经过累减还原为 X ^ ( 0 ) ( k + 1 ) \hat{X}^{(0)}(k+1) X^(0)(k+1),即 X ( 0 ) X^{(0)} X(0)的灰色预测模型
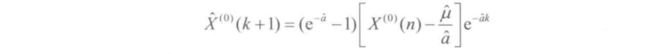
- 后验差检验模型精度

灰色预测法的通用性强,一般的时间序列场合都适用,尤其适合那些规律性差且不清楚数据产生机理的情况。灰色预测模型的优点是预测精度高,模型可检验、参数估计方法简单、对小数据集有很好的的预测效果;缺点是对原始数据序列的光滑度要求很高,在原始数据列光滑性较差的情况下灰色预测模型的预测精度不高,甚至通不过检验,结果只能放弃使用灰色模型进行预测。
利用GM(1,1)灰色预测方法得到关键影响因素在2014和2015年的预测值
# 自定义灰色预测函数
def GM11(x0):
# 数据处理
x1 = x0.cumsum() # 1-AGO序列
z1 = (x1[:len(x1) - 1] + x1[1:]) / 2.0 # 紧邻均值(MEAN)生成序列
z1 = z1.reshape((len(z1), 1))
# 计算参数
B = np.append(-z1, np.ones_like(z1), axis=1)
Yn = x0[1:].reshape((len(x0) - 1, 1))
[[a], [b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Yn)
# 还原值
f = lambda k: (x0[0] - b / a) * np.exp(-a * (k - 1)) - (x0[0] - b / a) * np.exp(-a * (k - 2))
# 后验差检验
delta = np.abs(x0 - np.array([f(i) for i in range(1, len(x0) + 1)]))
C = delta.std() / x0.std()
P = 1.0 * (np.abs(delta - delta.mean()) < 0.6745 * x0.std()).sum() / len(x0)
return f, a, b, x0[0], C, P # 返回灰色预测函数、a、b、首项、方差比、小残差概率
new_reg_data = pd.read_csv('new_reg_data.csv', header=0, index_col=0) # 读取经过特征选择后的数据
data = pd.read_csv('data/data.csv', header=0) # 读取总的数据
new_reg_data.index = range(1994, 2014)
new_reg_data.loc[2014] = None
new_reg_data.loc[2015] = None
cols = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13']
for i in cols:
f = GM11(new_reg_data.loc[range(1994, 2014), i].values)[0]
new_reg_data.loc[2014, i] = f(len(new_reg_data) - 1) # 2014年预测结果
new_reg_data.loc[2015, i] = f(len(new_reg_data)) # 2015年预测结果
new_reg_data[i] = new_reg_data[i].round(2) # 保留两位小数
y = list(data['y'].values) # 提取财政收入列,合并至新数据框中
y.extend([np.nan, np.nan])
new_reg_data['y'] = y
new_reg_data.to_excel('new_reg_data_GM11.xls') # 结果输出
print('预测结果为:\n', new_reg_data.loc[2014:2015, :]) # 预测结果展示
预测完后利用GM11函数中的C、P值进行检验,衡量灰色预测模型的精度
2.构建支持向量机回归模型
使用支持向量回归模型对财政收入进行预测,由于数据量小,就没有设置测试集
from sklearn.svm import LinearSVR
import matplotlib.pyplot as plt
data = pd.read_excel('new_reg_data_GM11.xls',index_col=0,header=0) # 读取数据
feature = ['x1', 'x3', 'x4', 'x5', 'x6', 'x7', 'x8', 'x13'] # 属性所在列
data_train = data.loc[range(1994, 2014)].copy() # 取2014年前的数据建模
# 数据标准化
data_mean = data_train.mean()
data_std = data_train.std()
data_train = (data_train - data_mean) / data_std
x_train = data_train[feature].values # 属性数据
y_train = data_train['y'].values # 标签数据
# 调用LinearSVR()函数
linearsvr = LinearSVR()
linearsvr.fit(x_train, y_train)
x = ((data[feature] - data_mean[feature]) / data_std[feature]).values # 预测,并还原结果。
data[u'y_pred'] = linearsvr.predict(x) * data_std['y'] + data_mean['y']
# SVR预测后保存的结果
data.to_excel('new_reg_data_GM11_revenue.xls')
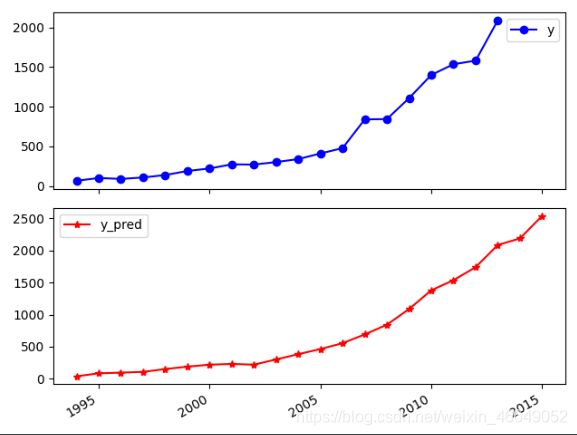
print('真实值与预测值分别为:\n', data[['y', 'y_pred']])
fig = data[['y', 'y_pred']].plot(subplots=True, style=['b-o', 'r-*']) # 画出预测结果图
plt.show()
真实值与预测值分别为:
y y_pred
1994 64.87 39.178714
1995 99.75 85.572845
1996 88.11 96.280182
1997 106.07 107.925220
1998 137.32 152.320388
1999 188.14 189.199850
2000 219.91 220.381728
2001 271.91 231.055736
2002 269.10 220.501519
2003 300.55 301.152180
2004 338.45 383.844627
2005 408.86 463.423139
2006 476.72 554.914429
2007 838.99 691.053569
2008 843.14 842.424578
2009 1107.67 1086.676160
2010 1399.16 1377.737429
2011 1535.14 1535.140000
2012 1579.68 1737.264098
2013 2088.14 2083.231695
2014 NaN 2185.297088
2015 NaN 2535.939620
如果对您有帮助,麻烦点赞关注,这真的对我很重要!!!如果需要互关,请评论或者私信!
![]()