西瓜书重温(五): 神经网络手推版

1. 写在前面

这个系列也有很长时间没更新了， 这段时间经历了实习和找工作的事情，很难静下心来去阅读西瓜书这样的宝书，所以呢，一直搁置。而现在打算借着寒假在家的时间把这个系列接上。虽然这里面的知识比较偏理论，可能给我们的感觉是不太实用，并且写的有些省略，晦涩难懂，对初学者也不是很友好， 但里面有很多重要的思想是我们解决实际问题中会考虑到的，而我之所以想重温一遍，完全是因为兴趣驱动，而这次重温，我也会尽量结合着其他参考资料，对西瓜书的知识作补充，使其连贯，另外就是尝试用更加白话的语言把里面的知识解读重构，这样学习起来应该会舒服一些，当然，也希望能帮助更多的伙伴，在机器学习的路上走的更加悠然，所谓"飘飘乎如遗世独立，羽化而登仙"

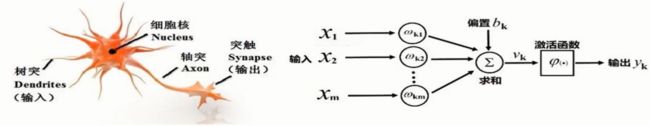
今天复习的是神经网络， 对应西瓜书第五章的内容， 神经网络虽然是机器学习里面的一块，但现在已经慢慢的演化成了一个新的子方向，也就是我们所熟知的深度学习。不过，在西瓜书上的最后面，只是对深度学习简单提了一下子，没有详细展开，我这里同样也不会展开，毕竟这东西涉及的知识点有些多，无法展开整理，后面会单独写几篇文章，整理深度学习的基础知识。

这里的话，依然是以西瓜书的脉络为主，主要对最基础的DNN进行学习， 当然，也结合着其他参考资料做一些补充，让知识更完善，主要包括

• 感知机部分，会补充一些理论证明和公式推导，另外，感知机算法其实是一个非常伟大的算法的， 而西瓜书上太过于粗略，并没有写出感知机的魅力(感知机实际上对于分类问题，找到了一个统一的解决模板)；
• 多层神经网络的反向传播算法公式推导，西瓜书上给我的感觉是符号多，步骤省略，并不太好看，而这块内容往往是公司面试喜欢考的内容
• 有了反向传播算法，就可以用numpy写一个简单的神经网络以及再用熟悉的框架复现一下(这也是公司的面试题)， 所以这块也要补充
• 另外就是对书上说到的前馈网络能逼近任意复杂度连续函数的说法补充个例子感受下
• 其他的，差不多就是这一章里面的一些重要理论知识了，比如遭遇过拟合怎么办， 陷入局部极小怎么办等
• 最后，补充一个面试常看到的一个问题: 神经网络的参数初始化不能是0？ why?

最后， 还想问大家一个灵魂性的问题， 神经网络我们都知道是模拟神经元的一种操作，多种输入对应一种输出， 即所谓的多对一， 多对一我们非常熟悉，像数据结构里面的树， 数学里面的函数都是多对一， 那么既然都是多对一，我们为啥会用神经网络呢？ 换句话说，神经网络的出现应该是具有划时代意义的， 但有没有想过， 为啥是它划时代呢？它究竟好在了哪里？

这篇文章依然是很长，并且涉及到的公式推导由于时间原因依然是手推版(这次尽量写得清晰些)，还是各取所需即可。

大纲如下:

• 神经元模型初识
• 多层神经网络？ 我们先从感知机开始
• 神经网络的前向和反向传播算法公式推导
• 神经网络的numpy版以及tf和pytorch框架的简单实现
• 全局最小和局部极小
• 深度学习初识
• 其他常见神经网络(这一节不是重点，这里直接跳过)
• 补充知识: 神经网络参数不能初始化0的问题理解

Ok, let’s go!

2. 神经元模型初识

神经网络是具有适应性的简单单元组成的广泛并行互连的网络，它的组织能模拟生物系统对真实世界物体做出的反应。 这里的简单单元，指的就是神经网络中的基础成分神经元模型。

1943年， 心理学家W.S.McCulloch和数理逻辑学家W.Pitts基于神经元的生理特征， 建立了单个神经元的数学模型(MP模型)，长下面这个样子：

这个模型中，神经元接收来自$n$个其他神经元传递过来的输入信号， 这些输入信号通过带权重的连接进行传递， 神经元接收到的总输入值与神经元阈值进行比较， 然后通过"激活函数"处理产生神经元的输出。这就是一个神经元在干的事情， 其实这个结构非常简单，是一个典型的多对一结构，又像是数学上的复合函数。而说到多对一，我们又很容易联想到数据结构里面的树结构。

另外，关于这个简单结构，还想扩充两点：

1. 每个输入$x_i$上，都会有一个权重值$w_i$, 我们根据$w_i$的数值往往就能判断出输入对于当前神经元的重要性程度
2. 神经单元里面会有激活操作， 激活函数赋予了神经单元非线性，增强了拟合能力，当然在一个神经单元可能看不出来。这个过程就非常类似于对一个"直男"赋予了更高的情商。 这里的激活函数貌似是用来sigmoid。
   
   把许多这样的神经元按一定的层次结构连接起来，就得到了神经网络。这个基本的神经单元，还有另外一个名字，就是感知机， 要想学习神经网络， 我们应该先聊聊感知机。

3. 多层神经网络? 我们先从感知机开始

3.1 感知机算法(我觉得这是一个伟大的算法)

感知机由两层神经元组成， 是一个二类分类的线性分类模型， 1957年由Rosenblatt提出，是神经网络与SVM的基础。

感知机模型的定义也比较简单， 假设输入空间是$\mathcal{X}\subseteq {\mathbf{R}}^n$， 输出空间是$\mathcal{Y}=\{+1,-1\}$， 输入$x\in \mathcal{X}$表示实例的特征向量， 对应于输入空间中的点， 输出$y\in \mathcal{Y}$表示实例的类别， 由输入空间到输出空间的函数:
$$f(x)=\mathrm{sign}(w\cdot x+b)$$
叫做感知机算法。这里的符号函数，采用的就是上面的阶跃函数。如果我们从几何上去理解，可能就了然了。 首先我们知道线性方程
$$w\cdot x+b=0$$
在二维空间中就是一条直线， 高维空间中对应于超平面$S$， $w$表示法向量， $b$表示截距。 而这个超平面的上方， 就是$w\cdot x+b>0$的点，在超平面的下方，就是$w\cdot x+b<0$， 相当于这条线，能把两类不同的点分成上下两部分。

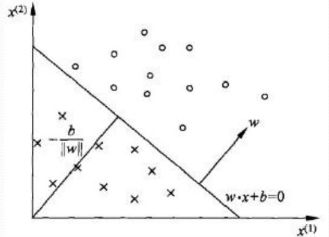
但是呢？ 理解是可以这么理解， 但我们一开始是没有这条直线的， 上面的$w,b$我们是不知道的，感知机算法其实要做的事情，就是事先通过一些已经的训练样本(x,y)， 然后去学习出上面的直线来， 即求出$w,b$来，原来，1957年Rosenblatt大佬就有这种学习的意识了。

那么，应该怎么学习出分割面来呢？ 首先， 先定义损失函数， 既然我们要做二分类问题，那么第一反应，就是希望得到的超平面能正确的把两类样本给分开， 即希望误分类点的个数越少越好， 但这样的损失函数对于$w,b$并不是连续可导的，优化起来会有问题。 所以我们有另外一个选择，即误分类点到超平面的总距离。

这里面两个关键词， 首先是距离， 这个非常简单，就是我们高中所学习的点到直线的距离公式：
$$\frac{1}{\Vert w\Vert }\left|w\cdot x_i+b\right|$$
总距离的话，无非就是所有点的距离之和。那么怎么确定这里的$x_i$是误分类点呢？ 所谓误分类点，就是本身$y_i=1$， 但位于了直线下方($w\cdot x_i+b<0$)或者本身$y_i=-1$， 但却位于了直线上方($w\cdot x_i+b>0$)。 这样其实就看出了规律， 误分类点，是满足这样的公式的:
$$-y_i\left(w\cdot x_i+b\right)>0$$
所以，对于误分类点来说，到直线的距离，可以用下面式子来表示：
$$-\frac{1}{\Vert w\Vert }{y}_i\left(w\cdot x_i+b\right)$$
而这里的$||w||$，是不影响正负的，只是个常数，相当于后面的距离扩大或者缩小多少倍，和正负没有关系。 而后面的梯度下降法关心的是正负， 而不是距离大小。所以可以直接去掉，最终选择的损失函数如下：
$$L(w,b)=-\sum _{x_i\in M}{y}_i\left(w\cdot x_i+b\right)$$
M为误分类点。

显然，损失函数$L(w,b)$是非负的， 如果没有误分类点，损失函数的值是0， 而且，误分类点
越少，误分类点离超平面越近， 损失函数值也就越小。

那么，有了损失函数， 感知机是如何进行学习的呢？ 给定一个训练集
$$T=\{(x_1,y_1),(x_2,y_2),\dots .,(x_n,y_n)\}$$
我们的最优化问题:
$$\underset{w,b}{\min }L(w,b)=-\sum _{x_i\in M}{y}_i\left(w\cdot x_i+b\right)$$
当然这个最优化问题，并不像高等代数上的解析函数那样，一步到位就求出了$w,b$， 而是需要优化迭代， 这里采用的是随机梯度下降算法， 整个过程如下, 这里直接用浙大胡老师PPT里面的一张图了:

这里一定有两点需要说明:

1. 极小化过程中不是一次使M中所有误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降，这也是和SVM那里不同的地方， SVM是直接考虑所有样本点，从全局上进行优化的。 当然， SVM是199几年提出的， 显然是要比感知机算法高级很多的。
2. 随机梯度下降算法真正修改w和b的时候，是应该加一个$\eta$作为学习步长的， 表示超平面向误分类点移动程度， 但感觉上面这个更直观一些。 更好的写法其实是这样:
   $$\begin{array}{rl}\text{if. }{y}_i\left(w\cdot x_i+b\right)& \le 0\\ w& :=w+\eta y_i{x}_i\\ b& :=b+\eta y_i\end{array}$$
   直观上理解这个调整的话：当一个实例点被误分类了，即位于分离超平面错误的一侧时， 下一步调整$w,b$的值， 使分离超平面朝着误分类点那一侧移动，来减少该分类点与超平面的距离，直到超平面越过该误分类点使其正确分类。 当然，这样玩，最终的超平面结果并不是唯一的，和初值以及移动策略有关。

如果感觉上面的移动还不是很明确， 我们可以再进一步， 看看移动了之后到底是什么样子， 这里直接手推一下。

所以，这个移动的策略是合理的， 但此时会不会有个问题， 由于每次选择误分类点都是随机的，那么这样反复的拉来拉去，有没有可能出现不收敛的现象呢？ 感知机算法之所以这么伟大， 其中很重要的一个原因，就是Rosenblatt不仅提出了这样的一个算法， 还亲自证明了，如果样本点线性可分，最后一定能迭代有限的步伐，找到一个把样本点分开的超平面。这可能也是感知机算法被后人认可的一个非常重要的原因了吧。 下面，我们先看看他是怎么证明的，然后呢， 我们不妨再换个角度，感受下感知机算法的伟大之处。

这里依然是手推一下， 首先，我们先对感知机算法流程进行一些简化。

写成向量的方式，仅仅是因为看起来简单。

感知机算法收敛定理是这样:

输入${\left[X_i\right]}_{i=1\sim N}$， 若线性可分， 即$\exists W_{opt}$ 使得
$$W_{opt}^{\top }{X}_i>0(i=1\sim N)$$
则利用上述的感知机算法， 经过有限步之后， 肯定能得到另一个$W$， 使得$$W^{\top }{X}_i>0(i=1\sim N)$$成立。

注意， 后面的$W$并不一定就是$W_{opt}$， 因为如果一个超平面能把两类样本分开，那么一定存在无数个这样的超平面， 所以这俩相等的概率非常小。 但如果可分，一定能找到一个超平面把这两类样本分开。

下面看具体证明。

当然，上面是定性的分析，如果进行定量的分析，

也就是说，只要一直存在误分类的点， 也最多只需要经过$D^2$， $W$就会收敛至$a{W}_{opt}$， 而$W_{opt}$是能把两类样本分开的超平面。 所以，如果样本可分， 利用感知机算法，是肯定能在有限步收敛到解的(当然不一定是最优解)， 但至少能解决线性可分样本二分类问题了。

我觉得感知机算法也是一个伟大的算法，当然数学上可能不如SVM那么漂亮，但Rosenblatt大佬的这个证明思路也是很漂亮的， 大佬之所以称为大佬，可不仅仅提出了某个算法， 还能通过数学证明使得自己算法的体系自洽，这个是非常厉害的。

那么，我们可以再开下脑洞，想一下感知机提出来的意义在哪里呢？ 所谓的分类超平面，不就是个函数吗，既然符合函数定义了，为啥还必须提出个感知机的概念？

分类超平面， 虽然是个函数， 但一定不是解析函数，因为定义域可以无穷多，但值域只有两个(1和-1)， 所以即使是函数， 那肯定也是一个分段函数，不同的定义域下，可能对应不同的函数表达。

所以，即使是函数，但这个函数是没有一个统一的表达的， 那对于一个分段函数求解，就比较麻烦了， 三个非常头疼的问题， 分多少段？ 怎么分段？ 每一段怎么解？

这还是面临一个二分类问题， 而换一个二分类问题， 又得重新考虑上面三个问题。

所以， 我们所谓的函数表达式， 其实并不能统一解决现实世界里面的二分类问题。

于是，面对线性可分二分类问题，最主要的是找一个统一模板， 凡是这类问题， 这个模板都是有效的， 而感知机， 在这里就体现了价值。

Rosenblatt老爷子就说， 我提出的这个算法只需要一些输入输出对(x,y)， 然后算法可以自己学习，最终求出超平面，解决这个问题，并且只要是线性可分的问题，一定能找到这样的超平面。

那么，这不就是我们所说的模板吗？ 只要我们的问题是线性，二分的， 都可以照着感知机的模板表示出来，感知机不仅确定了这样的模板存在，还确定了这样的模板长什么样。

如果是直接分类，那么这个函数可能是不连续的，或者稀奇古怪的。 但是呢？ 只要通过感知机， 都最终能统一表达成一个线性函数+激活函数的方式。 线性函数简单，激活函数简单，这俩简单的东西，结合感知机学习算法，竟然能把非常复杂的东西表达出来。我觉得，这才是感知机的真正魅力所在。

如果你说，感知机这玩意学习能力非常有限， 貌似是连最简单的异或问题都解决不了，这有啥用？首先，异或问题是非线性可分问题， 一个感知机解决不了是正常的， 但一个不行， 我们可以来两个感知机， 两个感知机不行， 可以三个… 而这，就形成了我们所说的神经网络。

万能逼近定理：只需要一个包含足够多神经元的隐藏层， 神经网络就能以任意精度逼近任意复杂度的连续函数。

这个万能逼近定理， 在后面的实现完神经网络之后，也会举个例子直观感受下， 但我们可以想一下， 万能逼近， 我们在其他地方是不是也见到过呢？ 知识串联， 我脑海中浮现出了泰勒和傅里叶的身影， 我们高数上学习到的函数的泰勒展开， 傅里叶级数(一个复杂的函数可以拆解成一个个圆周运动或者正弦波)， 是不是都是化复杂为简单的思路？

3.2 从感知机到神经网络

在感知机的那个年代， 其实还没有线性可分和线性不可分的概念， 后来是明斯基大佬("人工智能"之父)在1969年的时候创造了这个概念。

1969. Minsky《Perceptron》一书，日常生活中很多分类问题是非线性可分的。

西瓜书上举了一个最简单的例子，也就是经典的异或问题。

异或问题我们是无法找到一条直线，能把两个类别完全分开的。

感知机连这么简单的问题都解决不了，所以接下来的一段时间，人们又对感知机失去了希望， 这也迎来了人工智能的"第一次寒冬"， 到了19世纪80年代初，有人提出了多层的神经网络算法， 使得这种问题有了一定的缓解， 人工智能迎来另一个春天。

1986年， Hinton老爷子等人提出了反向传播(BP)算法，使得多层神经网络的训练更为简单， 神经网络再一次活了起来。

解决上面的异或问题，我们就可以用两个感知机

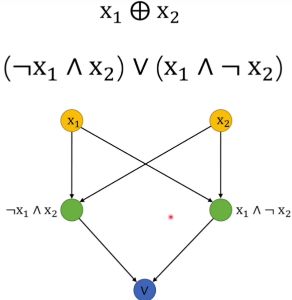
即输入$x_1,x_2$先分别过两个感知机， 然后这两个感知机的输出，然后再把这两个感知机的输出再重新当做输入再过一个感知机得到最终的分类结果，这样才能实现异或运算。整个过程，相当于将原来的输入$x_1,x_2$先分别做两次线性变换，得到$a_1,a_2$， 然后把$a_1,a_2$再当做输入做一次线性变换得到$y_1$。

这其实就是一个最简单的2层神经网络， 其中中间的一层叫做隐藏层， 最后的一层叫输出层， 最上面的一层叫输入层， 这是一个单隐层神经网络，当然还有多隐层的：

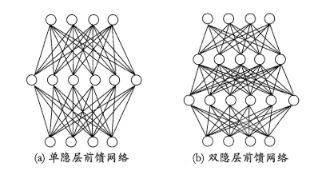
输入层神经元接收外界输入，隐层与输出层神经元对信号加工，最终结果输出层神经元输出。神经网络的学习过程， 就是根据训练数据调整神经元之间的"连接权重"以及每个功能神经元之间的阈值。

多层神经网络可以理解成是把一个复杂的函数， 拆解成一个个的感知机(一个线性函数+一个激活函数)

下面我们具体看看多层神经网络的一些细节。

4. 多层神经网络

4.1 多层神经网络初识

关于感知机的缺陷，以及为啥会用到多层神经网络上面已经进行了一些铺垫， 这一块的话，主要是解决两个问题， 第一个问题是多层神经网络里面的激活函数为什么是必须的？ 第二个问题是上面万能逼近定理这里需要直观感受下。

关于第一个问题， 多层神经网络里面的激活函数是必须要有的，因为如果没有了激活函数， 多层神经网络的效果其实可以用一层的神经网络等效， 并且关键的是，这样的网络依然是个"直男"， 不能进行非线性拟合。 我下面从前向传播的角度进行了手推，理性感受一下：

这里我简单的画了一个两层的神经网络， 这个也是后面推前向和反向传播用的例子， 输入层两个神经元，接收输入$x_1,x_2$， 接着过一个隐藏层，这个隐藏层3个神经元， 接着是接一个输出层，这个2个神经元， 得到$y_1,y_2$， 最后是$y_1,y_2$跟一个sortmax计算，得到最后输出，这个转换成了概率，可以先不用管。 后面推前向和反向传播公式的时候具体写。

这里拿了$y_1$计算举例， 左边是正常神经网络$y_1$计算公式， 右边是去掉了隐藏层激活函数(这里默认用了sigmoid)的计算公式， 可以发现如果去掉了激活函数， 最终化简之后， 依然是一个输入的线性组合， 而这个线性组合等效为一个一层的神经网络。

第二个问题，就是上面的万能逼近定理，浙大的胡老师用了例子直观的进行了解释，这里也手绘了下

那么这里就有一个问题了，理论上不是三层神经网络就可以模拟所有决策面吗？ 那为什么我们看到的多层神经网络往往是很多个层？ 其实， 这里的万能逼近， 依然是一个理想状态， 因为我们真实神经网络的参数，并不是人为指定， 而是通过有限的数据样本去学习的。事实证明， 对于一个复杂的界面， 用多层的神经网络分块进行模拟， 要比用一层神经网络(可能无限个神经元)效果要好的多， 并且在训练上要容易， 毕竟只有一层，假设无限个神经元， 而样本是少量， 那么这个参数学习起来超级复杂。 这也是为啥万能逼近定理没法在实际中使用的原因。

这个东西我觉得是为了让我们感受下神经网络的强大性， 三层的神经网络都能理论上模拟所有决策面， 那如果把复杂的决策面分块，然后用多层的简单神经网络去模拟， 那么不就更简单。

这里感觉有点分治的意思了， 对于一个超级复杂的问题， 通过分块， 可以用简单的多层网络去解决， 而多层网络呢？ 可以通过再分块，用一个个更简单的感知机去解决，最后汇总起来，就搞定了大问题。

我们知道了多层网络的学习能力要比单层感知机强得多，那么，如何训练这个"庞然大物"呢？ 简单的感知机学习规则就远远不够了， 所以， 这里采用了更强大的学习算法误差逆传播(errorr BackPropagation, BP)算法， 这个目前依然被使用。

所以学习神经网络的数学原理， 很重要的一块，就是这个反向传播算法的推导， 也就是神经网络究竟是如何学习的，下面就进行手推一下。

4.2. 前向和反向传播算法公式推导

这里先初识下反向传播算法：

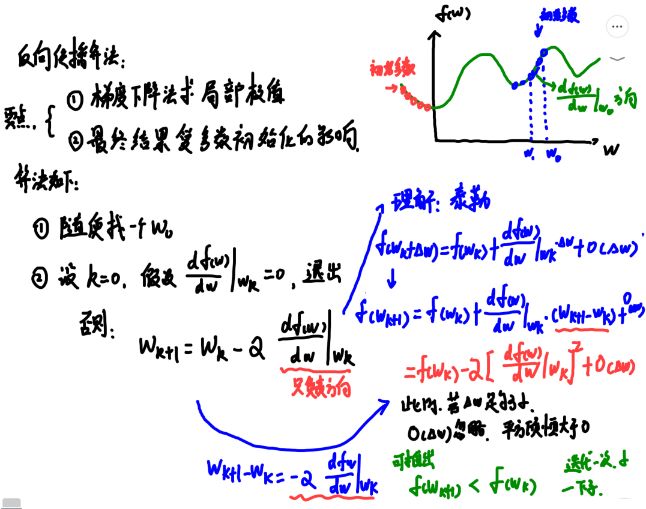
这个是西瓜书上104页反向传播算法的提炼版， 那里的步骤，首先是初始化所有参数， 然后给定输入后，先正向传播计算输出$y$，得到损失函数。 请注意，我们这里要明确网络的优化问题， 是通过调节神经网络层的各种参数，使得最终的损失函数最小， 所以这里的$f(w)$指的是最终损失函数。

计算出$f(w)$来， 然后再通过链式法则反推出每一层参数的导数$\frac{df(w)}{d{w}^k}$， 就能通过上面的更新公式，更新每一层的参数了。

这里先拿上面简单的三层神经网络推一下， 然后扩展到多层的情况， 这里和西瓜书上不一样的地方，是损失函数的计算采用了softmax， 而不是用平方差损失， 因为这里想学习下softmax函数公式推导和计算， 平方差损失之前推导过，这里换个新的。

1. 针对多分类问题(softmax输出，所有输出概率和为1)
   $$H=-\sum _i{o}_i^{\ast }\log \left(o_i\right)$$
2. 针对二分类问题(sigmoid输出，每个输出节点之间互不相干)
   $$H=-\frac{1}{N}\sum _{i=1}^N\left[o_i^{\ast }\log o_i+\left(1-o_i^{\ast }\right)\log \left(1-o_i\right)\right]$$

再简单记录下这俩的区别：如果是softmax输出， 这里的输出会满足一个和为1的分布。 而如果是二分类的sigmoid输出， 这里的分布就没有限制了

• 如果是做一个猫狗分类， 得到的输出要么是猫，要么是狗， 这两个满足概率就是一个和为1的分布。这时候就用一个softmax输出。
• 如果是做一个判断是不是男人的分类器， 那么输出就有可能是人类， 有可能是男人， 也就是输出可能不满足和为1的分布，人类有可能包含男人了，这时候就需要使用sigmoid输出。

正向传播如下:

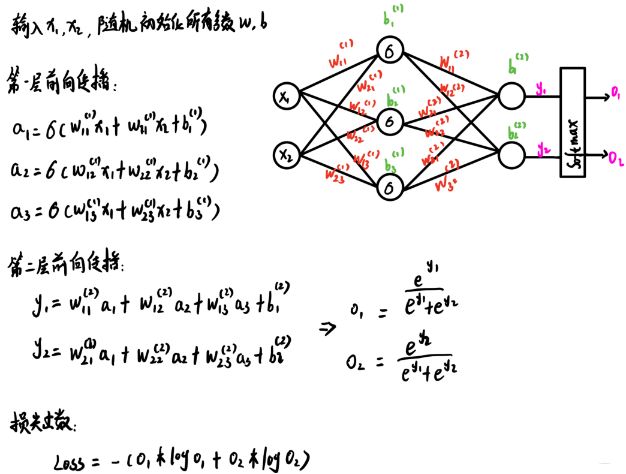
根据上面的公式，输入一个训练样本$\{(x_1,x_2),label(o_1^{\ast },o_2^{\ast })\}$这里的label一般是经过了one-hot， 就能得到一个损失值。上面损失函数的*符号应该是右上标星号，不是乘，下面图里重新写了遍。

下面看通过这个样本之后，神经网络如何更新参数， 即关键的反向传播:

再往前一层:

这里后向传播的意思是， 计算梯度的时候， 是从后面往前面一步步通过链式法则算的。这个更简单的理解，就类似于下面的这种公式
$$y=f(g(h(l(m(x)))))$$
正向的时候，从里面一层层的往外算， 而计算导数的时候， 就需要从外面一层层的往里算了。

另外一个需要注意的是， 这里是西瓜书上说的那种"标准BP算法"， 也就是每次针对一个训练样本进行的参数更新，而实际情况中， 往往是最小化训练集上的累积损失误差，这叫做"累积BP算法"

一般来说，标准BP算法每次更新只针对单个样例， 参数更新非常频繁， 而且不同样例参数更新可能会出现"抵消"现象。 因此，为了达到同样的累积误差极小化， 标准BP算法往往需更多迭代次数。 但这种方法在训练集非常大的时候，速度更快。

这俩的区别，就类似于随机梯度下降(SGD)和梯度下降的区别

这就是一个三层神经网络的反向传播算法细节了， 再多层数的神经网络也是一个道理， 这个就在这里不整理了， 我直接用当时学习吴恩达老师深度学习时候课程笔记了，吴恩达老师讲的这里并没有上面这么细， 稍微简单些，并且使用了向量化的版本。 但有了上面这个细的版本，再看多层以及向量化版本的就非常容易了。

多层神经网络的前向传播与向量化：

多层神经网络反向传播与向量化：

5. 神经网络搭建

这里就动手小实践下， 先用numpy实现一个简单的小神经网络，然后尝试用tf和Pytorch框架对其替换，令训练更加高效。 但是， 能用numpy实现底层的前向传播和反向传播还是有必要的，毕竟这是基本功。

由于上面那个网络计算梯度太麻烦了， 这里就打算用一个稍微简单些的网络， 前向传播和反向传播我都已经计算好了。

5.1 numpy实现神经网络

这个网络，如果用numpy写的话， 可以写成如下代码:

# 定义样本数，输入层，隐藏层，输出层的参数
N, D_in, H, D_out = 64, 1000, 100, 10

# 创造训练样本x,y  这里随机产生
x = np.random.randn(N, D_in)
y = np.random.randn(N, D_out)

# 随机初始化参数w1， w2
w1 = np.random.randn(D_in, H)
w2 = np.random.randn(H, D_out)

# 下面就是实现神经网络的计算过程
learning_rate = 1e-6
epochs = 500
for epoch in range(epochs):
	# 前向传播
	h = x.dot(w1)
	h_relu = np.maximum(h, 0)
	y_pred = h_relu.dot(w2)
	
	# 计算损失
	loss = np.square(y_pred-y).sum()
	print(epoch, loss)
	
	# 反向传播
	# w2的梯度
	grad_y_pred = * (y_pred-y)
	grad_w2 = h_relu.T.dot(grad_y_pred)
	# w1的梯度
	grad_h_relu = grad_y_pred.dot(w2.T)
	grad_h = grad_h_relu.copy()
	grad_h[h<0] = 0
	grad_w1 = x.T.dot(grad_h)
	
	# 更新参数
	w1 -= learning_rate * grad_w1
	w2 -= learning_rate * grad_w2

这里本来想尝试用numpy手撸一个可以自定义很多层的这种神经网络， 这种实现的时候，需要用参数字典保留正向传播的中间值， 反向传播的时候会用到，另外一个要注意的是反向传播实现的时候， 每一层输出的梯度也要算出来，这个是关键节点， 需要保存起来。 具体代码如下:

class DNN_Model:
    def __init__(self, input_dim, layer_units=[1000, 100, 10], alpha=0.001):
        self.input_dim = input_dim
        self.layer_units = layer_units
        self.layer_nums = len(layer_units)
        self.alpha = alpha
        # 参数列表
        self.params_dict = defaultdict(dict)
        self.gradient_dict = defaultdict(dict)
        
        self.init_params()
    
    # 参数初始化
    def init_params(self):
        # 先生成一个邻居对列表，比如[1000, 100, 10] -> [(1000, 100), (100, 10)]
        self.neighbors = list(zip(self.layer_units[:-1], self.layer_units[1:]))
        # 遍历层数进行初始化
        for layer_num, unit_num in enumerate(self.neighbors):  # 0, 1
            self.params_dict[layer_num+1][f'w_{layer_num+1}'] = np.random.rand(unit_num[0], unit_num[1])
            self.params_dict[layer_num+1][f'b_{layer_num+1}'] = np.zeros((self.input_dim, unit_num[1]))
    
    # 前向传播
    def forward(self, X):
        self.params_dict[1]['h_relu_0'] = X
        for layer_num in range(self.layer_nums-1):  # [(1000, 100), (100, 10)]  1， 2层
            if layer_num < self.layer_nums - 2:
                h = X.dot(self.params_dict[layer_num+1][f'w_{layer_num+1}'])
                h_relu = np.maximum(h, 0)
                self.params_dict[layer_num+2][f'h_relu_{layer_num+1}'] = h_relu  # 第二层的输入是第一层的输出
            else:
                y_pred = self.params_dict[layer_num+1][f'h_relu_{layer_num}'].dot(self.params_dict[layer_num+1][f'w_{layer_num+1}']) #+ self.params_dict[layer_num+1][f'b_{layer_num+1}']
                
        return y_pred
    
    # 计算损失
    def comput_loss(self, y_pred, y):
        return np.square(y_pred, y).sum() * 1/2
    
    # 反向传播
    def backward(self, y_pred, y):
        grad_y_pred = y_pred - y    # [64, 10]
        
        for layer_num in range(self.layer_nums-1, 0, -1):  # 2, 1
            # 最后一层
            if layer_num == self.layer_nums-1:
                grad_h_relu = grad_y_pred.dot(self.params_dict[layer_num][f'w_{layer_num}'].T)
                grad_w = self.params_dict[layer_num][f'h_relu_{layer_num-1}'].T.dot(grad_y_pred)
                grad_b = grad_y_pred
                self.gradient_dict[layer_num][f'grad_w_{layer_num}'] = grad_w
                self.gradient_dict[layer_num][f'grad_b_{layer_num}'] = grad_b
                self.gradient_dict[layer_num][f'grad_h_relu_{layer_num-1}'] = grad_h_relu
            else:
                grad_h_relu = self.gradient_dict[layer_num+1][f'grad_h_relu_{layer_num}']
                grad_h = grad_h_relu.copy()
                grad_h[grad_h<=0] = 0
                grad_h[grad_h>0] = 1
                
                grad_h_relu = grad_h.dot(self.params_dict[layer_num][f'w_{layer_num}'].T)
                grad_w = self.params_dict[layer_num][f'h_relu_{layer_num-1}'].T.dot(grad_h)
                grad_b = grad_h
                self.gradient_dict[layer_num][f'grad_w_{layer_num}'] = grad_w
                self.gradient_dict[layer_num][f'grad_b_{layer_num}'] = grad_b
                self.gradient_dict[layer_num][f'grad_h_relu_{layer_num-1}'] = grad_h_relu
                
    # 更新梯度
    def update_gradient(self):
        for layer_num in range(self.layer_nums-1):
            self.params_dict[layer_num+1][f'w_{layer_num+1}'] -= self.alpha * self.gradient_dict[layer_num+1][f'grad_w_{layer_num+1}']
            self.params_dict[layer_num+1][f'b_{layer_num+1}'] -= self.alpha * self.gradient_dict[layer_num+1][f'grad_b_{layer_num+1}']

这个简单看看即可， 知道大致上怎么传的，真实用的时候，现在都是有现成的网络， 好处是反向传播非常简单，梯度都会帮我们计算好。 因为上面求梯度的过程非常容易出错。 我上面代码貌似就有错误，debug了半天也没查出来。但流程的话基本上是这个流程。

下面看看用框架实现神经网络，然后完成这个任务。

5.2 tf框架搭建神经网络

理论上应该用model接口实现， 我这里为了简单，直接keras搭建了， 这个很简单：

model = tf.keras.Sequential([
    tf.keras.layers.Dense(1000, activation='relu', input_shape=(1000,)),
    tf.keras.layers.Dense(100, activation='relu'),
    tf.keras.layers.Dense(10, activation='sigmoid')
])
model.compile(optimizer=tf.keras.optimizers.Adam(),
              loss=tf.keras.losses.mse,
              metrics=['accuracy'])
history = model.fit(x, y, batch_size=64, epochs=100, verbose=1)

5.3 Pytorch框架神经网络

Pytorch搭建神经网络也同样比较简单：

# 我们定义一个两层的神经网络类，这个继承与nn.Module模块
class TwoLayerNet(torch.nn.Module):
	# 定义成员层
	def __init__(self, D_in, H, D_out):
		super(TwoLayerNet, self).__init__()
		self.linear1 = torch.nn.Linear(D_in, H)
		self.linear2 = torch.nn.Linear(H, D_out)
	
	# 定义前向传播
	def forward(self, x):
		h_relu = self.linear1(x).clamp(min=0)
		y_pred = self.linear2(h_relu)
		return y_pred

# 这样就定义了一个二层神经网络的类
N, D_in, H, D_out = 64, 1000, 100, 10

x = torch.randn(N, D_in)
y = torch.randn(N, D_out)

# 定义一个模型
model = TwoLayerNet(D_in, H, D_out)

# 开始计算神经网络
criterion = torch.nn.MSELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr=1e-4)

for it in range(1):
    # 前向传播
    y_pred = model(x)

    # 计算损失
    loss = criterion(y_pred, y)
    print(it, loss)

    # 反向传播, 更新参数
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

这节最后，整理西瓜书上提到的策略性的知识，神经网络如何缓解过拟合：

一种策略是早停: 将数据分成训练集和验证集， 训练集用来计算梯度， 更新权重， 验证集用来估计误差， 若训练集误差降低但验证集误差升高， 则停止训练，返回具有最小验证集误差的权重

另一种策略是正则化

当然，现在还有其他的一些策略了，比如多加数据， 集成学习的思路等

6. 全局最小和局部极小

神经网络很容易陷入局部最优解，这里可以直观感受全局和局部最优:

这个和初始化的参数有很大关系，西瓜书上也给出了一些策略来跳出"局部极小"：

• 用多组不同参数值初始化多个神经网络， 按标准方法训练后， 其中误差最小的解作为最终参数，相当于从不同初始点开始搜索
• 模拟退火技术
• 使用随机梯度下降， 在计算梯度时加入了随机因素， 这个是常用的

7. 深度学习初识

这一块西瓜书上并没有说太多， 我这里也不打算整理太多，因为现在深度学习算是一个以多层神经网络为代表的大分支了，并且根据任务不同， 神经网络也变得多种多样， 比如CV领域的卷积神经网络， NLP中的循环神经网络等。领域很大，我也正在学习中，所以后面就分开领域慢慢整理深度学习的知识了。 详情可以见cv，推荐以及nlp等学习笔记专栏吧。

神经网络模型， 提高容量的一个简单方法是增加隐层的数目， 西瓜书上也提到，增加隐藏层的数目显然比增加单层神经元个数有效， 因为增加隐藏数目不仅增加了拥有激活函数的神经元数目，也增加了嵌套的层数。

里面还提到了无监督，迁移学习， 权共享技术等， 这些现在也都是很火的一些知识了，后面还单独写了点卷积神经网络的知识， 但这些东西后面打算写到cv专栏，单独用文章整理，这里就不过多整理了。

8. 补充知识: 神经网络参数不能初始化0的问题理解

最后， 补充一个问题， 就是神经网络的参数一般不能初始化为0， 这是为啥？ 这里其实还能更深的看一看。

首先， 我们先分析最简单的逻辑回归， 我这里手推了下前向和反向传播：

逻辑回归的话，但参数初始化为0的时候， 此时权重是可以得到更新的。

下面看看多层的神经网络:

看上面的公式

1. 若$w$初始化0， $b$初始化0

   • 前向传播: $a_1=g(0),a_2=g(0),a_3=sigmoid(0)$
   • 反向传播: $a_1=a_2=>d{w}_{13}=d{w}_{23}$， 更新时$w_{13}=w_{23}$， 权重对称性

   
   由于$w$初识为0， 在第一个batch反向传播是导致$d{a}_1=d{a}_2=0$， 即第一个batch除$w_{13}$和$w_{23}$以及$b_3$能得到更新，其他权重得不到更新， 第二个batch传给神经网络，由于$w_{13},w_{23}$相等不为0， 会导致$d{a}_1,d{a}_2$相等，导致$w_{11}=w_{12},w_{21}=w_{22}$。 依次类推， 无论训练多少次， 无论隐藏层神经元多少个， 由于权重对称性，同一隐层所有神经元输出一致。这种情况会出现隐层神经单元输出对称性， 神经网络意义就是不同神经元学习不同信息， 所以如果初始化为0， 多个神经元就如同一个神经元了，但注意，并不是说参数不能更新。

2. $w$初始化为0， $b$随机初始化

   • 第一个batch前向传播:$a_1=g(b_1),a_2=g(b_2),a_3=sigmoid(b_3)$
   • 反向传播: 由于$d{a}_1$与$d{a}_2$均为0， 导致$d{w}_{11},d{w}_{12},d{w}_{21},d{w}_{22}$为0， 则$w_{11},w_{12},w_{21},w_{22}$得不到更新， 为0。

   
   模型能更新的只有$w_{13},w_{23},b_3$， 同理，第二个batch， 由于$w_{13},w_{23}$不是0了，导致所有参数都能得到更新， 这种方式更新较慢， 梯度消失和爆炸问题，实践中往往不采用， 但注意， 此时网络是能正常训练的。

另外， 上面这个结论是基于激活函数是sigmoid的情况下，如果换成tanh或者relu， 如果权重都为0， 就无法更新参数和训练了。

所以最终结论:

1. 神经网络权重如果初始化为0， 这样会导致同一隐层的神经单元输出一致， 参数更新全部一致， 从而出现对称性， 使得多个神经元的作用和一个神经元一致，发挥不出神经网络的威力
2. 但并不是网络参数不更新， 网络的参数是可以更新的， 反向传播更新次序：
   1. 第一次，最后一层权重更新， 前面权重不更新(0)
   2. 第二次，最后一层和倒数第二层更新， 前面为0…
   3. 依次往前
3. 单层逻辑回归是可以初始化全0的
4. 如果激活函数不是sigmoid， 换成别的，上面结论不成立了，而是无法更新梯度了

最后一点， embedding层的参数是可以初始化为0的， 这是因为embedding层参数利用的时候是各种不同的$embeddin{g}_i$的交叉组合，即不同的$embeddin{g}_i$和$embeddin{g}_j$交叉时走的不同的网络单元，这时候是能够正常更新的。

这里会发现，不同神经元组合不同， 会打破之前的那种神经元对称性。

神经网络参数初始化随机，一般是用$(-\frac{1}{\sqrt{d}},\frac{1}{\sqrt{d}})$初始化，$d$是该层神经元的个数。

9. 小总

这篇文章到这里终于结束了， 拖拖拉拉的写了很长时间， 发现这东西一旦中途停了， 就不是很愿意再回来写，所以后面给的教训就是，如果要开始，就必须尽快写完它， 这种关联性很强的文章， 适合用连贯的时间写，而不是并行，每天拿点时间挤牙膏。 当然， 做事情还是有些拖延。 哈哈。

下面简单总结下吧， 这篇文章用了大量的篇幅来写神经网络， 从感知机开始推导过来，感知机感觉是一个非常伟大的杰作， 把非常复杂的事情，用简单的理论给统一解决了。

感知机最大的价值，就是给了二分问题的一个套路， 但凡遇到二分问题， 最后都能被感知机拆分成一个线性函数+一个激活函数的形式。

下面我们给感知机的这两部分， 赋予现实意义：

• 线性函数：理解成是对某个类型里面标准模型的描述，比如我们识别猫的时候，对猫的标准模型怎么描述呢？ 就是线性函数了
• 激活函数： 判断的标准， 判断你给的新数据，到底符合不符合这个标准。

另外一个伟大的杰作，就是反向传播算法， 使得多层神经网络使用成为了可能。

神经网络，是经历过许多次描述+判断的过程， 每经过一个神经元，就需要进行描述，然后判断， 然后把判断的结果，输入到下一层神经元。

所有线性函数的集合，就是神经网络对识别问题的标准模型(比如识别猫)的一个描述， 而所有激活函数的集合，就是判断数据到底符合不符合神经网络描述出来的模型。靠着层层的逼问， 最后把二分类问题描述清楚了

神经网络和感知机在某种程度上价值是一样的，都是把复杂的， 用人的理性难以描述的问题，变得能被描述了。而且还能通过增加神经元的方式，让这个描述能无限的逼近真相

如果说线性函数为神经网络提供了描述世界的世界观的话， 那么激活函数就为神经网络提供了描述世界的价值观

这里面用了很多图片，描绘了前向传播和反向传播的公式， 目的是更加细致的理解神经网络的工作原理， 实际使用中， 都有现成的框架实现复杂网络。最后一个初始化为0的问题，也是面试喜欢问的问题， 也是面试喜欢问的问题。

OK， 终于把这个尾巴解决了，后面尝试更新的快一些， 后面就到了贝叶斯了，涉及到有意思的概率了， 这一块也是一直想学，但是没有学习的东西，抓紧去学习和总结，哈哈。

参考:

• 《机器学习》 - 周志华
• 《统计学习方法》 - 李航
• 《深度学习课程》 - 吴恩达
• 机器学习—浙江大学研究生课程
• 第2章 - 感知机笔记
• 深度学习笔记-浅层神经网络
• 什么是感知机？ 它的什么缺陷让人工智能陷入了第一次寒冬