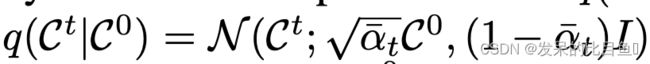2022 ICLR | Geodiff:分子构象几何扩散生成模型

2022 ICLR | Geodiff:分子构象几何扩散生成模型

温馨提示，扩散模型公式比较复杂，若没有基础可以先参考blog或者deep_thoughts老师的视频

本文是由蒙特利尔学习算法研究所唐建团队于2022 ICLR 发表的一篇论文。在这篇论文中，作者受热力学粒子扩散模型的启发，提出了新的生成模型GEODIFF。GEODIFF将每个原子视为一个粒子，并学会直接逆转扩散过程。在多个基准上的实验表明，GEODIFF优于或可与现有的最先进的方法相媲美，特别是在大分子上。作者还在理论上证明了具有等变马尔可夫核的马尔可夫链可以设计出不变分布，并进一步提出了马尔可夫核的构造块来保持理想的等方差特性。

目前方法存在的问题

目前的方法主要通过利用中间几何变量(如原子距离、键和扭转角)来避免直接建模原子坐标，这些中间几何变量是旋转平移不变量。 因此，他们能够实现非常引人注目的性能。然而，由于所有这些方法都寻求间接建模中间几何变量，它们在训练或推理过程中都有固有的局限性。因此，理想的解决方案仍然是直接建模原子坐标，同时考虑旋转平移不变性。

作者思路
作者从理论上证明了由旋转平移不变先验分布出发，以旋转平移等变马尔可夫核演化的马尔可夫过程可以诱导出旋转平移不变密度函数。进一步提供实用的参数化来定义旋转平移不变先验分布和强加等方差约束的马尔可夫核。此外，还导出了分子构象条件似然的一个加权变分下界，该下界同时具有旋转平移不变性，可以有效地优化。

该方法有几个关键的优点：

• 模型可以自然地进行端到端训练，而不涉及任何复杂的技术
• 避免了任何中间误差的积累，因此可以得到更准确的结构预测
• 模拟复杂构象分布方面具有较高的能力

模型

分子构象生成任务本质上是条件生成问题，作者的目标是对于给定的分子图G生成稳定的分子构象C。

图1:GEODIFF扩散和反向过程示意图

扩散过程

根据固定的方差$\beta ,....,{\beta }_T$将其定义为马尔可夫链

其中β是固定的数值, 其时间步t条件概率的近似形式：

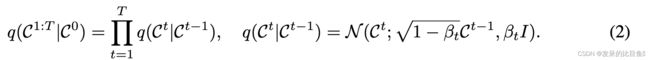
逆扩散过程

从噪声粒子$C^{T}p(C^T)$开始， 给定特定的分子图$g$， 目标是学习从白噪声$C^T$中恢复构象$C^0$。

等变反向生成过程

建立对旋转和平移变换不变的密度$p_{\theta }(C^0)$, 形式上，设$T_g$为元素$g\in SE(3)$的旋转平移变换，得到如下表述
Proposition 1.

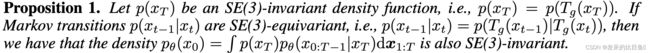
这命题表明，从不变的标准密度出发，沿着等变高斯马尔可夫核的动力学可以产生不变的密度。在此基础上，给出了一种实际的基于扩散去噪框架的GEODIFF算法

Invariant Initial Density
在这种情况下，各向同性高斯显然是围绕zero CoM的旋转的不变性。通过考虑CoM-free系统，将粒子移至zero CoM可以始终确保转化不变性。

Equivariant Markov Kernels
CoM-free高斯函数保证了马尔科夫核的平移不变性。因此，为了实现命题1中定义的等变性质，只关注旋转等方差。

因此，为了保证${\mu }_{\theta }(g,C^t,t)$是旋转-平移等变的$w.r.t{C}^t$。作者考虑${\mu }_{\theta }$的以下参数化:

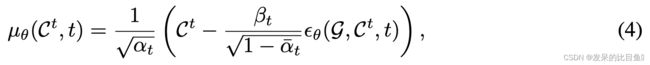
将问题转化为构造${ϵ}_{\theta }$为旋转平移等变,GFN以节点嵌入$h^l\in R^{n\times b}$(b为特征维数)和对应的坐标嵌入$x^l\in R^{n\times 3}$为输入，输出$h^{l+1}$和$x^{l+1}$如下

改进的训练目标

在生成过程和模型参数化之后，开始反向训练目标。由于直接优化对数似然是很困难的，通常做法是最大化变分下界((ELBO)。

下面是公式4的参数化形式：

为了使得ELBO过程具有所需要的等变性，作者提供两种方式修正观测噪音信号。第一种是alignment方式，还有一种chain-rule的方式。

采样

下面是整个采样过程的伪代码。它逐渐地将先前的噪声位置移向平衡态，采样过程本质上是马尔可夫链。

数据集

• GEQM-QM9
• GEOM-Drugs

基线

CVGAE，GRAPHDG和CGCF等六种最新的模型作为基线。

结果

构象生成任务

为了测试不同模型所生成构象的质量和多样性。作者评估了建立在两原子坐标矩阵的Frobenius范数基础上的四项指标。

结果显示，GEODIFF在所有的数据集和所有的指标上都比其他的模型表现的要好。

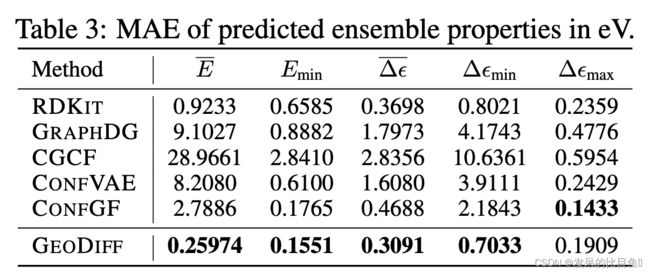
作者使用force field（FF）对结构进行优化，并与同样使用FF进行优化的RDKIT模型进行比较，结果如表3所示。
结果表明GEODIFF+FF有着优越的多样性（Recall metrics）同时显著地提高了准确率（Precision metrics）。

性质预测任务

结果表明：由于性质对于几何结构非常敏感，GEODIFF能够更准确的预测不同分子的构象。