14_计算机视觉Us CNN_2_LeNet-5_ResNet-50_ran out of data_Augmentation_skip_countplot_shape_crop_and_resize

14_Deep Computer Vision Using Convolutional Neural Networks_pool_GridSpec:
https://blog.csdn.net/Linli522362242/article/details/108302266

CNN Architectures

Available models: https://keras.io/api/applications/

LeNet-5

     The LeNet-5 architecture(Yann LeCun et al., “Gradient-Based Learning Applied to Document Recognition,” Proceedings of the IEEE 86, no. 11 (1998): 2278–2324.) is perhaps the most widely known CNN architecture. As mentioned earlier, it was created by Yann LeCun in 1998 and has been widely used for handwritten digit recognition (MNIST). It is composed of the layers shown in Table 14-1.

Table 14-1. LeNet-5 architecture

There are a few extra details to be noted:

• MNIST images are 28 × 28 pixels, but they are zero-padded to 32 × 32 pixels and normalized before being fed to the network. The rest of the network does not use any padding, which is why the size keeps shrinking as the image progresses through the network.
  (MNIST images are 28 × 28 pixels ==> normalization ==> c1 with padding='same')
   
• The average pooling layers are slightly more complex than usual: each neuron computes the mean of its inputs, then multiplies the result by a learnable coefficient (one per map) and adds a learnable bias term (again, one per map), then finally applies the activation function.
   
• Most neurons in C3 maps are connected to neurons in only three or four S2 maps (instead of all six S2 maps). See table 1 (page 8) in the original paper10 for details.
   
• The output layer is a bit special: instead of computing the matrix multiplication of the inputs and the weight vector, each neuron outputs the square of the Euclidian distance between its input vector and its weight vector. Each output measures cost function is now preferred, as it penalizes bad predictions much more, producing larger gradients and converging faster.

Yann LeCun’s website features great demos of LeNet-5 classifying digits.

from tensorflow import keras

(X_train_full, y_train_full), (X_test, y_test) = keras.datasets.mnist.load_data()

import seaborn as sns
import matplotlib.pyplot as plt

fig, ax = plt.subplots(figsize=(8,8))
sns.countplot(y_train_full)

ax.set_title('Distribution of Digits', fontsize=14)
ax.set_xlabel('Digits', fontsize=12)
ax.set_ylabel("count", fontsize=14)
plt.show()

from sklearn.model_selection import train_test_split

X_train, X_valid, y_train, y_valid = train_test_split(X_train_full, y_train_full,
                                                      test_size=0.2, stratify=y_train_full,
                                                      shuffle=True, random_state=42)
# OR
# X_train, X_valid = X_train_full[:-12000], X_train_full[-12000:]
# y_train, y_valid = y_train_full[:-12000], y_train_full[-12000:]

# X_train.shape # (48000, 28, 28)
# X_valid.shape # (12000, 28, 28)

# # normalization
X_train = X_train /255.0
X_valid = X_valid /255.0
X_test = X_test /255.0
X_test.shape

 

def plot_digits(X,y):
    for i in range(20):
        plt.subplot(5, 4, i+1)
        
        plt.tight_layout()
        plt.imshow(X[i], cmap='gray') # since X[i].shape : (28,28) # X[i].reshape(28,28)
        plt.title('Digit:{}'.format(y[i]))
        plt.axis("off")
        
plot_digits(X_train, y_train)

Expand Dimensions

import numpy as np

X_train = X_train[..., np.newaxis] # ==>( batch_size, height, width, channels )
# X_train.shape # (55000, 28, 28, 1)
X_valid = X_valid[..., np.newaxis]
X_test = X_test[..., np.newaxis]
print(X_test.shape)

• Input: 
   
• Conv_1:[] ==> filters=32 feature maps,
                                                         ==>input n=28, Assuming padding='same' then P=2, stride s=1,
                 output shape=(28+2*2-5)/1+1=28 OR since padding='same', Input shape == output shape
                 MNIST images are 28 × 28 pixels, but they are zero-padded to 32 × 32 pixels : 28+2*2
• Pooling_1:[] and pool_size=(2,2) ==> strides=(2,2), padding='valid' and p=0, 
                 output shape=(28+2*0-2)/2+1=14 and filters=32 feature maps,
  
   
• Conv_2:[10x10x48] ==> filters=48 feature maps,
                                                       ==> input n=14, Assuming padding='valid' then P=0, stride s=2,
                 output_shape: ((N+2P-F)/S)+1 = (14+2*0 -5)/1 +1 = 10 x 10
• Pooling_2:[5x5x48] and pool_size=(2,2) ==> strides=(2,2), padding='valid' and p=0, 
                 output shape=(10+2*0-2)/2+1=5 and filters=48 feature maps,
  
   
• FC_1:[256]
• FC_2 and softmax layer:[10]

model = keras.models.Sequential([
    # In + C1
    keras.layers.Conv2D(filters=32, #channels   
                        kernel_size=(5,5),   #==>Filter (F) = 5 x 5
                        strides=(1,1),       #==>strides (S) = 1  
                        padding='same',      #==>input_shape==output_shape ==>P=2
                        data_format='channels_last', #default
                        activation='relu', 
                        input_shape=(28,28,1), #==> Parameters: Input (N) = 28
                        name='Conv_1',
                       ),# Output_shape: ((N+2P-F)/S)+1 = ((28+4-5)/1)+1 = 28x28
    # We will apply 32 filters / kernels so we will get a [batches x 28 x 28 x 32] dimensional output
    # model2.compute_output_shape(input_shape=(None, 28,28,1))
    # TensorShape([None, 28, 28, 32])
    
    # S2                                     #Input (N) = 28
    keras.layers.AvgPool2D(#pool_size=(2,2),  #default ==> F=2
                           strides=(2,2),     #==>strides (S) = 2 #If None, it will default to pool_size.
                           padding='valid',   #==>padding(p):0
                          ),# Output_shape: ((N+2P-F)/S)+1 = ((28-2)/2)+1 = 14x14
    #TensorShape([None, 14, 14, 32])
    
    # C3                                    #Input (N) = 14
    keras.layers.Conv2D(filters=48,  #feature maps
                        kernel_size=(5,5),  #==>Filter (F) = 5 x 5 
                        strides=(1,1),      #==>strides (S) = 1
                        padding='valid',    #==>padding(p):0 
                        activation='relu',
                        name='Conv_3',
                       ),# Output_shape: ((N+2P-F)/S)+1 = ((14-5)/1)+1 = 10 x 10
    #TensorShape([None, 10, 10, 48])
    
    # S4
    keras.layers.AvgPool2D(#pool_size=(2,2),  #default ==> F=2
                           strides=(2,2),     #==>strides (S) = 2 #If None, it will default to pool_size.
                           padding='valid',   #==>padding(p):0
                          ),# Output_shape:((N+2P-F)/S)+1 = ((10-2)/2)+1 = 5 x 5
    #TensorShape([None, 5, 5, 48])
    
    # C5
    keras.layers.Flatten(), #==> 2D (None, 1200=5*5*48)
    keras.layers.Dense(units=256, activation='relu'),
    # F6
    keras.layers.Dense(units=84, activation='relu'),
    # out
    keras.layers.Dense(units=10, activation = 'softmax'),
])

model.build()
model.summary()

Flatten : since a dense network expects a 1D array of features for each instance 

model.compute_output_shape( input_shape=(None, 28,28,1) )

 

from keras.optimizers import Adam

adam = Adam(lr=5e-4)
model.compile( loss="sparse_categorical_crossentropy", 
               optimizer=adam, 
               metrics=["accuracy"])

history = model.fit(X_train, y_train, epochs=10, validation_data=(X_valid, y_valid))
score = model.evaluate(X_test, y_test)

print(score)

https://www.kaggle.com/curiousprogrammer/lenet-5-cnn-with-keras-99-48
http://yann.lecun.com/exdb/lenet/

AlexNet

     The AlexNet CNN architecture(Alex Krizhevsky et al., “ImageNet Classification with Deep Convolutional Neural Networks,” _Proceedings of the 25th International Conference on Neural Information Processing Systems 1 (2012): 1097–1105.) won the 2012 ImageNet ILSVRC challenge by a large margin: it achieved a top-five error rate of 17%, while the second best achieved only 26%! It was developed by Alex Krizhevsky (hence the name), Ilya Sutskever, and Geoffrey Hinton. It is similar to LeNet-5, only much larger and deeper, and it was the first to stack convolutional layers directly on top of one another, instead of stacking a pooling layer on top of each convolutional layer. Table 14-2 presents this architecture.

Table 14-2. AlexNet architecture

http://www.cs.toronto.edu/~hinton/absps/imagenet.pdf

     To reduce overfitting, the authors used two regularization techniques. First, they applied dropout (introduced in Chapter 11) with a 50% dropout rate during training to the outputs of layers F9 and F10. Second, they performed data augmentation数据增强 by randomly shifting the training images by various offsets, flipping them horizontally, and changing the lighting conditions.
##########################################################

Data Augmentation: https://blog.csdn.net/Linli522362242/article/details/108414534

     Data augmentation artificially increases the size of the training set by generating many realistic variants of each training instance. This reduces overfitting, making this a regularization technique. The generated instances should be as realistic as possible: ideally, given an image from the augmented training set, a human should not be able to tell whether it was augmented or not. Simply adding white noise will not help; the modifications should be learnable (white noise is not).

Figure 14-12. Generating new training instances from existing ones

     For example, you can slightly shift, rotate, and resize every picture in the training set by various amounts and add the resulting pictures to the training set (see Figure 14-12). This forces the model to be more tolerant to variations in the position, orientation, and size of the objects in the pictures. For a model that’s more tolerant of different lighting conditions, you can similarly generate many images with various contrasts. In general, you can also flip the pictures horizontally (except for text, and other asymmetrical objects). By combining these transformations, you can greatly increase the size of your training set.
##########################################################

     AlexNet also uses a competitive normalization step immediately after the ReLU step of layers C1 and C3, called local response normalization (LRN): the most strongly activated neurons inhibit抑制 other neurons located at the same position in neighboring feature maps (such competitive activation has been observed in biological neurons). This encourages different feature maps to specialize, pushing them apart and forcing them to explore a wider range of features, ultimately improving generalization. Equation 14-2 shows how to apply LRN.

Equation 14-2. Local response normalization (LRN)

In this equation:

• is the normalized output of the neuron located in feature map i, at some row u and column v (note that in this equation we consider only neurons located at this row and column, so u and v are not shown).
• is the activation of that neuron after the ReLU step, but before normalization.
• k, α, β, and r are hyperparameters. k is called the bias, and r is called the depth radius(OR r “adjacent” kernel maps at the same spatial position).
• is the number of feature maps.

     For example, if r = 2 and a neuron has a strong activation, it will inhibit the activation of the neurons located in the feature maps immediately above( i+2/2=i+1) and below( i-2/2=i-1 ) its own.

     In AlexNet, the hyperparameters are set as follows: r = 2, α = 0.00002, β = 0.75, and k = 1. This step can be implemented using the tf.nn.local_response_normalization() function (which you can wrap in a Lambda layer if you want to use it in a Keras model).

     A variant of AlexNet called ZF Net(Matthew D. Zeiler and Rob Fergus, “Visualizing and Understanding Convolutional Networks,” Proceedings of the European Conference on Computer Vision (2014): 818-833.) was developed by Matthew Zeiler and Rob Fergus and won the 2013 ILSVRC challenge. It is essentially AlexNet with a few tweaked hyperparameters (number of feature maps, kernel size, stride, etc.).

     This scheme bears some resemblance to the local contrast normalization scheme of Jarrett et al., but ours would be more correctly termed “brightness normalization”, since we do not subtract the mean activity. Response normalization reduces our top-1 and top-5 error rates by 1.4% and 1.2%, respectively. We also verified the effectiveness of this scheme on the CIFAR-10 dataset: a four-layer CNN achieved a 13% test error rate without normalization and 11% with normalization.

     AlexNet中每个池化层之后都有局部响应归一化层。归一化层的目的是避免随着层级的加深而导致的信息出现逐层递减的趋势，起到加快神经网络收敛速度的作用。但是，近些年来的研究表明，局部响应归一化层对神经网络的训练过程起到的帮助很小，所以就渐渐不再被使用了。

GoogLeNet

     The GoogLeNet architecture was developed by Christian Szegedy et al. from Google Research,13 and it won the ILSVRC 2014 challenge by pushing the top-five error rate below 7%. This great performance came in large part from the fact that the network was much deeper than previous CNNs (as you’ll see in Figure 14-14). This was made possible by subnetworks called inception modules启动模块, 初始模块,(In the 2010 movie Inception, the characters keep going deeper and deeper into multiple layers of dreams; hence the name of these modules.) which allow GoogLeNet to use parameters much more efficiently than previous architectures: GoogLeNet actually has 10 times fewer parameters than AlexNet (roughly 6 million instead of 60 million).
 Figure 14-13. Inception module
VS

     Figure 14-13 shows the architecture of an inception module. The notation “3 × 3 + 1(S)” means that the layer uses a 3 × 3 kernel, stride 1, and "same" padding. The input signal is first copied and fed to four different layers. All convolutional layers use the ReLU activation function. Note that the second set of convolutional layers uses different kernel sizes (1 × 1, 3 × 3, and 5 × 5), allowing them to capture patterns at different scales. Also note that every single layer uses a stride of 1 and "same" padding (even the max pooling layer), so their outputs all have the same height and width as their inputs. This makes it possible to concatenate all the outputs along the depth dimension(###along channels orientation###) in the final depth concatenation layer (i.e., stack the feature maps from all four top convolutional layers). This concatenation layer can be implemented in Tensor‐Flow using the tf.concat() operation, with axis=3 (the axis is the depth).

from keras.layers import Input
input_img = Input(shape = (32, 32, 3))

from keras.layers import Conv2D, MaxPooling2D

#  # function API # default strides=(1, 1)
tower_1 = Conv2D(64, (1,1), padding='same', activation='relu')(input_img)
tower_1 = Conv2D(64, (3,3), padding='same', activation='relu')(tower_1)

tower_2 = Conv2D(64, (1,1), padding='same', activation='relu')(input_img)
tower_2 = Conv2D(64, (5,5), padding='same', activation='relu')(tower_2)

tower_3 = MaxPooling2D((3,3), strides=(1,1), padding='same')(input_img)
tower_3 = Conv2D(64, (1,1), padding='same', activation='relu')(tower_3)

output = keras.layers.concatenate([tower_1, tower_2, tower_3], axis = 3) # axis=0 is num_batches, axis=3 is the depth

https://becominghuman.ai/understanding-and-coding-inception-module-in-keras-eb56e9056b4b

      We learn 64 1x1 filters on the input_img tensor and then we learn 64 3x3 filters on the tower_1 tensor. Similarly, we make tower_2, tower_3 tensors.

      Note: We provide input_img tensor to tower_2 and tower_3 as input so all the 3x3, 5x5 filters and the max pooling layers are performed on the same input.

      The padding is kept same so that the output shape of the Conv2D operation is same as the input shape. So, the final output of each filter of tower_1, tower_2 and tower_3 is same. Thus we can easily concatenate these filters to form the output of our inception module.

#####################################################

图14-13可以看到对输入做了4个分支，分别用不同尺寸的filter进行卷积或池化，最后再在特征维度上拼接到一起。这种全新的结构有什么好处呢？Szegedy从多个角度进行了解释：

解释1：在直观感觉上在多个尺度上同时进行卷积，能提取到不同尺度的特征。特征更为丰富也意味着最后分类判断时更加准确。

解释2：利用稀疏矩阵分解成密集矩阵计算的原理来加快收敛速度。举个例子下图左侧是个稀疏矩阵（很多元素都为0，不均匀分布在矩阵中），和一个2x2的矩阵进行卷积，需要对稀疏矩阵中的每一个元素进行计算；如果像右图那样把稀疏矩阵分解成2个子密集矩阵，再和2x2矩阵进行卷积，稀疏矩阵中0较多的区域就可以不用计算，计算量就大大降低。这个原理应用到inception上就是要在特征维度上进行分解！传统的卷积层的输入数据只和一种尺度（比如3x3）的卷积核进行卷积，输出固定维度（比如256个特征）的数据，所有256个输出特征基本上是均匀分布在3x3尺度范围上，这可以理解成输出了一个稀疏分布的特征集；而inception模块在多个尺度上提取特征（比如1x1，3x3，5x5），输出的256(=96+96+64)个特征就不再是均匀分布，而是相关性强的特征聚集在一起（比如1x1的的96个特征聚集在一起，3x3的96个特征聚集在一起，5x5的64个特征聚集在一起），这可以理解成多个密集分布的子特征集。这样的特征集中因为相关性较强的特征聚集在了一起，不相关的非关键特征就被弱化，同样是输出256个特征，inception方法输出的特征“冗余”的信息较少。用这样的“纯”的特征集层层传递最后作为反向计算的输入，自然收敛的速度更快。

图4: 将稀疏矩阵分解成子密集矩阵来进行计算

解释3：Hebbin赫布原理。Hebbin原理是神经科学上的一个理论，解释了在学习的过程中脑中的神经元所发生的变化，用一句话概括就是fire togethter, wire together。赫布认为“两个神经元或者神经元系统，如果总是同时兴奋，就会形成一种‘组合’，其中一个神经元的兴奋会促进另一个的兴奋”。比如狗看到肉会流口水，反复刺激后，脑中识别肉的神经元会和掌管唾液分泌的神经元会相互促进，“缠绕”在一起，以后再看到肉就会更快流出口水。用在inception结构中就是要把相关性强的特征汇聚到一起。这有点类似上面的解释2，把1x1，3x3，5x5的特征分开。因为训练收敛的最终目的就是要提取出独立的特征，所以预先把相关性强的特征汇聚，就能起到加速收敛的作用。

在inception模块中有一个分支使用了max pooling，Other than reducing computations, memory usage, and the number of parameters, a max pooling layer(Only the max input value in each receptive field makes it to the next layer, while the other inputs are dropped) also introduces some level of invariance不变性 to small translations,。
https://www.cnblogs.com/leebxo/p/10315490.html
#####################################################

     You may wonder why inception modules have convolutional layers with 1 × 1 kernels. Surely these layers cannot capture any features because they look at only one pixel at a time? In fact, the layers serve three purposes:

• Although they cannot capture spatial patterns, they can capture patterns along the depth dimension. e.g. # along the depth dimension ( k_size=(1, 1, 1, 3) and strides=(1, 1, 1, 3) : kernel size=(1,1) stride size=(1,1) ) with a divisor of the input depth=3 https://blog.csdn.net/Linli522362242/article/details/108302266

  output = tf.nn.max_pool(images,
                          ksize=(1, 1, 1, 3),
                          strides=(1, 1, 1, 3),
                          padding="same")

They are configured to output fewer feature maps than their inputs, so they serve as bottleneck layers, meaning they reduce dimensionality. This cuts the computational cost and the number of parameters, speeding up training and improving generalization.
##########################################


使用1x1卷积(W*X, element-wise multiplication)进行降维，降低了计算复杂度。图2中间3x3卷积和5x5卷积前的1x1卷积都起到了这个作用。当某个卷积层输入的特征数较多，对这个输入进行卷积运算将产生巨大的计算量；如果对输入先进行降维，减少特征数后再做卷积计算量就会显著减少。下图是优化前后两种方案的乘法次数比较，同样是输入一组有192个特征feature maps、32x32大小，输出256组特征的数据，
     第一张图直接用3x3卷积实现，需要1x 3x3x192x256 x 32x32=452984832次乘法；(3x3x192x256 is the kernel matrix W)
     第二张图先用1x1的卷积降到96个特征(the number of output feature maps)，再用3x3卷积恢复出256组特征，需要1x1x192x96 x 32x32 + 3x3x96x256 x 32x32=245366784次乘法，使用1x1卷积降维的方法节省了一半的计算量。有人会问，用1x1卷积降到96个特征后特征数不就减少了么，会影响最后训练的效果么？答案是否定的，只要最后输出的特征数不变（256组），中间的降维类似于压缩的效果，并不影响最终训练的结果???。

##########################################

• Each pair of convolutional layers ([1 × 1, 3 × 3] and [1 × 1, 5 × 5]) acts like a single powerful convolutional layer, capable of capturing more complex patterns. Indeed, instead of sweeping a simple linear classifier across the image (as a single convolutional layer does), this pair of convolutional layers sweeps a two-layer neural network across the image.
  ##########################################
  https://arxiv.org/pdf/1312.4400.pdf
  
  左侧是是传统的卷积层结构（线性卷积f linear convolution layer），在一个尺度上只有一次卷积；
  右图是Network in Network结构（NIN结构），先进行一次普通的卷积（比如3x3），紧跟再进行一次1x1的卷积，对于某个像素点来说1x1卷积等效于该像素点在所有特征上进行一次全连接的计算，所以右侧图的1x1卷积画成了全连接层的形式，需要注意的是NIN结构中无论是第一个3x3卷积还是新增的1x1卷积，后面都紧跟着激活函数（比如relu）。将两个卷积串联，就能组合出更多的非线性特征。举个例子，假设第1个3x3卷积＋激活函数近似于f1(x)=ax2+bx+c，第二个1x1卷积＋激活函数近似于f2(x)=mx2+nx+q，那f1(x)和f2(f1(x))比哪个非线性更强，更能模拟非线性的特征？答案是显而易见的。NIN的结构和传统的神经网络中多层的结构有些类似，后者的多层是跨越了不同尺寸的感受野（通过层与层中间加pool层），从而在更高尺度上提取出特征；NIN结构是在同一个尺度上的多层（中间没有pool层），从而在相同的感受野范围能提取更强的非线性。
  ##########################################

     In short, you can think of the whole inception module as a convolutional layer on steroids, able to output feature maps that capture complex patterns at various scales.

     The number of convolutional kernels for each convolutional layer is a hyperparameter. Unfortunately, this means that you have six more hyperparameters to tweak for every inception layer you add.

     Now let’s look at the architecture of the GoogLeNet CNN (see Figure 14-14). The number of feature maps output by each convolutional layer and each pooling layer is shown before the kernel size. The architecture is so deep that it has to be represented in three columns, but GoogLeNet is actually one tall stack, including nine inception modules (the boxes with the spinning tops). The six numbers in the inception modules represent the number of feature maps output by each convolutional layer in the module (in the same order as in Figure 14-13). Note that all the convolutional layers use the ReLU activation function.
Figure 14-14. GoogLeNet architecture

Let’s go through this network:

• The first two layers ###Convolution(stride=2, padding='valid') + Max pool(stride=2, padding='valid')### divide the image’s height and width by 4 (so its area is divided by 16), to reduce the computational load. The first layer uses a large kernel size(7x7) so that much of the information is preserved.
   
• Then the local response normalization layer ensures that the previous layers learn a wide variety of features ###(local response normalization (LRN) : the most strongly activated neurons inhibit抑制 other neurons located at the same position in neighboring feature maps. This encourages different feature maps to specialize, pushing them apart and forcing them to explore a wider range of features, ultimately improving generalization)###.
   
• Two convolutional layers follow, where the first acts like a bottleneck layer. As explained earlier, you can think of this pair as a single smarter convolutional layer.###Each pair of convolutional layers ([1 × 1, 3 × 3] and [1 × 1, 5 × 5]) acts like a single powerful convolutional layer, capable of capturing more complex patterns. Indeed, instead of sweeping a simple linear classifier across the image (as a single convolutional layer does), this pair of convolutional layers sweeps a two-layer neural network across the image.###
   
• Again, a local response normalization layer ensures that the previous layers capture a wide variety of patterns.
   
• Next, a max pooling layer reduces the image height and width by 2 ###Convolution(stride=2, padding='valid')###, again to speed up computations.
• Then comes the tall stack of nine inception modules, interleaved with a couple max pooling layers to reduce dimensionality and speed up the net.
   

• Next, the global average pooling layer https://blog.csdn.net/Linli522362242/article/details/108414534 outputs the mean of each feature map: this drops any remaining spatial information(widthxheight), which is fine because there was not much spatial information left at that point. Indeed, GoogLeNet input images are typically expected to be 224 × 224 pixels, so after 5 max pooling layers, each dividing the height and width by 2, the feature maps are down to 7 × 7. Moreover, it is a classification task, not localization, so it does not matter where the object is. Thanks to the dimensionality reduction brought by this layer, there is no need to have several fully connected layers at the top of the CNN (like in AlexNet), and this considerably reduces the number of parameters in the network and limits the risk of overfitting.

• The last layers are self-explanatory: dropout for regularization, then a fully connected layer with 1,000 units (since there are 1,000 classes) and a softmax activation functionhttps://blog.csdn.net/Linli522362242/article/details/104124771 to output estimated class probabilities.

     This diagram is slightly simplified: the original GoogLeNet architecture also included two auxiliary[ɔːɡˈzɪliəri]辅助 classifiers plugged on top of the third and sixth inception modules. They were both composed of one average pooling layer, one convolutional layer, two fully connected layers, and a softmax activation layer. During training, their loss (scaled down by 70%) was added to the overall loss. The goal was to fight the vanishing消失了 gradients problem and regularize the network. However, it was later shown that their effect was relatively minor.

     Several variants of the GoogLeNet architecture were later proposed by Google researchers, including Inception-v3 and Inception-v4, using slightly different inception modules and reaching even better performance.

VGGNet

     The runner-up in the ILSVRC 2014 challenge was VGGNet,15 developed by Karen Simonyan and Andrew Zisserman from the Visual Geometry Group (VGG) research lab at Oxford University. It had a very simple and classical architecture, with 2 or 3 convolutional layers and a pooling layer, then again 2 or 3 convolutional layers and a pooling layer, and so on (reaching a total of just 16 or 19 convolutional layers, depending on the VGG variant), plus a final dense network with 2 hidden layers and the output layer. It used only 3 × 3 filters, but many filters.

ResNet

What problems ResNets solve?

     One of the problems ResNets solve is the famous known vanishing消失 gradient. This is because when the network is too deep, the gradients(e.g. https://blog.csdn.net/Linli522362242/article/details/96480059)
from where the loss function(e.g.
) is calculated easily shrink to zero after several applications of the chain rule. This result on the weights never updating its values and therefore, no learning is being performed.

     With ResNets, the gradients can flow directly through the skip connections backwards from later layers to initial filters(called kernel weights).

     Kaiming He et al. won the ILSVRC 2015 challenge using a Residual Network (or ResNet), ###Kaiming He et al., “Deep Residual Learning for Image Recognition,” arXiv preprint arXiv:1512:03385 (2015)### that delivered an astounding惊人 top-five error rate under 3.6%. The winning variant used an extremely deep CNN composed of 152 layers (other variants had 34, 50, and 101 layers). It confirmed the general trend: models are getting deeper and deeper, with fewer and fewer parameters. The key to being able to train such a deep network is to use skip connections (also called shortcut connections): the signal feeding into a layer is also added to the output of a layer located a bit higher up the stack. Let’s see why this is useful.

     When training a neural network, the goal is to make it model a target function h(x). If you add the input x to the output of the network (i.e., you add a skip connection), then the network will be forced to model f(x) = h(x) – x rather than h(x). This is called residual learning (see Figure 14-15).
Figure 14-15. Residual learning

Figure 10-14. Wide & Deep neural network: 
10_Introduction to Artificial Neural_4_Regression MLP_Sequential_Subclassing_saveMode_Callback_board: 
https://blog.csdn.net/Linli522362242/article/details/106582512
https://blog.csdn.net/Linli522362242/article/details/107459161

     When you initialize a regular neural network, its weights are close to zero, so the network just outputs values close to zero( f(x)~~>0 ). If you add a skip connection, the resulting network just outputs a copy of its inputs; in other words, it initially models the identity function x. If the target function h(x) is fairly close to the identity function x (which is often the case, The intuition is that residual learning f(x)=0 has to be easy for the network ), this will speed up training considerably.

     Moreover, if you add many skip connections, the network can start making progress even if several layers have not started learning yet (see Figure 14-16). Thanks to skip connections, the signal can easily make its way across the whole network. The deep residual network can be seen as a stack of residual units (RUs), where each residual unit is a small neural network with a skip connection.
Figure 14-16. Regular deep neural network (left) and deep residual network (right)

     Now let’s look at ResNet’s architecture (see Figure 14-17). It is surprisingly simple. It starts and ends exactly like GoogLeNet (except without a dropout layer), and in between is just a very deep stack of simple residual units. Each residual unit is composed of two convolutional layers (and no pooling layer!), with Batch Normalization (BN) and ReLU activation, using 3 × 3 kernels and preserving spatial dimensions (stride 1, "same" padding).
Figure 14-17. ResNet architecture

      Note that the number of feature maps is doubled every few residual units(from 64 to 128), at the same time as their height and width are halved (using a convolutional layer with stride 2). When this happens, the inputs cannot be added directly to the outputs of the residual unit because they don’t have the same shape (for example, this problem affects the skip connection represented by the dashed arrow in Figure 14-17). To solve this problem, the inputs are passed through a 1 × 1 convolutional layer with stride 2 and the right number of output feature maps (see Figure 14-18).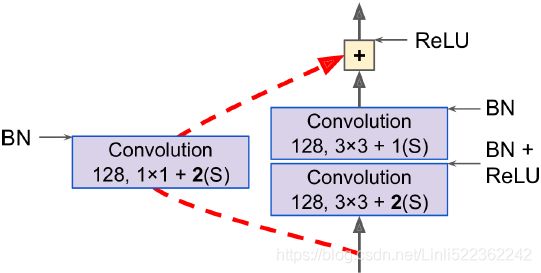
Figure 14-18. Skip connection when changing feature map size(stride 2) and depth (from 64 to 128)

     ResNet-34 is the ResNet with 34 layers (only counting the convolutional layers and the fully connected layer) ###It is a common practice when describing a neural network to count only layers with parameters.### containing 3 residual units that output 64 feature maps, 4 RUs with 128 maps, 6 RUs with 256 maps, and 3 RUs with 512 maps. We will implement this architecture later in this chapter.

Implementing a ResNet-34 CNN Using Keras

     Most CNN architectures described so far are fairly straightforward to implement (although generally you would load a pretrained network instead, as we will see). To illustrate the process, let’s implement a ResNet-34 from scratch using Keras. First, let’s create a ResidualUnit layer:

from functools import partial
from tensorflow import keras

DefaultConv2D = partial( keras.layers.Conv2D, kernel_size = 3, strides=1, padding='SAME', use_bias=False )

<==

class ResidualUnit( keras.layers.Layer):
  def __init__(self, filters, strides=1, activation='relu', **kwargs):
    super().__init__(**kwargs)
    self.activation = keras.activations.get( activation )
    ###################
    self.main_layers = [ DefaultConv2D(filters, strides=strides), # default kernel_size = 3, padding='SAME'
                         keras.layers.BatchNormalization(),
                         self.activation,
                         
                         DefaultConv2D(filters),       # default kernel_size = 3, strides=1, padding='SAME'
                         keras.layers.BatchNormalization(),
                       ]
    ###################
    self.skip_layers=[]
    if strides>1 : # here, strides==2
      self.skip_layers = [
                           DefaultConv2D( filters, kernel_size=1, strides=2),
                           keras.layers.BatchNormalization()
                         ]

  def call(self, inputs):
    Z = inputs
    for layer in self.main_layers:
      Z = layer(Z)

    skip_Z=inputs
    for layer in self.skip_layers:
      skip_Z = layer( skip_Z )

    return self.activation( Z+skip_Z )

     As you can see, this code matches Figure 14-18 pretty closely. In the constructor, we create all the layers we will need: the main layers are the ones on the right side of the diagram, and the skip layers are the ones on the left (only needed if the stride is greater than 1). Then in the call() method, we make the inputs go through the main layers and the skip layers (if any), then we add both outputs and apply the activation function. 

   Convolution ==> Max Pooling  https://towardsdatascience.com/understanding-and-visualizing-resnets-442284831be8

     Next, we can build the ResNet-34 using a Sequential model, since it’s really just a long sequence of layers (we can treat each residual unit as a single layer now that we have the ResidualUnit class):
# GoogLeNet input images are typically expected to be 224 × 224 pixels, use_bias=False

     ResNet-34 is the ResNet with 34 layers (only counting the convolutional layers and the fully connected layer, 34=1+3*2+4*2+6*2+3*2+1) ###It is a common practice when describing a neural network to count only layers with parameters.### containing 3 residual units that output 64 feature maps, 4 RUs with 128 maps, 6 RUs with 256 maps, and 3 RUs with 512 maps

model = keras.models.Sequential([
    # GoogLeNet input images are typically expected to be 224 × 224 pixels, use_bias=False
    DefaultConv2D( 64, kernel_size=7, strides=2, input_shape=[224,224,3] ), # a convolutional layer
    # padding='SAME' and strides=2 ==> output_shape = input_shape/2 = 224/112
    # TensorShape([None, 112, 112, 64]) # ((N+2P-F)/S)+1 = ((224+2*P-7)/2)+1=112 ==>P=3

    keras.layers.BatchNormalization(),  ######
    keras.layers.Activation('relu'),    ######


    keras.layers.MaxPool2D(pool_size=3, strides=2, padding='SAME'), 
    # padding='SAME' and strides=2 ==> output_shape=input_shape/2 =112/2=56
    # TensorShape([None, 56, 56, 64])   # ((N+2P-F)/S)+1 = ((112+2*1-3)/2)+1 =56
])

# 3 residual units that output 64 feature maps, 4 Residual Units with 128 maps, 
# 6 RUs with 256 maps, and 3 RUs with 512 maps
prev_filters = 64 # filter maps
for filters in [64]*3 + [128]*4 + [256]*6 + [512]*3 :
  strides = 1 if filters == prev_filters else 2
  # Skip connection when changing feature map size and depth ==> strides=2
  model.add( ResidualUnit(filters, strides=strides) )
  prev_filters = filters

model.add( keras.layers.GlobalAvgPool2D() )
model.add( keras.layers.Flatten() ) # since a dense network expects a 1D array of features for each instance
model.add( keras.layers.Dense( 10, activation='softmax' ) )#TensorShape([None, 10]) # a fully connected layer

#model.compute_output_shape( input_shape=[None,224,224,3] ) 
model.summary()

     The only slightly tricky part in this code is the loop that adds the ResidualUnit layers to the model: as explained earlier, the first 3 RUs have 64 filters, then the next 4 RUs have 128 filters, and so on. We then set the stride to 1 when the number of filters is the same as in the previous RU, or else we set it to 2. Then we add the ResidualUnit, and finally we update prev_filters. 

     It is amazing that in fewer than 40 lines of code, we can build the model that won the ILSVRC 2015 challenge! This demonstrates both the elegance of the ResNet model and the expressiveness of the Keras API. Implementing the other CNN architectures is not much harder. However, Keras comes with several of these architectures built in, so why not use them instead?

 Trainable parameters: 7*7*3*64 +0 (since use_bias=False) =9408

 

Using Pretrained Models from Keras ( ResNet50)

     In general, you won’t have to implement standard models like GoogLeNet or ResNet manually, since pretrained networks are readily available with a single line of code in the keras.applications package. For example, you can load the ResNet-50 model, pretrained on ImageNet, with the following line of code:

# create a ResNet-50 model and download weights pretrained on the ImageNet dataset.
model = keras.applications.resnet50.ResNet50(weights="imagenet")
model.summary()

 

     That’s all! This will create a ResNet-50 model and download weights pretrained on the ImageNet dataset. To use it, you first need to ensure that the images have the right size. A ResNet-50 model expects 224 × 224-pixel images (other models may expect other sizes, such as 299 × 299), so let’s use TensorFlow’s tf.image.resize() function to resize the images we loaded earlier:

import numpy as np
from sklearn.datasets import load_sample_image
import matplotlib.pyplot as plt
 
# scale these features simply by dividing by 255, to get floats ranging from 0 to 1.
china = load_sample_image("china.jpg") / 255   # china.shape: (427, 640, 3)
flower = load_sample_image("flower.jpg") / 255 # flower.shape: (427, 640, 3)
images = np.array([china, flower])  # images.shape: (2, 427, 640, 3)

def plot_color_image(image):
    plt.imshow(image, interpolation="nearest")
    plt.axis("off")

images_resized = tf.image.resize( images, [224,224]) # (2, 224,224,3 )
plot_color_image( images_resized[0] )
plt.show()

 
# china.shape: (427, 640, 3) # tower
# flower.shape: (427, 640, 3)

# Resizes an image to a target width and height by either centrally cropping 
# the image or padding it evenly with zeros.

# If width or height is greater than the specified target_width or target_height 
# respectively, this op centrally crops along that dimension. If width or height 
# is smaller than the specified target_width or target_height respectively, this
# op centrally pads with 0 along that dimension.
images_resized = tf.image.resize_with_crop_or_pad( images, 224, 224)
plot_color_image( images_resized[0] )
plt.show()

     The tf.image.resize() will not preserve the aspect ratio长宽比. If this is a problem, try cropping the images to the appropriate aspect ratio before resizing. Both operations can be done in one shot with tf.image.crop_and_resize().

###########################
image : A 4-D tensor of shape [batch, image_height, image_width, depth]. Both image_height and image_width need to be positive.
boxes : A 2-D tensor of shape [num_boxes, 4]. The i-th row of the tensor specifies the coordinates of a box in the box_ind[i] image and is specified in normalized coordinates [y1, x1, y2, x2]. A normalized coordinate value of y is mapped to the image coordinate at y * (image_height - 1), so as the [0, 1] interval of normalized image height is mapped to [0, image_height - 1] in image height coordinates. We do allow y1 > y2, in which case the sampled crop is an up-down flipped version of the original image. The width dimension is treated similarly. Normalized coordinates outside the [0, 1] range are allowed, in which case we use extrapolation_value to extrapolate the input image values.
(e.g. image_height=427 , image_width=640 and pixels after normalization( /255.0) then ==> china_box = [0, 0.03, 1, 0.68] percentages==>actual [ 0*427=0, 0.03*640=19.2, 1*427=427, 0.68*640=435.2 ] ==> resize[224,224]
box_indices : A 1-D tensor of shape [num_boxes] with int32 values in [0,batch). The value of box_ind[i] specifies the image that the i-th box refers to.
################################################## axes: vertical-y and horizontal -x

china_box = [0, 0.03, 1, 0.68] # crop range(positions) in percentages
flower_box = [0.19, 0.26, 0.86, 0.7]
images_resized = tf.image.crop_and_resize( images, 
                                          boxes=[china_box, flower_box], box_indices=[0,1], 
                                          crop_size=[224,224])
plot_color_image( images_resized[0] )
plt.show()

plot_color_image( images_resized[1] )
plt.show()

Select the predicted object ： 

 

     The pretrained models assume that the images are preprocessed in a specific way. In some cases they may expect the inputs to be scaled from 0 to 1, or –1 to 1, and so on. Each model provides a preprocess_input() function that you can use to preprocess your images. These functions assume that the pixel values range from 0 to 255(normalization), so we must multiply them by 255 (since earlier we scaled them to the 0–1 range):

inputs = keras.applications.resnet50.preprocess_input( images_resized*255 )# images_resized.shape : TensorShape([2, 224, 224, 3])

# Now we can use the pretrained model to make predictions:
Y_proba = model.predict( inputs )
# Y_proba.shape : (2, 1000)

      As usual, the output Y_proba is a matrix with one row per image and one column per class (in this case, there are 1,000 classes). If you want to display the top K predictions, including the class name and the estimated probability of each predicted class, use the decode_predictions() function. For each image, it returns an array containing the top K predictions, where each prediction is represented as an array containing the class identifier,(In the ImageNet dataset, each image is associated to a word in the WordNet dataset: the class ID is just a WordNet ID.) its name, and the corresponding confidence score:

top_K = keras.applications.resnet50.decode_predictions(Y_proba, top=3)
# Returns: A list of lists of top class prediction tuples 
# (class_name, class_description, score). 
# One list of tuples per sample in batch input.

for image_index in range( len(images) ):
  print( "Image #{}".format(image_index) )

  for class_id, name, y_proba in top_K[image_index]:
    print("   {} - {:12s} {:.2f}%".format( class_id, name, y_proba*100) )
  print()

The output looks like this: 

 

     The correct classes (monastery and daisy) appear in the top three results for both images. That’s pretty good, considering that the model had to choose from among 1,000 classes.

     As you can see, it is very easy to create a pretty good image classifier using a pretrained model. Other vision models are available in keras.applications, including several ResNet variants, GoogLeNet variants like Inception-v3 and Xception, VGGNet variants, and MobileNet and MobileNetV2 (lightweight models for use in mobile applications).

     But what if you want to use an image classifier for classes of images that are not part of ImageNet? In that case, you may still benefit from the pretrained models to perform transfer learning.

     ResNets deeper than that, such as ResNet-152, use slightly different residual units. Instead of two 3 × 3 convolutional layers with, say, 256 feature maps, they use three convolutional layers: first a 1 × 1 convolutional layer with just 64 feature maps (4 times less), which acts as a bottleneck layer (as discussed already), then a 3 × 3 layer with 64 feature maps, and finally another 1 × 1 convolutional layer with 256 feature maps (4 times 64) that restores the original depth. ResNet-152 contains 3 such RUs that output 256 maps, then 8 RUs with 512 maps, a whopping 36 RUs with 1,024 maps, and finally 3 RUs with 2,048 maps.

     Google’s Inception-v418 architecture merged the ideas of GoogLeNet and ResNet and achieved a top-five error rate of close to 3% on ImageNet classification.

Xception

     Another variant of the GoogLeNet architecture is worth noting: Xception19 (which stands for Extreme Inception) was proposed in 2016 by François Chollet (the author of Keras), and it significantly outperformed Inception-v3 on a huge vision task (350 million images and 17,000 classes). Just like Inception-v4, it merges the ideas of GoogLeNet and ResNet, but it replaces the inception modules with a special type of layer called a depthwise separable convolution layer (or separable convolution layer for short ###This name can sometimes be ambiguous, since spatially separable convolutions are often called “separable convolutions” as well.### ). These layers had been used before in some CNN architectures, but they were not as central as in the Xception architecture. While a regular convolutional layer uses filters that try to simultaneously capture spatial patterns (e.g., an oval) and cross channel patterns (e.g., mouth + nose + eyes = face), a separable convolutional layer makes the strong assumption that spatial patterns and cross-channel patterns can be modeled separately (see Figure 14-19). Thus, it is composed of two parts: the first part applies a single spatial filter for each input feature map, then the second part looks exclusively for cross-channel patterns—it is just a regular convolutional layer with 1 × 1 filters.
  Figure 14-19. Depthwise separable convolutional layer ( too few channels, just for illustration purposes) from bottom to up

     Since separable convolutional layers only have one spatial filter per input channel, you should avoid using them after layers(e.g. input layer) that have too few channels避免在通道太少的图层之后使用它们, such as the input layer (granted, that’s what Figure 14-19 represents, but it is just for illustration purposes). For this reason, the Xception architecture starts with 2 regular convolutional layers, but then the rest of the architecture uses only separable convolutions (34 in all), plus a few max pooling layers and the usual final layers (a global average pooling layer and a dense output layer).

##############################################################

1. Original Depthwise Separable Convolution https://towardsdatascience.com/review-xception-with-depthwise-separable-convolution-better-than-inception-v3-image-dc967dd42568

The original depthwise separable convolution is the depthwise convolution followed by a pointwise convolution.

1. Depthwise convolution(spatial-only filters, 1 per input channel) is the channel-wise n×n spatial convolution. Suppose in the figure above, we have 5 channels, then we will have 5 n×n spatial convolution( height x width x 5channels).
2. Pointwise convolution（cross-channel） actually is the 1×1 convolution to change the dimension.

Compared with conventional convolution, we do not need to perform convolution across all channels. That means the number of connections are fewer and the model is lighter.

2. Modified Depthwise Separable Convolution in Xception
The Modified Depthwise Separable Convolution used as an Inception Module in Xception, so called “extreme” version of Inception module (n=3 here)

     The modified depthwise separable convolution is the pointwise convolution followed by a depthwise convolution. This modification is motivated by the inception module in Inception-v3 that 1×1 convolution is done first before any n×n spatial convolutions. Thus, it is a bit different from the original one. (n=3 here since 3×3 spatial convolutions are used in Inception-v3.)

Two minor differences:

1. The order of operations: As mentioned, the original depthwise separable convolutions as usually implemented (e.g. in TensorFlow) perform first channel-wise spatial convolution and then perform 1×1 convolution(cross channels) whereas the modified depthwise separable convolution perform 1×1 convolution(cross channels) first then channel-wise spatial convolution. This is claimed to be unimportant because when it is used in stacked setting, there are only small differences appeared at the beginning and at the end of all the chained inception modules.
2. The Presence/Absence of Non-Linearity: In the original Inception Module, there is non-linearity after first operation. In Xception, the modified depthwise separable convolution, there is NO intermediate ReLU non-linearity(non-linearity since )11_Training Deep Neural Networks_VarianceScaling_leaky relu_PReLU_SELU _Batch Normalization_Reusing: https://blog.csdn.net/Linli522362242/article/details/106935910.

3. Overall Architecture

     As in the figure above, SeparableConv is the modified depthwise separable convolution(including Pointwise Convolution and Depthwise Convolution). We can see that SeparableConvs are treated as Inception Modules and placed throughout the whole deep learning architecture.

The modified depthwise separable convolution with different activation units are tested. As from the above figure, the Xception without any intermediate activation has the highest accuracy compared with the ones using either ELU or ReLU (VS Figure 14-18. Skip connection when changing feature map size and depth).

And there are residual (or shortcut/skip) connections, originally proposed by ResNet [3], placed for all flows.
As seen in the architecture, there are residual connections. Here, it tests for Xception using non-residual version(Figure 14-18. Skip connection). From the above figure, we can see that the accuracy is much higher when using residual connections. Thus, the residual connection is extremely important !!!
... ...

https://towardsdatascience.com/review-xception-with-depthwise-separable-convolution-better-than-inception-v3-image-dc967dd42568

##############################################################

     You might wonder why Xception is considered a variant of GoogLeNet, since it contains no inception module at all. Well, as we discussed earlier, an inception module contains convolutional layers with 1 × 1 filters: these look exclusively for cross-channel patterns. However, the convolutional layers that sit on top of them are regular convolutional layers that look both for spatial and cross-channel patterns. So you can think of an inception module as an intermediate between a regular convolutional layer (which considers spatial patterns and cross-channel patterns jointly) and a separable convolutional layer (which considers them separately). In practice, it seems that separable convolutional layers generally perform better.

     Separable convolutional layers use fewer parameters, less memory, and fewer computations than regular convolutional layers, and in general they even perform better, so you should consider using them by default (except after layers with few channels除非在通道较少的层之后).

     The ILSVRC 2016 challenge was won by the CUImage team from the Chinese University of Hong Kong. They used an ensemble of many different techniques, including a sophisticated object-detection system called GBD-Net,21 to achieve a top-five error rate below 3%. Although this result is unquestionably impressive, the complexity of the solution contrasted with the simplicity of ResNets. Moreover, one year later another fairly simple architecture performed even better, as we will see now.

SENet

     The winning architecture in the ILSVRC 2017 challenge was the Squeeze-and-Excitation Network (SENet).(Jie Hu et al., “Squeeze-and-Excitation Networks,” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2018): 7132–7141.) This architecture extends existing architectures such as inception networks and ResNets, and boosts their performance. This allowed SENet to win the competition with an astonishing 2.25% top-five error rate! The extended versions of inception networks and ResNets are called SE-Inception and SE-ResNet, respectively. The boost comes from the fact that a SENet adds a small neural network, called an SE block, to every unit in the original architecture (i.e., every inception module or every residual unit), as shown in Figure 14-20.
 Figure 14-20. SE-Inception module (left) and SE-ResNet unit (right)

     An SE block analyzes the output of the unit it is attached to, focusing exclusively on the depth dimension (it does not look for any spatial pattern), and it learns which features are usually most active together. It then uses this information to recalibrate再校准 the feature maps, as shown in Figure 14-21. For example, an SE block may learn that mouths, noses, and eyes usually appear together in pictures: if you see a mouth and a nose, you should expect to see eyes as well. So if the block sees a strong activation in the mouth and nose feature maps, but only mild activation in the eye feature map, it will boost the eye feature map (more accurately, it will reduce irrelevant feature maps). If the eyes were somewhat confused with something else, this feature map recalibration will help resolve the ambiguity.

 Figure 14-21. An SE block performs feature map recalibration

     An SE block is composed of just three layers: a global average pooling layer, a hidden dense layer using the ReLU activation function, and a dense output layer using the sigmoid activation function (see Figure 14-22).
 Figure 14-22. SE block architecture

     As earlier, the global average pooling layer computes the mean activation for each feature map: for example, if its input contains 256 feature maps, it will output 256 numbers representing the overall level of response for each filter. The next layer is where the “squeeze” happens: this layer has significantly fewer than 256 neurons—typically 16 times fewer than the number of feature maps (e.g., 16 neurons)—so the 256 numbers get compressed into a small vector (e.g., 16 dimensions). This is a lowdimensional vector representation (i.e., an embedding) of the distribution of feature responses. This bottleneck step forces the SE block to learn a general representation of the feature combinations (we will see this principle in action again when we discuss autoencoders in Chapter 17). Finally, the output layer takes the embedding and outputs a recalibration vector containing one number per feature map (e.g., 256), each between 0 and 1. The feature maps are then multiplied by this recalibration vector, so irrelevant features (with a low recalibration score) get scaled down while relevant features (with a recalibration score close to 1) are left alone.

https://www.cnblogs.com/bonelee/p/9030092.html
https://blog.csdn.net/qq_36758914/article/details/106918983
https://github.com/taki0112/SENet-Tensorflow/blob/master/SE_Inception_v4.py
https://zhuanlan.zhihu.com/p/65459972

Pretrained Models for Transfer Learning

     If you want to build an image classifier but you do not have enough training data, then it is often a good idea to reuse the lower layers of a pretrained model, as we discussed in https://blog.csdn.net/Linli522362242/article/details/106982127. For example, let’s train a model to classify pictures of flowers, reusing a pretrained Xception model. First, let’s load the dataset using TensorFlow Datasets (see Chapter 13):

import tensorflow_datasets as tfds

dataset, info = tfds.load("tf_flowers", as_supervised=True, with_info=True)

     Note that you can get information about the dataset by setting with_info=True. 

info

info.splits

info.splits['train']

dataset_size = info.splits['train'].num_examples ######## 3670
n_classes = info.features['label'].num_classes   # 5
class_names = info.features['label'].names       ######## ['dandelion', 'daisy', 'tulips', 'sunflowers', 'roses']

print(dataset_size)
print(n_classes)
print(class_names)

     Here, we get the dataset size and the names of the classes. Unfortunately, there is only a "train" dataset, no test set or validation set, so we need to split the training set. The TF Datasets project provides an API for this. For example, let’s take the first 10% of the dataset for testing, the next 15% for validation, and the remaining 75% for training:

test_set_raw, valid_set_raw, train_set_raw = tfds.load(
    "tf_flowers",
    split=[ "train[:10%]", "train[10%:25%]", "train[25%:]" ],
    as_supervised=True
)

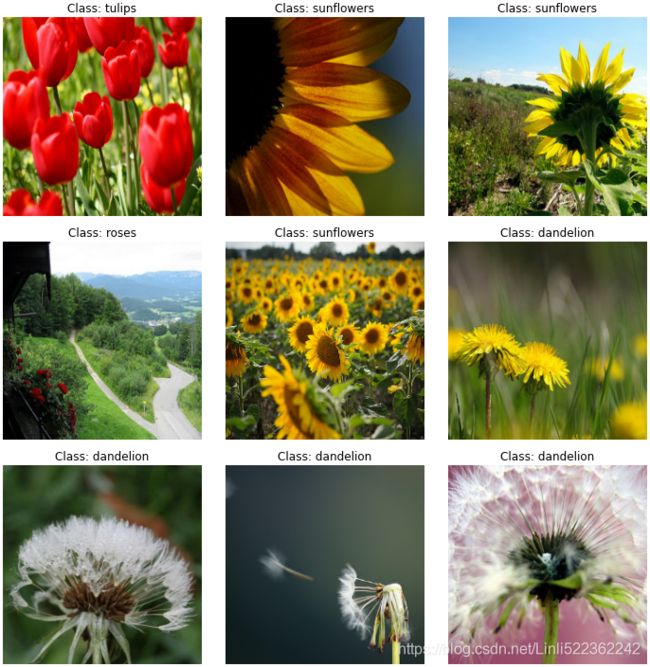
plt.figure( figsize=(12,10) )
index =0
for image, label in train_set_raw.take(9):
  index +=1
  plt.subplot(3,3, index)
  plt.imshow(image)
  plt.title( "Class: {}".format(class_names[label]) )
  plt.axis("off")

 

     Next we must preprocess the images. The CNN expects 224 × 224 images, so we need to resize them. We also need to run the images through Xception’s preprocess_input() function:

def preprocess(image, label):
  resized_image = tf.image.resize(image, [224, 224])
  final_image = keras.applications.xception.preprocess_input( resized_image )
  # The inputs pixel values are scaled between -1 and 1, sample-wise.
  return final_image, label

     Let’s apply this preprocessing function to all three datasets, shuffle the training set, and add batching and prefetching to all the datasets:

def central_crop(image):
  shape = tf.shape(image)   # height OR width
  min_dim = tf.reduce_min([ shape[0], shape[1] ])
  
  # image 2D_array from top-left to bottom-right
  top_crop = (shape[0]-min_dim)//4
  bottom_crop = shape[0] - top_crop
  left_crop = (shape[1]-min_dim)//4
  right_crop = shape[1]-left_crop
  return image[top_crop:bottom_crop, left_crop:right_crop]

def random_crop(image):
  shape = tf.shape(image)
  min_dim = tf.reduce_min([ shape[0], shape[1] ])
  # tf.image.radom_crop :
  #   If a dimension should not be cropped, pass the full size of that dimension
  return tf.image.random_crop( image, size=[min_dim, min_dim, 3]) # 3 since RGB

def preprocess( image, label, randomize=False ):
  if randomize :
    cropped_image = random_crop( image )
    cropped_image = tf.image.random_flip_left_right( cropped_image )
  else:
    cropped_image = central_crop( image )
  resized_image = tf.image.resize( cropped_image, [224,224] )
  # preprocess_input :
  # The inputs pixel values are scaled between -1 and 1, sample-wise.
  final_image = keras.applications.xception.preprocess_input( resized_image )
  return final_image, label

batch_size = 32
train_set = train_set_raw.shuffle(1000).repeat()
train_set = train_set_raw.map( partial(preprocess, randomize=True) ).batch( batch_size ).prefetch(1)
valid_set = valid_set_raw.map( preprocess ).batch( batch_size ).prefetch(1)
test_set = test_set_raw.map( preprocess ).batch( batch_size ).prefetch(1)

     If you want to perform some data augmentation, change the preprocessing function for the training set, adding some random transformations to the training images. For example, use tf.image.random_crop() to randomly crop the images, use tf.image.random_flip_left_right() to randomly flip the images horizontally, and so on (see the “Pretrained Models for Transfer Learning” section of the notebook for an example).

plt.figure( figsize=(12,12) )

for X_batch, y_batch, in train_set.take(1):
  for index in range(9):
    plt.subplot( 3,3, index+1 )
    # X_batch[index]/2 + 0.5 changes color values
    plt.imshow( X_batch[index]/2 + 0.5 ) 
    # index( instance's index ) ==> y_batch[index] == class index
    plt.title("Class: {}".format( class_names[y_batch[index]] ) )
    plt.axis("off")

plt.show()

 

     The keras.preprocessing.image.ImageDataGenerator class makes it easy to load images from disk and augment them in various ways: you can shift each image, rotate it, rescale it, flip it horizontally or vertically, shear it, or apply any transformation function you want to it. This is very convenient for simple projects. However, building a tf.data pipeline has many advantages: it can read the images efficiently (e.g., in parallel) from any source, not just the local disk; you can manipulate the Dataset as you wish; and if you write a preprocessing function based on tf.image operations, this function can be used both in the tf.data pipeline and in the model you will deploy to production (see Chapter 19).

plt.figure( figsize=(12,12) )

for X_batch, y_batch in test_set.take(1):
  for index in range(9):
    plt.subplot(3,3,index+1)
    plt.imshow( X_batch[index]/2 +0.5)
    plt.title( "Class: {}".format( class_names[y_batch[index]] ) )
    plt.axis("off")

plt.tight_layout()
plt.show()

     Next let’s load an Xception model, pretrained on ImageNet. We exclude the top of the network by setting include_top=False: this excludes the global average pooling layer and the dense output layer. We then add our own global average pooling layer, based on the output of the base model, followed by a dense output layer with one unit per class, using the softmax activation function. Finally, we create the Keras Model:

# load the Xception model, pretrained on ImageNet
base_model = keras.applications.xception.Xception( weights="imagenet", 
                                                   include_top=False )
avg = keras.layers.GlobalAveragePooling2D()( base_model.output )
# n_classes = info.features['label'].num_classes   # 5
output = keras.layers.Dense( n_classes, activation="softmax" )(avg)
           # model = Model( data_input, label_output)
model = keras.models.Model( inputs=base_model.input, outputs=output )

for index, layer in enumerate( base_model.layers ):
  print( index, layer.name )

     

     As explained in
cp11_Training Deep Neural Networks_VarianceScaling_leaky relu_PReLU_SELU _Batch Normalization_Reusing
 https://blog.csdn.net/Linli522362242/article/details/106935910 
cp11_Training Deep NN_2_transfer learning_split_datase_RBMs_Momentum_Nesterov AccelerG_AdaGrad_RMSProp
https://blog.csdn.net/Linli522362242/article/details/106982127, it’s usually a good idea to freeze the weights of the pretrained layers, at least at the beginning of training: 
     Now you could train model_B_on_A for task B, but since the new output layer was initialized randomly it will make large errors (at least during the first few epochs), so there will be large error gradients that may wreck the reused weights. To avoid this, one approach is to freeze the reused layers during the first few epochs, giving the new layer some time to learn reasonable weights. To do this, set every layer’s trainable attribute to False and compile the modelhttps://blog.csdn.net/Linli522362242/article/details/106982127:
Figure 11-4. Reusing pretrained layers

 freeze the reused layers during the first 5 epochs, giving the new layer some time to learn reasonable weights

for layer in base_model.layers:
  layer.trainable = False

optimizer = keras.optimizers.SGD( learning_rate=0.2, ######
                                  momentum=0.9, decay=0.01 )
model.compile( loss="sparse_categorical_crossentropy", optimizer=optimizer,
              metrics=["accuracy"] )
# dataset_size = info.splits['train'].num_examples ######## 3670
# batch_size = 32
#  the next 15% for validation, and the remaining 75% for training
history = model.fit( train_set,
                     steps_per_epoch=int(0.75 * dataset_size / batch_size),
                     validation_data=valid_set, # tuple `(x_val, y_val)` of Numpy arrays or tensors
                     validation_steps=int(0.15 * dataset_size / batch_size),
                     epochs=5 )#######

 

run out of data? 

solution: 

 freeze the reused layers during the first 5 epochs, giving the new layer some time to learn reasonable weights

epochs=5
batch_size =32
train_set = train_set_raw.shuffle(1000) # since epochs=5
train_set = train_set_raw.repeat(epochs).map( partial(preprocess, randomize=True) ).batch( batch_size ).prefetch(1)
valid_set = valid_set_raw.repeat(epochs).map( preprocess ).batch( batch_size ).prefetch(1)
test_set = test_set_raw.map( preprocess ).batch( batch_size ).prefetch(1)

for layer in base_model.layers:
  layer.trainable = False

optimizer = keras.optimizers.SGD( lr=0.2, ######
                                  momentum=0.9, decay=0.01 )
model.compile( loss="sparse_categorical_crossentropy", optimizer=optimizer,
              metrics=["accuracy"] )
# dataset_size = info.splits['train'].num_examples ######## 3670
# batch_size = 32
#  the next 15% for validation, and the remaining 75% for training
history = model.fit( train_set,
                     steps_per_epoch=int(0.75 * dataset_size / batch_size),
                     validation_data=valid_set, # tuple `(x_val, y_val)` of Numpy arrays or tensors
                     validation_steps=int(0.15 * dataset_size / batch_size),
                     epochs=epochs )#######

from google.colab import drive
drive.mount('/content/gdrive')

 

model.save("/content/gdrive/My Drive/Colab Notebooks/Xception_CNN_model.h5")
#model = tf.keras.models.load_model("/content/gdrive/My Drive/Colab Notebooks/Xception_CNN_model.h5")

 

history.history

 

hist=history.history
import pickle
with open('/content/gdrive/My Drive/Colab Notebooks/Xception_CNN_model_History5.hdf5', 'wb') as histFile:
  pickle.dump( hist, histFile)
 
# with open('/content/gdrive/My Drive/Colab Notebooks/Xception_CNN_model_History5.hdf5', 'rb') as histFile:
#   hist5=pickle.load(histFile)
# hist5

 
5 epochs

# https://www.tensorflow.org/api_docs/python/tf/keras/callbacks/ModelCheckpoint
# mode = "auto"
# monitor='val_loss' #default
filepath="/content/gdrive/My Drive/Colab Notebooks/Xception_CNN_model.{epoch:02d}.hdf5"
checkpoint_cb = tf.keras.callbacks.ModelCheckpoint(filepath,
                                                   save_freq="epoch",
)
from tensorflow.keras.models import load_model
callbacks_list = [checkpoint_cb]

   Since our model uses the base model’s layers directly, rather than the base_model object itself, setting base_model.trainable=False would have no effect.

Finally, we can compile the model and start training:

for layer in base_model.layers:
    layer.trainable = True    ######

optimizer = keras.optimizers.SGD( learning_rate=0.01,          ######
                                  momentum=0.9, nesterov=True, ######
                                  decay=0.001)
model.compile( loss="sparse_categorical_crossentropy", optimizer=optimizer,
               metrics=["accuracy"] )
history = model.fit( train_set,
                     steps_per_epoch=int(0.75 * dataset_size / batch_size),
                     validation_data=valid_set,
                     validation_steps=int(0.15 * dataset_size / batch_size),
                     epochs=40 ) ######

 run out of data? 

solution: 

epochs=40 #40
batch_size = 32
train_set = train_set_raw.shuffle(1000).repeat() # since epochs=40
train_set = train_set_raw.repeat(epochs).map( partial(preprocess, randomize=True) ).batch( batch_size ).prefetch(1)
valid_set = valid_set_raw.repeat(epochs).map( preprocess ).batch( batch_size ).prefetch(1)
test_set = test_set_raw.map( preprocess ).batch( batch_size ).prefetch(1)

for layer in base_model.layers:
    layer.trainable = True    ######


optimizer = keras.optimizers.SGD( learning_rate=0.01,          ######
                                  momentum=0.9, nesterov=True, ######
                                 
                                  decay=0.001)
model.compile( loss="sparse_categorical_crossentropy", optimizer=optimizer,
               metrics=["accuracy"] )
history = model.fit( train_set,
                     steps_per_epoch=int(0.75 * dataset_size / batch_size),
                     validation_data=valid_set,
                     validation_steps=int(0.15 * dataset_size / batch_size),
                     callbacks=[callbacks_list],##########
                     #initial_epoch=5,######
                     epochs=epochs ) ######

 ... ...
... ...

  This will be very slow, unless you have a GPU. If you do not, then you should run this chapter’s notebook in Colab, using a GPU runtime (it’s free!). See the instructions at https://github.com/ageron/handson-ml2. OR https://blog.csdn.net/Linli522362242/article/details/114239076

     After training the model for a few epochs, its validation accuracy should reach about 75–80% and stop making much progress. This means that the top layers are now pretty well trained, so we are ready to unfreeze all the layers (or you could try unfreezing just the top ones) and continue training (don’t forget to compile the model when you freeze or unfreeze layers). This time we use a much lower learning rate to avoid damaging the pretrained weights:

for layer in base_model.layers:
    layer.trainable = True    ######

optimizer = keras.optimizers.SGD( learning_rate=0.01,          ######
                                  momentum=0.9, nesterov=True, ######
                                  decay=0.001)
model.compile( loss="sparse_categorical_crossentropy", optimizer=optimizer,
               metrics=["accuracy"] )
history = model.fit( train_set,
                     steps_per_epoch=int(0.75 * dataset_size / batch_size),
                     validation_data=valid_set,
                     validation_steps=int(0.15 * dataset_size / batch_size),
                     epochs=40 ) ######

     It will take a while, but this model should reach around 95% accuracy on the test set. With that, you can start training amazing image classifiers! But there’s more to computer vision than just classification. For example, what if you also want to know where the flower is in the picture? Let’s look at this now.

Classification and Localization

     Localizing an object in a picture can be expressed as a regression task, as discussed in 10_Introduction to Artificial Neural Networks w Keras1_HuberLoss_astype_dtype_DNN_MLP_G.gv.pdf_EMA(exponentially weighted moving average) https://blog.csdn.net/Linli522362242/article/details/106433059:(First, MLPs can be used for regression tasks. If you want to predict a single value (e.g., the price of a house, given many of its features), then you just need a single output neuron: its output is the predicted value. For multivariate regression (i.e., to predict multiple values at once), you need one output neuron per output dimension. For example, to locate the center of an object in an image, you need to predict 2D coordinates, so you need two output neurons. If you also want to place a bounding box around the object, then you need two more numbers: the width and the height of the object. So, you end up with four output neurons.) to predict a bounding box around the object, a common approach is to predict the horizontal and vertical coordinates of the object’s center, as well as its height and width. This means we have four numbers to predict. It does not require much change to the model; we just need to add a second dense output layer with four units (typically on top of the global average pooling layer), and it can be trained using the MSE loss:

import tensorflow_datasets as tfds

dataset, info = tfds.load("tf_flowers", as_supervised=True, with_info=True)

dataset_size = info.splits['train'].num_examples ######## 3670
n_classes = info.features['label'].num_classes   # 5
class_names = info.features['label'].names       ######## ['dandelion', 'daisy', 'tulips', 'sunflowers', 'roses']

test_set_raw, valid_set_raw, train_set_raw = tfds.load(
    "tf_flowers",
    split=[ "train[:10%]", "train[10%:25%]", "train[25%:]" ],
    as_supervised=True
)

def preprocess(image, label):
  resized_image = tf.image.resize(image, [224, 224])
  final_image = keras.applications.xception.preprocess_input( resized_image )
  # The inputs pixel values are scaled between -1 and 1, sample-wise.
  return final_image, label

from functools import partial
from tensorflow import keras
import tensorflow as tf

def central_crop(image):
  shape = tf.shape(image)   # height OR width
  min_dim = tf.reduce_min([ shape[0], shape[1] ])
  
  # image 2D_array from top-left to bottom-right
  top_crop = (shape[0]-min_dim)//4
  bottom_crop = shape[0] - top_crop
  left_crop = (shape[1]-min_dim)//4
  right_crop = shape[1]-left_crop
  return image[top_crop:bottom_crop, left_crop:right_crop]

def random_crop(image):
  shape = tf.shape(image)
  min_dim = tf.reduce_min([ shape[0], shape[1] ])
  # tf.image.radom_crop :
  #   If a dimension should not be cropped, pass the full size of that dimension
  return tf.image.random_crop( image, size=[min_dim, min_dim, 3]) # 3 since RGB

def preprocess( image, label, randomize=False ):
  if randomize :
    cropped_image = random_crop( image )
    cropped_image = tf.image.random_flip_left_right( cropped_image )
  else:
    cropped_image = central_crop( image )
  resized_image = tf.image.resize( cropped_image, [224,224] )
  # preprocess_input :
  # The inputs pixel values are scaled between -1 and 1, sample-wise.
  final_image = keras.applications.xception.preprocess_input( resized_image )
  return final_image, label

batch_size = 32
train_set = train_set_raw.shuffle(1000).repeat()
train_set = train_set_raw.map( partial(preprocess, randomize=True) ).batch( batch_size ).prefetch(1)
valid_set = valid_set_raw.map( preprocess ).batch( batch_size ).prefetch(1)
test_set = test_set_raw.map( preprocess ).batch( batch_size ).prefetch(1)

#########################################################################
# load the Xception model, pretrained on ImageNet
# this excludes the global average pooling layer and the dense output layer
base_model = keras.applications.xception.Xception( weights="imagenet", 
                                                   include_top=False )
# computes the average of each feature map separately
# reduces the number of parameters in the network and limits the risk of overfitting
avg = keras.layers.GlobalAveragePooling2D()(base_model.output)

# n_classes = info.features['label'].num_classes   # 5
class_output = keras.layers.Dense( n_classes, activation="softmax" , name="class_ouput")(avg)
# 4 output neurons: horizontal and vertical coordinates of the object’s center, 
# as well as its height and width. 
loc_output = keras.layers.Dense(4, name="loc_output")(avg)

model2 = keras.models.Model(inputs = base_model.input, 
                            outputs=[class_output, #main_out_loss
                                     loc_output] ) #aux_output_loss

optimizer = keras.optimizers.SGD( lr=0.2, ######
                                  momentum=0.9, decay=0.01 )

# (if we pass a single loss, Keras will assume that the same loss must be used 
# for all outputs). By default, Keras will compute all these losses and simply 
# add them up to get the final loss used for training. We care much more about 
# the main output than about the auxiliary output (as it is just used for 
# regularization), so we want to give the main output’s loss a much greater 
# weight. # https://blog.csdn.net/Linli522362242/article/details/106582512
model2.compile(loss=["sparse_categorical_crossentropy", # for classification
                     "mse"],                            # for regression
                    # class_output, loc_output
               loss_weights=[0.8, 0.2], #depends on what you care most about
               # loss(Total)=0.4753 =
               # main_out_loss*loss_weight[0] + aux_output_loss*loss_weight[1] 
               #                   = 0.4245 * 0.9 + 0.9320*0.1
               optimizer = optimizer, metrics=["accuracy"])
#########################################################################

def add_random_bounding_boxes( images, labels ):
  #tf.shape(images): [224,224]
  fake_bboxes = tf.random.uniform([ tf.shape(images)[0],4 ]) #shape: (224,4)
       # images, (class_labels, bounding_boxes)
  return images, (labels, fake_bboxes) # image_dataset, (target_labels, target_bboxes)

fake_train_set = train_set.take(5).repeat(2).map( add_random_bounding_boxes )

model2.fit(fake_train_set, steps_per_epoch=5, epochs=2)

 Epoch 1/2 5/5 [==============================] - 107s 21s/step - loss: 1.0512 - class_ouput_loss: 1.2132 - loc_output_loss: 0.4031 - class_ouput_accuracy: 0.5188 - loc_output_accuracy: 0.2250
Epoch 2/2 5/5 [==============================] - 107s 21s/step - loss: 0.1868 - class_ouput_loss: 0.1778 - loc_output_loss: 0.2227 - class_ouput_accuracy: 0.9625 - loc_output_accuracy: 0.2688

     But now we have a problem: the flowers dataset does not have bounding boxes around the flowers. So, we need to add them ourselves. This is often one of the hardest and most costly parts of a Machine Learning project: getting the labels. It’s a good idea to spend time looking for the right tools. To annotate images with bounding boxes, you may want to use an open source image labeling tool like VGG Image Annotator, LabelImg, OpenLabeler, or ImgLab, or perhaps a commercial tool like LabelBox or Supervisely. You may also want to consider crowdsourcing platforms such as Amazon Mechanical Turk if you have a very large number of images to annotate. However, it is quite a lot of work to set up a crowdsourcing platform, prepare the form to be sent to the workers, supervise them, and ensure that the quality of the bounding boxes they produce is good, so make sure it is worth the effort. If there are just a few thousand images to label, and you don’t plan to do this frequently, it may be preferable to do it yourself. Adriana Kovashka et al. wrote a very practical paper(Adriana Kovashka et al., “Crowdsourcing in Computer Vision,” Foundations and Trends in Computer Graphics and Vision 10, no. 3 (2014): 177–243.) about crowdsourcing in computer vision. I recommend you check it out, even if you do not plan to use crowdsourcing.

     Let’s suppose you’ve obtained the bounding boxes for every image in the flowers dataset (for now we will assume there is a single bounding box per image). You then need to create a dataset whose items will be batches of preprocessed images along with their class labels and their bounding boxes. Each item should be a tuple of the form (images, (class_labels, bounding_boxes)). Then you are ready to train your model!

     The bounding boxes should be normalized so that the horizontal and vertical coordinates, as well as the height and width, all range from 0 to 1. Also, it is common to predict the square root of the height and width rather than the height and width directly: this way, a 10-pixel error for a large bounding box will not be penalized as much as a 10-pixel error for a small bounding box.

def add_random_bounding_boxes( images, labels ):
  #tf.shape(images): [224,224]
  fake_bboxes = tf.random.uniform([ tf.shape(images)[0],4 ]) #shape: (224,4)
       # images, (class_labels, bounding_boxes)
  return images, (labels, fake_bboxes) # image_dataset, (target_labels, target_bboxes)

fake_train_set = train_set.take(5).repeat(2).map( add_random_bounding_boxes )

model.fit(fake_train_set, steps_per_epoch=5, epochs=2)

     The MSE often works fairly well as a cost function to train the model, but it is not a great metric to evaluate how well the model can predict bounding boxes. The most common metric for this is the Intersection over Union (IoU): the area of overlap between the predicted bounding box and the target bounding box, divided by the area of their union (see Figure 14-23). In tf.keras, it is implemented by the tf.keras.metrics.MeanIoU class.
Figure 14-23. Intersection over Union (IoU) metric for bounding boxes

     Classifying and localizing a single object is nice, but what if the images contain multiple objects (as is often the case in the flowers dataset)?

Object Detection

https://blog.csdn.net/Linli522362242/article/details/108669444