CNN的实现(附代码)
前言
前文已经单独实现了卷积层和池化层,现在来组合这些层,搭建进行手写数字识别的CNN。
这个简单的CNN网络构成如下。
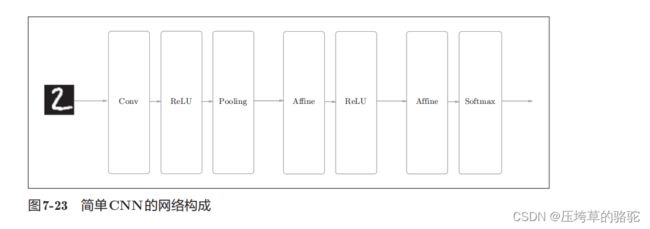
网络的构成是“Convolution - ReLU - Pooling -Affine - ReLU - Affine - Softmax”,我们将它实现为名为SimpleConvNet的类。
该网络的参数
• input_dim―输入数据的维度:(通道,高,长)
• conv_param―卷积层的超参数(字典)。
字典的关键字如下:
filter_num―滤波器的数量
filter_size―滤波器的大小
stride―步幅
pad―填充
• hidden_size―隐藏层(全连接)的神经元数量
• output_size―输出层(全连接)的神经元数量
• weitght_int_std―初始化时权重的标准差
卷积层的超参数通过名为conv_param的字典传入。我们设想它会
像{‘filter_num’:30,‘filter_size’:5, ‘pad’:0, ‘stride’:1}。
这个CNN网络的初始化分为三个部分。
第一部分:取出初始化传入卷积层的超参数,并计算卷积层的输出大小
class SimpleConvNet:
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num':30, 'filter_size':5,'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size/2) *(conv_output_size/2))
第二部分:权重参数的初始化,包括第一层卷积层和两个全连接层的权重和偏置。分别为W1、b1、w2、b2、w3、b3
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
第三步:生成对应的层,向有序字典(OrderedDict)的layers中添加层。只有最后的SoftmaxWithLoss层被添加到别的变量lastLayer
# 生成层
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
self.last_layer = SoftmaxWithLoss()
以上就是SimpleConvNet的初始化中进行的处理。每一层的单独的具体实现已经在前面文中提到,为构建一个简单的CNN网络,每一层各司其职。
像这样进行初始化后,进行推理的predict方法和求损失函数的loss方法调用如下。
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
"""求损失函数
参数x是输入数据、t是教师标签
"""
y = self.predict(x)
return self.last_layer.forward(y, t)
predict方法从头开始依次调用已添加的层,并将结果传递给下一层。
接下来是基于误差反向传播求梯度
def gradient(self, x, t):
"""求梯度(误差反向传播法)
Parameters
----------
x : 输入数据
t : 教师标签
Returns
-------
具有各层的梯度的字典变量
grads['W1']、grads['W2']、...是各层的权重
grads['b1']、grads['b2']、...是各层的偏置
"""
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
因为每一层的误差正向传播和反向传播已经在各层实现,也就是forward()和backward()方法,只需要依次调用每一层的方法即可,最后将每一层中各个权重参数的梯度保存到grads字典中。
simple_convnet类如下
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import pickle
import numpy as np
from collections import OrderedDict
from common.layers import *
from common.gradient import numerical_gradient
class SimpleConvNet:
"""简单的ConvNet
conv - relu - pool - affine - relu - affine - softmax
Parameters
----------
input_size : 输入大小(MNIST的情况下为784)
hidden_size_list : 隐藏层的神经元数量的列表(e.g. [100, 100, 100])
output_size : 输出大小(MNIST的情况下为10)
activation : 'relu' or 'sigmoid'
weight_init_std : 指定权重的标准差(e.g. 0.01)
指定'relu'或'he'的情况下设定“He的初始值”
指定'sigmoid'或'xavier'的情况下设定“Xavier的初始值”
"""
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
# 初始化权重
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * \
np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# 生成层
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
self.last_layer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
"""求损失函数
参数x是输入数据、t是教师标签
"""
y = self.predict(x)
return self.last_layer.forward(y, t)
def accuracy(self, x, t, batch_size=100):
if t.ndim != 1 : t = np.argmax(t, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i*batch_size:(i+1)*batch_size]
tt = t[i*batch_size:(i+1)*batch_size]
y = self.predict(tx)
y = np.argmax(y, axis=1)
acc += np.sum(y == tt)
return acc / x.shape[0]
def numerical_gradient(self, x, t):
"""求梯度(数值微分)
Parameters
----------
x : 输入数据
t : 教师标签
Returns
-------
具有各层的梯度的字典变量
grads['W1']、grads['W2']、...是各层的权重
grads['b1']、grads['b2']、...是各层的偏置
"""
loss_w = lambda w: self.loss(x, t)
grads = {}
for idx in (1, 2, 3):
grads['W' + str(idx)] = numerical_gradient(loss_w, self.params['W' + str(idx)])
grads['b' + str(idx)] = numerical_gradient(loss_w, self.params['b' + str(idx)])
return grads
def gradient(self, x, t):
"""求梯度(误差反向传播法)
Parameters
----------
x : 输入数据
t : 教师标签
Returns
-------
具有各层的梯度的字典变量
grads['W1']、grads['W2']、...是各层的权重
grads['b1']、grads['b2']、...是各层的偏置
"""
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 设定
grads = {}
grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
def save_params(self, file_name="params.pkl"):
params = {}
for key, val in self.params.items():
params[key] = val
with open(file_name, 'wb') as f:
pickle.dump(params, f)
def load_params(self, file_name="params.pkl"):
with open(file_name, 'rb') as f:
params = pickle.load(f)
for key, val in params.items():
self.params[key] = val
for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
self.layers[key].W = self.params['W' + str(i+1)]
self.layers[key].b = self.params['b' + str(i+1)]
参考
《深度学习入门:基于Python的理论与实现 》斋藤康毅