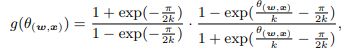CVPR2018 Spotlight 《Decoupled Networks》读后感
- Deep
- Learning
- Decoupled
- Learning
- Hyperspherical
- Learning
- 机器学习
- 神经网络
- Hyperspherical
- Learning
- Decoupled
- Learning
首先要明确的最顶层的概念是:CNN是一个visual representation learning的过程,所有的convolutional filters wi是学到的features template,每一个convolutional操作就是一个template matching,通过dot-product这种计算方式来量化滑窗位置的image patch xi与convolutional filter(feature template)之间的相似度。这个相似度以一个一维实数表示。
那么,我们期待学到什么样的feature(filters)才是最好的feature呢?从分类的角度出发,我们希望一个feature能够很好地discriminate & generalize on 两件事(1). Intra-class variations,即类内差距;(2). Inter-class variations, 即类间差距(semantic difference)。(从分类的角度推广到广义的机器学习任务,则可以认为intra-class variation是wi与xi之间的engery,而inter-class variation是wi与xi之间的similarity。)
显然,传统的CNN基于dot-product based 的相似度计算,只能获得一个一维的实数值,又如何能够用一个一维实数去explicitly地表征两种variations呢?这种表征不力的现象,可以理解为dot-product的计算“couples”两种本该分开的variations,从而限制了传统convolution操作的discrimination & generalization power。所谓“couples”,就是传统CNN make a strong assumption that two variations can be represented via a multiplications of norms and cosines into one single value (即dot-product的操作)。
自然地,为了提高convolutional operations的discrimiantion & generalization power,我们就要把coupled的dot-product进行“de-couple(解耦)”。
De-couple(解耦)最直接的理解,就是原本由一个实数表示的卷积(dot-product)结果(即w与x的相似度),现在由两个量,norm (magnitude function h())& angle (angualr function g())的相乘来表示。传统Convolution,也即dot-product based convolution,其实也是h()*g(),只不过h()被默认是||w||*||x||, g() = cos(θ(w,x))。decouple的操作,就是给h()和g()的设计有了更多的自由度flexibility,可以做到更加task-specific。
那么,如何de-couple呢?de-couple之后,如何分别反应intra- & inter-class variations呢?这里就要引入几何理解,即:
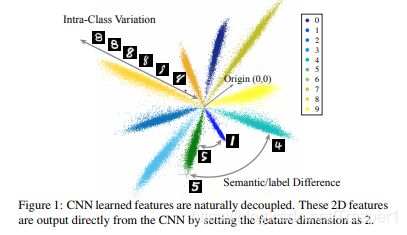
1):features的norm(范数,即强度magnitude)反应intra-class variation;
2):feature的angle(角度)反应inter-class variation。(这里提到的features,指的是卷积操作之后得到的值。原本的dot-product based得到的是一个实数,而现在是分别用范数值和角度值这两个量来反映wi和xi的相似度)
如上图所示,对与一个0-9数字10分类的问题,不同的类别反应为角度分开,类间差距越大,夹角越大;而相同类别之内,比如数字“8”,在这个方向上norm越大的feature表示类内相似度越高,即xi与模板wi(标准的“8”)越像,相似度越大。
而所谓“coupled”与“de-coupled”卷积操作,在表示上无非如此:
Coupled: ;
dot-product的几何意义决定了传统convolution的h()和g()默认为||w||*||x||和cos(θ(w,x)),然后二者相乘。
De-coupled:;两个function h() and g()分别来计算feature magnitude and angular similarity,也即intra- and inter-class variations,把原本乘在一起的量分开为二。
所以,现在一切的工作,就是把convolution操作由原先的一股脑儿的dot-product,变成基于w和x的两个分开的function:magnitude function h()and angular function g()的设计和计算。
本文提出这两个function,也即operator的设计,由两类方案:
1)bounded operators:好处在于 faster convergence and better robustness against adversarial attacks;
2)unbounded operators:好处在于better representatioanl power。
1. Design of magnitude function h(||w||,||x||):
有两种设计:
1)No ||w||: Removing w from h() indicates that all kernels (operators) are assigned with equal importance, which encorages the network to make decision based on as many kernels as possible and therefore may take the network generalize better.
2) with ||w|| (weighted decoupled operators): incorporating the kernel importance to the network learning can improve the representatioanl power and may be useful when dealing with a large-scale dataset with numerous categories.
实验证明unweighted operators,即no ||w||的性能要优于weighted。
下面开始介绍所有的h()的设计(no ||w||):分为bounded and unbounded两大类
1)bounded:
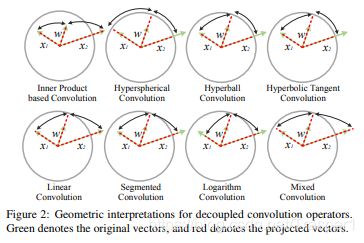
a). Hyperspherical Convolution (SphereConv): projecting w and x to a hypersphere and then performing dot-product
![]()
b). Hyperball Convolution (BallConv): more robust and flexible than SphereConv in the sense that SphereConv may amplify the x with very small ||x||:
c). Hyperbolic Tangent Convolution (TanhConv): smooth version of BallConv, more convergence gain due to its smoothness:
2) unbounded:
a). Linear Convolution (LinearConv):
![]()
b). Segmented Convolution (SegConv): is a flexible multi-range linear function corresponding to ||x||, both Linear and BallConv are special cases for SegConv:
c). Logarithm Convolution (LogConv): smooth
![]()
d). Mixed Convolution (MixConv): combo of any forms above, better flexibility:
上图给出了不同decoupled operator的几何解释。途中绿色线条是原先的filter (template)w,patch x1 和 patch x2。我们的目标是某个operator能够最好地从magnitude & angular的角度来区别开x1和x2,也即让x1和x2的norm(也即在球面上的geodesic distance)以及夹角的差别都最大(因为这里只讨论no ||w||的情况,所以所有的w已经被normalized到了球面上)。可见,SphereConv把norm上的区别抹掉了,即intra-variation不够敏感,但是它带来的夹角x1与w and x2与w的夹角(即inter-class variation)差别最大。这里,夹角与在sphere表面上的geodesic distance也成正相关。
2. Design of angular function g(θ(w,x)):
a). Linear Angular Activation:
b). Cosine Angular Activation:dot-product is this
![]()
c). Sigmoid Angular Activation:
d). Square Cosine Angular Activation:
此外,作者还提到了learnable decoupled operators。怎么理解呢?普通的dot-product based conv的参数是w,此外再无参数。而learnable decoupled operators的flexibility和generalization capability体现在更好的参数化。也即除了w之外,h()和g()中也包含可学习的参数,这些参数可以一并由back-propagation进行优化。