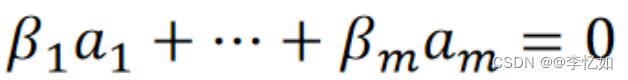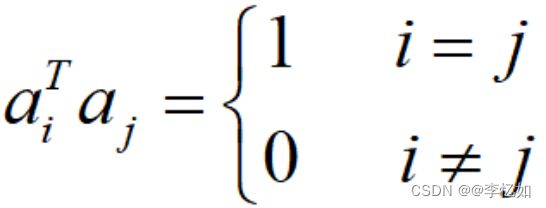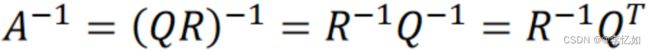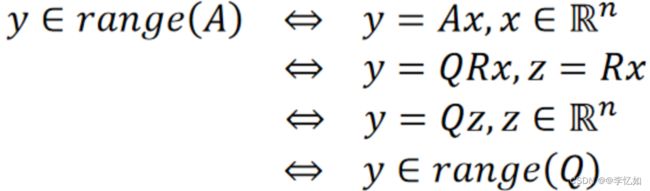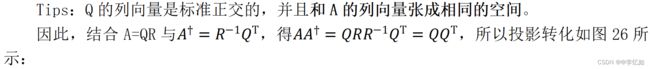最优化方法——QR分解
目录
系列文章目录
一、问题
二、实验思路综述
1.实验工具及算法
2.实验数据
3.实验目标
4.实验步骤
三、相关线性代数知识导入
1.线性无关与基
2.标准正交
3.Gram-Schmidt(正交化)算法
四、QR分解
1.Gram-Schmidt QR
1.1 算法原理
1.2 算法流程
1.3 复杂度分析
1.4 Gran-Schmidt QR实现
1.5 稳定性测试
2.Modified Gram-Schmidt QR
2.1 算法原理
2.2 算法流程
2.3 复杂度分析
2.4 Modified Gram-Schmidt QR实现
2.5 稳定性测试
3.Householder
3.1 算法原理
3.2 算法流程
3.3 复杂度分析
3.4 Householder实现
3.5 稳定性分析
五、逆矩阵的判断与求解
1.逆的判断
2.逆矩阵求解
3.QR分解后求逆矩阵
六、QR分解补充与拓展
1.Givens QR分解
1.1 算法简介
1.2 Givens QR实现
1.3 稳定性分析
1.4 Givens QR在稀疏矩阵中的优势
2.QR分解应用
2.1 QR分解求解线性方程组
2.2 QR分解求解最小二乘问题
2.3 QR分解推导列向量线性无关的矩阵在值域上的投影
3.Python QR分解代码
4.不同语言与平台对QR分解的影响
七、实验小结
1.QR分解总结
2. 参考资料
系列文章目录
本系列博客重点在最优化方法的概念原理与代码实践(有问题欢迎在评论区讨论指出,或直接私信联系我)。
代码可以全抄 大家搞懂原理与流程去复现才是有意义的!!!
第一章 最优化方法——K-means实现手写数字图像聚类_@李忆如的博客-CSDN博客
第二章 最优化方法——QR分解
梗概
本篇博客主要介绍QR分解的原理与流程,分别使用Matlab、Pycharm分别实现了Gram-Schmidt、修正GS、Householder、Givens四种方法对给定矩阵进行对QR分解并进行正交性偏差分析并对比,并在QR分解的应用上进行了拓展(内附数据集和python及matlab代码)。
一、问题
读取附件MatrixA.mat文件中的矩阵A,利用Gram–Schmidt(GS)算法对A进行QR分解,GS的Matlab代码如1所示。
(1) 验证GS是否能稳定进行QR分解矩阵A,其Q矩阵是否正交?
图1 Gram–Schmidt算法的Matlab代码
(2) 实现Householder方法QR分解代码,并验证其对矩阵A分解是否稳定?
(3) 读取附件MatrixB.mat文件的方矩阵B,判断其是否可逆?如果可逆,求其逆矩阵。
二、实验思路综述
1.实验工具及算法
本次实验分别使用Matlab、Pycharm分别实现了Gram-Schmidt、修正GS、Householder、Givens四种方法对给定矩阵进行对QR分解并进行正交性偏差分析并对比。
2.实验数据
本次实验使用给定矩阵A(50x50)与矩阵B(100x100)进行实验内容的探究,在拓展内容的探究与尝试中使用了部分网络数据集。
3.实验目标
本次实验要求使用不同方法对给定矩阵A进行QR分解并进行稳定性分析及对比,并对给定矩阵B进行可逆性判断与逆矩阵的求解。
4.实验步骤
本次实验大致流程如表1所示:
表1 实验2流程
| 1.实验思路综述 |
| 2. 相关线性代数知识导入 |
| 3. QR分解的简介与实现 |
| 4. 逆矩阵的判断与求解 |
| 5. 不同方法对比分析与拓展 |
三、相关线性代数知识导入
在正式进行QR分解实验前,需要对核心的线性代数知识进行补充与说明,详情如下:
1.线性无关与基
线性无关:如果n维向量集{a_1,…,a_m}不是线性相关的,即也称线性无关,求解公式如式1所示:
式1 线性组合求解公式
当且仅当解均为0时,n维向量集为线性无关,即不存在一个向量a_i是其它向量的线性组合。
基:n个线性独立的n维向量a_1,…,a_n的集合称为基(basis)。
2.标准正交
标准正交向量:如果n维向量集a_1,…,a_k相互正交,且每个向量的模长都为单位长度1,则称它们是标准正交的,内积定义如式2所示:
式2 标准正交向量内积定义
标准正交基:当k=n时,a_1,…,a_n是n维向量的一个标准正交基。
标准正交分解:如果a_1,…,a_n是一个标准正交基,对于任意n维向量x,若满足式3,则称其为x在标准正交基下的标准正交分解,样例如图1所示:
式3 标准正交分解判别式
图1 标准正交分解样例
3.Gram-Schmidt(正交化)算法
在了解线性无关与标准正交相关定义后,常使用Gram-Schmidt算法对向量进行标准正交化(同时验证向量是否线性无关),算法流程如表2所示,算法过程可视化如图2所示:
表2 Gram-Schmidt算法流程
分析:如果步骤2中未提前结束迭代,那么a_1,…,a_k是线性独立的,而且q_1,…,q_k是标准正交基。如果在第j次迭代中提前结束,说明a_j是a_1,…,a_j−1的线性组合,因此a_1,…,a_k是线性相关的。
当一个矩阵X满足XA=I时,X被称为A的左逆,同理可以定义右逆。
矩阵的逆:如果矩阵A存在左逆和右逆,则左逆和右逆一定相等,此时X称为矩阵的逆(矩阵非奇异),记作A^-1。
矩阵逆的常用证明框架如图3所示:
图3 矩阵逆的证明框架
补充:性质(a)对任意矩阵A都成立,性质(b)对方阵矩阵A都成立。
四、QR分解
QR分解是将一个矩阵A分解成具有标准正交列向量的矩阵Q和上三角矩阵R(对角线元素不为0)的算法。这个分解能够有效的提高计算机求解线性方程、最小二乘问题、带约束的最小二乘问题的效率,有效降低计算复杂度,QR分解形式如图4所示:
图4 QR分解定义形式
一般来说,QR分解根据原理分为Gram-Schmidt、Householder、Givens三种实现方法,详解如下:
1.Gram-Schmidt QR
1.1 算法原理
Gran-Schmidt QR方法是基于正交化定义的方法,实现核心类似数学归纳法,逐列计算Q和R,通过第k步的结果推导到第k+1步。
1.2 算法流程
Gran-Schmidt QR算法流程如表3所示:
表3 Gram-Schmidt QR算法流程
1.3 复杂度分析
1.4 Gran-Schmidt QR实现
根据Gran-Schmidt QR算法原理与流程,编写相关代码及其代码解析如下:
[m,n]=size(A);
if rank(A)~=n
error('该矩阵无法进行进行基于Gram-Schmidt的QR分解!'); %检测参数异常,停止程序
end
Q=zeros(m,n);
R=zeros(n,n);
for k=1:n
R(1:k-1,k)=Q(:,1:k-1)'*A(:,k); %求出R(1,K) - R(K-1,K)
v=A(:,k)-Q(:,1:k-1)*R(1:k-1,k); %求出正交化向量qk~
R(k,k)=norm(v); %求出R(K,K)
Q(:,k)=v/R(k,k);%求出标准正交化向量qk
end1.5 稳定性测试
使用QR分解后得到Q与R,但还需对其分解进行稳定性测试,即测试qk与前面列之间的正交性的偏差,测试标准如式5所示:
式5 QR分解稳定性测试标准
根据正交性偏差的定义,去编写QR分解稳定性测试及绘图代码,如下:
%%正交性偏差验证
E = zeros(1,n);
for k=2:n
max = 0;
for i=1:k-1
temp = abs(Q(:,i)' * Q(:,k));
if temp > max
max = temp;
end
end
E(1,k)=max;
end
plot(E)对实验给定的矩阵A使用Gran-Schmidt QR代码进行QR分解,并进行稳定性检测,正交性偏差趋势如图7所示:
图7 Gran-Schmidt QR分解的稳定性趋势
分析:由于浮点数存储的舍入误差,在一定范围(误差积累)后,随着k增大,ek波动性增大,即Q矩阵逐渐失去正交性,稳定性较低。
2.Modified Gram-Schmidt QR
由上文分析可知,使用Gran-Schmidt QR进行QR分解由于数值计算的精度问题,其计算的误差累积较快,当矩阵维数较高的时候具有较差的稳定性。
其误差影响两个方面,一是矩阵Q的正交性,矩阵的正交性使得其逆矩阵可以直接通过矩阵的转置得到,如果正交性被破坏,那么会造成计算的错误;二是矩阵R元素的精度问题,越往后面计算所得的元素误差越大。总的来说传统方法的误差水平大约为计算机精度的平方根。
因此针对如上问题,在Gran-Schmidt QR进行优化,提出了Modified Gram-Schmidt QR(修正GS)用于QR分解,详解如下:
2.1 算法原理
算法核心:在Gran-Schmidt QR的基础上对剩余向量进行修正
首先让我们观察Gran-Schmidt QR分析误差积累原因,如图8所示:
图8 Gran-Schmidt QR过程可视化
分析:由图8与Gran-Schmidt QR的算法流程分析,由于其进行QR分解是逐列分解,本向量只与之前的向量有关,其他之后的向量不可见。而计算过程中不可避免地引入误差,而后面的向量只有在其被计算的时候才可见,这时误差可能已经积累到一定程度,所以导致其稳定性较差。
故想减小误差积累,提高稳定性,同时也要考虑当前计算向量之后的向量。故Modified Gram-Schmidt QR的主要改进思路为首先选定一个向量作为第一个基准,然后将其余所有向量都投影到该基准的正交空间中。在该正交空间中,对剩下的向量重复前面的工作,那么最后所有的向量都是相互正交的了。过程可视化如图9所示:
图9 Modified Gram-Schmidt QR过程可视化
分析:Modified Gram-Schmidt QR使得从一开始所有的向量都是可见的,这样大部分的计算都在误差尚未积累到较大程度的时候就已经被执行。实际上,MGS的计算量越往后是逐步减少的,因此前面计算积累的误差的影响就不会剧烈地扩散开,所以MGS可以使求得的矩阵Q的正交性更好,同时矩阵R的误差也被控制在计算机精度的水平。
2.2 算法流程
本质上Modified Gram-Schmidt QR与Gran-Schmidt QR是等价的,MGS只是对其计算过程进行了重排(按行计算R的元素,而非按列)。
2.3 复杂度分析
由2.2可知,本质上Modified Gram-Schmidt QR与Gran-Schmidt QR是等价的,只是计算顺序不同,故计算消耗的总和一样,对矩阵A(mxn)进行QR分解的复杂度也约为2mn^2 flops。
2.4 Modified Gram-Schmidt QR实现
根据Modified Gram-Schmidt QR算法原理与流程,编写相关代码及其核心代码解析如下:
% 修正后GS
Q(:,1)=A(:,1)/norm(A(:,1)); %定义第一个向量基准
R(1,1)=norm(A(:,1));
for k=2:n
for i=k:n
A(:,i)=A(:,i)-A(:,i)'*Q(:,k-1)*Q(:,k-1);
end
R(k,k)=norm(A(:,k)); %求出R(K,K)
Q(:,k)=A(:,k)/R(k,k); %求出标准正交化向量qk
end2.5 稳定性测试
对实验给定的矩阵A使用Modified Gram-Schmidt QR代码进行QR分解,并进行稳定性检测,修正前后正交性偏差趋势如图11所示:
图12 修正前后Gram-Schmidt QR分解的稳定性趋势(左为修正前)
分析:由图12可见,修正前Gram-Schmidt QR分解在k>35后正交性偏差开始逐渐增大,由0逐渐增大到近1。而在修正后仅从0逐渐增大到近1.2 x 10^-7。由此,验证了修正后算法有更好的数值计算性能,能有效减少计算机浮点数存储的误差,大大提高稳定性。
3.Householder
对于Modified Gram-Schmidt QR仍存在相对较大的正交性偏差,且算法时间复杂度较高,故提出Householder算法,为QR分解最常用算法,详解如下:
3.1 算法原理
Householder是基于迭代镜面反射的方法,通过构造反射算子,利用映射不断对原矩阵A进行Householder三角化,实现QR分解,一般形式如图13所示,三角化如图14所示:
图13 Householder一般形式
Tips:每个Hi是对称的正交的“反射算子”。
图14 Householder三角化样例
3.2 算法流程
Householder QR算法流程如表4所示:
表4 Householder QR算法流程
3.3 复杂度分析
根据算法流程对Householder QR进行复杂度分析,详情如下:
在第k次循环中,复杂度分析如下:
Ⅰ、乘积:(2(m-k+1)-1)(n-k+1) flops
Ⅱ、外积:(m-k+1)(n-k+1) flops
Ⅲ、减法:(m-k+1)(n-k+1) flops
所以第k次循环的总和消耗即为:4 (m-k+1)(n-k+1) flops。根据以上三点分析,使用Householder QR对矩阵A(mxn)进行QR分解的复杂度计算如式8所示,约为2mn^2 -2/3n^3 flops。
式8 Householder QR分解时间复杂度
3.4 Householder实现
在matlab中,可直接使用库函数[Q,R] = qr(A)使用Householder进行QR分解,用法解析可见:QR 分解 - MATLAB qr - MathWorks 中国
在python中,可直接使用numpy的库函数Q, R = np.linalg.qr(A) 使用Householder进行QR分解,用法解析可见:numpy.linalg.qr — NumPy v1.23 Manual
根据Householder QR算法原理与流程,自己编相关代码及核心代码解析如下:
% %Householder
% for k=1:n
% y = A(k:m,k);
% y1 = y(1,1);
% e1=zeros(m-k+1,1);
% e1(1)=1;
% w = y+sign(y1)*norm(y)*e1;
% v=w/norm(w); % 计算反射算子
% A(k:m,k:n)=A(k:m,k:n)-2*v*(v'*A(k:m,k:n));
% end
% R=A(1:m,1:n);
% [Q,R]=qr(A); %库函数3.5 稳定性分析
对实验给定的矩阵A使用图15代码(Householder算法)进行QR分解,使用图7代码进行稳定性检测,Householder与Modified Gram-Schmidt QR的正交性偏差趋势对比如图16所示:
图16 Householder与MGS的正交性偏差趋势对比
分析:由图可见,使用Modified Gram-Schmidt QR分解在k>40后正交性偏差开始逐渐增大,从0逐渐增大到近1.2 x 10^-7,而Householder算法进行QR分解的正交性偏差从0波动增大到近3.5 x 10^-16,由此,验证了Householder算法有更好的数值计算性能,能减少计算机浮点数存储的误差,大大提高稳定性,且算法复杂度较低,一般效率较高。
五、逆矩阵的判断与求解
1.逆的判断
对于一个矩阵的逆是否存在,有如表5中所示五种常用方法:
表5 逆矩阵存在判断常用方法
| 1.若矩阵行列式不为0,可逆 |
| 2.若矩阵的秩为你,可逆 |
| 3.若存在一个矩阵B,使AB=BA=I,可逆 |
| 4.对于齐次方程AX=0,若方程只有零解,可逆 |
| 5.对于非齐次线性方程AX=b,若方程只有特解,可逆 |
对于实验给定的矩阵B(100x100)进行逆矩阵存在性的判断,以秩判断法为例,代码如下:
if rank(A)~=n
error('该矩阵无法进行进行基于Gram-Schmidt的QR分解!'); %检测参数异常,停止程序
end分析:在输入矩阵B后进行判断,程序正常运行,没有报错退出,证明矩阵B的逆矩阵存在,求解过程如下。
2.逆矩阵求解
在编程实现中矩阵求逆一般使用库函数,在不同语言中均进行了打包,如matlab中可使用inv()求逆矩阵,。具体用法详见:矩阵求逆 - MATLAB inv - MathWorks 中国,用pinv()求伪逆,具体用法详见:Moore-Penrose 伪逆 - MATLAB pinv - MathWorks 中国。
在python中可使用np.linalg.inv()求逆矩阵,具体用法详见:numpy.linalg.inv — NumPy v1.23 Manual,用numpy.linalg.pinv()求伪逆,具体用法详见:numpy.linalg.pinv — NumPy v1.23 Manual。
3.QR分解后求逆矩阵
除了使用库函数求逆,可以使用QR分解推导对应的逆矩阵求解公式,详解如下:
由(1)已经分析出实验给定矩阵B为可逆矩阵(非奇异),故本部分使用QR分解推导B的逆矩阵,公式推导如式9所示:
式9 QR分解推导矩阵的逆
分析:故求B的逆矩阵即使用R(上三角矩阵)的逆乘Q(正交矩阵)的转置即可。
故根据式9编写代码求B矩阵的逆,并用matlab库函数inv()求解B矩阵的逆去验证QR推导求解矩阵的逆的正确性,验证代码如下:
%求逆
A_inv_stand = inv(A);
A_inv = inv(R) * Q';
if A_inv ~=A_inv_stand
error('QR求解得出的逆矩阵有误!');
end分析:运行代码,程序正常执行,QR分解推导公式求解得到与库函数一样的逆矩阵,验证了其求逆矩阵的正确性。
六、QR分解补充与拓展
1.Givens QR分解
除了上文提到的Gram-Schmidt QR、Modified Gram-Schmidt QR、Householder QR之外,还有一种常用的算法用于QR分解——Givens Transformation。
1.1 算法简介
Givens QR是基于迭代旋转变化的算法,基本原理为将原矩阵A的主对角线下方元素经过Givens旋转转置为0,形成R,同时左乘一系列的Givens矩阵得到Q,实现QR分解,一般流程如图19所示:
图19 Givens QR分解一般流程
1.2 Givens QR实现
根据算法简介,编写Givens QR分解代码,核心如下:
function [Q,R]=givenQR(A)
n=size(A,2); %列数
m=size(A,1); %行数
R=A;
Q=eye(m);
for i=1:n-1
for j=i+1:m
x=R(:,i);
rt=givens(x,i,j);%J矩阵
%r=blkdiag(eye(i-1),rt)
Q=Q*rt';
R=rt*R;
end
end
end
function [R,y]=givens(x,i,j)
xi=x(i);
xj=x(j);
r=sqrt(xi^2+xj^2);
cost=xi/r;
sint=xj/r;
R=eye(length(x));
R(i,i)=cost;
R(i,j)=sint;
R(j,i)=-sint;
R(j,j)=cost;
y=x(:);
y([i,j])=[r,0];%sint cost
end1.3 稳定性分析
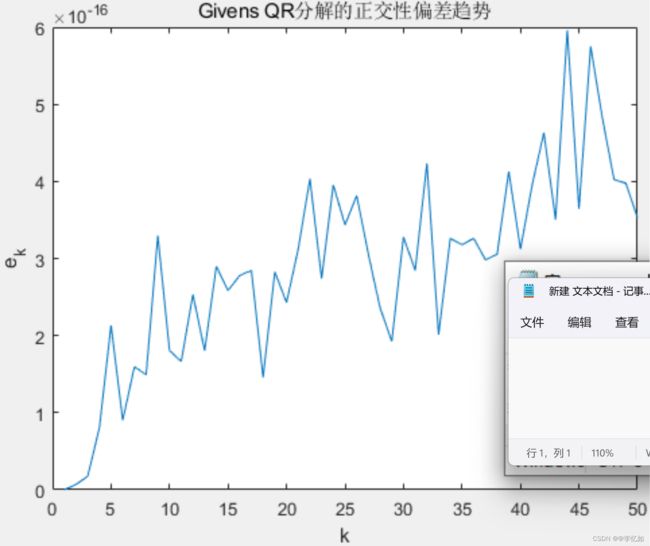
对实验给定的矩阵A使用图19代码(Givens算法)进行QR分解,使用图7代码进行稳定性检测,Givens QR的正交性偏差趋势如图20所示:
图20 Givens QR的稳定性趋势
分析:由图20可见,Givens QR分解的正交性偏差随着k增大而逐渐增大,由0波动增大到近6 x 10^-16。结合图12、16分析,Givens QR分解的稳定性高于GS与修正GS,略低于Householder QR。
1.4 Givens QR在稀疏矩阵中的优势
稀疏矩阵:矩阵中包括较多的零元素
通过对Gram-Schmidt QR、Householder QR及Givens QR的原理分析,不难发现前两种方法由于正交基的计算在稀疏矩阵的运算中会产生大量无效计算,内存开销大,效率低。而Givens QR分解由于其基于迭代旋转变换,仅影响向量的两个分量,不会对零元素做无效操作,故在稀疏矩阵的QR分解中有较好表现,本部分对这一特性进行验证。
因本次实验所给数据(矩阵A与B)均为较稠密矩阵,且维度较小,方法间的差别不大,故使用网络数据稀疏矩阵C(1000x1000)进行探究,在matlab下使用不同方法进行QR分解,每种方法进行20次取平均值,时间数据汇总如表6所示,效果对比如图21所示:
表6 稀疏矩阵下不同QR分解方法的平均运行时间数据汇总
图21 稀疏矩阵下不同QR分解方法效率对比
分析:由表6与图21可见,稀疏矩阵下,Givens QR分解平均运行时间低于GS与Householder QR,效率最优,验证了上述理论的正确性。
2.QR分解应用
对于QR分解的应用,可用QR分解求解线性方程组、最小二乘问题、带约束的最小二乘问题。由QR分解引出的实用简单公式:列向量线性无关的矩阵的伪逆、非奇异矩阵的逆、列向量线性无关的矩阵在值域上的投影。
对于QR分解求非奇异矩阵的逆上文已有详述,在本部分对QR分解的其他应用进行一定解析与探索,详情如下:
2.1 QR分解求解线性方程组
使用QR分解求解线性方程组Ax=b(A为非奇异矩阵),流程如表7所示:
表7 使用QR分解求解线性方程组流程
| 1.首先对A进行QR分解,得到A = QR |
| 2.计算y =Q^Tb |
| 3.通过回代法求解Rx = y |
复杂度分析:其中QR分解复杂度为2n^3,矩阵向量乘法为2n^2,回代法为n^2,所以平均复杂度约为2n^3 flops。
2.2 QR分解求解最小二乘问题
使用QR分解求解最小二乘问题,最优闭式解的推导如图22所示:
图22 QR分解推导最小二乘问题的最优闭式解
复杂度分析:首先对A进行QR分解A=QR(2mn^2 flops),再计算矩阵向量乘积d=Q^Tb(2mn flops),最后通过回代求解Rx=d(n^2 flops),所以平均复杂度为2mn^2 flops。
我们将这种解法应用到吴恩达的《机器学习》课程上的房价预测的数据集上,去检验QR分解对于最小二乘问题求解的正确性,Python代码如下:
import numpy as np
import matplotlib.pyplot as plt
if __name__ == '__main__':
# QR求解最小二乘问题最优闭式解
data = np.loadtxt('ex1data1.txt', delimiter=',') # load data
X = data[:, 0]
y = data[:, 1] # 注意这里得到的y的shape为(m, ),要把它reshape为(m,1)
y = np.reshape(y, (y.shape[0], 1))
plt.scatter(X, y, marker='x', c='r')
# 在X的第一列之前插入元素全为1的列
X = np.column_stack(
(np.ones((X.shape[0], 1)), np.reshape(X, (X.shape[0], 1))))
# QR分解
Q, R = np.linalg.qr(X)
w = np.linalg.linalg.inv(R).dot(Q.T).dot(y)
print(w)
plt.plot(X[:, 1], np.dot(X, w), '-')
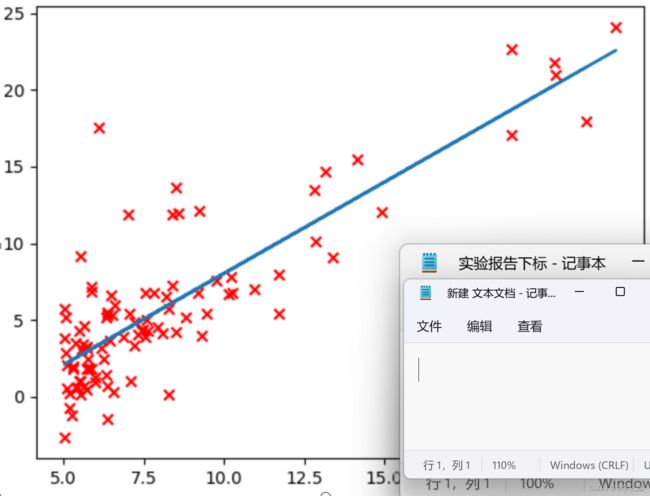
plt.show()效果如图24所示:
图24 QR分解求解最小二乘问题样例
分析:由图24可见,QR分解后通过公式成功将数据拟合出直线,求解出了具体最小二乘问题上的最优闭式解,验证了正确性。
2.3 QR分解推导列向量线性无关的矩阵在值域上的投影
对于有线性无关的矩阵A,Q和A的值域范围相同,证明如图25所示:
图25 Q和A的值域范围相同证明
图26 QR分解推导值域投影
3.Python QR分解代码
在此,对GS、Householder、Givens QR分解在Python上重构,代码如下:
def schmidt_orthogonal(matrix_a):
"""
Gram-Schmidt Orthogonal
:param matrix_a:
:return: matrix_q, matrix_r
"""
# row num: n
# col num: m
n, m = matrix_a.shape
matrix_r = np.zeros([m, m])
orthogonal_list = []
# Iter each cols
for j in range(m):
a = np.reshape(matrix_a[:, j], (n, 1))
for i in range(len(orthogonal_list)):
matrix_r[i][j] = np.matmul(orthogonal_list[i].T,
a)
for i in range(len(orthogonal_list)):
a = a - matrix_r[i][j] * orthogonal_list[i]
# a_norm_2
matrix_r[j][j] = np.int(np.sqrt(np.matmul(a.T, a)))
q = np.true_divide(a, matrix_r[j][j])
orthogonal_list.append(q)
print("Q matrix", np.array(orthogonal_list).T)
matrix_q = np.array(orthogonal_list).T.reshape((n, m))
def householder_reduce(matrix_a):
"""
Householder reduce for QR factorization.
:param matrix_a:
:return: matrix_q, matrix_r
"""
# row num: n
# col num: m
n, m = matrix_a.shape
matrix_r = matrix_a
# H_1, H_2, ..., H_n
householder_matrix_list = []
# project each col onto standard basis
for j in range(m):
# Deal with un-reduced sub-matrix.
sub_matrix = matrix_r[j:, j:]
""" Get a_j """
# a_j: column vector j
a = np.reshape(sub_matrix[:, 0],
(len(sub_matrix), 1))
# Check j-col
if not np.nonzero(a)[0].any() or len(a) == 1:
# All rested elements in col_j are zeros.
continue
""" Get v_j = a - |a| e """
# 2-norm of vector a
a_norm_2 = np.int(np.sqrt(np.matmul(a.T, a)))
# standard base e
e = np.zeros_like(a)
e[0] = 1
# v = a - |a| e
v = np.subtract(a, a_norm_2 * e)
""" Get Householder matrix H_j"""
# Household matrix H: I - 2 (vv')/(v'v)
sub_matrix_h = np.identity(len(v)) - 2 * np.matmul(v, v.T) / np.matmul(v.T, v)
# Augment Household matrix
matrix_h = np.identity(n)
matrix_h[j:, j:] = sub_matrix_h
# Mapping current matrix
matrix_r = np.matmul(matrix_h, matrix_r)
# Store Household matrix
householder_matrix_list.append(matrix_h)
""" Reduce R matrix"""
matrix_r = matrix_r[0:m]
""" Compute Q' matrix """
# Compute Q', where Q' = H_n ... H_2 * H_1 * I
matrix_q = np.identity(n)
for household_matrix in householder_matrix_list:
matrix_q = np.matmul(household_matrix, matrix_q)
""" Reduce Q matrix """
matrix_q = np.transpose(matrix_q[0:m])
return matrix_q, matrix_r
def givens_reduce(matrix_a):
r"""
Givens reduce for QR factorization.
:param matrix_a:
:return: matrix_q, matrix,r
Parameters:
-----------
matrix_a: np.ndarray
original matrix to be Givens Reduce factorized.
"""
# row num: n
# col num: m
n, m = matrix_a.shape
matrix_r = matrix_a
# R_1, R_2, ... R_n
givens_matrix_list = []
# Rotation each entry in matrix
for j in range(m): # Col-m
for i in range(j+1, n): # Row-n
if matrix_r[i][j] == 0:
continue
""" Find a and b (current entry) """
a = matrix_r[j][j]
b = matrix_r[i][j]
# Prepare c and s
base = np.sqrt(np.power(a, 2) + np.power(b, 2))
c = np.true_divide(a, base)
s = np.true_divide(b, base)
# Givens trans matrix
matrix_g = np.identity(n)
matrix_g[j][j] = c # Upper Left
matrix_g[i][j] = -s # Lower Left
matrix_g[j][i] = s # Upper Right
matrix_g[i][i] = c # Lower Right
# Rotation
matrix_r = np.matmul(matrix_g, matrix_r)
givens_matrix_list.append(matrix_g)
""" Reduce R matrix """
matrix_r = matrix_r[0: m]
# Compute Q', where Q' = Rn...R2*R1*A
matrix_q = np.identity(n)
for givens_matrix in givens_matrix_list:
matrix_q = np.matmul(givens_matrix, matrix_q)
# Get Q
matrix_q = np.transpose(matrix_q[0: m])
return matrix_q, matrix_r
4.不同语言与平台对QR分解的影响
为探究不同语言与平台对QR分解的影响,分别将Gram-Schmidt QR、Householder QR、Givens QR在Pycharm2021中使用Python重构,具体代码详见附件。
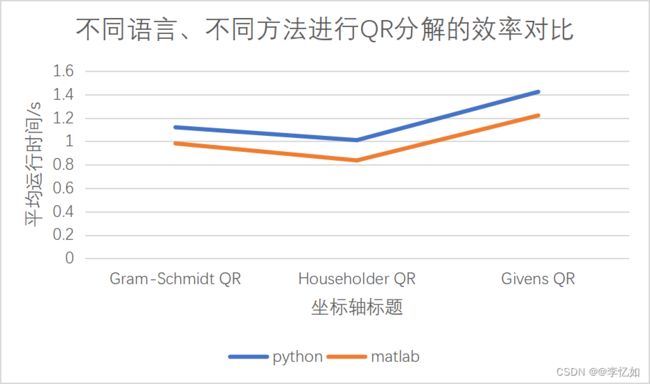
分别使用maatlab与python实现的三种方法对网络数据矩阵D(1000x1000的稠密矩阵)进行QR分解,每个平台的各个方法均进行20次求平均运行时间,数据汇总如表8所示,效果对比如图27所示:
表8 不同语言、不同方法实现QR分解的平均运行时间
图27 不同语言、不同方法进行QR分解的效率对比
分析:由表8与图27可见,在不同方法实现QR分解中,matlab的运行时间均略低于Python,效率较高。
七、实验小结
1.QR分解总结
(1)QR分解常用方法有四种,分别是Gram-Schmidt、Modified Gram-Schmidt、Householder、Givens,各种方法对比简单总结如表9所示:
表9 QR分解的各种实现对比总结
| 方法 |
原理 |
优点 |
缺陷 |
| Gram-Schmidt |
基于正交化定义 |
1.适合小矩阵计算; 2.每次迭代都生成一个正交基,可以随时停止计算 |
1.不适合稀疏矩阵; 2.积累大量舍入误差; 3.循环中必须保存整个矩阵,内存开销大 |
| Householder |
基于迭代镜面反射 |
1.不显式计算Q,只保存若干反射矩阵H,适合仅需要R的任务; 2.最适合稠密矩阵; |
1.迭代过程不产生可用正交基,必须等到全部迭代完成,无法中断。 2.对于稀疏矩阵会产生大量无效计算。 |
| Givens |
基于旋转变换 |
1.最适合稀疏矩阵,仅影响向量的两个分量,不会对零元素做无效操作; |
1.迭代的过程不产生可用的正交基,无法中断 2.不适合稠密矩阵计算,稠密矩阵下的计算量大且需要更多空间; |
(2)通过测试qk与前面列之间的正交性的偏差可以判断不同方法实现QR分解的稳定性,本实验中稳定性由高到低分别是:Householder > Givens > Modified Gram-Schmidt > Gram-Schmidt。
(3)从时间复杂度与稳定性的角度来说,Householder均为最优的QR分解方法,但是在实际工程上,需要根据任务要求和矩阵稠密度灵活分析。如对于稀疏矩阵,使用Givens QR分解的效率最高。
(4)不同语言与平台对于QR分解的效率有一定影响,一般来说,随着矩阵的规模增大,matlab下同方法的QR分解效率会高于Python,在选择的过程中要结合数据与个人熟悉度。
(5)QR分解有多种应用,例如求解线性方程与最小二乘问题,也可以通过QR分解推导相关公式求解其他问题,如求矩阵的逆与伪逆、投影等。
2. 参考资料
1.最优化方法——QR Factorization_显然易证的博客-CSDN博客
2.QR分解的三种实现方法(Gram schmidt等)各自有什么优势和劣势? - 知乎 (zhihu.com)
3.【机器学习】用QR分解求最小二乘法的最优闭式解_LCCFlccf的博客-CSDN博客