Python数据分析之Numpy

前言

NumPy 是使用 Python 进行科学计算的基本包，增加了对大型、多维数组和矩阵的支持，以及在这些数组上操作的大量高级数学函数。NumPy 最初是由 Jim Hugunin 和其他几个开发人员创建的。2005年，Travis Oliphant 结合了另一个同性质的程序库 Numarray 的特色，并加入了其它扩展而开发了 NumPy。NumPy 为开放源代码并且由许多协作者共同维护开发。

它提供了一些很实用的功能

• 功能强大的n维数组对象
• 复杂的（广播）功能
• 集成C/C++和Fortran代码的工具
• 有用的线性代数、傅里叶变换和随机数能力

github 地址： https://github.com/numpy/numpy

文档地址：https://numpy.org/doc/

API 文档地址：https://numpy.org/devdocs/reference/index.html#reference

安装：

pip install numpy

一、数组

NumPy 最重要的一个特点是其 N 维数组对象 ndarray，它是一系列同类型数据的集合，以 下标 0 为开始进行集合中元素的索引。

ndarray 和 python 中普通的数组(列表)的区别有

• NumPy 数组在创建时具有固定的大小，这不像Python 列表，可以动态增长。更改 ndarray 的大小将创建一个新的数组并删除原始数组。
• NumPy 数组中的元素都需要具有相同的数据类型，因此在内存中将具有相同的大小。例外情况：可以有（Python，包括NumPy）对象的数组，从而允许不同大小的元素的数组。
• NumPy数组集成了对大量数据的高级数学和其他类型的操作。通常，与使用Python的内置序列相比，这样的操作执行效率更高，代码也更少。

越来越多的基于科学和数学的基于 python 的软件包正在使用 NumPy 数组；虽然这些输入通常支持 python 序列输入，但它们在处理之前将这些输入转换为 NumPy 数组，并且经常输出 NumPy 数组。换句话说，为了有效地使用当今许多（甚至是大多数）基于Python的科学/数学软件，仅仅知道如何使用Python的内置序列类型是不够的——人们还需要知道如何使用 NumPy 数组。

下面会介绍一些常用函数

1.1 数组创建

import numpy as np

np.array([1, 2, 3, 4, 5, 6])
np.array([[1, 2, 3], [4, 5, 6]], np.int32)

np.zeros((3,4))
np.ones((2,3))
np.empty(2)
np.arange(10, 30, 5)
np.linspace(0, 2, 9)

• array

  创建 1 个数组

  numpy.array(object, dtype=None, *, copy=True, order='K', subok=False, ndmin=0, like=None)
  

  具体文档：https://numpy.org/devdocs/reference/generated/numpy.array.html#numpy.array

• zeros

  创建1个数组，充满0

  numpy.zeros(shape, dtype=float, order='C', *, like=None)
  

  具体文档：https://numpy.org/devdocs/reference/generated/numpy.zeros.html

• ones

  创建1个数组，充满1

  numpy.ones(shape, dtype=None, order='C', *, like=None)
  

  具体文档：https://numpy.org/devdocs/reference/generated/numpy.ones.html

• empty

  创建没有初始化的数组，内容随机

  numpy.empty(shape, dtype=float, order='C', *, like=None)
  

  具体文档：https://numpy.org/devdocs/reference/generated/numpy.empty.html#numpy.empty

• arange

  创建在给定间隔内返回均匀间隔的值数组，不包含结束值，指定间隔

  numpy.arange([start, ]stop, [step, ]dtype=None, *, like=None)
  

  具体文档：https://numpy.org/devdocs/reference/generated/numpy.arange.html

• linspace

  创建在指定间隔内返回均匀间隔的数字数组，包含结束值，指定个数

  numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0)
  

  具体文档：https://numpy.org/devdocs/reference/generated/numpy.linspace.html

1.2 数组属性

数组属性	含义	文档链接
ndarray.ndim	维度数量	https://numpy.org/devdocs/reference/generated/numpy.ndarray.ndim.html
ndarray.shape	数组的维度，对于矩阵，n 行 m 列	https://numpy.org/devdocs/reference/generated/numpy.ndarray.shape.html
ndarray.size	数组元素的总个数，相当于 .shape 中 n*m 的值	https://numpy.org/devdocs/reference/generated/numpy.ndarray.size.html
ndarray.dtype	ndarray 对象的元素类型	https://numpy.org/devdocs/reference/generated/numpy.ndarray.dtype.html
ndarray.itemsize	ndarray 对象中每个元素的大小，以字节为单位	https://numpy.org/devdocs/reference/generated/numpy.ndarray.itemsize.html
ndarray.flags	ndarray 对象的内存信息	https://numpy.org/devdocs/reference/generated/numpy.ndarray.flags.html
ndarray.real	ndarray元素的实部	https://numpy.org/devdocs/reference/generated/numpy.ndarray.real.html
ndarray.imag	ndarray 元素的虚部	https://numpy.org/devdocs/reference/generated/numpy.ndarray.imag.html
ndarray.data	包含实际数组元素的缓冲区，由于一般通过数组的索引获取元素，所以通常不需要使用这个属性。	https://numpy.org/devdocs/reference/generated/numpy.ndarray.data.html
ndarray.strides	在遍历数组时在每个维度中步进的字节元组	https://numpy.org/devdocs/reference/generated/numpy.ndarray.strides.html
ndarray.T	转置数组	https://numpy.org/devdocs/reference/generated/numpy.ndarray.T.html

1.3 数组切片和索引

ndarray 支持索引和切片Slice 访问内部元素，下面会介绍一些简单用法，详细的具体文档可以见：https://numpy.org/devdocs/user/basics.indexing.html#basic-indexing

• 简单索引

  x = np.arange(10)
  x[0]
  x[-2]
  x.shape = (2, 5)
  x[0,3]
  x[1,-1]
  

  

• 切片

  基本切片语法是i:j:k

  • 其中i是起始索引，j是停止索引，k是步进（k != 0）。这将选择具有索引值 i，i+k，…，i+(m-1)*k的m个元素
  • 如果j > N(元素个数)，则为N
  • j也可以省略，默认为N
  • 结果不包含停止索引
  • :k 可以省略，默认步进为1。
  • 如果 i 和 j 是负数，那么实际索引是指N+i, N+j。k如果是负数，那代表逆向

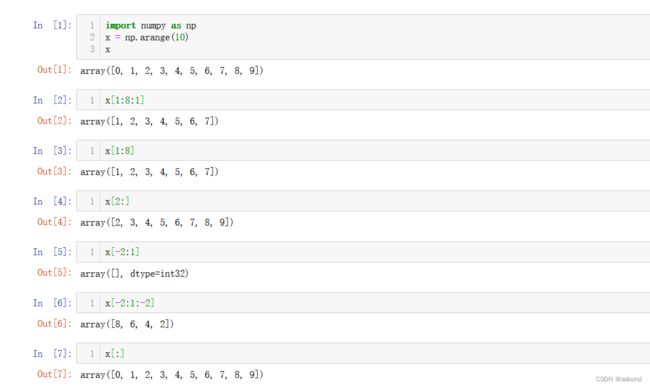
  x = np.arange(10)
  x[1:8:1]
  x[1:8]
  x[2:]
  x[-2:1]
  x[-2:1:-2]
  x[:]
  

• 复合索引和切片

  y=np.arange(35).reshape(5, 7)
  
  y[[0,2,4], [0, 3, 5]]# 二维数组寻找坐标为(0,0) (2,3) (4,5) 三个数
  
  y[1:3, 1:3]# 寻找二维数组第1,2行，再找第1,2列
  
  y[1:3, [1,2]]# 等价上方
   
  y[..., 1:] # ...用于 若干省略的维度保持原样，其他维度保留给定参数的元素
  
  y[y > 5]
  y[(y > 4) & (y < 10)]
  
  y[:, np.newaxis] # 增加轴(维度)
  

1.4 数组广播

广播 这个术语描述了 NumPy 在算术操作过程中如何处理具有不同形状的数组。在一定的约束下，较小的数组在较大的数组上“广播”，从而使它们具有兼容的形状。广播提供了一种向量化数组操作的方法，以便循环发生在C中而不是Python中。它在不制作不必要的情况下复制数据，通常会导致有效的算法实现。然而，在某些情况下，广播是一个坏主意，因为它会导致内存使用不足，从而降低计算速度。

如果两个数组 a 和 b 形状相同，即满足 a.shape == b.shape，那么 a*b 的结果就是 a 与 b 数组对应位相乘。这要求维数相同，且各维度的长度相同。当运算中的 2 个数组的形状不同时，numpy 将自动触发广播机制。

具体文档：https://numpy.org/devdocs/user/basics.broadcasting.html#broadcasting

a = np.array([1, 2, 3, 4])
b = 2
# 会触发广播
a * b 
a + b
a - b
a / b

# 形状不同，报错
y=np.arange(35).reshape(5, 7)
y + a

1.5 数组操作

下面会介绍常用的数组操作函数，具体文档：https://numpy.org/devdocs/reference/routines.array-manipulation.html

• 数组复制

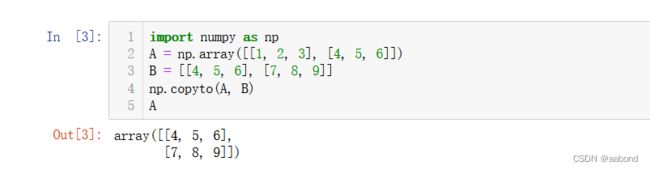
  A = np.array([[1, 2, 3], [4, 5, 6]])
  B = [[4, 5, 6], [7, 8, 9]]
  np.copyto(A, B)
  

• 数组形状修改

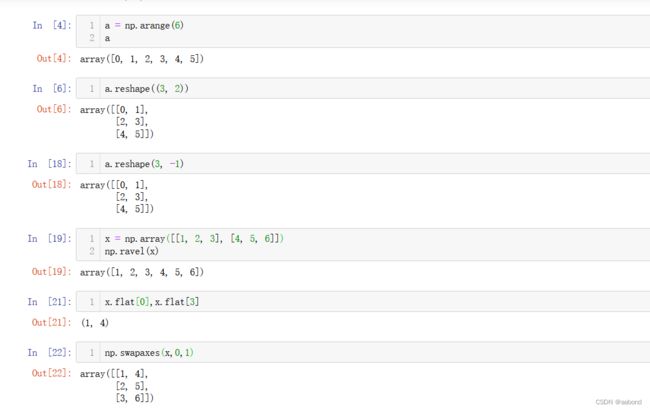
  a = np.arange(6)
  
  a.reshape((3, 2)) # 修改形状
  a.reshape(3， -1) # -1会被推断为2
  
  x = np.array([[1, 2, 3], [4, 5, 6]])
  np.ravel(x) # 转为一维数组
  
  x.flat[0] # 一维迭代器
  x.flat[3]
  
  np.swapaxes(x,0,1) # 交换数组的两个轴
  

• 数组维数扩充

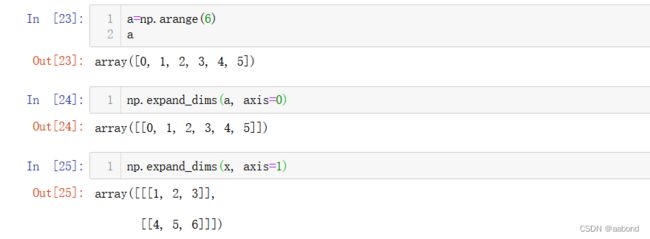
  a=np.arange(6)
  
  np.expand_dims(a, axis=0) # 等价于  x[np.newaxis, :]
  np.expand_dims(x, axis=1) # 等价于  x[:, np.newaxis]
  

• 数组连接和分割

  a = np.array([1, 2, 3])
  b = np.array([4, 5, 6])
  
  np.vstack((a,b)) # 行连接
  np.column_stack((a,b)) # 列拼接
  
  x = np.arange(9)
  np.split(x, 3) #分割
  

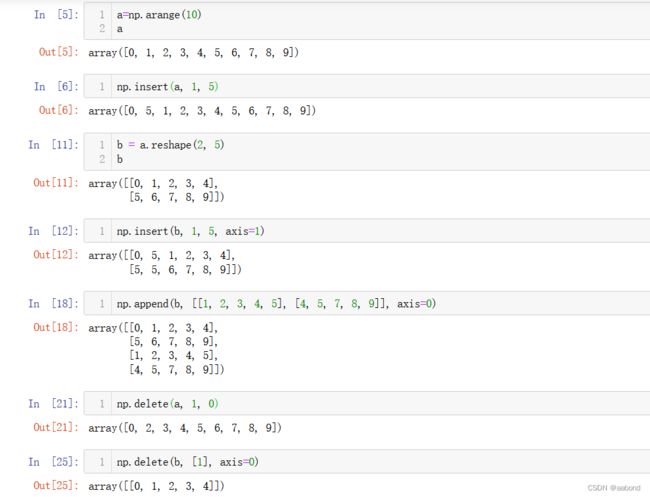
• 数组元素添加与删除

  a=np.arange(10)
  np.insert(a, 1, 5)
  b=a.reshape(2, 5)
  np.insert(b, 1, 5, axis=1)
  
  np.append(b, [[1, 2, 3, 4, 5], [4, 5, 7, 8, 9]], axis=0)
  
  np.delete(a, 1, 0)
  np.delete(b, [1], axis=0)
  

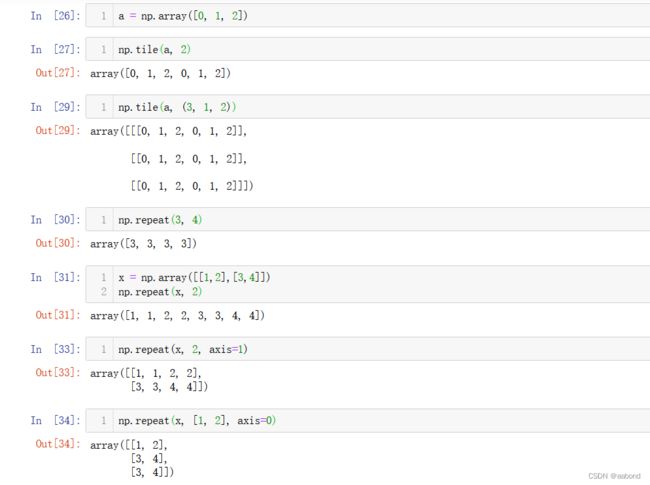
• 数组重复构造

  a = np.array([0, 1, 2])
  
  np.tile(a, 2) 
  np.tile(a, (3, 1, 2))
  
  np.repeat(3, 4)
  
  x = np.array([[1,2],[3,4]])
  
  np.repeat(x, 2)
  np.repeat(x, 2, axis=1)
  np.repeat(x, [1, 2], axis=0)
  

1.6 数组迭代

数组迭代 nditer() 函数, 文档：https://numpy.org/devdocs/reference/generated/numpy.nditer.html#numpy.nditer

class numpy.nditer(op, flags=None, op_flags=None, op_dtypes=None, order='K', casting='safe', op_axes=None, itershape=None, buffersize=0)

下面会介绍常用的数组迭代，具体文档：https://numpy.org/devdocs/reference/arrays.nditer.html#arrays-nditer

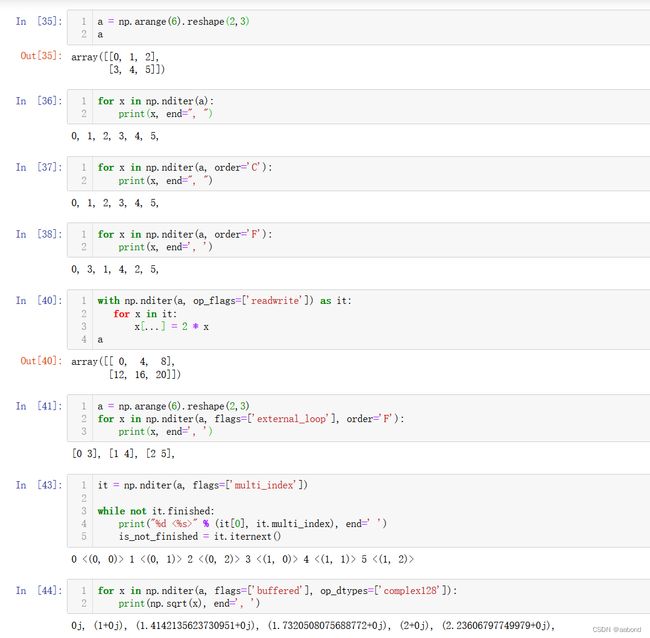
• 简单数组迭代

  a = np.arange(6).reshape(2,3)
  for x in np.nditer(a):
      print(x, end=", ")
   
  for x in np.nditer(a, order='C'):
      print(x, end=", ")
  
  for x in np.nditer(a, order='F'):
      print(x, end=', ')
  
  with np.nditer(a, op_flags=['readwrite']) as it:
     for x in it:
         x[...] = 2 * x
          
  a = np.arange(6).reshape(2,3)   
  for x in np.nditer(a, flags=['external_loop'], order='F'):
      print(x, end=', ')
      
  it = np.nditer(a, flags=['multi_index'])
  while not it.finished:
      print("%d <%s>" % (it[0], it.multi_index), end=' ')
      is_not_finished = it.iternext()
  
  for x in np.nditer(a, flags=['buffered'], op_dtypes=['complex128']):
      print(np.sqrt(x), end=', ')
  

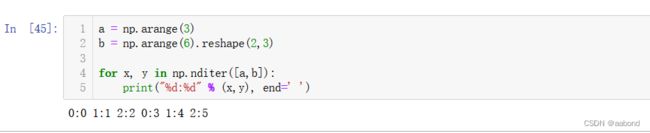
• 广播数组迭代

  a = np.arange(3)
  b = np.arange(6).reshape(2,3)
  
  for x, y in np.nditer([a,b]):
      print("%d:%d" % (x,y), end=' ')
  

二、数学函数

具体文档：https://numpy.org/devdocs/reference/routines.math.html

2.1 三角函数

# 除了sin还有很多三角函数，具体可以查文档
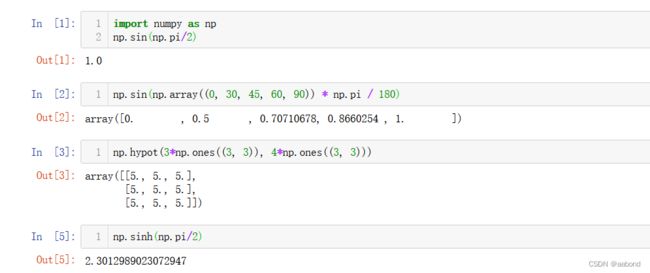
np.sin(np.pi/2)
np.sin(np.array((0, 30, 45, 60, 90)) * np.pi / 180)

# 斜边
np.hypot(3*np.ones((3, 3)), 4*np.ones((3, 3)))

# 双曲函数
np.sinh(np.pi/2)

2.2 运算函数

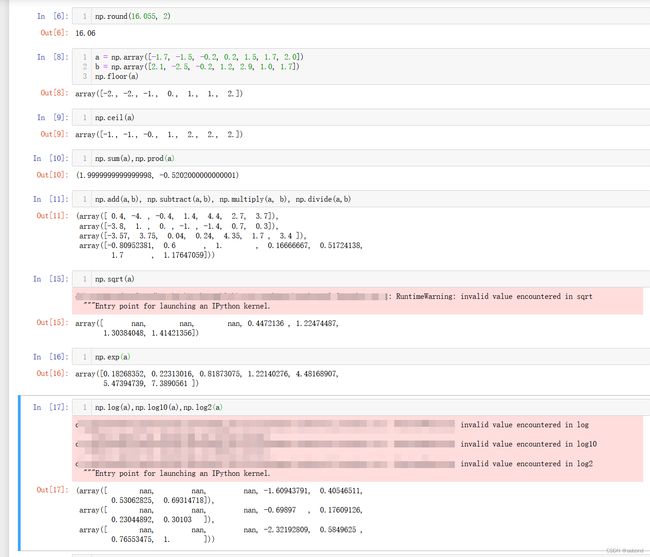
np.round(16.055, 2)# 四舍五入

a = np.array([-1.7, -1.5, -0.2, 0.2, 1.5, 1.7, 2.0])
b = np.array([2.1, -2.5, -0.2, 1.2, 2.9, 1.0, 1.7])
             
np.floor(a) # 向上求整
np.ceil(a)  #向下求整       

np.sum(a) # 求和
np.prod(a)# 求积

#加减乘除
np.add(a,b) 
np.subtract(a,b)
np.multiply(a, b)
np.divide(a,b)

np.sqrt(a)
np.exp(a)
np.log(a)
np.log10(a)
np.log2(a)

2.3 统计函数

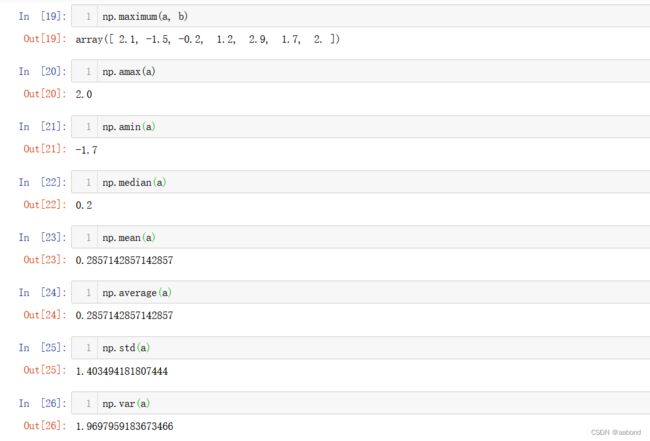
a = np.array([-1.7, -1.5, -0.2, 0.2, 1.5, 1.7, 2.0])
b = np.array([2.1, -2.5, -0.2, 1.2, 2.9, 1.0, 1.7])

np.maximum(a, b) # 两者较大值
np.amax(a) # 最大值
np.amin(a) # 最小值
np.median(a) # 中位数
np.mean(a) # 算术平均值
np.average(a) # 加权平均值
np.std(a) #标准方差
np.var(a) # 方差

2.4 排序及筛选函数

https://numpy.org/devdocs/reference/routines.sort.html

a = np.array([-1.7, -1.5, -0.2, 0.2, 1.5, 1.7, 2.0])
b = np.array([2.1, -2.5, -0.2, 1.2, 2.9, 1.0, 1.7])

np.sort(b) # 排序

np.argsort(b) # 排序元素的索引

np.lexsort((b,a))  # 先通过a排序，相等的元素再通过b排序确定索引，输出索引，稳定排序

np.where(a < b, a, 10 + b)

2.5 线性代数

https://numpy.org/devdocs/reference/routines.linalg.html

a = np.array([[1, 0], [0, 1]])
b = np.array([[4, 1], [2, 2]])

np.dot(a, b) # 点积
np.vdot(a, b) # 向量点积
np.inner(a, b) # 内积
np.matmul(a, b) # 矩阵乘积

np.linalg.det(a) # 计算行列式结果
np.linalg.solve(a, b) # 求解一个线性矩阵方程，或线性标量方程组。
np.linalg.inv(a) # 计算一个矩阵的（乘法）逆。

三、随机数

具体文档：https://numpy.org/devdocs/reference/random/index.html

3.1 简单随机数

https://numpy.org/devdocs/reference/random/legacy.html

https://numpy.org/devdocs/reference/random/generated/numpy.random.rand.html

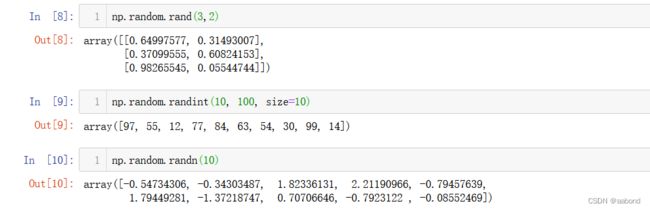
np.random.rand(3,2) # 生成[0, 1)随机浮点数，形状3x2
np.random.randint(10, 100, size=10) # 生成[10,100),10个整数随机数
np.random.randn(10) # 正态分布随机数

3.2 随机排列

np.random.permutation(10)
np.random.permutation([1, 4, 9, 12, 15])

a=np.arrange(10)
np.random.shuffle(a)

3.3 随机分布

np.random.random_sample(10) # [0.0,1.0) 随机浮点数
np.random.standard_cauchy(10) # 柯西分布
np.random.standard_exponential(10) # 指数分布

四、字符串

https://numpy.org/devdocs/reference/routines.char.html

4.1 字符串操作函数

np.char.add(["num", "doc"], ["py", "umentation"])
np.char.capitalize(["python", "numpy"])
np.char.join(['-', '.'], ['ghc', 'osd'])

a = np.array(["That is a mango", "Monkeys eat mangos"])
np.char.replace(a, 'mango', 'banana')
np.char.split(a, ' ')

4.2 字符串比较函数

np.char.equal(['str', '1', 'TRUE'], ['abc', '1', 'FALSE']) 

4.3 字符串信息函数

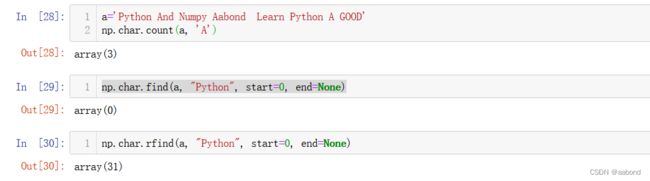
a='Python And Numpy Aabond  Learn Python A GOOD'
np.char.count(a, 'A')
np.char.find(a, "Python", start=0, end=None)
np.char.rfind(a, "Python", start=0, end=None)

五、傅里叶变换

https://numpy.org/devdocs/reference/routines.fft.html

5.1 标准FFT

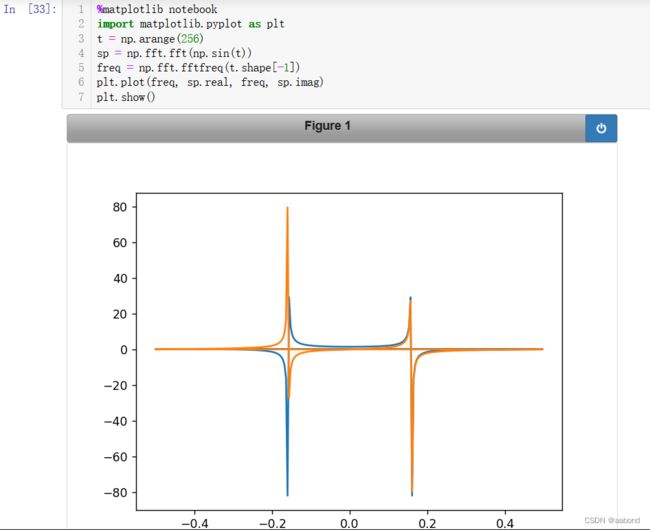
%matplotlib notebook
import matplotlib.pyplot as plt
t = np.arange(256)
sp = np.fft.fft(np.sin(t))
freq = np.fft.fftfreq(t.shape[-1])
plt.plot(freq, sp.real, freq, sp.imag)
plt.show()

5.2 real FFT

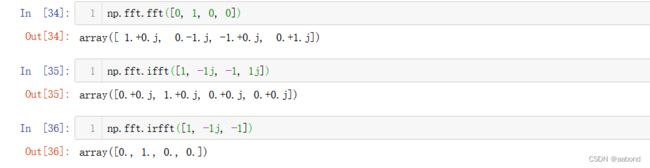
np.fft.fft([0, 1, 0, 0])
np.fft.ifft([1, -1j, -1, 1j])
np.fft.irfft([1, -1j, -1])

5.3 Hermitian FFT

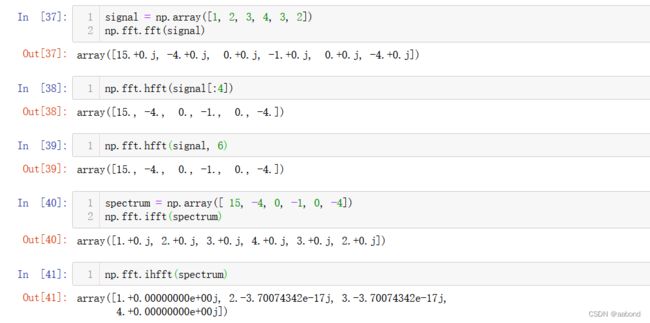
signal = np.array([1, 2, 3, 4, 3, 2])
np.fft.fft(signal)
np.fft.hfft(signal[:4]) 
np.fft.hfft(signal, 6)


spectrum = np.array([ 15, -4, 0, -1, 0, -4])
np.fft.ifft(spectrum)
np.fft.ihfft(spectrum)

六、输入和输出

Numpy 可以读写磁盘上的文本数据或二进制数据。
NumPy 为 ndarray 对象引入了一个简单的文件格式：npy。
npy 文件用于存储重建 ndarray 所需的数据、图形、dtype 和其他信息。
常用的 IO 函数有：

• load() 和 save() 函数是读写文件数组数据的两个主要函数，默认情况下，数组是以未压缩的原始二进制格式保存在扩展名为 .npy 的文件中。
• savez() 函数用于将多个数组写入文件，默认情况下，数组是以未压缩的原始二进制格式保存在扩展名为 .npz 的文件中。
• loadtxt() 和 savetxt() 函数处理正常的文本文件(.txt 等)

具体 IO 函数相关文档可以见：

• https://numpy.org/devdocs/user/basics.io.html

• https://numpy.org/devdocs/reference/routines.io.html

6.1 输入

from io import StringIO
data = u"1, 2, 3\n4, 5, 6"
np.genfromtxt(StringIO(data), delimiter=",")

data = u"\n".join(str(i) for i in range(10))
np.genfromtxt(StringIO(data))
np.genfromtxt(StringIO(data), skip_header=3, skip_footer=5)

c = StringIO("1,0,2\n3,0,4")
np.loadtxt(c, delimiter=',', usecols=(0, 2), unpack=True)

6.2 输出

x = np.arange(10)
np.save('D:\\x.npy', x)

x = y = z = np.arange(0.0,5.0,1.0)
filePath='D:\\test.txt'
np.savetxt(filePath, x, delimiter=',') 
np.savetxt(filePath, (x,y,z))   
np.savetxt(filePath, x, fmt='%1.4e')   

参考

1. https://www.runoob.com/numpy/numpy-tutorial.html