人工智能与数据挖掘复习

一、简答题

1、什么是决策树？

答：决策树是一种分类与回归方法，主要用于分类，决策树模型呈现树形结构，是基于输入特征对实例进行分类的模型。

2、什么是决策表的约简？

答：为了从决策表中抽取得到适应度大的规则，我们需要对决策表进行约简,使得经过约简处理的决策表中的一个记录就代表一.类具有相同规律特性的样本，这样得到的决策规则就具有较高的适应性。

3、简述BP算法的基本思想。

答：1）BP算法的基本思想是，学习过程由信号的正向传播与误差的反向传播两个过程组成。
2）正向传播时，输入样本从输入层传人，经各隐层逐层处理后，传向输出层。若输出层的实际输出与期望的输出不符，则转入误差的反向传播阶段。3）误差反传是将输出误差以某种形式通过隐层向输入层逐层反传，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号即作为修正各单元权值的依据。
4）这种信号正向传播与误差反向传播的各层权值调整过程，是周而复始地进行的。权值不断调整的过程，也就是网络的学习训练过程。此过程一直进行到网络输出的误差减少到可接受的程度，或进行到预先设定的学习次数为止。

4、简述AdaBoost算法。

答：1）Adaboost是一种迭代算法，其核心思想是针对同一个训练集训练不同的分类器（弱分类器），然后把这些弱分类器集合起来，构成一个更强的最终分类器（强分类器）。
2）算法概述
①先通过对N个训练样本的学习得到第一个弱分类器；
②将分错的样本和其他的新数据一起构成一个新的N个的训练样本，通过对这个样本的学习得到第二个弱分类器；
③将1和2都分错了的样本加上其他的新样本构成另一个新的N个的训练样本，通过对这个样本的学习得到第三个弱分类器；
④最终经过提升的强分类器。即某个数据被分为哪一类要由各分类器权值决定。

二、综合题

1、设训练例子集如表所示，请用ID3算法完成其学习过程。

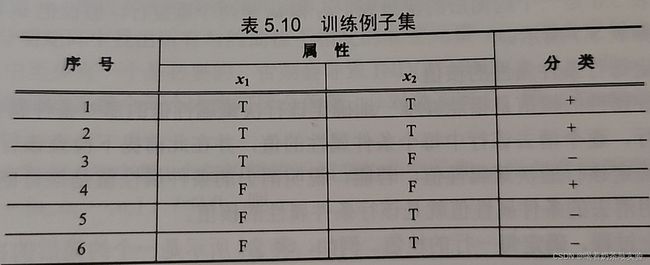
初始化样本集S={S1,S2,…,S6}和属性集X={x1,x2}.
设根节点为(S,X),尽管它包含了所有的训练例子，但却没有包含任何分类信息，因此
具有最大的信息熵。即:
E(S,X)=-Ps(+)log Ps(+)- Ps(-)log Ps(-)
式中
Ps(+)=3/6, Ps(-)=3/6， log2(3/6)=-1
即有
E(S,X)= -(3/6)log 2(3/6) -(3/6)log2(3/6)= 0.5+0.5=1
按照ID3算法，再计算根节点(S, X)关于每个属性的加权信息熵。
先考虑属性x1，对xi1的不同取值:
当x1=T时，有ST={1,2,3}
当x1=F时， 有SF={4,5,6)
其中，ST和SF中的数字均为例子集S中的各个例子的序号，|S|、|ST|和|SF|分别为例子集S、ST和SF的大小且有|S|=6，|ST|=|SF|=3。
由ST可知:
PST(+)=2/3, PST(-)=1/3， log2(2/3)= -0.5850, log2(1/3)=- 1.5850
则有:
E(ST, X)=- PST(+)log2 PST(+)- PST(-)log2 PST(-)
=- (2/3)(-0.5850)- (1/3)(-1.5850)
=-0.9183
再由SF可知:
PSF(+)=I/3, PsS(-)=2/3
E(SF,X)= -PSF(+)log2 PST(+)-PSF(-)log2 PSF(-)
=- (1/3)(-1.5850)- (2/3)(-0.5850)
=0.9183
E((S,X), x1)=( |ST|/|S)E(ST, X)+(|SF|/|S|)E(SF, X)
= (3/6)0.9183+(3/6)0.9183
=0.9183
再考虑属性x2, 对x2的不同取值:
当x2=T时，有S’T={1,2,5,6}
当x2=F时，有S’F={3,4)
其中，S’T和S’F中的数字均为例子集S中的各个例子的序号，|S|、|ST|和|SF|分别为例子集S、ST和SF的大小且有|S|=6，|S’T|=4, |S’F|=2。
由S’T可知:
P’ST(+)=2/4, P’ST(-)=2/4, log(2/4)= -1
则有:
E(S’T,X)=-P’ST(+)log2 P’ST(+) - P’ST(-)log2 P’ST(-)
=-(2/4)(-1)-(2/4)(-1)
=1
再由S’F可知:
P’SF(+)=1/2， P’SF(-)=1/2, log(1/2)=-1
则有:
E(S’F,X)=-(P’SF(+)log2 P’SF(+)-PSF(-)log2 P’SF(-)
=-(1/2)(-1)-(1/2)(-1)
E((S,X),x2)=( |ST|/|S)E(ST, X)+(|SF|/|S|)E(SF, X)
=(4/6)*1+(2/6)*1=1
据此，可得到各属性的信息增益分别为
G((S,X)x1)=E(S, X)- E((S, X), x)= 1-0.9183=0.0817
G((S,X)x2)= E(S, X)-E((S, X),x2)=1-1=0 I
显然，x1的信息熵最大，因此应该对x1进行扩展。扩展x1后生成的部分决策树如下:

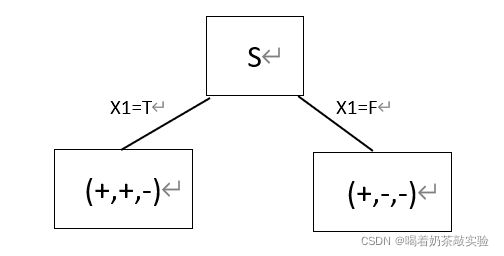
从属性集中删去已扩展的属性x1,得新的属性集集X1={x2}。由于现在属性集中的属性仅剩x1，故扩展x1,得到最终的完整决策树，如下图所示:

2、假设w(0)=0.2, w2(0)=0.4, θ (0)-0.3, η=0.4,请用单层感知器完成逻辑或运算的学习过程

根据“与”运算的逻辑关系，可将问题转换为:
输入向量: X1=[0, 0, 1, 1] ，X2=[0, 1,0, 1]
输出向量: Y=[0, 0, 0, 1]

为减少算法的迭代次数，我们对初始连接权值和阈值取值如下:
W1(0)=0.5, w2(0)=0.7, θ (0)=0.6

并取增益因子η=0.4。算法的学习过程如下:
设感知器的两个输入为x1(0)=0和x2(0)=0,其期望输出为d(0)=0,实际输出为:
y(0)=f(w1(0) x1(0)+ w2(0) x2(0)- θ (0))
=f(0.50+0.70-0.6=f(-0.6)=0

实际输出与期望输出相同，不需要调节权值，再取下一组输入: x1(0)=0 和x2(0)=1,其期望输出为d(0)=0,实际输出为:
y(0)=(w1(0)x1(0)+ w2(0) x2(0)- θ(0)
=f(0.50+0.71-0.6)=f(0.1)=1

实际输出与期望输出不同，需要调节权值，其调整如下:
θ(1)= θ(0)+ η(d(0)- y(0))(-1)=0.6+0.4(0-1)(-1)=1
wl(1)=w1(0)+ η(d(0)- y(0))x1(0)=0.5+0.4(0-1)0=0.5
w2(1)=w2(0)+ η(d(0)- y(0))x2(0)= 0.7+0.4(0-1)1=0.3

取下一组输入: xl(1)=1 和x2(1)=0，其期望输出为d()=0,实际输出为:
y(1)=f(w1(1)xI(1)+w2(1)x2(1)- θ(1))
=f(0.51+0.30-1)=f(-0.51)=0

实际输出与期望输出相同，不需要调节权值，再取下一组输入: x1(1)=1 和x2(1)=1,其期望输出为d()=I,实际输出为:
y(1)-f(w1(1)x1(1)+ w2()x2(1)- θ(1))
=f(0.51+0.31-1)=f(-0.2)=0

实际输出与期望输出不同，需要调节权值，其调整如下:
θ(2)=θ(1)+ η(d(1)- y(1))(-1)=1+0.4*(1-0)(-1)=0.6
wl(2)=w1(1)+ η(d(1)- y(1))x1(1)=0.5+0.4*(1-0)1=0.9
w2(2)=w2(1)+ η(d(1)-y(1)x2(1)=0.3+0.4*(1-0)1=0.7

取下一组输入: x1(2)=0 和x2(2)=0,其期望输出为d(2)=0,实际输出为:
y(2)=f(0.90+0.70-0.6)=f(-0.6)=0

实际输出与期望输出相同，不需要调节权值，再取下一组输入: x1(2)=0 和x2(2)=1,其期望输出为d(2)=0,实际输出为:
y(2)=f(0.90+0.71-0.6)=f(0.1)=1

实际输出与期望输出不同，需要调节权值，其调整如下:
θ(3)= θ(2)+ η(d(2)- y(2))(-1)=0.6+0.4*(0-1)(-1)=1
w1(3)=w1(2)+ η(d(2)- y(2))x1(2)=0.9+0.4*(0-1)0=0.9
w2(3)=w2(2)+ η(d(2)-y(2))x2(2)=0.7+0.4*(0-1)1=0.3

实际上，由上一章关于与运算的阈值条件可知，此时的阅值和连接权值以满足结束条件,算法可以结束。可以检验如下:
对输入:“00” ,有y=f(0.90+0.30-1)-f(-1)=0
对输入:“01” ,有y=f(0.90+0.30.1-1)-18=f(0.7)-0
对输入:“10” ,有y=f(0.91+0.30-1)=f(-0.1)=0
对输入:“11” ,有y=f(0.91+0.31-1)=f(0.2)=0

三、填空题

1、基本遗传操作分为____、_____、____。

基本遗传操作分为选择、交叉、变异。

2、遗传算法中采用_____法产生下一代种群。

遗传算法中采用迭代法产生下一代种群

3、信息熵是对信息源整体_____性的度量，而信息增益描述的是_____。

信息熵是对信息源整体不确定性的度量，而信息增益描述的是一个属性区分数据样本的能力。

4、Adaboost 算法中， 某弱学习器ht的权重at的计算公式是 (错误率为εt)

5、是否具备启发性信息是区别盲目搜索和智能搜索的关键。用来估计节点的重要性函数称为估价函数。估价函数由两部分组成，分别为_____、_____。

估价函数由两部分组成，分别为g(n)、h(n)。

6、BP 网络的学习过程是由工作信号的_____组成的。

BP 网络的学习过程是由工作信号的正向传播和误差的反向传播组成的。