东北大学2020级数据科学基础（Matlab）非计算机类大作业——Titanic幸存者分析

首先感谢大佬@自由散漫惯
kaggle经典题–“泰坦尼克号”–0.8275准确率–东北大学20级python大作业开源（附详细解法与全部代码以及实验报告）

本文matlab代码：
本文matlab代码

提取码：kx6m

1 题目

本次数据科学Matlab大作业需要自选数据、问题，利用课程所学，进行数据探索性分析，应用聚类、分类等方法，完成数据分析实战，并进行相应的可视化展示。

作为非计算机类的学习者，作业与计算机类的不同要求为：

• 数据集中记录数不低于300，属性不低于4个，不允许使用教学中用过、实验课用过的数据集；
• 可以使用Matlab自带的相关分析工具箱

在本次作业中，笔者选择了Kaggle数据科学平台上的入门项目——Titanic作为作业题目。

---

Titanic是数据科学平台kaggle上的一个入门竞赛，它为参赛者给出了test.csv、train.csv、gender_submission.csv三份数据文件，其中包含了泰坦尼克号上1309位旅客的性别、年龄、座舱等级等各种相关信息（测试集418条，训练集891条），有些数据存在空缺，有些数据存在异常，此外还存在数据不规范等问题，参赛者需要对数据进行合理的处理，可以运用描述性统计、数据可视化、分类、聚类等方法对数据进行基本的分析，再通过机器学习、决策树等方法对泰坦尼克事故的幸存者进行预测。

2 任务分析

• Titanic竞赛的最终目标是给出泰坦尼克事故的幸存者预测
• 为了实现预测，需要用到机器学习、决策树等构建模型手段
• 为了构建模型，需要对所给出数据进行探索性（包括描述性、相关性）等基本的分析，尝试提前特征，并且需要用Matlab进行数据可视化
• 为了数据分析，需要对数据预处理，填充或删除空缺值、排除异常值、规范化不同的属性值，以Matlab的方法
• 在利用Matlab数据分析前，还要将数据导入至Matlab中

3 实验过程

3.1 数据预处理

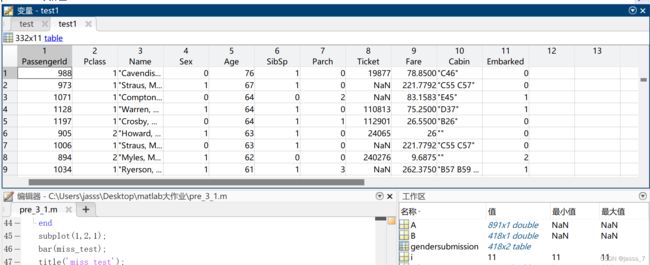
3.1.1 观察数据

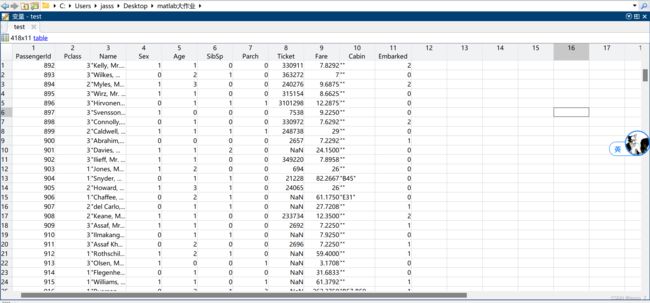
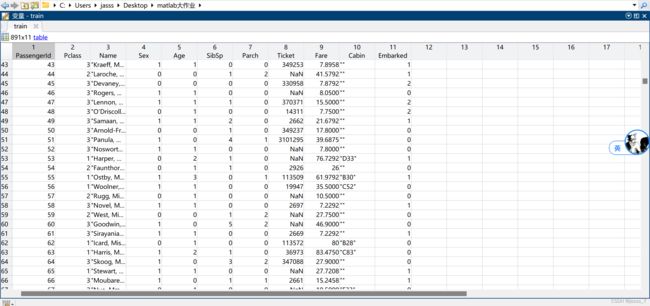
首先依次观察test.csv、train.csv、gender_submission.csv三份数据集。

可以看到，test.csv是测试集，而train.csv属性与test.csv基本一致，只是多了一个Survived（是否幸存）属性，gender_submission.csv则是test.csv测试集的答案。数据集总体含有以下属性：

---

PassengerId：乘客编号

Pclass：座舱等级

Name：乘客姓名

Sex：乘客性别

Age：乘客年龄

SibSp：兄弟姐妹和配偶数量

Parch：父母与子女数量

Ticket：票号

Fare：票价

Cabin：座位号

Embarked：出发港口

---

通过观察可以获得一些简单的分析思路：

• PassengerId一项只是唯一标识，与幸存与否无关；

• Name一项作为字符串，格式工整，家族姓氏在一定程度上可以体现身份地位，与幸存有着潜在关系；

• Sex一项值为Female与male，需要进一步规范为0、1；

• Ticket一项格式较乱，但票号中可以体现的的信息也应该可以从Fare、Cabin、Embarked等属性中体现出来，分析时可以与Passenger一样作为唯一标识放在一边；

• Cabin一项空缺值较多，怀疑隐含着有无座位的信息，与幸存有着潜在关系，分析时可以按是否空缺进行区分；

• Embarked一项与Sex一样，需要进一步规范为0、1、2；

• 其余项对于分析基本合适，但注意到有些属性值相较于其他属性值更大（如Fare），在建模时可能会成为主导影响因素进而影响模型准确率，需要进一步进行归一化处理；

3.1.2 建立MAT文件

.mat文件的方便之处在于，它可以连同数据的变量名一同保存下来，并且不需要控制数据的存储格式，matlab会自动保存并区分我们所储存的内容。利用load和save指令可以实现对.mat文件的读写。

为了更方便地在Matlab中对数据进行操作，且便于直接点击执行m文件，笔者先把.csv文件转换成.mat文件。

这样一来可以通过以下命令简单而快速导入数据：

load('test.mat');
load('train.mat');
load('gender.mat');

3.1.3 特征规范化

由3.1.1初步分析可知，Sex、Embarked两个属性作为离散型字符特征，为了便于进一步分析，需要规范化处理。对于Sex，令female对应0，male对应1；对于Embarked，令S对应0，C对应1，Q对应2。

代码如下：

% 特征规范化
A=test{:,4};
A=string(A);
A(A=='female')=0;
A(A=='male')=1;
A=double(A);
test.Sex=A;

A=train{:,5};
A=string(A);
A(A=='female')=0;
A(A=='male')=1;
A=double(A);
train.Sex=A;

A=test{:,11};
A=string(A);
A(A=='S')=0;
A(A=='C')=1;
A(A=='Q')=2;
A=double(A);
test.Embarked=A;

A=train{:,12};
A=string(A);
A(A=='S')=0;
A(A=='C')=1;
A(A=='Q')=2;
A=double(A);
train.Embarked=A;

3.1.4 填充空缺值

预处理数据时，应该对测试集、训练集应用相同的处理方法，但不应该合并之后一起处理。

训练模型时一定不能把测试集的信息代入，要假设测试集不存在

因此笔者并没有把训练集、测试集合并起来寻找统计数据。

a 寻找空缺值

先寻找测试集、训练集中的空缺值：

% 先去除train中Survived属性
train(:,2)=[];
miss_test=[];
for i=1:size(test,2)
    miss_test=[miss_test sum(ismissing(test(:,i)))];
end
subplot(1,2,1);
bar(miss_test);
title('miss test');
set(gca,'xTicklabel',{'PassengerId','Pclass','Name','Sex','Age','SibSp','Parch','Ticket','Fare','Cabin','Embarked'}); 
miss_train=[];
for i=1:size(train,2)
    miss_train=[miss_train sum(ismissing(train(:,i)))];
end
subplot(1,2,2);
bar(miss_train,'FaceColor','#EDB120');
title('miss train');
set(gca,'xTicklabel',{'PassengerId','Pclass','Name','Sex','Age','SibSp','Parch','Ticket','Fare','Cabin','Embarked'}); 

得到如下两个柱形图：

可以看到测试集、训练集中空缺值都主要集中在Age、Ticket两个属性中，除此以外Fare中有1个缺失值，Embarked中有2个缺失值。

在3.1.1观察数据时我们还看到Cabin属性中有很多""值，Matlab的ismissing()函数并没有把它算成空缺值，而笔者分析时也考虑到是否存在有座无座与幸存与否的潜在关系，故空缺值处理时不对Cabin处理。

对于Age属性，采取先分类再预测填充策略，对于Fare属性，采取中位数直接填充策略；对于Ticket属性，暂时放置不管；对于Embarked这样的离散型变量，采取众数填充。

中位数相较平均数，受噪点数据影响更小

众数是出现次数最多的数，在一定程度上反映了离散型变量的均值

b 先分类再填充

提取测试集中的Age属性非空记录，准备训练分类模型：

i KNN分类填充

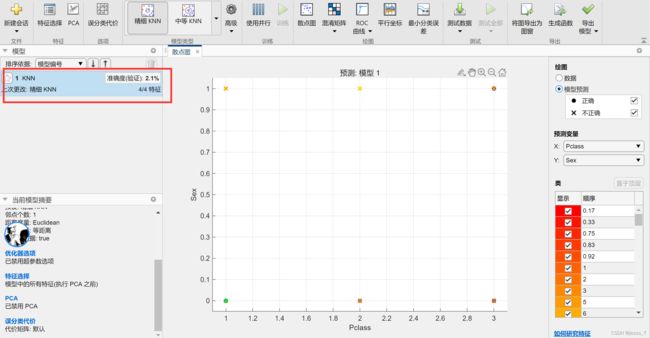
通过matlab自带的分类学习器，选择交叉验证K折数为5，因变量Age，自变量Pclass、Sex、SibSp、Parch：

四个特征时，KNN准确率过低，选择Pclass、Sex两个特征再次KNN，结果依然不理想：

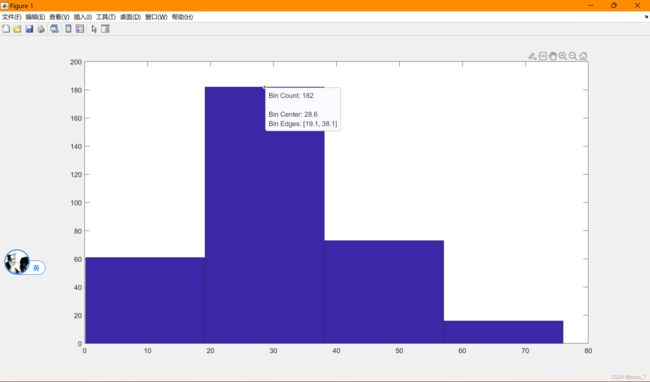
考虑到Age属性值范围可能从0~100，但此处的训练集只有332个，难以获得高准确度的预测模型，选择先把Age属性分成4类。

hist(test.Age,4);

边界分别是下界-19.1-38.1-57-上界

通过以下代码把test中的Age分为四类：

test15=test{:,5};
for i=1:size(test15,1)
    if ismissing(test15(i,1))
        continue
    elseif test15(i,1)<19.1
        test15(i,1)=0;
    elseif test15(i,1)<38.1
        test15(i,1)=1;
    elseif test15(i,1)<57
        test15(i,1)=2;
    else
        test15(i,1)=3;
    end
end
test15=array2table(test15);
test(:,5)=test15;

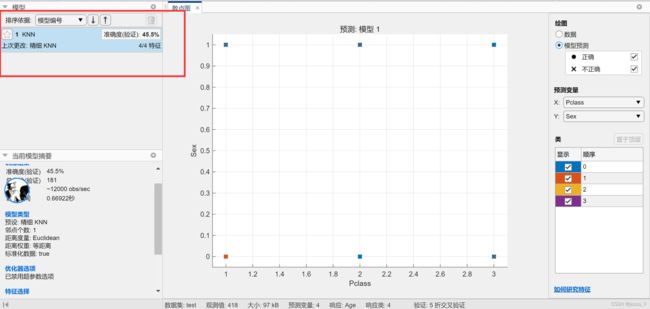
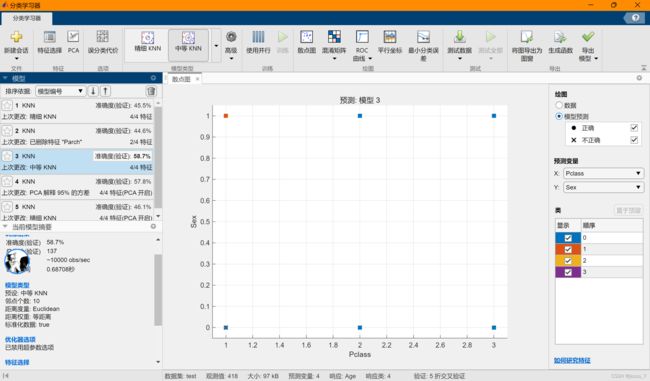
再次KNN，四特征，准确度上升至45%：

尝试修改特征、改变K值，多次KNN：

最终得到一个准确度58.7%的模型，用其填充Age空缺值。

代码如下：

Age=test{:,5};
Parch=test{:,7};
Pclass=test{:,2};
Sex=test{:,4};
SibSp=test{:,6};
filltest_Age=table(Age,Parch,Pclass,Sex,SibSp);
c=[1];
for i=1:size(filltest_Age,1)
    if ismissing(filltest_Age(i,1))
        b=filltest_Age(i,2:5);
        c=AgeKNN.predictFcn(b) ;
        c=array2table(c);
        filltest_Age(i,1)=c;
    end
end
test.Age=filltest_Age{:,1}

填充效果：

ii 中位数填充

实际上，在Age缺失值填充的过程中可以看到，利用KNN分类的效果并不是特别理想。因此，对于只有一个缺失值的Fare属性，笔者改为采取中位数填充方法。

代码：

Fare=test.Fare;
Fare(ismissing(Fare))=median(Fare);
test.Fare=Fare;

iii 众数填充

在train中，Embarked是一个有缺失值的离散型变量，笔者选择以众数填充，代码如下：

Embarked=train.Embarked;
Embarked(ismissing(Embarked))=mode(Embarked);
train.Embarked=Embarked;

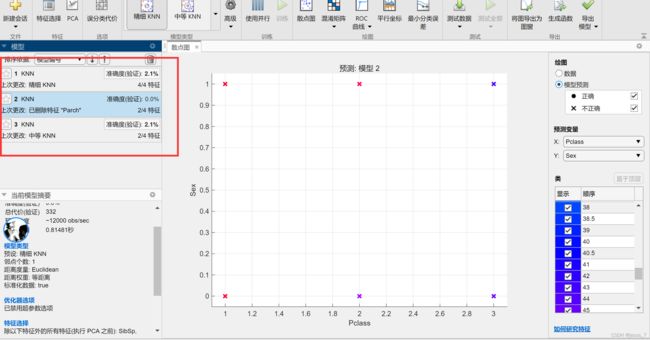
iiii SVM分类填充

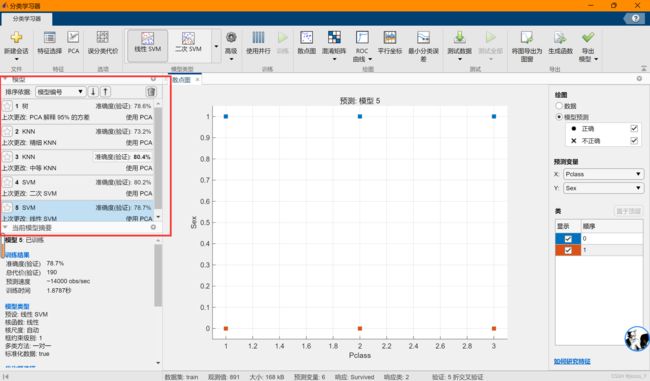
train中的Age同样用模型训练再填充，方法类似，先把Age分为四类然后训练模型，但此处选择了二次SVM模型，开启PCA后准确度达到58.3%，略好于KNN：

用相同方法导出模型并进行填充，代码：

Age=train{:,5};
Parch=train{:,7};
Pclass=train{:,2};
Sex=train{:,4};
SibSp=train{:,6};filltest_Age=table(Age,Parch,Pclass,Sex,SibSp);
c=[1];
for i=1:size(filltest_Age,1)
    if ismissing(filltest_Age(i,1))
            b=filltest_Age(i,2:5);
            c=AgeSVM.predictFcn(b) ;
            c=array2table(c);
            filltest_Age(i,1)=c;    
    end
end
train.Age=filltest_Age{:,1};

填充效果：

3.2 探索性分析

3.2.1 柱形图比较各属性下存活与死亡数据

先根据Survived把各记录区分开。（此处探索性分析使用的数据集为预处理后但留有Survived属性的训练集）

绘制Pclass、Sex、Age、SibSp、Parch、Fare、Cabin、Embarked共八个属性的柱形图，代码如下：

subplot(2,4,1);
x=[sum(figure_train1{:,1}==1),sum(figure_train1{:,1}==2),sum(figure_train1{:,1}==3)];y=[sum(figure_train2{:,1}==1),sum(figure_train2{:,1}==2),sum(figure_train2{:,1}==3)];
A=[x;y];
barh(A);
legend('1','2','3');
set(gca,'yTicklabel',{'survived','no survived'});
title('Pclass');
subplot(2,4,2);
x=[sum(figure_train1{:,3}==0),sum(figure_train1{:,3}==1)];y=[sum(figure_train2{:,3}==0),sum(figure_train2{:,3}==1)];
A=[x;y];
barh(A);
legend('female','male');
set(gca,'yTicklabel',{'survived','no survived'});
title('Sex');
subplot(2,4,3);
x=figure_train1.SibSp;
y=figure_train2.SibSp;histogram(x);
hold on;
histogram(y);
legend('survived','no survived');
title('SibSp');
subplot(2,4,4);
x=figure_train1.Parch;
y=figure_train2.Parch;
histogram(x);
hold on;
histogram(y);
legend('survived','no survived');
title('Parch');
subplot(2,4,5);
x=figure_train1.Fare;
y=figure_train2.Fare;
histogram(x);
hold on;
histogram(y);
legend('survived','no survived');
title('Fare');
subplot(2,4,6);
x=[sum(figure_train1{:,9}==0),sum(figure_train1{:,9}==1),sum(figure_train1{:,9}==2)];y=[sum(figure_train2{:,9}==0),sum(figure_train2{:,9}==1),sum(figure_train2{:,9}==2)];
A=[x;y];
barh(A);
legend('S','C','Q');
set(gca,'yTicklabel',{'survived','no survived'});
title('Embarked');
subplot(2,4,7);
x=figure_train1.Age;
y=figure_train2.Age;
histogram(x);
hold on;
histogram(y);
legend('survived','no survived');
set(gca,'xTicklabel',{'--19.1','19.1-38.1','38.1-57','57--'});
title('Age');
subplot(2,4,8);
x=[sum(figure_train1{:,8}==''),342-sum(figure_train1{:,8}=='')];y=[sum(figure_train2{:,8}==''),549-sum(figure_train2{:,8}=='')];
A=[x;y];
barh(A);
legend('no Cabin','Cabin');
set(gca,'yTicklabel',{'survived','no survived'});
title('Cabin');

结果：

综合以上8幅图，可以看到，一等座幸存比例大于其他座位；女性幸存者数量多于男性幸存者，并且比例也大于男性；有家人（SibSp、Parch不等于0）的人，幸存的比例大于无家人的人，可能是亲人互帮互助使生存率提升；Cabin有值的人，幸存比例也比Cabin无值的人高。

3.2.2 箱线图探索离群值

对Fare、Age两项数据范围比较大的属性进行离群值探索。

代码：

% 创建新图窗
figuresubplot(1,2,1);
boxplot(train.Fare,train.Survived);
title('Fare');
set(gca,'xTicklabel',{'no survived','survived'});
load('train.mat');
subplot(1,2,2);
boxplot(train.Age,train.Survived);
title('Age');
set(gca,'xTicklabel',{'no survived','survived'});

结果：

可以看到，Fare中大部分数值都在100以下，但幸存者的票价总体上略高于未幸存者票价；Age中，大部分年龄都在30岁上下，幸存者年龄总体上比未幸存者小一点，可见在危机关头大多数人还是把希望托付给了年轻人。

3.2.3 相关系数矩阵

利用corr()函数，求不同变量之间的相关系数，并以矩阵的形式呈现出来。代码：

train6=train1Copy{:,:};
co=corr(train6);

结果：

在相关系数的角度，变量间关系并不是非常明显。

3.3 预测幸存者

3.3.1 模型训练

由此前的分析，可知，Pclass、Sex、Age、SibSp、Parch、Cabin与Survived之间可能有着较突出的关联关系。为了预测幸存者，笔者选择使用以上变量，利用Matlab分类工具箱进行幸存者预测。

得到5个模型，其中最好的准确度80.4%来自开启PCA的中等KNN。

ROC曲线，很接近左上角。

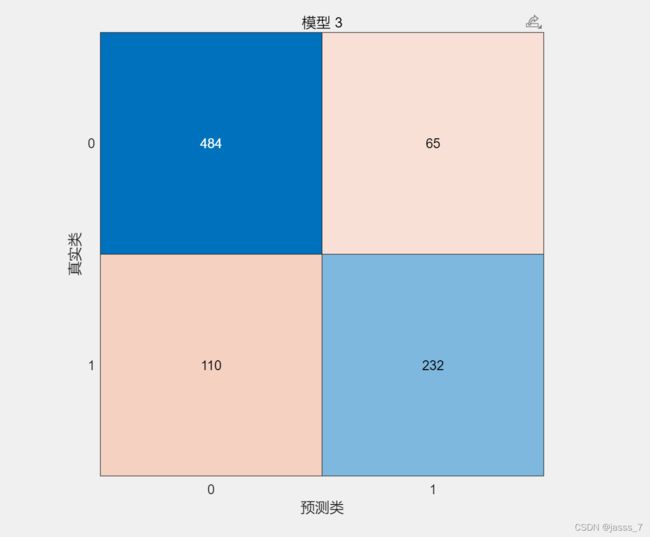
混淆矩阵。

3.3.2 测试模型

将模型导出，利用如下代码，计算模型在测试集上的准确度：

result=FinalKNN.predictFcn(test001);
accuracy = sum(result==gendersubmission{:,2})/size(gendersubmission,1);

结果准确度为：

效果并不是很理想。

预测结果并不理想，暂不打算就此提交至Kaggle平台，回顾分析过程，自我反思还有很大的提升空间。

4 结果反思

回顾整个数据分析结果，最后模型预测准确度并不理想，个人认为在数据预处理、模型训练上还有很大的不足是导致结果的主要原因。虽然不同数据集训练的结果不同，但本次分析中处理后的数据用KNN、SVM模型训练，准确度都没能达到85%，并且最后在测试集上的结果也只有不到65%。个人总结具体原因可能有以下几点：

• 数据预处理不够合理。在处理数据时，没必要直接开始用模型训练来填充空缺值，因为模型训练存在很大的偶然性，用中位数直接填充或许会更加稳定合理。
• 模型训练方法局限。本次分析中只用到了KNN、SVM、决策树等分类工具，事实上还可以尝试聚类、神经网络等工具，并且Matlab也提供了相应的APP，在改进分析时，可以考虑用不同的方法，相互比较、从中择优预测。
• 模型调参不足。本次分析中无论是KNN、SVM亦或是决策树，基本都一直在使用默认参数，并且验证方法也一直是K折为5的交叉验证，如果恰当地调整参数，期望的准确度理应会上升。
• 探索性分析不够深入。在探索性分析这一方面，对于数据的挖掘不够深入，始终是在数据的表面徘徊，并且没有做好主成分分析等特征工程，致使后来的模型训练其实并不是很合理。
• 对Matlab编程技术掌握得还不够熟练。在本次分析中，切实感受到自己Matlab知识的贫瘠，尤其是关于Table型数据的读取、编辑以及矢量化编程。在数据可视化方面，也常常感受到自己的编程没法实现自己大脑中的设计。
• （讲真我再做分析肯定用python不用matlab，matlab报个错我去谷歌都未必知道是怎么回事，而且matlab画的图美化起来与python相比太费劲了）
• 花的时间太少了。实际上这个大作业在1月5号上午11点之前一直处于新建文件夹的状态，11点开写然后到凌晨1点写完、录制完讲解视频。如果能多花点时间，肯定能把分析和代码优化得更好。（新的一年希望自己拖延症好转）

写在最后

最后必须感谢z老师。总算让我完成了一点matlab的学习，虽然很可能短期内都不会想去用matlab，但多多少少给我留下了一点印记。

这个学期也是难忘的。假如说这学期学matlab有什么心得，那一定是，遇到matlab大佬，一定要好好珍惜！