超分之RCAN

这篇文章是2018年的ECCV，作者主要是为了介绍注意力机制在超分领域的应用以及基于注意力机制的这个SR网络——Residual Channel Attention Networks(后文简称RCAN)。RCAN是一种基于Residual In Residual(后文简称RIR)结构的深度网络，他利用残差网络的特性来加深网络；RIR由多个Residual Groups(后文简称RG)组成，每个RG由多个Residual Channel Attention Blocks(后文简称RCAB)组成；而每个RCAB是一个含有通道注意力机制Channel Attention(后文简称CA)的残差块。

参考列表：
①RCAN-Image Super-Resolution Using Very DeepResidual Channel Attention Networks
②Image Super-Resolution Using Very Deep Residual Channel Attention Networks
③RCAN源码

Abstract

①想要提升SR的表现力，最直接的方法就是增加模型复杂度，模型复杂度的增加可以通过增加网络宽度实现，比如EDSR就是比较知名的非常宽的SR网络；此外，增加网络深度也是一个重要的方向，为了避免网络深度带来的梯度消失现象，RCAN利用何凯明提出的残差网络来加深SR模型的深度。
②之前的SR方法对于feature map不同通道是一样处理的，但作者提出不同通道它所含的特征信息是不同的，有的通道的feature map含有重要信息，而有的通道所含的可能是无效甚至是不利于图像重建的feature map。
基于上述2点，作者提出了RCAN超分模型，它具有非常深的网络结构以及包含通道注意力机制的特性，我们简要描述下RCAN的网络结构：

1. RCAN模型由低层特征提取、高层特征提取、上采样层、重建层组成，其中高层特征提取和SRResNet、SRDenseNet、EDSR一样使用残差网络或者稠密网络来做的，但是不同于后者，RCAN中使用了RIR结构，其通过Long skip connection将低层特征信息和高层特征信息进行相加；而RIR由多个RG组成，RG由多个具有注意力机制的残差块组成，而在RG中会继续将低层信息和高层信息通过Short skip connection相加。
2. 在每个残差块中加入了通道注意力机制，旨在对于不同通道的feature map赋予不同的缩减因子，因此整个feature map中不同通道的特征图对输出的影响是不同的。
3. RIR结构使用skip connection将低层和高层特征信息相结合，使得网络深度可以加深，从而就可以获取更多的高层特征信息。
4. 在当时RCAN取得了SOTA的表现力！

1 Introduction

RCAN的提出基于前人算法体现的2大问题：

1. EDSR发表的时候取得了SOTA的表现力，证明了网络深度对超分的影响。但作者指出，像EDSR一样只是单纯堆积残差块来构建越来越深的SR网络并不会有更好的表现力。
2. 之前的SR算法对于不同通道的处理都是相同的，而其实每一个通道包含着不同重要程度的特征信息，比如有的通道的特征信息对重建HR有着重要意义，而有的通道信息不仅没用还会损害$LR\to HR$。

因此作者推出RCAN，其于EDSR一样利用残差块以及skip connection来加深网络。但是不同于较宽的EDSR或较深的MDSR的简单堆积，RCAN使用RIR结构，其使用RG结构和Long Skip Connection(以下简称LSC)来加深网络从而可以提取$LR$层级更多的低层特征和高层特征信息，其中就包括低频信息和高频信息(低频信息是一些平坦大块的区域，高频信息是边缘、纹理、区域等细节信息)。每个RG模块才使用多个具有注意力机制的残差块(RCAB)和Short Skip Connection(SSC)，而每个残差块内部有short-cut(短程连接，也可以算skip connection)来进行残差连接。关于每个残差块内部的注意力，对不同通道就不能同等视之，作者在RCAN中引入通道注意力机制(CA)，自适应学习一个通道权重来给予不同的注意力。CA的引入增加了SR网络的灵活性以及使得SR网络更加关心有用的通道特征。
RCAN的表现力如下：

Note：

1. EDSR中虽说是简单堆积残差块，但也是用了一条skip connection的。

总结一下这篇文章的贡献点：

1. 提出$RIR\to RG\to RCAB$以及$LSC\to SSC\to short-cut$的结构来加深SR网络。
2. 在RCAB中引入通道注意力机制来使得网络注意有用信息更多的通道。
3. 结合以上两点推出完整的RCAN超分模型，其包括低层特征提取、高层特征提取、上采样层、重建层。

2 Related Work

略

3 Residual Channel Attention Network (RCAN)

这一节开始介绍RCAN的整体网络模型，其中：

1. 3.1节介绍整体过程。
2. 由于除了高层特征提取以外，其余结构都和EDSR等经典模型差不多，因此作者会重点讲解RCAN特别的高层特征提取部分。3.2、3.3、3.4小节分别介绍RIR、CA、RCAB模块的内部实现。

3.1 Network Architecture

RCAN网络结构如下：

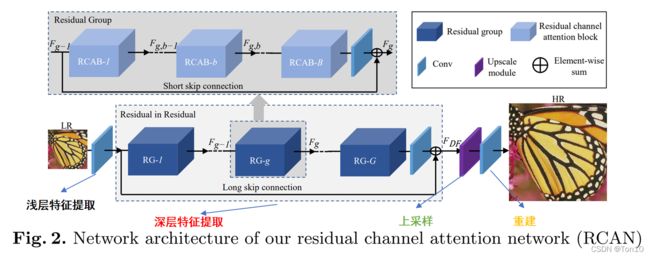
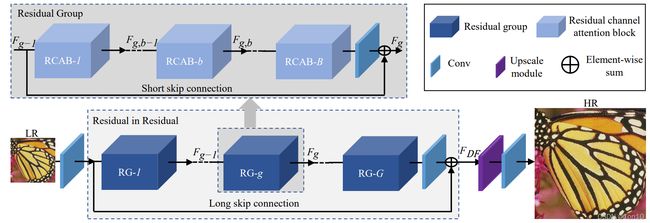
整个RCAN模型包括4部分：
①浅(低)层特征提取。
②RIR深(高)层特征提取。
③上采样层。
④重建层。

Note：

1. 整体结构和SRDenseNet、SRResNet、EDSR等类似，唯一不同的就是他们之间关于高层特征提取的做法不同。
2. 接下来我们分别展开讲述上述4个部分。

①浅层特征提取：
RCAN使用简单一层卷积层来提取输入$I^{LR}$的浅层特征信息(Shallow Feature)，设$H_{SF}(\cdot )$表示浅层特征提取算子，$F_0$为该层输出feature map，则表达式为：
$$F_0=H_{SF}(I_{LR})\text{\hspace{1em}(1)}$$

②RIR深层特征提取：
深层特征(Deep Feature)提取使用非常深的RIR结构，其包含多个RG块，其算子用$H_{RIR}(\cdot )$表示，作者指出目前来说RIR已经达到了最大的深度以及最大的感受野，具体表达式为：
$$F_{DF}=H_{RIR}(F_0)\text{\hspace{1em}(1)}$$

③上采样层：
SR中的上采样大致有3种方式，比如反卷积(本质也是卷积，或者叫转置卷积)、最近邻上采样、亚像素卷积(ESPCN)等。设$F_{UP}(\cdot )$表示上采样算子，具体表达式为：
$$F_{UP}=H_{UP}(F_{DF})\text{\hspace{1em}(3)}$$在实验中，作者采用ESPCN提出的亚像素卷积层。

④重建层：
重建层简单使用一层卷积层来将上采样输出$F_{UP}$进行下一步的调整和优化，用$H_{REC}(\cdot )$算子来表示该过程，具体表达式为：
$$I_{SR}=H_{REC}(F_{UP})=H_{RCAN}(I_{LR})\text{\hspace{1em}(4)}$$Note：

1. $H_{RCAN}(\cdot )$为整个RCAN网络的表达。

RCAN使用$L1$损失函数，设$I_{HR}$为Ground Truth，$\Theta$为RCAN的参数，则RCAN优化的目标为：
$$L(\Theta )=\frac{1}{N}\sum _{i=1}^N||H_{RCAN}(I_{LR}^i)-I_{HR}^i||.\text{\hspace{1em}(5)}$$

由于不同算法主要在深层特征提取不同，因此作者接下来只具体展开介绍RIR深层特征提取部分。

3.2 Residual in Residual (RIR)

在RIR结构中，包含了$G$个RG块以及1个LSC来连接2个阶段的特征信息；每个RG块包含$B$个RCAB块以及1个SSC来连接2个阶段的特征信息，此外RCAB是一个基础的残差块结合通道注意力并使用short-cut连接输入和输出2个阶段特征信息的块。

RCAN基于RIR这样的残差结构，来训练出一个深度超过400层的SR网络并取得了不错的表现力！接下来我们介绍下RIR结构：

之前EDSR使用残差块堆叠的方式取得了不错的表现力，但是如果继续加深深度，则SR的训练就会变得十分困难且无法提升表现力，因此RCAN改变结构，在RIR中使用RG块来取代EDSR中的残差块从而在SR中进一步加深网络深度。

我们用表达式来描述上述过程，设$H_g(\cdot )$表示第$g$个RG块的映射，$F_{g-1}、F_g$表示第$g$个RG块的输入feature map和输出feature map：
$$F_g=H_g(F_{g-1})=H_g(H_{g-1}(\cdots H_1(F_0)\cdots )).\text{\hspace{1em}(6)}$$
作者指出若简单的堆叠RG块，会使得表现力无法提升，因此增加了LSC来稳定训练以及使得较深的网络结构得以实现。增加了LSC之后，整个RIR结构得表达式如下：
$$F_{DF}=F_0+W_{LSC}{F}_G=F_0+W_{LSC}{H}_g(H_{g-1}(\cdots H_1(F_0)\cdots )).\text{\hspace{1em}(7)}$$其中，$W_{LSC}$是RIR尾巴处的一层卷积层参数，这里省略bias。

小结下LSC的功能：

1. 使得低层级的特征信息可以跨越层级和高层级信息融合，使得最终获得的特征信息更加全面、丰富，为SR的重建提供更多帮助。
2. 使得网络可具备一定深度的能力，通过梯度反传让网络可以去学习到残差信息。

---

为了进一步融合更多不同层级的信息，在每个RG内部也同样使用skip connection——SSC，即文中的identity-based skip connection。接下来我们来介绍下RG模块：

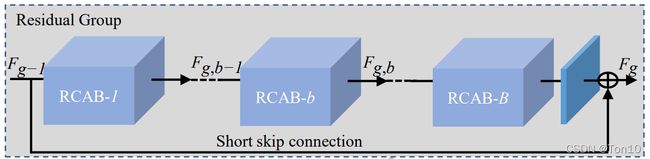
RG模块由$B$个通道注意力残差块RCAB组成，并使用SSC连接RG块内的低层信息和高层信息，设$F_{g,b-1}、F_{g,b}$表示第$g$个RG块中第$b$个RCAB块的输入与输出，$H_{g,b}(\cdot )$为第$g$个RG块内第$b$个RCAB块的映射，则RG的数学表达式为：
$$F_{g,b}=H_{g,b}(F_{g,b-1})=H_{g,b}(H_{g,b-1}(\cdots H_{g,1}(F_{g-1})\cdots ))\text{\hspace{1em}(8)}$$
和LSC一样，我们在RG内部添加SSC，故整个RG模块的数学表达式为：
$$F_g=F_{g-1}+W_g{F}_{g,B}=F_{g-1}+W_g{H}_{g,B}(H_{g,B-1}(\cdots H_{g,1}(F_{g-1})\cdots ))\text{\hspace{1em}(9)}$$其中$W_g$为RG块内最后一个卷积层的参数，这里省略bias。

SSC和LSC的功能是一样的，正是有了LSC和SSC，才使得更多不同层级的特征信息得以融合，也使得网络的深度得以变深，让更多的残差信息得以学习。

3.3 Channel Attention (CA)

之前的SR算法对于不同通道的feature map都同等看待，不加区分的用相同的操作去做，但其实不同通道所包含的特征信息是不同的，故需要引入注意力机制，让网络去注意多通道中对重建更有用的信息，这就是多通道注意力机制(CA)，CA它实际考虑的是不同通道之间的关系，即不同通道之间根据自身的特性受到不同程度的偏好。

产生不同通道注意力需要一个反应不同通道重要程度的常数权重$w$以及将权重和通道特征信息相结合的机制。
①：前者作者通过全局平均池化实现，就是将不同通道的feature map映射成一个常数，具体来看：
我们设输入feature map为：$X=[x_1,\cdots ,x_c,\cdots ,x_C]$，其中$c\in \{0,\cdots C-1\}$是第$c$个输入通道数，$C$为输入通道总数。池化的结果为$z\in {\mathbb{R}}^C$，即一个一维张量，长度为$C$，该过程的数学表达式为：
$$z_c=H_{GP}(x_c)=\frac{1}{H\times W}\sum _{i=1}^H\sum _{j=1}^W{x}_c(i,j).\text{\hspace{1em}(10)}$$
Note：

1. $H、W$为输入feature map的高和宽，$H_{GP}(\cdot )$为全局平均池化。
2. CA是channel-wise，即通道级的，故运算是按不同通道来做的。

②后者通过CNN门控来实现，门控机制如RNN中的门一样，使用激活函数sigmoid/tanh作为开关，以相乘的方式和输入相互结合，具体数学表达如下：
$$s=f(W_U\delta (W_{D}z)).\text{\hspace{1em}(11)}$$
Note：

1. $\delta (\cdot )、f(\cdot )$分别表示ReLU激活函数和sigmoid门。
2. $W_D$是将全局平均池化的结果进行通道下采样，通过卷积的方式使得输出通道变为原来的$\frac{1}{r}$；$W_U$是进行通道上采样，通过卷积的方式将输出通道变为输入通道数的$r$倍，这里$r$不是SR缩放因子，实验中取$r=16$。
3. 注意力权重是一个可以学习的张量。

最后我们按不同通道将权值和feature map进行相乘结合
$$\widehat{x_c}=s_c\cdot x_c.\text{\hspace{1em}(12)}$$其中$x_c$为第$c$个通道的feature map。

---

综上所述，CA模块的具体结构如下：

CA使用PyTorch可表示为：

class CALayer(nn.Module):
    def __init__(self, channel, reduction=16):     
        super(CALayer, self).__init__()
        # global average pooling: feature --> point
        self.avg_pool = nn.AdaptiveAvgPool2d(1)  # 自适应全局平均池化层
        # feature channel downscale and upscale --> channel weight
        self.conv_du = nn.Sequential(
                nn.Conv2d(channel, channel // reduction, 1, padding=0, bias=True),
                nn.ReLU(inplace=True),
                nn.Conv2d(channel // reduction, channel, 1, padding=0, bias=True),
                nn.Sigmoid()
        )

    def forward(self, x):
        y = self.avg_pool(x)
        y = self.conv_du(y)
        return x * y  # 最后返回不同重要性通道的feature map

x就是 HxWxC 通道  y是权重 
y权重通过上面方式求出，然后 和x求乘积
使得重要通道权重更大，不重要通道权重减小

3.4 Residual Channel Attention Block (RCAB)

这一节是在RG的残差块中引入通道注意力机制，从而得到一个RCAB块，其网络结构如下所示：

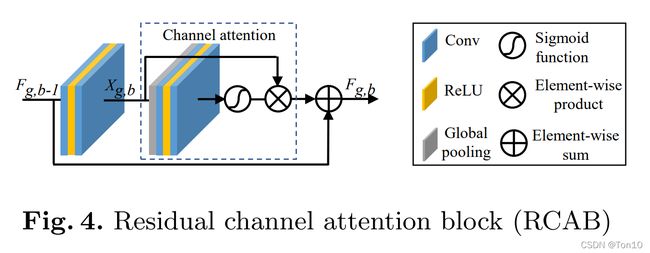
如上图所示，作者在基本残差块的残差$X_{g,b}$上再串接一个CA，最后再用short-cut进行连接，具体表达式为：
$$F_{g,b}=F_{g,b-1}+R_{g,b}(X_{g,b})\cdot X_{g,b}.\text{\hspace{1em}(13)}$$其中$R_{g,b}(\cdot )$表示第$g$个RG中第$b$个RCAB中CA的映射关系，$X_{g,b}$是残差特征信息，它通过$conv2d\to ReLU\to conv2d$的简单CNN层输出得到，具体如下：

$$X_{g,b}=W_{g,b}^2\delta (W_{g,b}^1{F}_{g,b-1}).\text{\hspace{1em}(14)}$$其中$W_{g,b}^1、W_{g,b}^2$是卷积层的参数，这里省略bias。

---

RCAB使用PyTorch可表示为：

class RCAB(nn.Module):
    def __init__(
        self, conv, n_feat, kernel_size, reduction, bias=True, bn=False, act=nn.ReLU(True), res_scale=1):
        super(RCAB, self).__init__()
        modules_body = []
        for i in range(2):
            modules_body.append(conv(n_feat, n_feat, kernel_size, bias=bias))
            if bn: modules_body.append(nn.BatchNorm2d(n_feat))
            if i == 0: modules_body.append(act)
        modules_body.append(CALayer(n_feat, reduction))
        self.body = nn.Sequential(*modules_body)
        self.res_scale = res_scale

    def forward(self, x):
        res = self.body(x)
        # res = self.body(x).mul(self.res_scale)
        res += x
        return res

Note：

1. 其中self.res_scale表示了Inception-Residual这篇论文的Residual Scaling技巧，用于稳定深度较深的CNN训练，他是注意力机制的特殊情况。

---

还有个有趣的地方，EDSR这篇论文推出了EDSR和MDSR两个超分结构，其中EDSR使用了0.1的residual scaling，MDSR没有使用。而residual scaling使用的位置和CA一摸一样，因此EDSR和MDSR可以看成是RCAN的一种特殊情况，具体来说，当RCAN中RCAB使用$R_{g,b}(\cdot )=0.1$，那么RCAB模块就相当于EDSR中的残差块；若RCAB中不适用CA或者$R_{g,b}=0$，那么RCAB模块就相当于MDSR的残差块。因此RCAB相对于EDSR和MDSR的残差块更加灵活，它可以利用不同通道的特征信息以及它们之间的关系(获取不同权重)来灵活调整块地输出，让网络除了缩减feature map的值来稳定训练，从而获得更加宽的网络(因为滤波器越多，输出通道越多，网络越不稳定，而网络的宽度是由滤波器的个数决定的)之外，还可以挑选对重建更有用的信息且适当丢弃不好的特征信息，从而提升模型的表现力。

Note：

1. 从RCAB和EDSR/MDSR的残差块对比来看，CA除了引入注意力机制以外也具有residual scaling的作用，即增加网络训练稳定性，并且为拓宽网络宽度提供了基础。
2. 关于EDSR和residual scaling可以参考我的另一篇超分之EDSR。

4 Experiments

4.1 Settings

1. 使用DIV2K数据集训练；使用Set5、Set14、B100、Urban100、Manga109数据集做测试。
2. 在Y通道上使用PSNR/SSIM作为图像质量客观评价指标。
3. 训练使用self-ensemble，即一些增强操作：水平翻转、旋转90°、旋转180°、旋转270°。
4. Batch=16。
5. 输入patch为$48\times 48$。
6. 使用Adam优化。
7. 初始化学习率设置为$10^{-4}$，每隔$2\times 10^5$个iterations，学习率减半。
8. $G=10,B=20$。
9. 除了CA使用$1\times 1$卷积外，其余均使用$3\times 3$卷积核。
10. 除了CA使用$\frac{C}{r}、r$($r=16$)的通道以外，其余均使用$C=64$。
11. 上采样层使用亚像素卷积层。

4.2 Effects of RIR and CA

关于RIR和CA的作用，作者通过去掉LSC和SSC以及CA在Set5测试集上测试，其中残差块个数$B=200$。
实验结果如下所示：

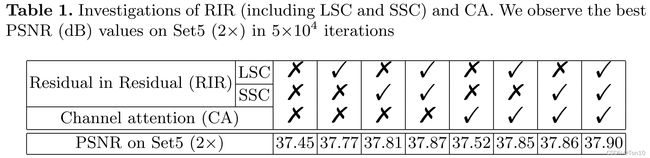
1. 从实验结果来看，当LSC/SSC均去掉的话，不管CA是否存在，PSNR都会处于一个比较低的值，比如37.45和37.52。因此光是简单堆积残差块，而不设置skip connection的话，对于深度网络下的SR是很难训练，无法取得高表现的，也就是说无skip connection下，在$B=200$这样只靠残差块堆积产生的深度是很难训练的，换句话说，同样数据集下只能训练出一个较浅的网络，但是较浅的网络其模型表现力往往是不够的。
2. 添加了LSC和SSC之后的表现力要优于所有情况，一来说明了跨层信息融合是有助于SR重建的；二来说明了RIR结构有助于SR在深度网络中的应用，是可以学到东西的，RIR在skip connection存在下可以驾驭更深的网络，比如37.45和37.87以及37.52和37.90。
3. 添加了CA之后的实验要比任意不添加实验获取的表现要更好，说明了通道注意力机制对超分的重要性。

4.3 Results with Bicubic Degradation Model

本小节作者将RCAN和其余11种超分算法相比较，实验结果如下：

1. 从实验结果来看，RCAN取得了最佳的表现，除此之外，随着缩放倍率越大，RCAN和EDSR之间的差距越大。
2. EDSR的参数量大概在43M，而我们的RCAN在16M，RCAN在较轻量的基础上还拥有更高的表现力。
3. 这张表获得最有用的结论：更深的网络深度和通道注意力机制对SR表现力都有促进作用。
4. RCAN+表示RCAN使用了自集成方法。

可视化结果如下：

4.4 Results with Blur-downscale (BD) Degradation Model

实验结果以及可视化如下：

4.5 Object Recognition Performance

超分通常作为高级计算机视觉任务，比如目标识别的预处理部分，作者比较了RCAN于几种SR算法在目标识别领域上的性能对比，实验结果如下：

从结果来看，RCAN使得目标识别得到了最低的Top-1、Top-5 error。

4.6 Model Size Analyses

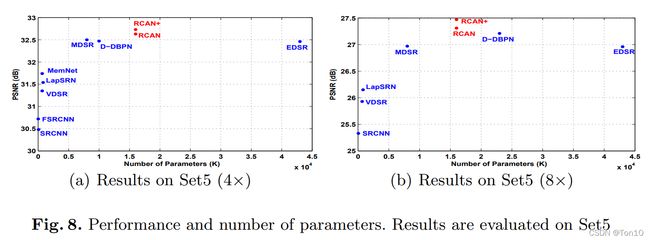
上图是RCAN与几种SR算法在模型参数和表现力上的统计图，从图中可知：

1. RCAN与RCAN+的模型参数比EDSR要少很多，但是表现力更高！
2. RCAN与RCAN+在模型复杂度和表现力上实现了较好的trade-off。
3. 深度网络可能比宽度网络对超分对表现力的提升更好。

5 Conclusions

1. 论文提出了一种基于RIR结构且引入了通道注意力机制的深度超分网络——RCAN，其包含浅层特征提取、深层特征提取、上采样层以及重建层。其中深层特征提取就是采用RIR结构，其包含$G$个RG块并采用LSC连接不同层级的特征信息；而每个RG块又包含$B$个RCAB块并采用SSC连接RG内不同层级的特征信息；每个RCAB块使用short-cut残差块以及通道注意力CA模块。实验证明，RCAN具有驾驭深度非常深的SR网络的能力。
2. LSC和SSC可以直接将低层得到的低频的信息直接跨层和高层的特征信息融合，并迫使网络集中学习残差信息获取更丰富的高层特征信息，比如物体区域等。当然Skip connection的存在也是可训练出深度网络存在的一个重要原因。
3. 文中最重要的是提出了通道注意力机制。通过对不同通道施加不同的权重来提供不同重要程度的特征信息，因为不同通道的特征信息是有好有坏的，有的对图像的超分具有提升作用，而有的会损坏重建的质量，因此我们通过这个权重来让网络更加注重那些有用的特征信息，从而更好的提升表现力。