数学建模——区分“拟合、插值、多元线性回归、逻辑回归、逐步回归、最小二乘法”等概念【概念篇】【全文5200字】
文章目录
- 一、总关系图
- 二、插值 和 拟合 的区分
- 三、拟合 和 回归 的区分
- 四、多元线性回归 和 多元逐步回归 的区分
- 五、多元线性回归 和 逻辑回归 的区分
- 六、回归分析 与 最小二乘法 的区分
- 七、总结:
- 八、参考附录:
笔者尽量用简洁的语言来描述。
数学建模系列文章——总结篇:《数模美一国一退役选手的经验分享[2021纪念版]》.
一、总关系图
解释说明:
①拟合、插值和逼近是数值分析的三大基础工具。它们的区别在于:
<1>拟合是已知样本点列,从整体上靠近它们;
<2>插值是已知样本点列并且完全经过点列;
<3>逼近是已知实际函数曲线,或者样本点列,通过逼近使得构造的理论函数曲线无限靠近它们。
②拟合就是把平面上一系列的样本点,用一条光滑的曲线连接起来。因为这条曲线有无数种可能,从而有各种拟合方法。拟合的曲线一般可以用函数表示,根据这个函数的不同有不同的拟合名字。
③按照 自变量 的个数的多少,可分为一元回归分析和多元回归分析。
④按照 自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
⑤逻辑回归的因变量的值 一般为“是”或“否”【即 “0” 或 “1”】,但自变量可以包括很多。自变量既可以是连续的,也可以是分类的。
⑥另外,logistic回归(逻辑回归)的因变量可以是二分类的,也可以是多分类的,但是 二分类的更为常用,多类可以使用softmax方法进行处理。
⑦逐步回归的基本思想是:将变量一个一个引入,引入的条件是:其偏回归平方和检验是显著的。同时,每引入一个新变量后,对已入选回归模型的老变量逐个进行检验,将经检验认为不显著的变量删除,以保证所得自变量子集中每一个变量都是显著的。此过程经过若干步 直到 不能再引入新变量为止。这时回归模型中所有变量对因变量都是显著的。
⑧另外,在实战中,可以使用 逐步回归函数 stepwiselm()【基于:matlab】可以从一个模型出发,尝试增加或者减少一项(自变量),从而改进结果,直到无法改进为止。
注:根据 因变量 的个数的多少,可分为简单回归分析和多重回归分析。这在上面那张关系图中未画出来。
二、插值 和 拟合 的区分
①从几何意义上将,拟合是给定了空间中的一些样本点,找到一个 已知形式但未知参数 的 连续曲线/曲面 来最大限度地逼近这些点;而插值是找到一个(或几个分片光滑的) 连续曲线/曲面 来穿过这些点。因此拟合可以用于外推预测。而差值一般用于求解差值空间里面的未知函数值,一般不能外推。
补充:与拟合相关的一个概念是回归分析,它更多地关注 统计推断 的问题。例如:分析并拟合一组带有随机误差数据的曲线中的不确定性。 拟合曲线 可以用于 数据可视化 或 推断没有数据可用的函数值 ,并总结两个或多个变量之间的关系。外推 是指使用超出观测数据范围的拟合曲线,并且存在一定程度的不确定性。
三、拟合 和 回归 的区分
①回归是一种数据分析方法。
②拟合是一种数据建模方法。
③拟合侧重于调整曲线的参数,使得与数据相符。而回归重在研究两个变量或多个变量之间的关系。它可以用拟合的手法来研究两个变量的关系,以及出现的误差。
四、多元线性回归 和 多元逐步回归 的区分
①逐步回归只是回归过程采用的其中一种方法而已。
②多元线性回归可以和非线性回归相区分,也就是解释变量和被解释变量之间建立的回归方程,如果是线性的,则是线性回归,否则是非线性回归。
③多元逐步回归是回归分析建模的一种,举个例子来说,现在有一个因变量A,建模的时候可能的解释变量有5个,分别是B1、B2、B3、B4和B5,但是搞不清楚5个变量哪些是解释变量,哪些是干扰变量,所以就想到把变量采用不同的方法 放 到模型中去进行回归建模。而 放 变量的方法具体有可分为Enter法、Forward前进法、Backward后退法、Stepwise逐步回归法等。当然最终建立的模型可以是线性的,也可以是非线性的。
④另外,补充一下:SPSS里线性回归过程,操作的步骤:Analyze——Regression——Linear,回归过程解释变量的方法 默认 的是Enter法,如果是逐步回归则要换成Stepwise。当然因为选的是线性回归过程,只能建立出线性回归模型。
五、多元线性回归 和 逻辑回归 的区分
①logistic回归是一种广义线性回归(generalized linear model),因此与 多重线性回归分析 有很多相同之处。
注:根据 因变量 的个数的多少,可分为简单回归分析和多重回归分析。这在上面那张关系图中未画出来。
②它们的模型形式基本上相同,都具有 w’x+b,其中w和b是待求参数,其 区别在于 他们的因变量不同,多重线性回归 直接 将w‘x+b作为因变量,即 y =w’x+b。而logistic回归则通过函数L将w’x+b对应一个隐状态 p,p = L(w’x+b)。然后根据 p 与 1-p 的大小决定因变量的7值。如果 L 是 logistic函数,就是logistic回归,如果L是多项式函数就是多项式回归。
六、回归分析 与 最小二乘法 的区分
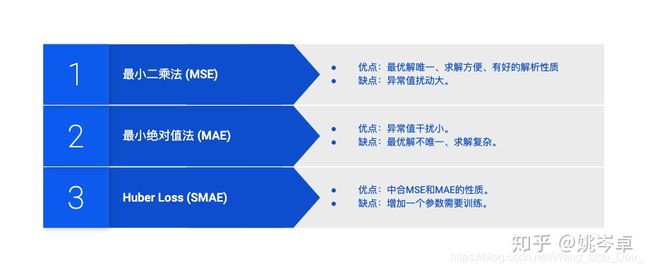
“ 最小二乘法 ” 只是 回归分析 中的一种方法,同样地,和最小二乘法相对应的还有:最小绝对值法 等【如下图所示,详细内容见 参考附录③】。
七、总结:
我从多种角度【总览角度、对比角度等】去区分这些专业名词的概念,但仍然还是有疏漏的地方我相信。
最后,我没有详细地阐述其原理,如要了解详细的原理,可以看看文章最后的参考附录吧。
八、参考附录:
[1] 《拟合(Curve fitting)与回归(Regression analysis)》【通过这篇文章,你可以领悟到 更原始 的概念】
链接: https://blog.csdn.net/xu_fengyu/article/details/91402376.
[2] 《多元线性回归、逐步回归、逻辑回归的总结》
链接: https://blog.csdn.net/ddxygq/article/details/101351479.
[3] 《在进行线性回归时,为什么最小二乘法是最优方法?》:主要看 姚岑卓 的回答,很棒。
链接: https://www.zhihu.com/question/24095027.
[4] 《数学建模之数据拟合(3):最小二乘法》:看完这个视频,你可以 更友好地理解 最小二乘法
链接: https://www.bilibili.com/video/BV1q741177US?from=search&seid=12421359005753840035.
[5] 《[学习笔记]多元线性回归分析——理解篇》
链接: https://blog.csdn.net/weixin_46059493/article/details/106225974.
[6] 《回归分析》:来自百度百科
链接: https://baike.baidu.com/item/%E5%9B%9E%E5%BD%92%E5%88%86%E6%9E%90/2625498?fr=aladdin.
数学建模系列文章——总结篇:《数模美一国一退役选手的经验分享[2021纪念版]》.
⭐️ ⭐️