matlab - 3 自由度的机械臂

实验说明

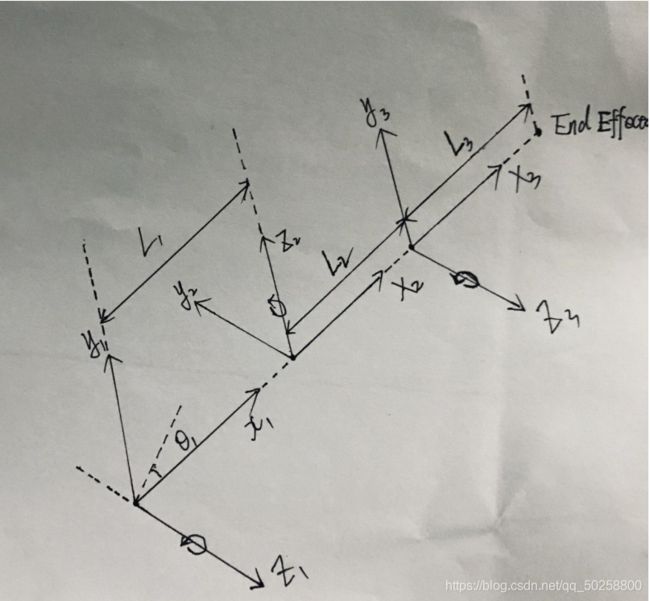
• 你的控制器应该能够控制一个 3 自由度的机械臂到达给定的目的地。
• 代码有注释。
• 可视化

matlab环境

matlab版本：2017a
安装的工具包：机器人工具箱，即robot-9.10

代码

%% 准备
startup_rvc % 安装robot 工具箱
clear; % 清除工作空间的所有变量
clc; % 清除命令窗口的内容

%% 初始化参数
syms theta1 alpha1 a1 d1 theta2 alpha2 a2 d2 theta3 alpha3 a3 d3 d;% 参数变量
% 三个方程，三个齐次方程组
A1=[cos(theta1),-sin(theta1)*cos(alpha1),sin(theta1)*sin(alpha1),a1*cos(theta1);
    sin(theta1),cos(theta1)*cos(alpha1),-cos(theta1)*sin(alpha1),a1*sin(theta1);
    0,          sin(alpha1),             cos(alpha1),            d1            ;
    0,          0,                       0,                       1           ];

A2=[cos(theta2),-sin(theta2)*cos(alpha2),sin(theta2)*sin(alpha2),a2*cos(theta2);
    sin(theta2),cos(theta2)*cos(alpha2),-cos(theta2)*sin(alpha2),a2*sin(theta2);
    0,          sin(alpha2),            cos(alpha2),             d2            ;
    0,          0,                      0,                        1           ];

A3=[cos(theta3),-sin(theta3)*cos(alpha3),sin(theta3)*sin(alpha3),a3*cos(theta3);
    sin(theta3),cos(theta3)*cos(alpha3),-cos(theta3)*sin(alpha3),a3*sin(theta3);
    0,          sin(alpha3),            cos(alpha3),             d3            ;
    0,          0,                       0,                       1           ];

% 给变量赋值
a1 = sym(0.5);
alpha1 = sym(pi/2);
d1 = sym(0);

a2 = sym(1);
alpha2 = sym(-pi/2);
d2 = sym(0);

a3 = sym(1);
alpha3 = sym(0);
d3 = sym(0);

%% 运算
% 前三个自由度其次矩阵相乘，得到T(0,3)，即末端执行器相对于原点的坐标
T = eval(A1 * A2 * A3);
% 矩阵最右边一列，为末端执行器的X，Y，Z坐标
X_axis = T(1,4);% 末端执行器的X坐标
Y_axis = T(2,4) ;% 末端执行器的Y坐标
Z_axis = T(3,4);% 末端执行器的Z坐标

%给定末端执行器的终点，没有加约束条件，会得到复数的解，后期需要修改。
[sola,solu,solv] = solve(X_axis==1,Y_axis==0,Z_axis==0,theta1,theta2,theta3);
%求到一共有4组解，即四组转动的角度，我们只用第一组的解
solutions = [sola,solu,solv];

%原类型为syms，转变为double类型,x,y,z坐标，会出现复数的解
double_x = double(sign(real(solutions(1,1)))*abs(solutions(1,1)));
double_y = double(sign(real(solutions(1,2)))*abs(solutions(1,2)));
double_z = double(sign(real(solutions(1,3)))*abs(solutions(1,3)));

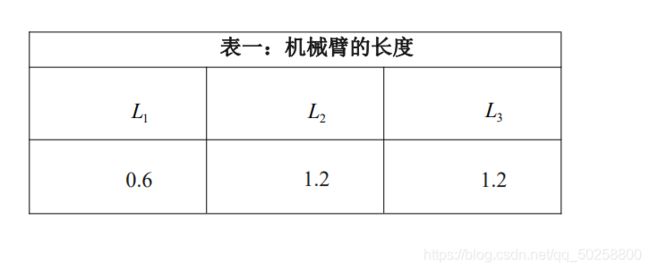
%% D-H参数
L1 = Link('d',0,'a',0.6,'alpha',pi/2);% Link类函数
L2 = Link('d',0,'a',1.2,'alpha',-pi/2);
L3 = Link('d',0,'a',1.2,'alpha',0);
robot = SerialLink([L1,L2,L3]); % SerialLink类函数，创建机器人可视化模型
robot.name = '旋转的机械臂';    % 机械臂名字

init_ang = [0 0 0]; % 起始的角度
targ_ang = [double_x,double_y,double_z]; % 结束时转过的角度,我们取齐次方程组的第一组解
step=80; % 时间矢量长度T
[q,qd,qdd] = jtraj(init_ang,targ_ang,step);
% jtraj函数：计算两点之间一个关节的空间轨迹，利用5阶quintic多项式来表示速度和加速度。
% q为空间轨迹，qd为速度，qdd为加速度

grid on
T = robot.fkine(q);%根据插值，求得末端执行器的位姿                                          
plot3(squeeze(T(1,4,:)),squeeze(T(2,4,:)),squeeze(T(3,4,:)));%画出末端轨迹
hold on
robot.plot(q,'tilesize',2);%动画演示