材料力学
文章目录
- 第1章 绪论
-
- 1.1 材料力学的任务
- 1.2 变形固体的基本假设
- 1.3 外力及其分类
- 1.4 内力、截面法和应力的概念
- 1.5 变形与应变
- 1.6 杆件变形的基本形式
- 第2章 拉伸、压缩与剪切
-
- 2.1 轴向拉伸与压缩的概念和实例
- 2.2 直杆轴向拉伸或压缩时横截面上的内力和应力
- 2.3 直杆轴向拉伸或压缩时斜截面上的应力
- 2.4 材料拉伸时的力学性能
- 2.5 材料压缩时的力学性能
- 2.6 温度和时间圣材料力学性能的影响
- 2.7 失效、安全因数和强度计算
- 2.8 轴向拉伸或压缩时的变形
- 2.9 轴向拉伸或压缩的应变能
- 2.10 拉伸、压缩的超静定问题
- 2.11 温度应力和装配应力
- 2.12 应力集中的概念
- 2.13 剪切和挤压的实用计算
- 第3章 扭转
-
- 3.1 扭转的概念和实例
- 3.2 外力偶矩的计算、扭矩和扭矩图
- 3.3 纯剪切
- 3.4 圆轴扭转时的应力
- 3.5 圆轴扭转时的变形
- 3.6 圆柱形密圈螺旋弹簧的应力和变形
- 3.7 非圆截面杆扭转的概述
- 3.8 薄壁杆件的自由扭转
- 第4章 弯曲内力
-
- 4.1 弯曲的概念和实例
- 4.2 受弯杆件的简化
- 4.3 剪力和弯矩
- 4.4 剪力方程和弯矩方程、剪力图和弯矩图
- 4.5 载荷集度、剪力和弯矩间的关系
- 4.6 平面曲杆的弯曲内力
- 第5章 弯曲应力
-
- 5.1 纯弯曲
- 5.2 纯弯曲时的正应力
- 5.3 横力弯曲时的正应力
- 5.4 弯曲切应力
- 5.5 关于弯曲理论的基本假设
- 5.6 提高弯曲强度的措施
- 第6章 弯曲变形
-
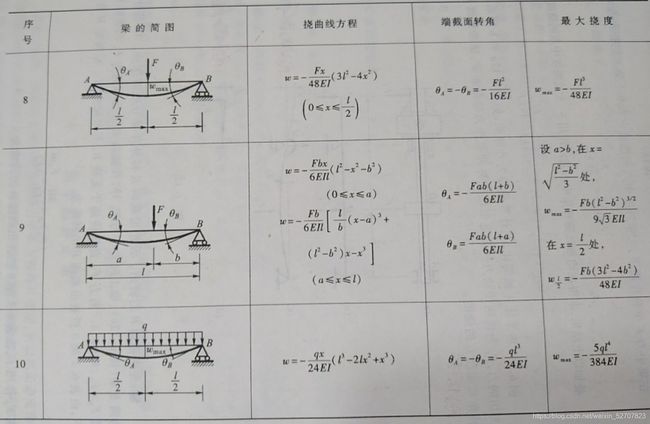
- 6.1 工程中的弯曲变形问题
- 6.2 挠曲线的微分方程
- 6.3 用积分法求弯曲变形
- 6.4 用叠加法求弯曲变形
- 6.5 简单超静定梁
- 6.6 减小弯曲变形的一些措施
- 第7章 应力和应变分析、强度理论
-
- 7.1 应力状态概述
- 二向和三向应力状态实例
第1章 绪论
1.1 材料力学的任务
强度要求:构件有足够的抵抗破坏的能力
刚度要求:构件有足够的抵抗变形的能力
稳定性要求:构件有足够的保持原有平衡形态的能力
任务:在满足以上要求前提下,为设计既经济又安全的构件,提供必要的理论基础和计算方法
1.2 变形固体的基本假设
连续性假设:组成固体的物质不留空隙地充满固体体积
均匀性假设:任何一部分的力学性能相同
各向同性假设:沿不同方向的力学性能都相同
小变形与线弹性范围:变形范围很微小
1.3 外力及其分类
外力可分为表面力和体积力、静载荷和动载荷
1.4 内力、截面法和应力的概念
内力:受外力而变形,其内部各部分之间相对位置改变而引起的相互作用
截面上的内力:分布内力系向截面上某一点简化后得到的合力和合力偶
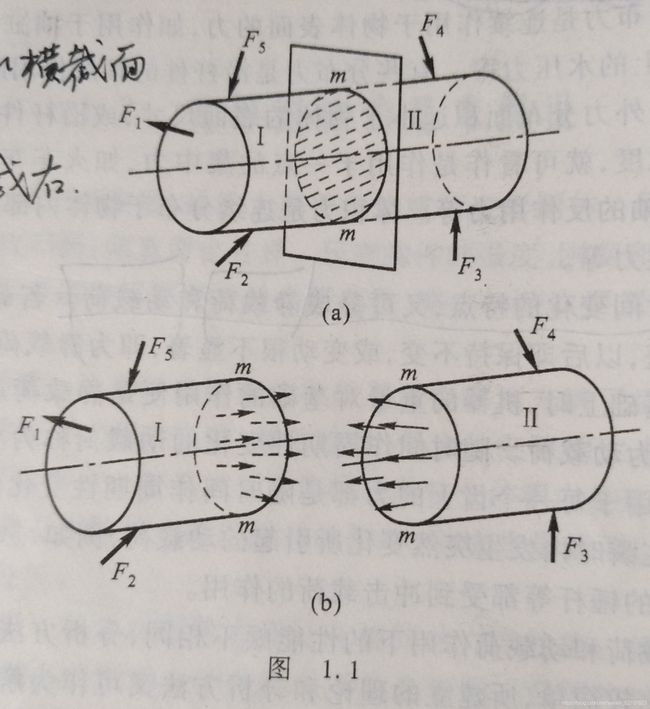
截面法:
(1)沿截面假想切成两段,取任一段为研究对象
(2)以作用于截面上的内力代替弃去部分对取出部分的作用
(3)建立取出部分的平衡方程,确定未知的内力
1.5 变形与应变
应变: ε = lim Δ x → 0 Δ s Δ x \varepsilon=\displaystyle\lim_{\Delta x\rightarrow0}\dfrac{\Delta s}{\Delta x} ε=Δx→0limΔxΔs,其中 Δ s \Delta s Δs为长度变化, Δ x \Delta x Δx为原长
角应变: γ = lim M N ‾ , M L ‾ → 0 ( π 2 − ∠ L ′ M ′ N ′ ) \gamma=\displaystyle\lim_{\overline{MN},\overline{ML}\rightarrow0}(\dfrac{\pi}{2}-\angle{L'M'N'}) γ=MN,ML→0lim(2π−∠L′M′N′)
1.6 杆件变形的基本形式
杆:长度远大于横截面尺寸的构件
拉伸、压缩
剪切
扭转
弯曲
第2章 拉伸、压缩与剪切
2.1 轴向拉伸与压缩的概念和实例
作用于杆件上的外力合力的作用线与杆件轴线重合,杆件变形是沿轴线方向的伸长或缩短
2.2 直杆轴向拉伸或压缩时横截面上的内力和应力
将内力称为轴力,规定拉为正,压为负
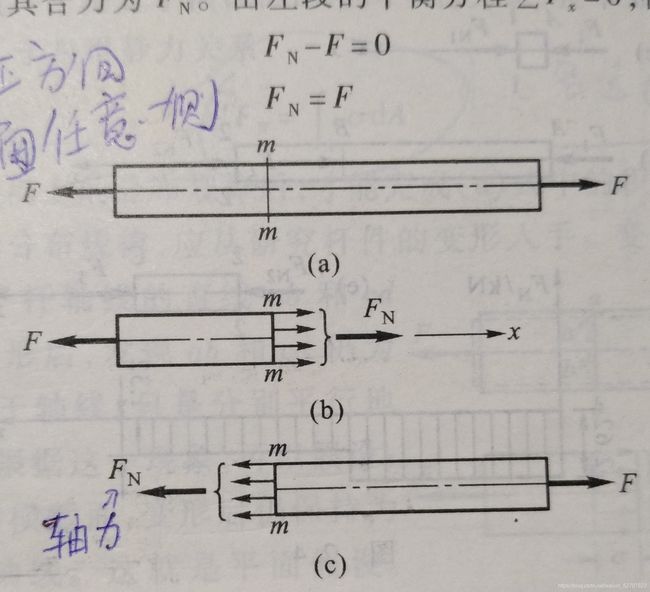
应力 σ = F N A \sigma=\dfrac{F_N}{A} σ=AFN
圣维南原理:如用与外力系静力等效的合力来代替原力系,则除在原力系作用区域内有明显差别外,在离外力作用区域略远处(距离约等于横截面尺寸处),上述替代的影响非常微小
2.3 直杆轴向拉伸或压缩时斜截面上的应力
σ = F A \sigma=\dfrac{F}{A} σ=AF, A α = A cos α A_{\alpha}=\dfrac{A}{\cos{\alpha}} Aα=cosαA
F α = F F_{\alpha}=F Fα=F,
将k-k截面的应力分解:
σ α = σ cos 2 α \sigma_{\alpha}=\sigma\cos^2{\alpha} σα=σcos2α
τ α = σ 2 sin 2 α \tau_{\alpha}=\dfrac{\sigma}{2}\sin{2\alpha} τα=2σsin2α
σ α m a x = σ \sigma_{\alpha max}=\sigma σαmax=σ
τ α m a x = σ 2 \tau_{\alpha max}=\dfrac{\sigma}{2} ταmax=2σ

2.4 材料拉伸时的力学性能
低碳钢:含碳量0.3%以下的碳素钢

σ p 为 比 例 极 限 \sigma_p为比例极限 σp为比例极限, σ e \sigma_e σe弹性极限, σ s \sigma_s σs为屈服极限, σ b \sigma_b σb为强度极限
ε = Δ l l \varepsilon=\dfrac{\Delta l}{l} ε=lΔl
oa段:比例极限, σ = E ε \sigma=E\varepsilon σ=Eε
ab段:弹性极限, E = σ ε = tan α E=\dfrac{\sigma}{\varepsilon}=\tan{\alpha} E=εσ=tanα,大于弹性极限后,卸载拉力后会发生塑性变形
ob:弹性阶段,满足胡克定律,称材料是线弹性的
bc:屈服阶段, σ s \sigma_s σs为下屈服极限,称屈服极限
ce:强化阶段,恢复了抵抗变形的能力,称为材料强化,用 σ b \sigma_b σb表示,称强度极限或抗拉强度
ef:局部变形阶段,出现缩颈现象
f ′ h f'h f′h称为弹性恢复长度
伸长率: δ = l 1 − l l × 100 % \delta=\dfrac{l_1-l}{l}\times100\% δ=ll1−l×100%
断面收缩率: ψ = A − A 1 A × 100 % \psi=\dfrac{A-A_1}{A}\times100\% ψ=AA−A1×100%
卸载定律:把试样拉超过d点,再卸载拉力, d d ′ dd' dd′近似平行于 o a oa oa,说明在卸载过程中,应力和应变按直线规律变化, d g ′ dg' dg′表示消失了的弹性变形, o d ′ od' od′表示不再消失的塑性变形
冷作硬化:卸载拉力后,如果在短期内再加载拉力,则应力和应变间的关系大致上沿卸载时的斜直线 d ′ d d'd d′d变化,其比例极限提高,但塑性变形却减少了,伸长率也减小了,称这种现象为冷作硬化,经退火处理可消除
对于没有明显屈服阶段的塑性材料,可以将产生0.2%塑性应变时的应力作为屈服指标,称为名义屈服极限,用 σ 0.2 \sigma_{0.2} σ0.2表示
铸铁用强度极限 σ b \sigma_b σb表示,它没有屈服极限
2.5 材料压缩时的力学性能
低碳钢压缩时的弹性模量 E E E和 σ s \sigma_s σs都与拉伸时大致相同,进入屈服阶段后,试样横截面积不断增大,抗压能力继续增强,因而得不到压缩时的强度极限

铸铁破坏断面的法线与轴线大致成 45 ° ∼ 55 ° 45\degree \sim 55\degree 45°∼55°倾角,表明试样沿斜截面因相对错动而破坏
脆性材料抗拉强度低,抗压能力强
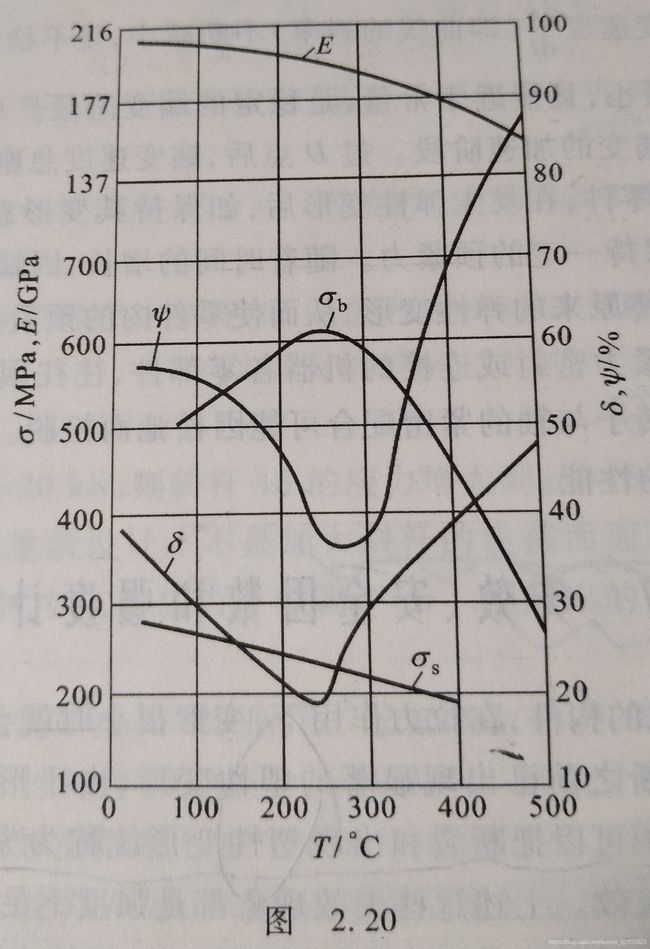
2.6 温度和时间圣材料力学性能的影响
2.7 失效、安全因数和强度计算
可以把材料断裂和出现塑性变形统称为失效
极限应力:脆性材料断裂时的强度极限是 σ b \sigma_b σb,塑性材料屈服时的应力是屈服极限 σ s \sigma_s σs
许用应力:以大于1的因数除极限应力,用 [ σ ] [\sigma] [σ]表示,对塑性材料 [ σ ] = σ s n s [\sigma]=\dfrac{\sigma_s}{n_s} [σ]=nsσs,对脆性材料 [ σ ] = σ b n b [\sigma]=\dfrac{\sigma_b}{n_b} [σ]=nbσb,把 n s n_s ns和 n − b n-b n−b称为安全因数
构件轴向拉伸或压缩时的强度条件为 σ = F N A ≤ [ σ ] \sigma=\dfrac{F_N}{A}\leq[\sigma] σ=AFN≤[σ]
2.8 轴向拉伸或压缩时的变形
杆在轴线方向的伸长为 Δ l = l 1 − l \Delta l=l_1-l Δl=l1−l,线应变 ε = Δ l l \varepsilon=\dfrac{\Delta l}{l} ε=lΔl,应力 σ = F A \sigma=\dfrac{F}{A} σ=AF,胡克定律 σ = E ε \sigma=E\varepsilon σ=Eε, E E E为弹性模量
Δ l = F l E A \Delta l=\dfrac{Fl}{EA} Δl=EAFl
E A EA EA称为抗拉/压刚度,越大则 Δ l \Delta l Δl越小
横向应变(横截面) ε ′ = b 1 − b b \varepsilon'=\dfrac{b_1-b}{b} ε′=bb1−b
泊松比 μ = ∣ ε ′ ε ∣ \mu=\lvert\dfrac{\varepsilon'}{\varepsilon}\rvert μ=∣εε′∣
2.9 轴向拉伸或压缩的应变能
应变能:弹性固体在外力作用下,因变形而储存的能量称为应变能
V ε = W = 1 2 F Δ l = F 2 l 2 E A V_{\varepsilon}=W=\dfrac{1}{2}F\Delta l=\dfrac{F^2l}{2EA} Vε=W=21FΔl=2EAF2l
单位体积内的应变能: v ε = 1 2 σ ε = σ 2 2 E v_{\varepsilon}=\dfrac{1}{2}\sigma\varepsilon=\dfrac{\sigma^2}{2E} vε=21σε=2Eσ2
整体的应变能: V ε = ∫ V v ε d V V_{\varepsilon}=\displaystyle\int_V{v_{\varepsilon}dV} Vε=∫VvεdV
2.10 拉伸、压缩的超静定问题
静力平衡方程数量少于未知力的个数,称为超静定问题,未知力个数减去方程数得几,就称为几次超静定问题
这类方程通常要补充变形协调方程
2.11 温度应力和装配应力
Δ l T = α l Δ T ⋅ l \Delta l_T=\alpha_l \Delta T\cdot l ΔlT=αlΔT⋅l, α l \alpha_l αl为材料的线胀系数
在管道中增加伸缩节,在钢轨各段之间留有伸缩缝等,可以削弱温度应力的不良影响
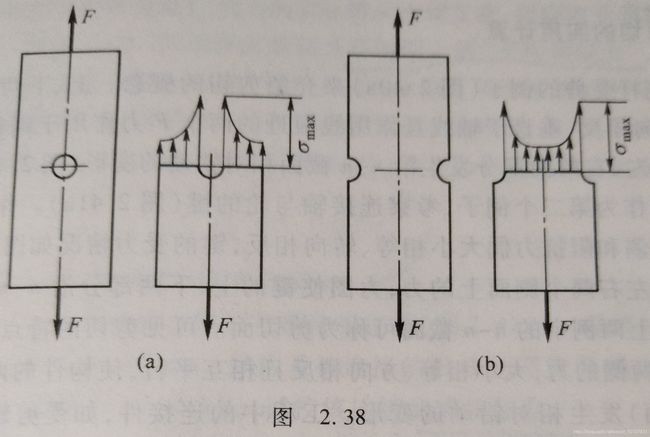
2.12 应力集中的概念
在零件尺寸突然改变处的横截面上,应力并不是均匀分布的,在开口处应力急剧上升,称为应力集中,截面尺寸改变得越急剧、角越尖、孔越小,应力集中的程度就越严重
2.13 剪切和挤压的实用计算
剪切:
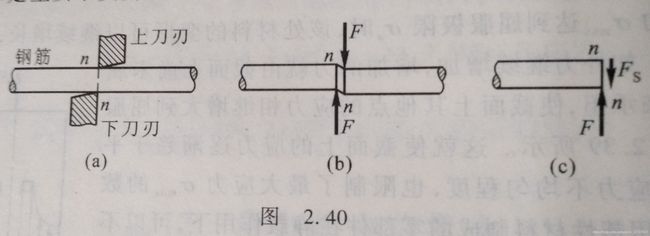
τ = F S A ≤ [ τ ] \tau=\dfrac{F_S}{A}\leq [\tau] τ=AFS≤[τ]
挤压:

σ b s = F A b s ≤ [ σ b s ] \sigma_{bs}=\dfrac{F}{A_{bs}}\leq[\sigma_{bs}] σbs=AbsF≤[σbs]
第3章 扭转
3.1 扭转的概念和实例
扭转:力偶矩大小相等、转向相反且作用平面垂直于杆件轴线,使杆件绕轴线转运

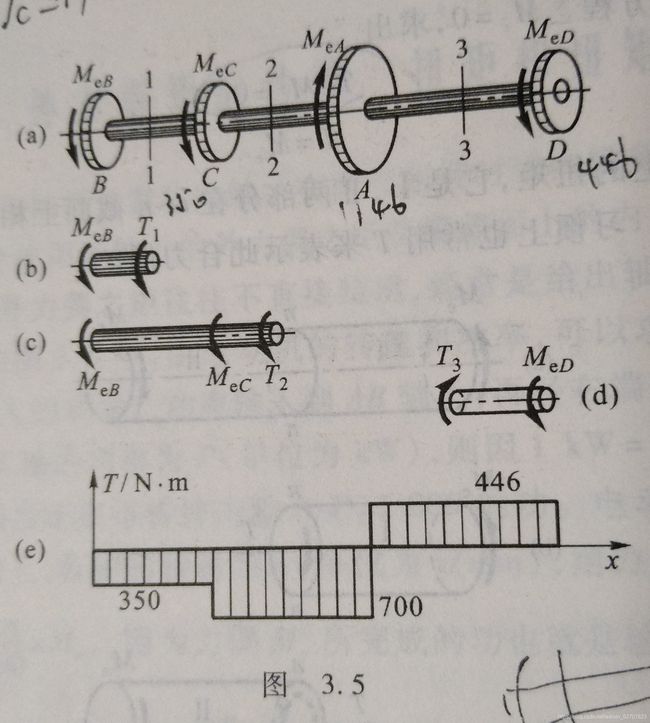
3.2 外力偶矩的计算、扭矩和扭矩图
力偶 M e M_e Me在每秒钟内完成的功应为 2 π × n 60 × M e = P × 1000 2\pi\times\dfrac{n}{60}\times M_e=P\times1000 2π×60n×Me=P×1000,得
{ M e } N ⋅ m = 9549 { P } k W { n } r / m i n \{M_e\}_{N\cdot m}=9549\dfrac{\{P\}_{kW}}{\{n\}_{r/min}} {Me}N⋅m=9549{n}r/min{P}kW,习惯上用 T T T表示截面上的扭矩
3.3 纯剪切
薄壁圆筒扭转时的切应力: M e = 2 π r δ ⋅ τ ⋅ r M_e=2\pi r \delta\cdot\tau\cdot r Me=2πrδ⋅τ⋅r,得 τ = M e 2 π r 2 δ \tau=\dfrac{M_e}{2\pi r^2\delta} τ=2πr2δMe
壁厚为1/10的平均半径为薄壁
切应力互等定理:在单元体相互垂直的两个平面上,切应力必然成对存在,且数值相等;两者都垂直于两个平面的交线,方向则共同指向或共同背离这一交线。 τ = τ ′ \tau=\tau' τ=τ′
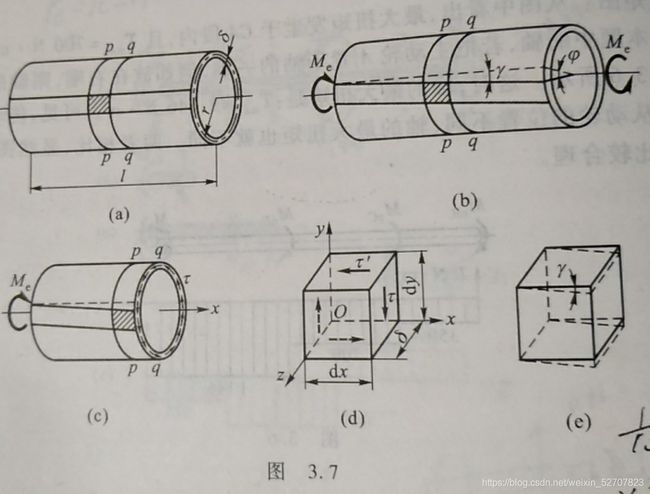
切应变:侧面只有切应力没有正应力,称为纯剪切,切应变: γ = r φ l \gamma=\dfrac{r\varphi}{l} γ=lrφ
剪切胡克定律: τ = G γ \tau=G\gamma τ=Gγ, G G G为切变模量
G = E 2 ( 1 + μ ) G=\dfrac{E}{2(1+\mu)} G=2(1+μ)E
剪切应变能: d V ε = d W = ( ∫ 0 γ 1 τ d γ ) d V dV_{\varepsilon}=dW=(\int_0^{\gamma_1}\tau d\gamma)dV dVε=dW=(∫0γ1τdγ)dV
单位体积内的剪切应变能(应变能密度): v ε = d V ε d V = ∫ 0 γ 1 τ d γ = 1 2 τ γ = τ 2 2 G v_{\varepsilon}=\dfrac{dV_{\varepsilon}}{dV}=\int_0^{\gamma_1}\tau d\gamma=\dfrac{1}{2}\tau\gamma=\dfrac{\tau^2}{2G} vε=dVdVε=∫0γ1τdγ=21τγ=2Gτ2
3.4 圆轴扭转时的应力
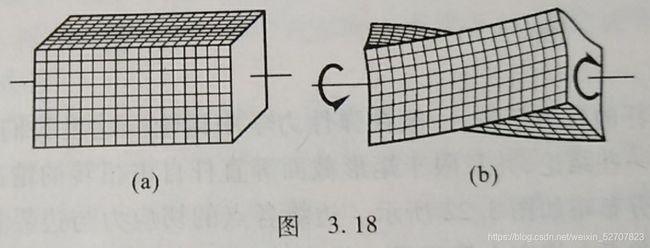
变形几何关系:等直圆轴扭转变形前原为平面的横截面,变形后仍保持为平面,形状和大小不变,半径仍保持为直线;且相邻横截面间的距离不变。这是圆轴扭转的平面假设
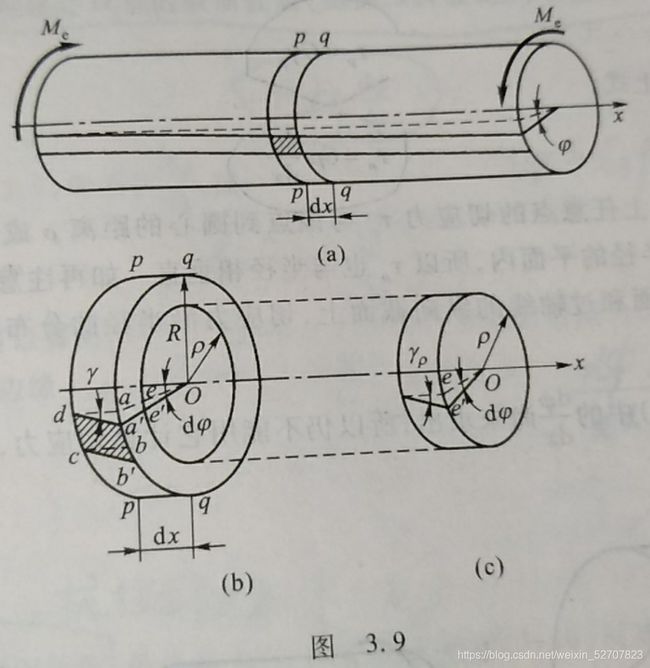
γ ρ = ρ d φ d x \gamma_{\rho}=\rho\dfrac{d\varphi}{dx} γρ=ρdxdφ
物理关系: τ ρ = G γ ρ \tau_{\rho}=G\gamma_{\rho} τρ=Gγρ
静力关系: T = ∫ A ρ τ ρ d A = G d φ d x ∫ A ρ 2 d A = G I p d φ d x T=\int_A{\rho\tau_{\rho}dA}=G\dfrac{d\varphi}{dx}\displaystyle\int_A{\rho^2dA}=GI_p\dfrac{d\varphi}{dx} T=∫AρτρdA=Gdxdφ∫Aρ2dA=GIpdxdφ, I p I_p Ip为截面极惯性矩,单位 m 4 m^4 m4
τ ρ = T ρ I p \tau_{\rho}=\dfrac{T\rho}{I_p} τρ=IpTρ,则最大的切应力为 τ m a x = T R I p \tau_{max}=\dfrac{TR}{I_p} τmax=IpTR
用 W t = I p R W_t=\dfrac{I_p}{R} Wt=RIp为抗扭截面系数,单位 m 3 m^3 m3,得 τ m a x = T W t \tau_{max}=\dfrac{T}{W_t} τmax=WtT
对实心圆轴, I p = π D 4 32 I_p=\dfrac{\pi D^4}{32} Ip=32πD4, W t = π D 3 16 W_t=\dfrac{\pi D^3}{16} Wt=16πD3
对空心圆轴, α = d / D \alpha=d/D α=d/D, I p = π D 4 32 ( 1 − α 4 ) I_p=\dfrac{\pi D^4}{32}(1-\alpha^4) Ip=32πD4(1−α4), W t = π D 3 16 ( 1 − α 4 ) W_t=\dfrac{\pi D^3}{16}(1-\alpha^4) Wt=16πD3(1−α4)
τ m a x = T m a x W t ≤ [ τ ] \tau_{max}=\dfrac{T_{max}}{W_t}\leq[\tau] τmax=WtTmax≤[τ]
3.5 圆轴扭转时的变形
扭转角 d φ = T G I p d x d\varphi=\dfrac{T}{GI_p}dx dφ=GIpTdx
φ = T l G I p \varphi=\dfrac{Tl}{GI_p} φ=GIpTl
单位长度扭转角 φ ′ = T G I p = φ l \varphi'=\dfrac{T}{GI_p}=\dfrac{\varphi}{l} φ′=GIpT=lφ
φ m a x ′ = T m a x G I p × 180 ° π ≤ [ φ ′ ] \varphi'_{max}=\dfrac{T_{max}}{GI_p}\times\dfrac{180\degree}{\pi}\leq[\varphi'] φmax′=GIpTmax×π180°≤[φ′]
3.6 圆柱形密圈螺旋弹簧的应力和变形
3.7 非圆截面杆扭转的概述
翘曲:变形后杆的横截面已不再保持为平面
3.8 薄壁杆件的自由扭转
第4章 弯曲内力
4.1 弯曲的概念和实例
作用于杆件上的外力垂直于传杆件的轴线,使原为直线的轴线变形为曲线
对称弯曲:作用于杆件上的所有外力都在纵向对称面内时,弯曲变形轴线也将是位于这个对称面内的一条曲线
4.2 受弯杆件的简化
支座的几种基本形式:
铰支座:可动铰支座、固定铰支座



载荷简化:集中力、均布载荷

静定梁的基本形式:
简支梁:一端固定铰一端可动铰
外伸梁:一端伸出支座外
悬臂梁:一端固定一端自由
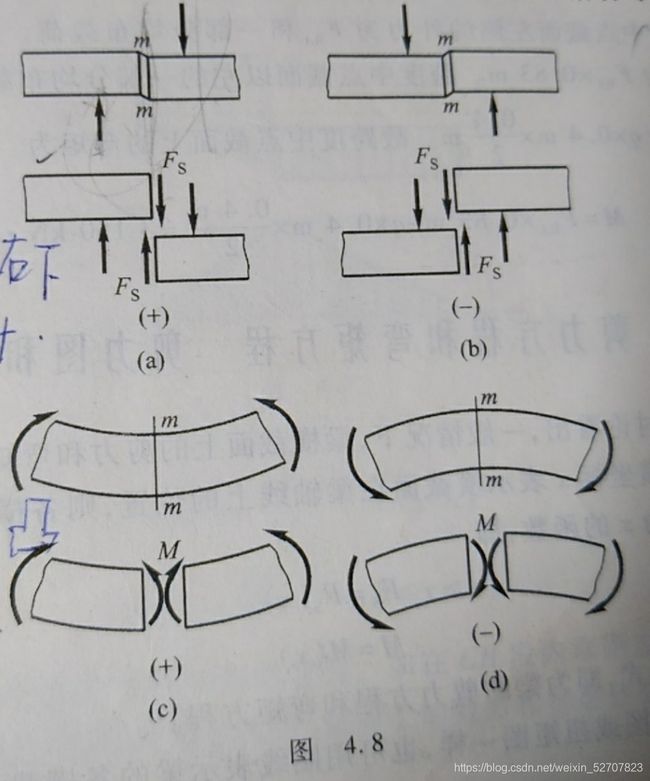
4.3 剪力和弯矩
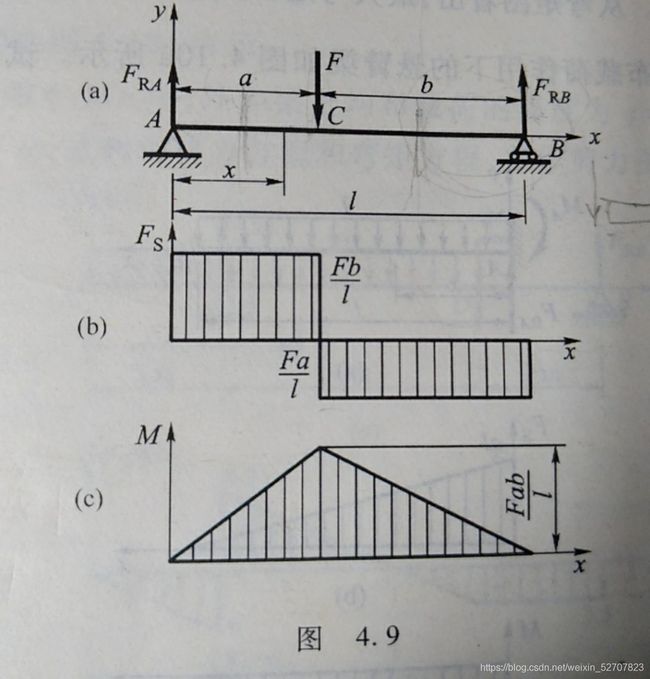
4.4 剪力方程和弯矩方程、剪力图和弯矩图
4.5 载荷集度、剪力和弯矩间的关系
梁上分布载荷的集度 q ( x ) q(x) q(x)是 x x x的连续函数,且规定 q ( x ) q(x) q(x)向上为正
q ( x ) = d F S ( x ) d x , F S ( x ) = d M ( x ) d x q(x)=\dfrac{dF_S(x)}{dx},F_S(x)=\dfrac{dM(x)}{dx} q(x)=dxdFS(x),FS(x)=dxdM(x)
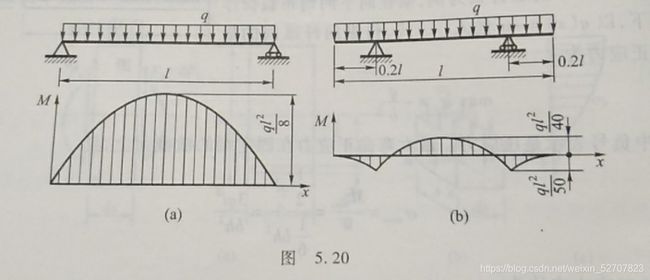
(1)梁中若无载荷分布, d F S ( x ) d x = q ( x ) = 0 \dfrac{dF_S(x)}{dx}=q(x)=0 dxdFS(x)=q(x)=0, F S ( x ) = C F_S(x)=C FS(x)=C,剪力图是平行于x轴的直线,弯矩图是斜直线
(2)在梁的某段内,若作用均布载荷,即 q ( x ) = C q(x)=C q(x)=C,则剪力图是斜直线,弯矩图是抛物线
(3)在梁的某一截面上,若 F S ( x ) = d M ( x ) d x = 0 F_S(x)=\dfrac{dM(x)}{dx}=0 FS(x)=dxdM(x)=0,则在这一截面上弯矩有一极值,在剪力为0的截面上
4.6 平面曲杆的弯曲内力
第5章 弯曲应力
5.1 纯弯曲
弯矩只与横截面上的正应力 σ \sigma σ相关,剪力与切应力 τ \tau τ相关
梁上既有弯矩又有剪力,称为横力弯曲或剪切弯曲
纯弯曲:只有正应力而无切应力,剪力为零,弯矩为常量
弯曲的平面假设:变形前原为平面的梁横截面变形后仍保持为平面
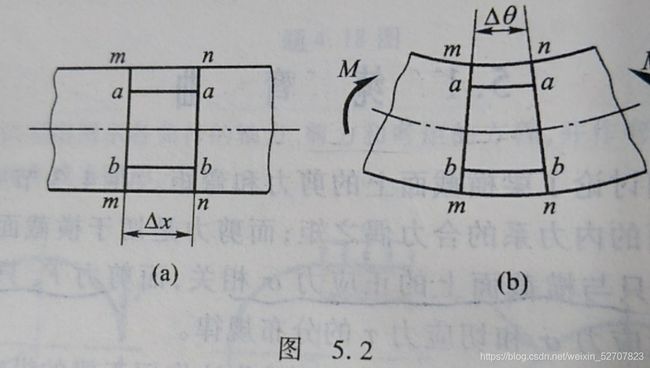
中性层:弯曲后纤维长度不变的层
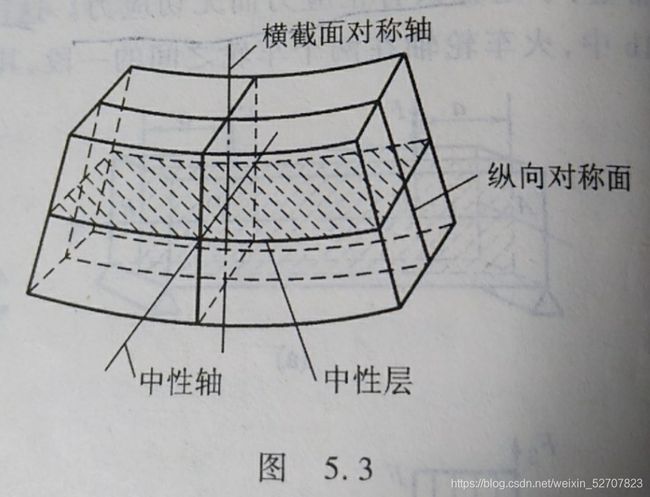
纯弯曲两个假设:(1)平面假设;(2)纵向纤维间无正应力
5.2 纯弯曲时的正应力
变形的几何关系:变形前相距为 d x dx dx的两个横截面,变形后绕各自的中性轴转运,两横截面的相对转角 d θ d\theta dθ,并保持为平面
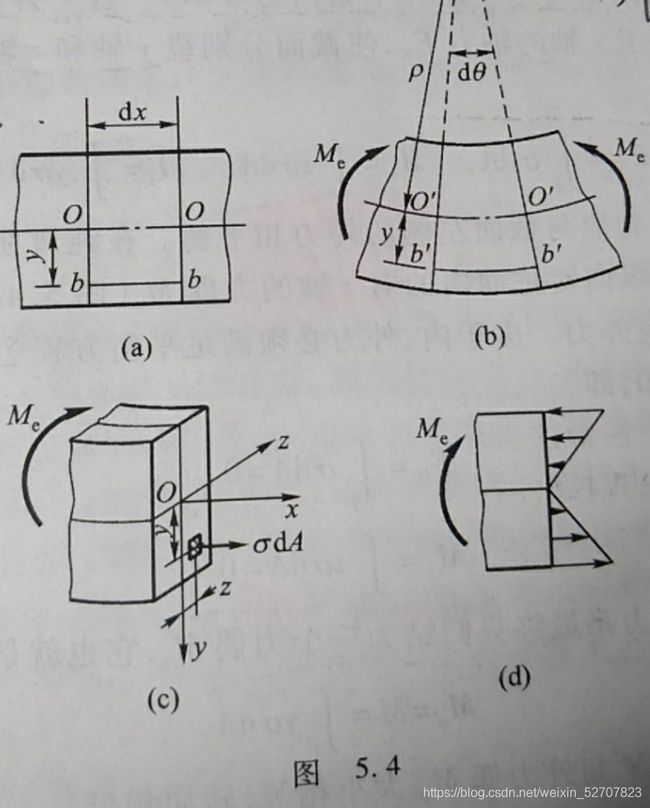
ρ \rho ρ为中性层的曲率半径, b b bb bb的应变为 ε = y ρ \varepsilon=\dfrac{y}{\rho} ε=ρy,可见,纵向纤维的应变与它到中性层的距离成正比
物理关系:因为纵向纤维之间无正应力,每一线段都是单向拉伸或压缩,得 σ = E y ρ \sigma=E\dfrac{y}{\rho} σ=Eρy
静力关系:中性轴通过截面形心又包含在中性层内,所以梁截面的形心连线也在中性层内,变形后其长度不变, I z = ∫ y 2 d A I_z=\int{y^2dA} Iz=∫y2dA, M = E ρ ∫ A y 2 d A M=\dfrac{E}{\rho}\int_A{y^2dA} M=ρE∫Ay2dA,曲率 1 ρ = M E I z \dfrac{1}{\rho}=\dfrac{M}{EI_z} ρ1=EIzM,将 E I z EI_z EIz称为抗弯刚度, σ = M y I z \sigma=\dfrac{My}{I_z} σ=IzMy
要确定横截面上的分布内力系对梁变形的影响,最简单的方法是将内力系向横截面的形心主惯性轴简化
5.3 横力弯曲时的正应力
W = I z y m a x W=\dfrac{I_z}{y_{max}} W=ymaxIz
σ m a x = M m a x W \sigma_{max}=\dfrac{M_{max}}{W} σmax=WMmax, W W W为抗弯截面系数,单位 m 3 m^3 m3
若高为h,宽为b的矩形,则 W = I z h / 2 = b h 2 6 W=\dfrac{I_z}{h/2}=\dfrac{bh^2}{6} W=h/2Iz=6bh2
若截面是直径为d的圆形,则 W = π d 3 32 W=\dfrac{\pi d^3}{32} W=32πd3
σ m a x = M m a x W ≤ [ σ ] \sigma_{max}=\dfrac{M_{max}}{W}\leq[\sigma] σmax=WMmax≤[σ]
5.4 弯曲切应力
矩形截面梁:
假设
(1)横截面上各点的切应力的方向都平行于剪力 F S F_S FS
(2)切应力沿截面宽度均匀分布
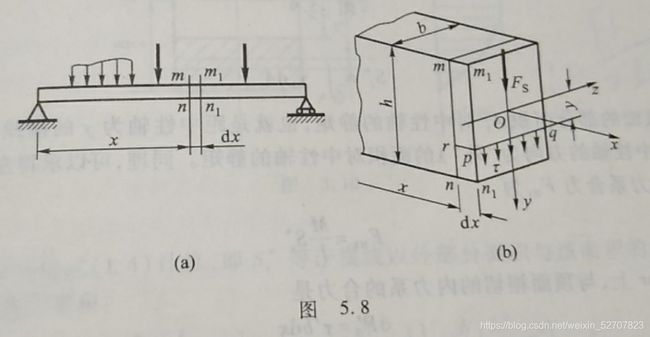
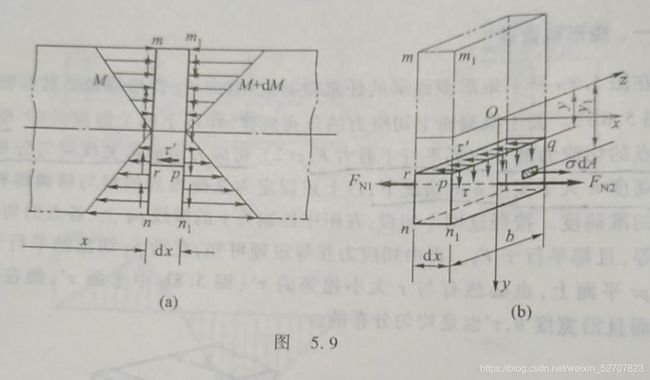
F N 2 = ∫ A 1 σ d A = ( M + d M ) I z S z ∗ F_{N2}=\displaystyle\int_{A1}{\sigma dA}=\dfrac{(M+dM)}{I_z}S^*_z FN2=∫A1σdA=Iz(M+dM)Sz∗
S z ∗ = ∫ A 1 y 1 d A S_z^*=\displaystyle\int_{A_1}{y_1dA} Sz∗=∫A1y1dA,为截面上距中性轴为 y y y的横线以外部分面积对中性轴的静矩
F N 1 = M I z S z ∗ F_{N1}=\dfrac{M}{I_z}S_z^* FN1=IzMSz∗
d F S ′ = τ ′ b d x dF'_S=\tau'bdx dFS′=τ′bdx
F N 2 − F N 1 − d F S ′ = 0 F_{N2}-F_{N1}-dF'_S=0 FN2−FN1−dFS′=0
τ = τ ′ = F S S z ∗ I z b \tau=\tau'=\dfrac{F_S S^*_z}{I_z b} τ=τ′=IzbFSSz∗
矩形截面 S z ∗ = b 2 ( h 2 4 − y 2 ) S^*_z=\dfrac{b}{2}(\dfrac{h^2}{4}-y^2) Sz∗=2b(4h2−y2), τ = F S 2 I z ( h 2 4 − y 2 ) \tau=\dfrac{F_S}{2I_z}(\dfrac{h^2}{4}-y^2) τ=2IzFS(4h2−y2)

τ m a x = F S h 2 8 I z = 3 2 F S b h \tau_{max}=\dfrac{F_S h^2}{8I_z}=\dfrac{3}{2}\dfrac{F_S}{bh} τmax=8IzFSh2=23bhFS,说明矩形截面梁的最大切应力为平均切应力 F S b h \dfrac{F_S}{bh} bhFS的1.5倍
工字形截面梁:
τ = F S I z b 0 [ b 8 ( h 2 − h 0 2 ) + b 0 2 ( h 2 4 − y 2 ) ] \tau=\dfrac{F_S}{I_zb_0}[\dfrac{b}{8}(h^2-h^2_0)+\dfrac{b_0}{2}(\dfrac{h^2}{4}-y^2)] τ=Izb0FS[8b(h2−h02)+2b0(4h2−y2)]

τ m a x = F S I z b 0 [ b h 2 8 − ( b − b 0 ) h 0 2 8 ] \tau_{max}=\dfrac{F_S}{I_z b_0}[\dfrac{bh^2}{8}-(b-b_0)\dfrac{h_0^2}{8}] τmax=Izb0FS[8bh2−(b−b0)8h02]
τ m i n = F S I z b 0 [ b h 2 8 − b h 0 2 8 ] \tau_{min}=\dfrac{F_S}{I_z b_0}[\dfrac{bh^2}{8}-\dfrac{bh_0^2}{8}] τmin=Izb0FS[8bh2−8bh02]
两者相差不大,可以认为是受力均匀,近似得 τ = F S b 0 h 0 \tau=\dfrac{F_S}{b_0h_0} τ=b0h0FS
圆形截面:
假设弦AB上各点切应力的垂直分量 τ y = F S S z ∗ I z b \tau_y=\dfrac{F_S S_z^*}{I_z b} τy=IzbFSSz∗是相等的
S z ∗ = π R 2 2 ⋅ 4 R 3 π S_z^*=\dfrac{\pi R^2}{2}\cdot \dfrac{4R}{3\pi} Sz∗=2πR2⋅3π4R, I z = π R 4 4 I_z=\dfrac{\pi R^4}{4} Iz=4πR4
τ m a x = 4 3 F S π R 2 \tau_{max}=\dfrac{4}{3}\dfrac{F_S}{\pi R^2} τmax=34πR2FS,平均应力为 F S π R 2 \dfrac{F_S}{\pi R^2} πR2FS,最大应力为平均应力的4/3
5.5 关于弯曲理论的基本假设
平面假设
纵向纤维间无正应力
材料是线弹性的
当截面高度远小于跨度 h ≪ l h\ll l h≪l,由平面假设引起的误差非常小,这正是杆的几何特征

一般情况下 σ y \sigma_y σy是可以省略的,这是假设纵向纤维间无正应力的依据
5.6 提高弯曲强度的措施
选择梁截面的合理形状:截面面积小且抗弯截面系数越大越有利

σ t m a x σ c m a x = y 1 y 2 = [ σ t ] [ σ c ] \dfrac{\sigma_{tmax}}{\sigma_{cmax}}=\dfrac{y_1}{y_2}=\dfrac{[\sigma_t]}{[\sigma_c]} σcmaxσtmax=y2y1=[σc][σt]
变截面梁:截面尺寸沿轴线变化的梁
等强度梁:变截面梁各横截面上的最大正应力都相等,且都等于许用应力
σ m a x = M ( x ) W ( x ) = [ σ ] \sigma_{max}=\dfrac{M(x)}{W(x)}=[\sigma] σmax=W(x)M(x)=[σ],代入 h = C h=C h=C,得 b ( x ) b(x) b(x), τ m a x = [ τ ] \tau_{max}=[\tau] τmax=[τ],得 b m i n b_{min} bmin,或者是 b = C b=C b=C最后求出 h m i n h_{min} hmin
第6章 弯曲变形
6.1 工程中的弯曲变形问题
机床主轴发生弯曲,影响精度
6.2 挠曲线的微分方程
挠曲线:在对称弯曲的情况下,变形后梁的轴线将变成平面内的一条曲线
用 w w w来表示挠度,表示坐标为 x x x的横截面的形心沿 y y y方向的位移, w = f ( x ) w=f(x) w=f(x)

截面转角:弯曲变形中,梁的横截面对其原来位置转过的角度 θ \theta θ, tan θ = d w d x ≈ θ \tan{\theta}=\dfrac{dw}{dx} \approx\theta tanθ=dxdw≈θ
向上的挠度和逆时针方向的转角为正,反之为负
1 ρ = M E I \dfrac{1}{\rho}=\dfrac{M}{EI} ρ1=EIM
推导过程略,最终得挠曲线的近似微分方程 d 2 w d x 2 = M E I \dfrac{d^2w}{dx^2}=\dfrac{M}{EI} dx2d2w=EIM
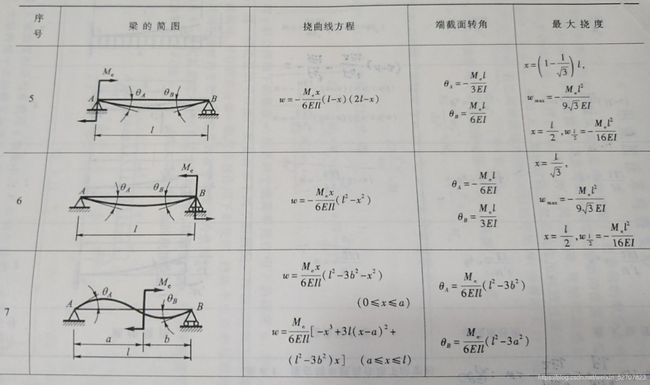
6.3 用积分法求弯曲变形
w = ∬ ( M E I d x ) d x + C x + D w=\displaystyle\iint{(\dfrac{M}{EI}dx)dx}+Cx+D w=∬(EIMdx)dx+Cx+D
挠曲线的任意点上,有唯一确定的挠度和转角,这个是连续性条件,可确定积分常数
∣ w ∣ m a x ≤ [ w ] |w|_{max}\leq[w] ∣w∣max≤[w], ∣ θ ∣ m a x ≤ [ θ ] |\theta|_{max}\leq[\theta] ∣θ∣max≤[θ]
6.4 用叠加法求弯曲变形
M = M F + M q M=M_F+M_q M=MF+Mq,集中载荷和均布载荷产生的弯矩
E I d 2 w d x 2 = E I d 2 ( w F + w q ) d x 2 EI\dfrac{d^2w}{dx^2}=EI\dfrac{d^2(w_F+w_q)}{dx^2} EIdx2d2w=EIdx2d2(wF+wq)
6.5 简单超静定梁
增加变形协调方程
6.6 减小弯曲变形的一些措施
改善结构形式和载荷作用方式,减小弯矩
选择合理的截面形状:起重机大梁使用工字形或箱形截面;机器箱体采用加筋而不是增加壁厚
第7章 应力和应变分析、强度理论
7.1 应力状态概述
主平面:切应力为零的面
主应力:主平面上的正应力
任意点都可以找到三个相互垂直的主平面,因面每一点都有三个主应力
简单的拉压,三个主应力中只有一个不为零,称为单向应力状态或简单应力状态
若三个主应力中有两个不为零,称为二向平面应力状态
三个皆不为零,称为三向或空间应力状态
二向和三向称为复杂应力状态
二向和三向应力状态实例
薄壁圆筒:壁厚 δ \delta δ远小于直径D时(如 δ < D 20 \delta<\dfrac{D}{20} δ<20D)

轴向: σ ′ = p D 4 δ \sigma'=\dfrac{pD}{4\delta} σ′=4δpD
径向: σ ′ ′ = p D 2 δ \sigma''=\dfrac{pD}{2\delta} σ′′=2δpD
σ ′ \sigma' σ′与 σ ′ ′ \sigma'' σ′′皆为主应力