机器学习：非线性SVM分类器(原理+python实现)

看这篇文章的前提是已经熟知了SVM在线性可分情况下的分类原理，这篇文章的重点是在线性不可分情况下，该如何利用SVM实现分类。

一 线性不可分与SVM的目标

简单来讲，线性不可分的含义为：不能通过用一条直线或一个平面将数据集分隔开来，比如数据集是下图这样：

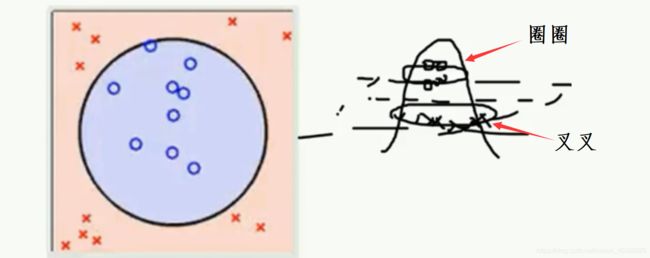
由左图可知，我们是无法利用直线来将平面上的数据点进行分类，但是将这些数据投放点到空间时，我们可以用一个平面来实现对数据点的分类。在上述分类的过程中，我们实际上对数据点进行一个"升维“的操作，将原本数据只有（x,y）二维特征上升到（x,y,z）三维特征，使得问题又转换成了线性可分的问题，那么在此条件下的SVM目标，就是找到一个能够分类数据点的平面，使得该平面距离不同类别的数据点的距离最大。
那么此时的分类函数表达式为：
优化目标为：

二 SMO算法步骤

Platt的SMO算法的步骤
步骤1：计算误差：

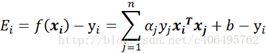
其中Xi指的是第i个数据向量，一个数据向量是由不同特征构成
Yi指的是该数据向量的类别
Ai指的是第i个数据向量所对应的alpha
注意：非线性则将xit*xj这部分换为K(Xi，Xj)，K为核函数
步骤2：计算上下界L和H：

这是相等的情况下，这里写错了
步骤3：计算η：

注意：非线性换成K(X[i],X[i]) + K(X[j],X[j]) - 2 * K(X[i],X[j])
步骤4：更新αj：

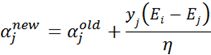
步骤5：根据取值范围修剪αj：

步骤6：更新αi：

步骤7：更新b1和b2：

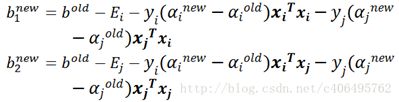
注意：非线性将b1_new中部分换为K(X[i], X[i]) 和K(X[j], X[i])
非线性将b2_new中部分换为K(X[i], X[j]) 和K(X[j], X[j])
步骤8：根据b1和b2更新b：

根据alpha求权重

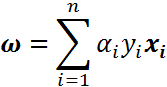
i表示第几个数据，当i=1时，即第一个数据向量
X1的数据结构为{x1,x2,x3…xn},这里的下标指的是数据向量的数据特征
那么同理，第一个数据向量的alpha1的数据结构为{a1,a2,a3…an}
所以a1y1x1的计算结果的数据结构和X1和alpha一样，均是一行
因此w的计算是将n个数据向量的w计算相加，其结构也是一行

第三部分 SMO算法实现非线性SVM

import numpy as np
import pandas as pd
# 构建线性不可分时的SVM分类器
class SVM:
    def __init__(self, max_iter=100, kernel='linear'):
        self.max_iter = max_iter
        self._kernel = kernel
        # features是m个数据样本，每个样本有n个特征，对应的类别为labels
    def init_args(self, features, labels):  # 不明白为何不在init里面设置
        # m 为样本个数 n为样本特征数
        self.m, self.n = features.shape
        self.X = features
        self.Y = labels
        self.b = 0.0
        # alpha是一个数组，大小为m*1，每个样本对应一个alpha
        self.alpha = np.ones(self.m)
        # 记录误差E的列表，大小为m*1
        self.E = [self._E(i) for i in range(self.m)]
        # 松弛变量
        self.C = 1.0
    # 判断是否满足KKT条件
    def _KKT(self, i):
        y_g = self._g(i) * self.Y[i]
        if self.alpha[i] == 0:
            return y_g >= 1
        elif 0 < self.alpha[i] < self.C:
            return y_g == 1
        else:
            return y_g <= 1
    # 计算每个样本的预测值f(Xi)
    def _g(self, i):
        r = self.b
        for j in range(self.m):
            r += self.alpha[j] * self.Y[j] * self.kernel(self.X[i], self.X[j])   #
        return r
    # 计算核函数，输入样本x1和x2就行，大小为一行多列的一维数组
    def kernel(self, x1, x2):
        if self._kernel == 'linear':
            return sum([x1[k] * x2[k] for k in range(self.n)])
        elif self._kernel == 'poly':
            return (sum([x1[k] * x2[k] for k in range(self.n)]) + 1)**2

        return 0
    # 计算误差E(xi)
    def _E(self, i):
        return self._g(i) - self.Y[i]
# 选择第一个alpha和第二个alpha的方法
    def _init_alpha(self):
        # 找出所有满足0
        index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
        # 找出不满足的，记录其索引位置
        non_satisfy_list = [i for i in range(self.m) if i not in index_list]
        index_list.extend(non_satisfy_list)
        # 对于列表里每一个
        for i in index_list:
            # 判断第i个样本的alpha是否符合kkt条件，如果符合则继续
            if self._KKT(i):
                continue
            # 计算第i个样本的误差Ei
            E1 = self.E[i]
            # 选择出Ei-Ej最大值时所对应的j
            # 如果E2是+，选择最小的；如果E2是负的，选择最大的
            if E1 >= 0:
                j = min(range(self.m), key=lambda x: self.E[x])
            else:
                j = max(range(self.m), key=lambda x: self.E[x])
            return i, j
#
    def _compare(self, alpha, L, H):
        if alpha > H:
            return H
        elif alpha < L:
            return L
        else:
            return alpha
# 完整SMO算法的主要步骤
    def fit(self, features, labels):
        self.init_args(features, labels)
        # 每一次迭代
        for t in range(self.max_iter):
            # 根据条件筛选出需要优化的第i个alpha及对应的第j个alpha
            i1, i2 = self._init_alpha()
            # 计算边界L和H
            if self.Y[i1] == self.Y[i2]:
                L = max(0, self.alpha[i1] + self.alpha[i2] - self.C)
                H = min(self.C, self.alpha[i1] + self.alpha[i2])
            else:
                L = max(0, self.alpha[i2] - self.alpha[i1])
                H = min(self.C, self.C + self.alpha[i2] - self.alpha[i1])
            # 计算i和j的误差E
            E1 = self.E[i1]
            E2 = self.E[i2]
            # 计算eta
            eta = self.kernel(self.X[i1], self.X[i1]) + self.kernel(
                self.X[i2],
                self.X[i2]) - 2 * self.kernel(self.X[i1], self.X[i2])
            if eta <= 0:
                print('eta <= 0')
                continue
            # 计算修剪的aj
            alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (
                E1 - E2) / eta
            # 计算更新后的aj
            alpha2_new = self._compare(alpha2_new_unc, L, H)
            # 计算更新后的ai
            alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (
                self.alpha[i2] - alpha2_new)
            # 计算b
            b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (
                alpha1_new - self.alpha[i1]) - self.Y[i2] * self.kernel(
                    self.X[i2],
                    self.X[i1]) * (alpha2_new - self.alpha[i2]) + self.b
            b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (
                alpha1_new - self.alpha[i1]) - self.Y[i2] * self.kernel(
                    self.X[i2],
                    self.X[i2]) * (alpha2_new - self.alpha[i2]) + self.b
            if 0 < alpha1_new < self.C:
                b_new = b1_new
            elif 0 < alpha2_new < self.C:
                b_new = b2_new
            else:
                b_new = (b1_new + b2_new) / 2
            # 将计算结果更新到之前的列表
            self.alpha[i1] = alpha1_new
            self.alpha[i2] = alpha2_new
            self.b = b_new
            self.E[i1] = self._E(i1)
            self.E[i2] = self._E(i2)
        return 'train done!'
    # 根据训练好的分类器，得到预测结果
    def predict(self, data):
        r = self.b
        # data为一个样本数据，是一行多列的一维数组，一列表示一个特征
        for i in range(self.m):
            r += self.alpha[i] * self.Y[i] * self.kernel(data, self.X[i])
        return 1 if r > 0 else -1
    # 评价预测的结果--正确率
    def score(self, X_test, y_test):
        right_count = 0
        for i in range(len(X_test)):
            result = self.predict(X_test[i])
            if result == y_test[i]:
                right_count += 1
        return right_count / len(X_test)
    # 根据alpha计算权重
    def _weight(self):
        # linear model
        yx = self.Y.reshape(-1, 1) * self.X
        self.w = np.dot(yx.T, self.alpha)
        return self.w
# 加载数据集
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = [
        'sepal length', 'sepal width', 'petal length', 'petal width', 'label'
    ]
    data = np.array(df.iloc[:100, [0, 1, -1]])
    for i in range(len(data)):
        if data[i, -1] == 0:
            data[i, -1] = -1
    return data[:, :2], data[:, -1]
X, y = create_data()
# X_train是(75,2)的二维数组 y_train是(75,)的一维数组
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
# 开始运行
svm = SVM(max_iter=100)
svm.fit(X_train, y_train)
correct_rate = svm.score(X_test, y_test)
print(correct_rate)

结果