OpenCV学习笔记(九)——直方图的操作(直方图归一化、直方图比较、直方图均衡化、直方图匹配、图像模板匹配cv.matchTemplate())
目录
- 1 直方图归一化
- 2 直方图比较
- 3 直方图均衡化
- 4 直方图匹配
- 6 图像模板匹配
直方图能够反应图像灰度值等统计特性,但是这个结果只统计了数值,是初步统计结果,OpenCV4 可以对统计结果进行进一步的操作以得到更多有用的信息,例如求取同结果的平均概率分布,通过直方图统计结果对两张图像中的内容进行不叫。本文主要介绍直方图归一化、直方图比较、直方图均衡化和直方图匹配等直方图操作与实际应用。
1 直方图归一化
由于统计的灰度图数目与图像的尺寸具有直接关系,因此如果以灰度值数目作为最终统计结果,图像经过尺寸缩放后的图像直方图会产生巨大变化。直方图可以用来表示图像的明亮程度,从理论上看,缩放前后的图像具有大志相似的直方图分布特性,因此用灰度值的数目作为统计结果具有一定的局限性。
为了减小这一局限性,可以使用用某个灰度值在所有像素中所占的比例来表示灰度值数目的多少,通过归一化可以保证每个灰度值的统计结果都在0%~100%之间。
需要注意的是,在数据类型为uint8的图像中灰度值有256种平均每个像素的灰度值所占比例为0.39%,这个比例非常小,因此为了更加直观地绘制直方图,通常需要将比例扩大一定的倍数。
还有一种常用的归一化方法是寻找统计结果种的最大数值,把所有的结果除以这个最大值,以将数据都归一化至0~1。
在OpenCV4中可以使用cv.normalize()函来实现图像的归一化处理。
#cv.normalize()函数原型
cv.normalize(src
[, dst
[, alpha
[, beta
[, norm_type
[, dtype
[, mask]]]]]])
其中各返回值和参数的含义分别为:
src:输入图像
dst:归一化结果,类型为float32,大小与输入图像相同
alpha:范围归一化时的下限
beta:范围归一化时的上限,此参数不用于标准归一化
norm_type:归一化过程种数据范数的种类标志
dtype:数据类型选择标志
mask:图像掩模
归一化过程中的数据范数的中种类标志的可选参数如下表所示。
| 标志 | 简记 | 含义 |
|---|---|---|
| cv.NORM_ INF | 1 | 无穷范数,向量的最大值 |
| cv.NORM_L1 | 2 | L1范数,绝对值之和 |
| cv.NORM_L2 | 4 | L2范数,平方和之根 |
| cv.NORM_MINMAX | 32 | 线性归一化 |
需要注意的是,无论是否归一化,或者采用哪种归一化方式,直方图的分布特性都不会改变。
示例代码
# -*- coding:utf-8 -*-
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
import sys
if __name__ == '__main__':
# 对数组进行归一化
data = np.array([2.0, 8.0, 10.0])
# 绝对值求和归一化
data_L1 = cv.normalize(data, None, 1.0, 0.0, cv.NORM_L1)
# 模长归一化
data_L2 = cv.normalize(data, None, 1.0, 0.0, cv.NORM_L2)
# 最大值归一化
data_Inf = cv.normalize(data, None, 1.0, 0.0, cv.NORM_INF)
# 偏移归一化
data_L2SQR = cv.normalize(data, None, 1.0, 0.0, cv.NORM_MINMAX)
# 展示结果
print('绝对值求和归一化结果为:\n{}'.format(data_L1))
print('模长归一化结果为:\n{}'.format(data_L2))
print('最大值归一化结果为:\n{}'.format(data_Inf))
print('偏移归一化结果为:\n{}'.format(data_L2SQR))
# 对图像直方图进行归一化
# 读取图像
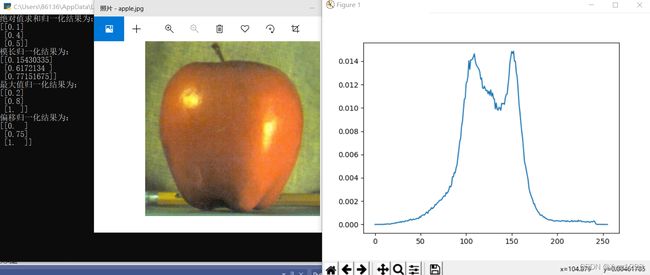
image = cv.imread('../images/apple.jpg')
# 判断图片是否读取成功
if image is None:
print('Failed to read apple.jpg.')
sys.exit()
# 将图像转为灰度图像
gray_image = cv.cvtColor(image, cv.COLOR_BGR2GRAY)
# 对图像进行直方图计算
hist_item = cv.calcHist([gray_image], [0], None, [256], [0, 256])
# 对直方图进行绝对值求和归一化
image_L1 = cv.normalize(hist_item, None, 1, 0, cv.NORM_L1)
# 对直方图进行最大值归一化
image_Inf = cv.normalize(hist_item, None, 1, 0, cv.NORM_INF)
# 展示结果
plt.plot(image_L1)
plt.show()
plt.plot(image_Inf)
plt.show()
2 直方图比较
图像的直方图表示图像灰度值的统计特性,因此可以通过比较两幅图像的直方图来看出两幅图像的相似度。**两幅图像的直方图分布相似不代表两幅图像相似,但是若两幅图像相似,则它们的直方图分布一定相似。**例如通过插值对图像进行缩放后,图像的直方图虽然不会与之前完全一致,但是两者之间一定具有很高的相似性,因此可以通过对比两幅图像的直方图分布进行对图像进行初步的筛选与识别。
在OpenCV4中可以使用cv.compareHist()函来实现图像的归一化处理。
#cv.compareHist()函数原型
retavl = cv.compareHist(H1,
H2,
method)
其中各返回值和参数的含义分别为:
retavl:两幅图像比较的结果
H1:第一幅图像的直方图
H2:第二幅图像的直方图
method:比较方法的标志
method的可选参数标志如下表所示
| 标志 | 简记 | 说明 |
|---|---|---|
| cv.HISTCMP_CORREL | 0 | 相关法 |
| cv.HISTCMP_CHISQR | 1 | 卡方法 |
| cv.HISTCMP_INTERSECT | 2 | 直方图相交法 |
| cv.HISTCMP_BHATTACHARYYA | 3 | 巴塔恰里亚距离(巴氏距离)法 |
| cv.HISTCMP_HELLINGER | 3 | 与上一标志相同 |
| cv.HISTCMP_CHISQR_ALT | 4 | 替代卡方法 |
| cv.HISTCMP_KL_DIV | 5 | 相对熵法(Kullback-Leibler散度) |
1)cv.HISTCMP_CORREL
如果两幅图像完全一致,则计算值为1;如果两幅图像的直方图完全不相关,则计算值为1。
d ( H 1 , H 2 ) = ∑ I ( H 1 ( I ) − H ˉ 1 ) ( H 2 ( I ) − H ˉ 2 ) ∑ I ( H 1 ( I ) − H ˉ 1 ) 2 ∑ I ( H 2 ( I ) − H ˉ 2 ) 2 d\left(H_{1}, H_{2}\right)=\frac{\sum_{I}\left(H_{1}(I)-\bar{H}_{1}\right)\left(H_{2}(I)-\bar{H}_{2}\right)}{\sqrt{\sum_{I}\left(H_{1}(I)-\bar{H}_{1}\right)^{2} \sum_{I}\left(H_{2}(I)-\bar{H}_{2}\right)^{2}}} d(H1,H2)=∑I(H1(I)−Hˉ1)2∑I(H2(I)−Hˉ2)2∑I(H1(I)−Hˉ1)(H2(I)−Hˉ2)
2)cv.HISTCMP_CHISQR
如果两幅图像的直方图完全一致,则计算值为0 。两幅图像的相似性越小,计算值越大。
d ( H 1 , H 2 ) = ∑ I ( H 1 ( I ) − H 2 ( I ) ) 2 H 1 ( I ) d\left(H_{1}, H_{2}\right)=\sum_{I} \frac{\left(H_{1}(I)-H_{2}(I)\right)^{2}}{H_{1}(I)} d(H1,H2)=I∑H1(I)(H1(I)−H2(I))2
3)cv.HISTCMP_INTERSECT
该方法不会将计算结果归一化,因此,两个完全一致的直方图,若来自不同图像,也会有不同的数值。两图像相比时,数值越大,表示相似性越高;数值越小,表示相似性越低。
d ( H 1 , H 2 ) = ∑ I min ( H 1 ( I ) , H 2 ( I ) ) d\left(H_{1}, H_{2}\right)=\sum_{I} \min \left(H_{1}(I), H_{2}(I)\right) d(H1,H2)=I∑min(H1(I),H2(I))
4)cv.HISTCMP_BHATTACHARYYA
若两幅图像的直方图完全一致,则计算值为0 。两幅图像的相似性越低,计算值越大。
d ( H 1 , H 2 ) = 1 − 1 H 1 H ˉ 2 N 2 ∑ I H 1 ( I ) H 2 ( I ) d\left(H_{1}, H_{2}\right)=\sqrt{1-\frac{1}{\sqrt{H_{1} \bar{H}_{2} N^{2}}} \sum_{I} \sqrt{H_{1}(I) H_{2}(I)}} d(H1,H2)=1−H1Hˉ2N21I∑H1(I)H2(I)
5)cv.HISTCMP_CHISQR_ALT
此方法判断两个直方图是否相似的方法与巴氏距离法相同,常用于替代巴氏距离法进行纹理比较。
d ( H 1 , H 2 ) = 2 ∑ I ( H 1 ( I ) − H 2 ( I ) ) 2 H 1 ( I ) + H 2 ( I ) d\left(H_{1}, H_{2}\right)=2 \sum_{I} \frac{\left(H_{1}(I)-H_{2}(I)\right)^{2}}{H_{1}(I)+H_{2}(I)} d(H1,H2)=2I∑H1(I)+H2(I)(H1(I)−H2(I))2
6)cv.HISTCMP_KL_DIV
如果两幅图像的直方图完全一致,则计算值为0 。两幅图像的相似度越低,则计算值越大。
d ( H 1 , H 2 ) = ∑ I H 1 ( I ) ln ( H 1 ( I ) H 2 ( I ) ) d\left(H_{1}, H_{2}\right)=\sum_{I} H_{1}(I) \ln \left(\frac{H_{1}(I)}{H_{2}(I)}\right) d(H1,H2)=I∑H1(I)ln(H2(I)H1(I))
示例代码
# -*- coding:utf-8 -*-
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
import sys
def normalize_image(path):
# 以灰度方式读取图像
image = cv.imread(path, 0)
# 判断图片是否读取成功
if image is None:
print('Failed to read image.')
sys.exit()
# 绘制直方图(可省略)
plt.hist(image.ravel(), 256, [0, 256])
plt.title(path.split('/')[-1])
plt.show()
# 计算图像直方图
image_hist = cv.calcHist([image], [0], None, [256], [0, 256])
# 进行归一化
normalize_result = np.zeros(image_hist.shape, dtype=np.float32)
cv.normalize(image_hist, dst=normalize_result, alpha=0, beta=1.0, norm_type=cv.NORM_MINMAX)
return normalize_result
def compare_hist(image1_path, image2_path):
image1 = normalize_image(image1_path)
image2 = normalize_image(image2_path)
# 进行图像直方图比较
return round(cv.compareHist(image1, image2, method=cv.HISTCMP_CORREL), 2)
if __name__ == '__main__':
img1_path = '../images/Compare_Hist_1.jpg'
img2_path = '../images/Compare_Hist_2.jpg'
img3_path = '../images/Compare_Hist_3.jpg'
img4_path = '../images/Compare_Hist_4.jpg'
print('Compare_Hist_1.jpg与Compare_Hist_2.jpg的相似性为:%s' % (compare_hist(img1_path, img2_path)))
print('Compare_Hist_3.jpg与Compare_Hist_4.jpg的相似性为:%s' % (compare_hist(img3_path, img4_path)))
3 直方图均衡化
如果一幅图像的直方图都集中在一个区域,则整体图像的对比度较小,不变于图像中的纹理识别。如果所有像素的灰度值分布较集中,则整个图像将会给人一种模糊的感觉。如果通过映射关系将图像中灰度值的范围扩大,增加原来两个灰度值之间的差距,就可以提高图像的对比度,进而将图像中的灰度值之间的插值,就可以提高图像的对比度,进而将图像中的纹理突出显现出来,这个过程称为图像直方图均衡化。
在OpenCV4中可以使用cv.equalizeHist()函来实现直方图均衡化。
#cv.equalizeHist()函数原型
cv.equalizeHist(src
[, dst])
其中各返回值和参数的含义分别为:
src:需要直方图均衡化的8位单通道图像
dst:直方图均衡化的输出图像,与src具有相同的尺寸和数据类型。
需要注意的是,该函数只能对单通道的灰度图进行 直方图均衡化。
经过均衡化后,图像的对比度会明显增加,图像的直方图分布会更加均匀。
示例代码
# -*- coding:utf-8 -*-
import cv2 as cv
from matplotlib import pyplot as plt
import sys
if __name__ == '__main__':
# 读取图像
image = cv.imread('../images/equalizeHist.jpg', 0)
# 判断图片是否读取成功
if image is None:
print('Failed to read equalizeHist.jpg.')
sys.exit()
# 绘制原图直方图
plt.hist(image.ravel(), 256, [0, 256])
plt.title('Origin Image')
plt.show()
# 进行均衡化并绘制直方图
image_result = cv.equalizeHist(image)
plt.hist(image_result.ravel(), 256, [0, 256])
plt.title('Equalized Image')
plt.show()
# 展示均衡化前后的图片
cv.imshow('Origin Image', image)
cv.imshow('Equalized Image', image_result)
cv.waitKey(0)
cv.destroyAllWindows()
4 直方图匹配
cv.equalizeHist()函数可以自动改变直方图的分布形式,这种方式极大地简化了直方图均衡化过程中的操作步骤,但是该函数不能指定均衡化后的直方图分布形式。在某些特定的条件下,需要将直方图映射成指定的分布形式,这种将直方图映射成指定分布形式的算法称为直方图匹配或者直方图规定化。直方图匹配与直方图均衡化相似,都改变图像的直方图分布形式,只是直方图均衡化后图像的直方图是均匀分布的,而直方图匹配后直方图可以随意指定,即在执行直方图匹配操作时首先要知道变换后的灰度直方图分布形式,进而确定变换函数。直方图匹配操作能够有目的地增强某个灰度区间。相比于直方图均衡化操作,该算法虽然多了一个输入,但是其变换后的结果更灵活。
由于不同图像的像素数目可能不同,因此为了使两幅图像的直方图能够匹配,需要使用概率的形式表示每个灰度值在图像像素中所占的比例。理想状态下,在经过直方图匹配操作后,直方图的分布形式应与目标分布致,因此两者之间的累积概率分布也一致。累积概率为小于或等于某一灰度值的像素数目占所有像素数的比例。我们用 V s V_s Vs表示原图像的直方图中各个灰度级的累积概率,用表示直方图匹配后直方图中各个灰度级的累积概率。
直方图匹配示例如下图所示。

这个寻找灰度值匹配的过程是直方图匹配算法的关键。在代码实现中,我们可以通过构建原直方图累积概率与目标直方图累积概率之间的差值表,寻找原直方图中灰度值n的累积概率与目标直方图中所有灰度值累积概率差值的最小值,这个最小值对应的灰度值r就是n匹配后的灰度值。
OpenCV4 中没有提提供直方图匹配的函数,所有需要自己根据代码实现直方图匹配。
示例代码
# -*- coding:utf-8 -*-
import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
import sys
if __name__ == '__main__':
# 读取图像
image1 = cv.imread('../images/Hist_Match.png')
image2 = cv.imread('../images/equalLena.png')
# 判断图片是否读取成功
if image1 is None or image2 is None:
print('Failed to read Hist_Match.png or equalLena.png.')
sys.exit()
# 计算两张图像的直方图
hist_image1 = cv.calcHist([image1], [0], None, [256], [0, 256])
hist_image2 = cv.calcHist([image2], [0], None, [256], [0, 256])
# 对直方图进行归一化
hist_image1 = cv.normalize(hist_image1, None, norm_type=cv.NORM_L1)
hist_image2 = cv.normalize(hist_image2, None, norm_type=cv.NORM_L1)
# 计算两张图像直方图的累计概率
hist1_cdf = np.zeros((256, ))
hist2_cdf = np.zeros((256, ))
hist1_cdf[0] = 0
hist2_cdf[0] = 0
for i in range(1, 256):
hist1_cdf[i] = hist1_cdf[i - 1] + hist_image1[i]
hist2_cdf[i] = hist2_cdf[i - 1] + hist_image2[i]
# 构建累计概率误差矩阵
diff_cdf = np.zeros((256, 256))
for k in range(256):
for j in range(256):
diff_cdf[k][j] = np.fabs((hist1_cdf[k] - hist2_cdf[j]))
# 生成LUT映射表
lut = np.zeros((256, ), dtype='uint8')
for m in range(256):
# 查找源灰度级为i的映射灰度和i的累计概率差值最小的规定化灰度
min_val = diff_cdf[m][0]
index = 0
for n in range(256):
if min_val > diff_cdf[m][n]:
min_val = diff_cdf[m][n]
index = n
lut[m] = index
result = cv.LUT(image1, lut)
# 展示结果
cv.imshow('Origin Image1', image1)
cv.imshow('Origin Image2', image2)
cv.imshow('Result', result)
_, _, _ = plt.hist(x=image1.ravel(), bins=256, range=[0, 256])
plt.show()
_, _, _ = plt.hist(x=image2.ravel(), bins=256, range=[0, 256])
plt.show()
_, _, _ = plt.hist(x=result.ravel(), bins=256, range=[0, 256])
plt.show()
cv.waitKey(0)
cv.destroyAllWindows()
6 图像模板匹配
我们在图像中寻找模板图像时,可以之间通过比较图像像素的形式来搜索是否存在相同的内容。模板匹配通常用于在一幅图像中寻找特定内容。由于模板图像的尺寸小于待匹配图像的尺寸,同时又需要比较两幅图像中每一个像素的灰度值,因此常在待匹配图像中选择与模板尺寸相同的滑动窗口。通过比较滑动窗口与模板的相似程度,就可以判断匹配图像中是否含有与模板图像相同的内容。
模板匹配的示意图如下图所示。

模板匹配的过程如下:
(1)在待匹配图像中选取与模板图像尺寸相同的滑动窗口。
(2)比较滑动窗口中每个像素的灰度值与模板中对应像素灰度值的关系,计算模板与滑动窗口的相似性。
(3)将滑动窗口从左上角开始向右滑动,滑动到最右边后向下滑动一行,然后从最左侧重新开始滑动。记录每一次移动后计算得到模板与滑动窗口的相似性。
(4)比较所有位置的相似性,选择相似性最大的滑动窗口作为备选匹配结果。
在OpenCV4中可以使用cv.matchTemplate()函来实现模板匹配过程中图像与模板相似性的计算。该函数可进行字母、数字等简单字符的匹配。
#cv.matchTemplate()函数原型
result = cv.matchTemplate(image,
templ,
method
[, result
[, mask]])
其中各返回值和参数的含义分别为:
image:待匹配模板的原图像
templ:模板图像
method:模板匹配方法的标志
result:模板匹配结果图像
mask:匹配模板的掩模
灰度图像和彩色图像都可以使用该函数进行模板匹配,但是输入图像的数据类型需要为 uint8 或 float32中的一种,匹配结果通过值进行返回。
模板匹配方法 method 的可选标志如下表所示。
| 标志 | 简记 | 说明 |
|---|---|---|
| cv.TM_SQDIFF | 0 | 平方差匹配法 |
| cv.TM_SQDIFF_NORMED | 1 | 归一化平方差匹配法 |
| cv.TM_CCORR | 2 | 相关匹配法 |
| cv.TM_CCORR_NORMED | 3 | 归一化相关匹配法 |
| cv.TM_CCOEFF | 4 | 系数匹配法 |
| cv.TM_CCOEFF_NORMED | 5 | 归一化相关系数匹配法 |
1)TM_SQDIFF
平方差匹配法利用平方差进行匹配,当模板与滑动窗口完全匹配时,计算值为0。两者的匹配度月底,计算值越大。
R ( x , y ) = ∑ x ′ , y ′ ( T ( x ′ , y ′ ) − I ( x + x ′ , y + y ′ ) ) 2 R(x, y)=\sum_{x^{\prime},y^{\prime}}\left(T\left(x^{\prime}, y^{\prime}\right)-I\left(x+x^{\prime}, y+y^{\prime}\right)\right)^{2} R(x,y)=x′,y′∑(T(x′,y′)−I(x+x′,y+y′))2
2)TM_SQDIFF_NORMED
归一化平方差匹配法,将平方差匹配法进行归一化,使输入结果归一化到0~1,当模板与滑动窗口完全匹配时,计算值为0。两者的匹配度月底,计算值越大。
R ( x , y ) = ∑ x ′ , y ′ ( T ( x ′ , y ′ ) − I ( x + x ′ , y + y ′ ) ) 2 ∑ x ′ , y ′ T ( x ′ , y ′ ) 2 ∑ x ′ , y ′ I ( x + x ′ , y + y ′ ) 2 R(x, y)=\frac{\sum_{x^{\prime}, y^{\prime}}\left(T\left(x^{\prime}, y^{\prime}\right)-I\left(x+x^{\prime}, y+y^{\prime}\right)\right)^{2}}{\sqrt{\sum_{x^{\prime}, y^{\prime}} T\left(x^{\prime}, y^{\prime}\right)^{2} \sum_{x^{\prime}, y^{\prime}} I\left(x+x^{\prime}, y+y^{\prime}\right)^{2}}} R(x,y)=∑x′,y′T(x′,y′)2∑x′,y′I(x+x′,y+y′)2∑x′,y′(T(x′,y′)−I(x+x′,y+y′))2
3)TM_CCORR
相关匹配法采用模板和图像间的乘法操作,数值越大,匹配效果越好,0表示最坏的匹配结果。
R ( x , y ) = ∑ x ′ , y ′ ( T ( x ′ , y ′ ) I ( x + x ′ , y + y ′ ) ) R(x, y)=\sum_{x^{\prime}, y^{\prime}}\left(T\left(x^{\prime}, y^{\prime}\right) I\left(x+x^{\prime}, y+y^{\prime}\right)\right) R(x,y)=x′,y′∑(T(x′,y′)I(x+x′,y+y′))
4)TM_CCORR_NORMED
归一化相关匹配法将相关匹配法进行归一化,使输入结果归一化到0~1,当模板与滑动窗口完全匹配时,计算值为1;当两者完全不匹配时,计算值为0。
5)TM_CCOEFF
系数匹配法采用相关匹配法对模板减去均值的结果和原图像减去均值的结果进行匹配。**这种方法可以很好地解决模板图像和原图像之间由于亮度不同而产生的影响。**模板与滑动窗口匹配度越高,计算值越大;匹配度越低,计算值越小。该方法的计算结果可能为负数。
R ( x , y ) = ∑ x ′ y ′ ( T ′ ( x ′ , y ′ ) I ′ ( x + x ′ , y + y ′ ) ) R(x, y)=\sum_{x^{\prime} y^{\prime}}\left(T^{\prime}\left(x^{\prime}, y^{\prime}\right) I^{\prime}\left(x+x^{\prime}, y+y^{\prime}\right)\right) R(x,y)=x′y′∑(T′(x′,y′)I′(x+x′,y+y′))
其中
T ′ ( x ′ , y ′ ) = T ( x ′ , y ′ ) − 1 w h ∑ x ′ , y ′ T ( x ′ ′ , y ′ ′ ) I ′ ( x + x ′ , y + y ′ ) = I ( x + x ′ , y + y ′ ) − 1 w h ∑ x ′ ′ , y ′ ′ I ( x + x ′ ′ , y + y ′ ′ ) \begin{gathered} T^{\prime}\left(x^{\prime}, y^{\prime}\right)=T\left(x^{\prime}, y^{\prime}\right)-\frac{1}{w h} \sum_{x^{\prime}, y^{\prime}} T\left(x^{\prime \prime}, y^{\prime \prime}\right) \\ I^{\prime}\left(x+x^{\prime}, y+y^{\prime}\right)=I\left(x+x^{\prime}, y+y^{\prime}\right)-\frac{1}{w h} \sum_{x^{\prime \prime}, y^{\prime \prime}} I\left(x+x^{\prime \prime}, y+y^{\prime \prime}\right) \end{gathered} T′(x′,y′)=T(x′,y′)−wh1x′,y′∑T(x′′,y′′)I′(x+x′,y+y′)=I(x+x′,y+y′)−wh1x′′,y′′∑I(x+x′′,y+y′′)
6)TM_CCOEFF_NORMED
归一化相关系数匹配法,将系数匹配法进行归一化,使得输入结果归一化到-1~1 。当模板与滑动窗口完全匹配时,计算值为1;当两者完全不匹配时,计算值为-1。
R ( x , y ) = ∑ x ′ , y ′ ( T ′ ( x ′ , y ′ ) I ′ ( x + x ′ , y + y ′ ) ) ∑ x ′ , y ′ T ( x ′ , y ′ ) 2 ∑ x ′ , y ′ I ′ ( x + x ′ , y + y ′ ) 2 R(x, y)=\frac{\sum_{x^{\prime}, y^{\prime}}\left(T^{\prime}\left(x^{\prime}, y^{\prime}\right) I^{\prime}\left(x+x^{\prime}, y+y^{\prime}\right)\right)}{\sqrt{\sum_{x^{\prime}, y^{\prime}} T\left(x^{\prime}, y^{\prime}\right)^{2} \sum_{x^{\prime}, y^{\prime}} I^{\prime}\left(x+x^{\prime}, y+y^{\prime}\right)^{2}}} R(x,y)=∑x′,y′T(x′,y′)2∑x′,y′I′(x+x′,y+y′)2∑x′,y′(T′(x′,y′)I′(x+x′,y+y′))
了解了不同的计算相似性方法后,我们重点需要知道在 每种方法中最佳匹配结果的数值应该是较大值还是较小值。由于cv.matchTemplate()函数的输出结果是有相关性系数的矩阵,因此需要通过 cv.minMaxLoc() 函数寻找输入矩阵中的最大值或者最小值,讲而确定模板匹配的结果。
示例代码
# -*- coding:utf-8 -*-
import cv2 as cv
import sys
if __name__ == '__main__':
# 读取图像并判断是否读取成功
image = cv.imread('../images/matchTemplate.jpg')
template = cv.imread('../images/match_template.jpg')
if image is None or template is None:
print('Failed to read matchTemplate.jpg or match_template.jpg.')
sys.exit()
cv.imshow('image', image)
cv.imshow('template', template)
# 计算模板图片的高和宽
h, w = template.shape[:2]
# 进行图像模式匹配
result = cv.matchTemplate(image, template, method=cv.TM_CCOEFF_NORMED)
min_val, max_val, min_loc, max_loc = cv.minMaxLoc(result)
# 计算图像左上角、右下角坐标并画出匹配位置
left_top = max_loc
right_bottom = (left_top[0] + w, left_top[1] + h)
cv.rectangle(image, left_top, right_bottom, 255, 2)
cv.imshow('result', image)
cv.waitKey(0)
cv.destroyAllWindows()
下一篇将会介绍OpenCV中与图像卷积有关的内容。