阵列信号处理仿真之四——Z变换分析阵列多项式
利益Z变换分析阵列多项式的零点分布
- Z变换
- 实数阵列权值
- 案例
-
- 均匀加权阵列
-
- matlab代码
- cosine,cosine平方
-
- matlab代码
- Hamming,Blackman-Harris
-
- matlab代码
Z变换
对于线性等间距阵列,波束方向图可以用一个阵列多项式来表示。波束方向图在 ψ \psi ψ空间可以写成 B ψ ( ψ ) = e − j ( N − 1 2 ) ψ ( ∑ n = 0 N − 1 ω n e − j n ψ ) B_\psi(\psi)=e^{-j(\frac{N-1}{2})\psi}(\sum_{n=0}^{N-1}\omega_ne^{-jn\psi}) Bψ(ψ)=e−j(2N−1)ψ(n=0∑N−1ωne−jnψ)
我们定义 z = e j ψ z=e^{j\psi} z=ejψ
则可以写出 B z ( z ) = ∑ n = 0 N − 1 ω n z − n B_z(z)=\sum_{n=0}^{N-1}\omega_nz^{-n} Bz(z)=n=0∑N−1ωnz−n
这个表达式和z变换相似,把实变量 ψ \psi ψ映射到一个具有单位幅度的复变量z,变量 ψ \psi ψ是复变量z的相位。波束方向图可以写成 B ψ ( ψ ) = [ z − N − 1 2 B z ( z ) ] z = e j ψ B_\psi(\psi)=[z^{-\frac{N-1}{2}}B_z(z)]_{z=e^{j\psi}} Bψ(ψ)=[z−2N−1Bz(z)]z=ejψ
实数阵列权值
对于对称加权,有 ω ( n ) = ω ( N − 1 − n ) \omega(n)=\omega(N-1-n) ω(n)=ω(N−1−n)
z变换为 B z ( z ) = ∑ n = 0 N − 1 ω ( n ) z − n B_z(z)=\sum_{n=0}^{N-1}\omega(n)z^{-n} Bz(z)=n=0∑N−1ω(n)z−n
可以定义 M = N − 1 2 M=\frac{N-1}{2} M=2N−1
并写出 B z ( z ) = z − M { ω ( M ) + ω ( M − 1 ) [ z + z − 1 ] + ω ( M − 2 ) [ z 2 + z − 2 ] + ⋯ + ω ( 0 ) [ z M + z − M ] } Bz(z)=z^{-M}\{\omega(M)+\omega(M-1)[z+z^{-1}]+\omega(M-2)[z^2+z^{-2}]+\cdots +\omega(0)[z^M+z^{-M}]\} Bz(z)=z−M{ω(M)+ω(M−1)[z+z−1]+ω(M−2)[z2+z−2]+⋯+ω(0)[zM+z−M]}
根据系数的对称性 B z ( z − 1 ) = z 2 M B z ( z ) B_z(z^{-1})=z^{2M}B_z(z) Bz(z−1)=z2MBz(z)
这里不再继续往后推导,经过分析,最终我们可以推出,多项式零点四个为一组,互为共轭和互为倒数的零点对,下面我们将分析一些实际的案例
案例
均匀加权阵列
B u ( u ) = 1 N s i n ( π N d λ u ) s i n ( π d λ u ) , − 1 ≤ u ≤ 1 B_u(u)=\frac{1}{N}\frac{sin(\frac{\pi N d}{\lambda}u)}{sin(\frac{\pi d}{\lambda}u)},-1\leq u \leq 1 Bu(u)=N1sin(λπdu)sin(λπNdu),−1≤u≤1
方向图的阵列出现在 B u ( u ) B_u(u) Bu(u)的分子为0而分母不为0时 s i n ( π N d λ u ) = 0 sin(\frac{\pi Nd}{\lambda}u)=0 sin(λπNdu)=0
零点的位置为 u n = ± n N ⋅ λ d , n = 1 , 2 , ⋯ , N − 1 2 u_n = \pm\frac{n}{N}\cdot\frac{\lambda}{d},n=1,2,\cdots,\frac{N-1}{2} un=±Nn⋅dλ,n=1,2,⋯,2N−1
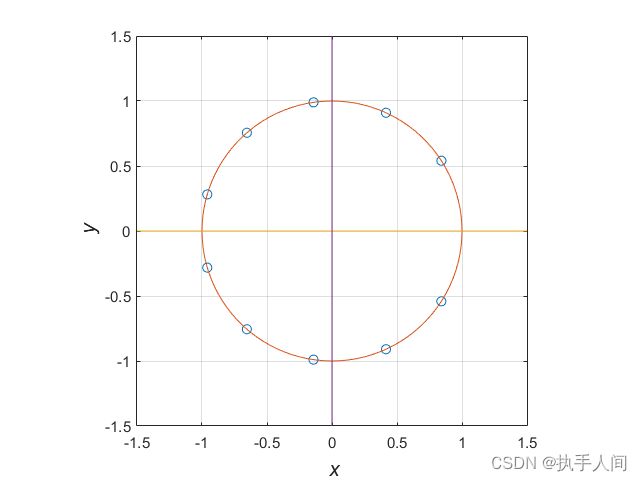
我们记得第一零点的位置决定了主波束的宽度.所以,我们可以研究这样的技术,即约束第一个零点在一个特定点上,并调整其他零点的位置以得到一个理想的方向图形状。很多经常使用的方向图都是以这种方式开发出来的。
matlab代码
clear all;
close all;
N = 11;
theta=2*pi*[0:0.01:1];
w = 1/N*ones(N,1);
z = roots(w);
figure
plot(real(z),imag(z),'o');
hold on;
plot(cos(theta),sin(theta),'-');
plot(1.5*[-1,1],0*[1,1],'-')
plot(0*[1,1],1.5*[-1,1],'-')
hold off;
set(gca,'YTick',[-1.5 -1 -0.5 0 0.5 1 1.5])
axis square
grid on;
xlabel('{\it x}','Fontsize',14)
ylabel('\it y','Fontsize',14)
cosine,cosine平方

这两个零点图对应的波束方向图上篇文章中已经讲过这里不再多提。
matlab代码
clear all
close all
N=11;
n=conj(-(N-1)/2:(N-1)/2)';
w2=cos(pi*n/N);
w3=w2.*w2;
z2=roots(w2);
z3=roots(w3);
% ---------------- Zero Plot.
figure
%%%%%%%%%%%% plot 1
subplot(1,2,1);
plot(real(z2),imag(z2),'o');
axis([-1.2 1.2 -1.2 1.2])
axis('square')
grid on;
title('Cosine','Fontsize',14);
xlabel('Real','Fontsize',14)
ylabel('Imaginary','Fontsize',14)
theta=2*pi*[0:0.01:1];
hold on
plot(cos(theta),sin(theta),'--');
plot([-0.9 -0.65],[0.03 0.17])
text(-0.6,0.2,'2 zeros','Fontsize',12)
hold off
%%%%%%%%%%% plot 2
subplot(1,2,2);
plot(real(z3),imag(z3),'o');
grid on;
axis([-1.2 1.2 -1.2 1.2])
axis('square')
title('Cosine-squared','Fontsize',14);
xlabel('Real','Fontsize',14)
ylabel('Imaginary','Fontsize',14)
theta=2*pi*[0:0.01:1];
hold on
plot(cos(theta),sin(theta),'--');
text(-1.2,-1.7,(['Another zero is at (',num2str(real(z3(1))),', ',num2str(imag(z3(1))),')']),'Fontsize',12)
%text(1.6,-0.5,(['another zero at :']));
%text(1.7,-1,(['( ',num2str(real(z3(1))),' , ',num2str(imag(z3(1))),' )']))
hold off
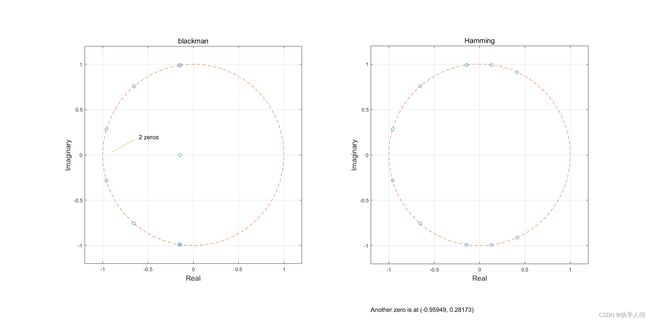
Hamming,Blackman-Harris
Hamming窗权值 ω ( n ) = 0.54 + 0.46 c o s ( 2 π n ~ N ) \omega(n) = 0.54+0.46cos(\frac{2\pi \tilde n}{N}) ω(n)=0.54+0.46cos(N2πn~)
Blackman-Harris权值 ω ( n ) = 0.42 + 0.5 c o s ( 2 π n ~ N ) + 0.08 c o s ( 4 π n ~ N ) \omega(n) = 0.42+0.5cos(\frac{2\pi \tilde n}{N})+0.08cos(\frac{4\pi \tilde n}{N}) ω(n)=0.42+0.5cos(N2πn~)+0.08cos(N4πn~)
matlab代码
N=11;
n=conj(-(N-1)/2:(N-1)/2)';
w2=0.42+0.5*cos(2*pi*n/N)+0.08*cos(4*pi*n/N);
w3=0.54+0.46*cos(2*pi*n/N);
z2=roots(w2);
z3=roots(w3);
% ---------------- Zero Plot.
figure
%%%%%%%%%%%% plot 1
subplot(1,2,1);
plot(real(z2),imag(z2),'o');
axis([-1.2 1.2 -1.2 1.2])
axis('square')
grid on;
title('blackman','Fontsize',14);
xlabel('Real','Fontsize',14)
ylabel('Imaginary','Fontsize',14)
theta=2*pi*[0:0.01:1];
hold on
plot(cos(theta),sin(theta),'--');
plot([-0.9 -0.65],[0.03 0.17])
text(-0.6,0.2,'2 zeros','Fontsize',12)
hold off
%%%%%%%%%%% plot 2
subplot(1,2,2);
plot(real(z3),imag(z3),'o');
grid on;
axis([-1.2 1.2 -1.2 1.2])
axis('square')
title('Hamming','Fontsize',14);
xlabel('Real','Fontsize',14)
ylabel('Imaginary','Fontsize',14)
theta=2*pi*[0:0.01:1];
hold on
plot(cos(theta),sin(theta),'--');
text(-1.2,-1.7,(['Another zero is at (',num2str(real(z3(1))),', ',num2str(imag(z3(1))),')']),'Fontsize',12)
%text(1.6,-0.5,(['another zero at :']));
%text(1.7,-1,(['( ',num2str(real(z3(1))),' , ',num2str(imag(z3(1))),' )']))
hold off